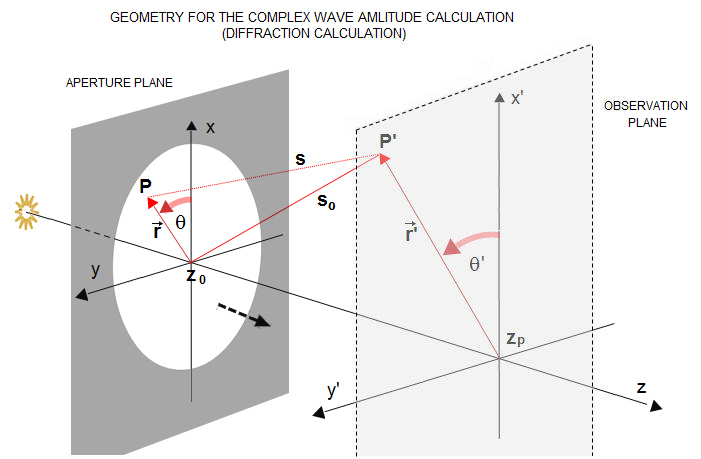
|
telescopeѲptics.net ▪ ▪ ▪ ▪ ▪▪▪▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ CONTENTS 1. TELESCOPE IMAGE: RAYS, WAVEFRONTS AND DIFFRACTIONPAGE HIGHLIGHTS By making space objects brighter and larger visually, telescopes greatly expand our ability of their detection and observation. But how do they do it? What influences their performance, and how? This is the subject of this text. There are two main aspects to how telescopes form images of planets, stars and galaxies. One is concerned with the physics of image formation and the other with its geometry. We need the former to determine how light waves behave in the telescope, or optical system in general: where do they go, and how their interactions determine image brightness, contrast and resolution. The latter is a linear interface based on the simplified directional model of light propagation. The former is physical optics, and the latter geometrical optics. First-order geometrical optics (also: paraxial, or Gaussian approximation) provides convenient way of determining image location and magnification by tracking paraxial rays. Tracking rays that pass through optical systems at larger angles require more complex calculation, but it is unavoidable for determining image aberrations, either geometric, or phase (physical optics, diffraction) aberrations resulting from the differences in optical path lengths for different rays at the focus location. Rays, waves and wavefront Any optical image - and those formed by telescopes are no exception - is made of light: a form of electro-magnetic radiation. More precisely, telescope image is made by imaging a countless number of light-emitting point-sources from faraway objects. As shown on FIG. 1, light waves emitted by a point-source spread out in a concentric pattern, propagating as an oscillating energy field. It is convenient to present wave oscillation as a cycle, the full cycle being 360 degrees, or 2π radians. Phase of wave oscillation is, for harmonic sinusoidal wave, defined by o=Asin(2πx/λ), where A is the wave amplitude, defined as the maximum value of wave oscillation, x is the length of wave path from the origin, and λ the wavelength of light (FIG. 1, top left). An imaginary surface connecting wave points of identical oscillatory motion, or phase, is called phasefront. Geometrical approximation of the phasefront, based on the identical ray optical path length (OPL) from the source is called optical wavefront, or simply wavefront. For optical telescopes, phasefront and wavefront are, for all practical purposes, identical as long as the wavefront error remains relatively small. The difference between the two comes from the latter increasing directly with the nominal wavefront deviation, while the former effectively oscillates from the maximum constructive interference for wavefront points deviating any whole number of waves - including, of course, zero deviation - decreasing to zero constructive interference from any wavefront point deviating by an odd whole number of half-wave deviations. Ray, on the other hand, is simply a straight line with the origin at the point-source, that remains perpendicular to the wavefront. While rays are useful in presenting geometrical aspects of optical phenomena, they represent only a tiny fraction of the total energy propagating through the energy field. Furthermore, it is only their geometric properties that are being considered. Therefore, ray (or geometric) optics has no direct relation with physical properties of the energy field.
Geometry of rays is superficial, but useful concept, not only for approximating image location and size, but for the initial assessment of its quality as well. Since any wavefront deformation causes ray disturbance, scattering them around the center of curvature of a perfect reference spherical wavefront, it indicates whether an optical system is perfect, or not. To some extent, ray disturbance indicates the severity of wavefront error, which makes it a convenient tool for the initial assessment of wavefront/image quality. Also, it is useful for determining geometric relations between optical elements and images they form. However, for the specifics about actual energy distribution around the focal point we need physical optics. The wavefront, while itself a geometric category, is more directly related to the underlying physics. It identifies the location of in-phase wave sources, making it the basis for calculations determining the properties of wave interactions at and around focal point - i.e. diffraction calculation. Hence, the significance of the wavefront is in that its form directly determines the quality of optical imaging in a telescope. Obviously, form of the wavefront and geometric properties of the rays are directly inter-related, but the ray geometry remains only loosely related to the interactions taking place within the energy field. The most striking example is that of a spherical wavefront, whose rays all meet in a single point. At the same time, the actual physical image formed by waves emerging from the wavefront is a bright spot surrounded by a series of fading rings. How is this taking place? The answer is that light energy does not propagate in straight lines; rather, it propagates according to the Huygens's principle. But first a quick look at how light waves interfere. Wave interference, combined intensity Whenever energy fields emitted by two or more light sources fill the same space, they will interfere. Or, put plainly, depending or how close in phase are their respective wave oscillations at the specific point in space, they will combine either constructively, producing more energy, or destructively, producing less, or none. As illustration below shows, the closer in phase are interfering waves, the more constructive interference, and vice versa. If no other wave sources would be present, this would be the interference pattern of these two energy fields. If the two emitters were singled out by a dual aperture, with about three wavelengths of separation - their interfering fields spreading out would be conventionally called diffracted field. In the observational plane at some distance, it would project a pattern of bright and dark lines - maximas and minimas, respectively, with the former formed by a continuous deposition of energy peaks. The maximas are called diffraction orders: from zero order in the center, toward subsequent orders marked with positive integers for maximas above the central, and negative integers for those below. The illustration shows interference of phase with the constant phase relationship, i.e. coherent light (which, as in the Young's experiment, can be obtained by splitting the field from a single monochromatic point source by a pair of small openings). With incoherent light, i.e. with the phase relationship randomly changing countless number of times each second, wave interference and diffraction orders are also randomly spread round, resulting in a much less contrasty - or undetectable - interference/diffraction pattern. This is reflected in the basic formalism of wave interference. With the wave energy - or intensity - I defined as the wave amplitude A squared, i.e. I=A2 (general form), the combined intensity of two waves is their combined amplitude squared, or IC=(A1+A2)2. Hence, the maximum combined intensity for two separated wave sources of intensities I1 and I2 can be written as IC = I1 + I2 + 2A1A2 cos(ΔΦ)ɤ, with ɤ, the complex degree of coherence, ranging from 0 for incoherent to 1 for fully coherent light. The third term at right is so called interference term, which vanishes in incoherent light (ɤ=0) so that the combined intensity is simply a sum of the two intensities, ICi=I1+I2. With partly coherent light, value of the interference term varies with both, phase difference ΔΦ and ɤ, while for fully coherent light (ɤ=1) it varies with phase difference; for two waves in phase, i.e. ΔΦ=0 or ΔΦ=2π, cos(ΔΦ)=1 and the combined intensity is at its maximum, ICcmax=I1+I2+2A1A2. For A1=A2=A0, and A02=I0, the combined intensity is ICcmax=4I0, as opposed to ICi=2I0 with incoherent light and A1=A2=A0. With the maximum combined intensity for incoherent light normalized to 1, the combined intensity of two point sources in the pupil, as a function of OPD, in units of wavelength, is given by:
which for OPD=λ/2 gives I=cos2(π/2)=0. The wider emitter separation, the smaller field angle at which λ/2 OPD is generated and the combined intensity drops to zero. For two wavefront point-emitters at the opposite ends of 100mm diameter pupil (S=182,000λ for λ=0.00055mm), this mutual cancellation will take place at the field angle α=0.57 arc seconds. The combined amplitude of two interfering waves is given by AC=cos(OPDπ/λ), with (OPDπ/λ)=ΔΦ being the phase difference. It can be presented as the resultant vector of two unit phase vectors, as illustrated on Inset C. Since the OPD between waves w1 and w2 is λ/4, their combined amplitude is AC=cos(π/4)=√0.5; the resulting combined intensity is I1+2=AC2=0.5, as obtained by applying Eq. (b) directly. Likewise, for waves w1 and w3, the phase difference is 1.25π, giving OPD=1.25/2=0.625, with the resulting amplitude given by cos(0.625π)=-0.3827, and the combined intensity I1+3=cos2(0.625π)=0.1464. From Eq. (b), the phase differential in terms of combined normalized intensity is given by ∆Φ=2cos-1√I, and the corresponding field angle sine is sinα=(cos-1√I)λ/πS (cos-1 is the inverse cosine function, i.e. the angle corresponding to a given cosine value). The intensity plot for λ/2 point separation (Inset D, left) shows that the normalized intensity I of two combined waves drops to 0.5 at the phase difference of ∆Φ=π/2 (α=30°), and that there is little of constructive interference taking place for phase difference ∆Φ>π/1.31 (α>60°). Intensity drops to zero for α=90° and α=270°, since the two emitters are effectively located on the horizontal axis, centered around zero point and separated by S=λ/2. A plot showing dependence of combined intensity on the angular radius α in the image plane retains this form as long as the S/(λ/2) quotient is a whole number, but the angular radius within which most of constructive interference takes place diminishes. As the point separation increases, the central lobe becomes smaller angularly; within those same coordinates, the plot for S=1000λ separation - which is still only 0.55mm for λ=0.00055mm - would be practically a straight vertical line, but with a number of radially distributed subsidiary maximas whenever the net OPD difference reaches a whole number of waves (for S giving integer when divided with other values than λ/2 the combined intensity at 90° and 270° is non-zero, and it forms full maxima when S consists of a whole number of waves). Of course, energy generated at every point of the image is a sum of wave contributions not only from a pair of wave emitters, but from all wave emitters combined. The complexity of wave interactions is beyond visualization; an attempt at illustration shows the change in oscillation (phase) along the image radius for four pairs of emitters of different inter-separations (Inset A, bottom). A slightly separated pair (1) gives maximum contribution to all field points within the radius shown. Contribution of somewhat less closely positioned pair (2) decreases more rapidly with the increase in field radius, and much more rapidly for more widely separated (3) and the widest (4) pair. As can be seen on the plot for the pair 4, contribution from every pair varies periodically between the maximum and zero, as a function of the field angle (radius). At the field point A, the two more widely separated pairs' phase contribution is zero, but the combined contribution of narrowly separated pairs of emitters (1 and 2) is still close to a maximum; at double the field radius, the two more widely separated pairs' contribution will be at the maximum, but it will be lower for the pair 2. Interference of light between principal and diffracted waves is what determines physical properties of the image formed by a telescope.
|
A 2-dimensional EM wave is usually presented as a continuous series of subsequent oscillations of electric and magnetic field, each oscillating in its plane, perpendicular one to another (illustration at left). When the plane of oscillation doesn't change, light is linearly polarized (with circularly polarized light, the plane of electric field - with the plane of magnetic field perpendicular to it - rotates in time around its directional axis). Actual waves are generally unpolarized, i.e. their electric field randomly changes its orientation in space, a consequence of the ever changing position and orientation of the emitting atoms. While there is no actual circular motion present, it is convenient, as already mentioned, to represent oscillations as such, with the full phase of a wave - corresponding to the spatial period between two closest points in the same phase - equaling 2π radians.
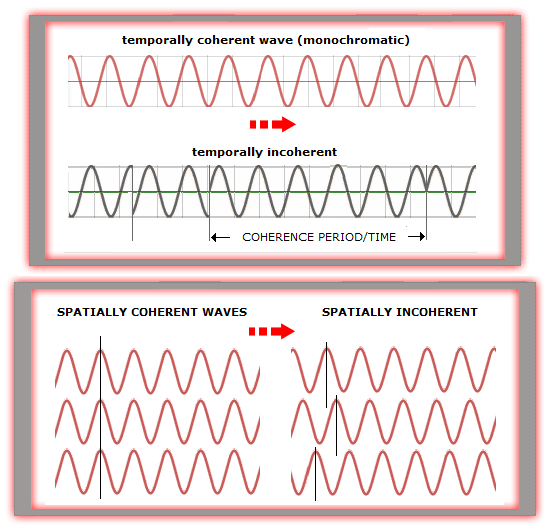Putting it in words, while coherent light waves, due to their consistent phase relationship, interfere in sustained manner, so that their amplitudes add first, and a square of their sum (complex amplitude) gives the combined intensity, with incoherent light the fields are essentially independent and the combined intensity is given by a sum of individual intensities, i.e. sum of the individual amplitudes squared. In other words, coherent light is linear in complex amplitude (square of which gives intensity), whereas incoherent light is linear in intensity, given by a sum of the squared individual wave amplitudes. Thus, for near-equal amplitudes and near-zero OPD, the maximum combined intensity doubles with the doubled flux for incoherent, and quadruples for coherent light. 
