|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
1.3.
Optical system of a
telescope
 Optical system
of a telescope consists from:
(1)
objective, which captures light
from faraway objects and uses it to form their real image, and
(2)
eyepiece, a sophisticated magnifying glass that
enables the eye to greatly enlarge projection of this image onto the
retina.
Telescope objective can be a single concave mirror; it can
also consist from two or more mirrors, or lenses, or of mirror and
lenses
combined. It gathers light and forms images of distant objects. While
the image it forms can be observed directly, the eye would only
receive a small fraction of the light emerging from it (FIG.
6).
It is the role of the ocular - or eyepiece - to make all the light
from the image formed by the objective available to the eye and, by increasing
apparent angles, add a significant magnification factor to the final
image formed on the retina (FIG.
7).
FIGURE 6: Image
formed by a telescope mirror objective, as seen without the eyepiece
(flat is omitted for simplicity). Wavefronts emitted from
distant object of height h become practically flat over
the aperture of a telescope, here a concave mirror M.
The mirror
changes the shape of the incoming flat wavefront section (W) into spherical (W')
by delaying reflection of the points
in phase
belonging to the wavefront's inner area. Point of
convergence (c) - or focal point - is at the center of curvature
R of the wavefront. Thus, with the stop at mirror surface and
exit pupil plane at mirror vertex, the mirror focal length
equals the radius of the wavefront in the pupil. The top
point of distant object h, at an angle
α
from the optical axis, is imaged into
(reversed) top of the image h'
by off-axis wavefront Wa,
originating at the object's top point. If observed directly, from the least
distance of distinct vision v (approx. 25cm, or 10
inches) most of the light from the
object image h' misses the eye pupil (more so for the
points farther off-axis, with no light from the image's reversed
top reaching the eye); also,
magnification is limited to ƒ/v,
ƒ
being the objective's focal length. The apparent image angle
β
determines objective
magnification as Mo=tanβ/tanα.
FIGURE 7:
Image formed by a telescope lens objective, as seen through the
eyepiece. Since light is slowed down in glass, the
in-phase points of
the incident axial wavefront W are retarded the most in the
center of the lens objective L (for simplicity, both
objective and eyepiece are shown as a single lens),
and the least at its edges. Properly made lens objective will
re-shape flat incident wavefront W into spherical
(W') after exiting the lens. That is a goal for off-axis
point wavefronts (Wa)
as well, although some form of deviation due to tilt-created
asymmetry is usually present. In terms of rays, change in
direction of straight lines orthogonal to the
wavefront (rays), resulting from its new shape, is called refraction.
The lens objective focal length
ƒO is the distance
between its second principal point P2
and the focal point F. The eyepiece (EP), placed at a distance of its focal length ƒE from the
object image h' formed by the objective, converts diverging
spherical wavefront into flat, for which the eye has preference.
It also
increases the apparent incidence angle (α
vs.
ε), making
the object imaged at the retina (E) appear larger by a
factor ~ƒO/ƒE.
Use of an eyepiece allows for far more light from the object's
image (all of it, if properly designed) to reach the eye,
much higher magnifications, and much wider fields compared to
observing image formed by the objective with eye alone.
The very basic element of a telescope is
the diameter of its
aperture.
Given optical quality, it is the main determinant of
telescope's capabilities with respect to light gathering and resolution, thus
also of its limits in useful magnification. If well made, the eyepiece has
no appreciable effect on the light gathering or inherent resolution of a telescope.
Its main function is magnification of the real image formed by
the objective. Consequently, the main optical parameters of a
telescope relate to its objective. They are:
● aperture
diameter, hereafter denoted by D
● focal length
ƒ and
● relative aperture
D/ƒ=1/F, with F being the
focal ratio
Thus, telescope consist from a single or
or multi-element objective, and
an eyepiece centered around the optical axis of the objective. The objective
forms the focal point - a point
of ray convergence on its optical axis (in terms of physical optics,
the point of the highest generated wave energy, but the two
generally coincide only in aberration-free system) - which determines the focal length of a telescope.
Telescope focal length is a
distance from the objective to where it focuses collimated light.
That is, when the light arrives
from objects far enough that the wavefront
entering the objective is practically flat, and the light rays
are practically parallel. In complex objectives, the effective focal
length is determined
from the focus separation s from the last surface and the
height of marginal ray hm
on it, as ƒ=sD/2hm (FIG.
8). For closer objects, the focus forms
farther away from the objective.
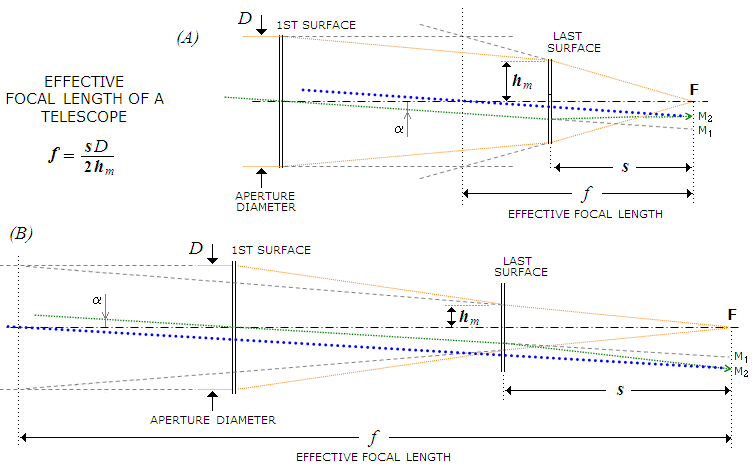
FIGURE 8: Effective focal length of
a telescope system with widely separated surfaces is obtained by
extending the final converging axial cone (after the last surface)
backward to the point of intersection with the height of the aperture.
It can be either shorter (A) or longer (B) than the physical separation
between the first surface and focus. The light convergence produced at
the last surface bends the chief ray (green) to produce the final system
magnification M2,
proportional to its effective focal length, not the surface-to-focus
separation. A line connecting M2
with the effective (virtual) aperture center (dotted blue) forms an
angle with the axis that is equal to the angle of incident light
α.
Linear size of the Airy disc is determined by the final angle of
convergence (i.e. by the effective focal ratio), while its angular size
(linear size divided with the effective focal length) remains that
corresponding to the aperture diameter (i.e. 2.44λF/ƒ=2.44λ/D,
in radians).
The definition
of focal length implies that an optical surface, or system, will have a
constant focal length only if it focuses all rays to a single point on
the path of the central ray. No actual system does since, due to the
presence of spherical aberration, the
location of focus varies with the ray height in the telescope pupil. For
a given aperture, the focal length is conventionally defined as that
with respect to the focal point formed by its marginal (edge) rays. So,
for a concave mirror of the vertex radius of curvature R,
aperture radius d, surface sagitta z and
conic constant K,
the focal length is defined by:
2ƒ=R+(1-K)z-d2/[R-(1+K)z)]
For spherical mirror, K=0 and 2ƒ=R+z-d2/(R-z)
which, knowing that the last term closely approximates 2z, implies ƒ<R/2,
with the differential between ƒ for d→0
and for d»0 defining the separation between two focus location, i.e.
longitudinal spherical aberration. The change in focal length for d»0
(marginal rays) vs. d→0 (paraxial) is opposite
in sign to R, implying marginal focus closer to mirror than
paraxial (under-correction).
For a
paraboloid, K=-1 and 2ƒ=R+2z-d2/R
which, knowing that z=d2/2R
for parabola, yields 2ƒ=R and ƒ=
R/2, with zero spherical aberration.
For K=-2 (hyperboloid), 2ƒ=R+3z-d2/(R+z),
with the same magnitude of longitudinal aberration as sphere, only with
marginal rays focusing longer than paraxial (over-correction).
Similarly, with object at infinity, any
lens with spherical
surfaces generates spherical aberration (positive lens under-correction,
negative over-correction).
In determining the basic image properties - its location
with respect to imaging element, and size (first-order optics) - system
aberrations are not a significant factor and can be neglected. The
simplified calculation following light passing through the central,
practically aberration-free portion of the optical surface/element is
called paraxial, or Gaussian
approximation.
◄
1.2. Reflection and refraction
▐
1.3.1. Gaussian approximation
►
Home
| Comments |