|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
2.3. Telescope magnification
Telescope magnification
is given by a ratio of the image size produced on the retina when
looking through a telescope, versus retinal image size with the naked eye.
As FIG. 7 shows, image
size on the retina in both cases is proportional to the apparent angle
of view, giving telescope magnification as MT=
ε/α, ε
and α
being the apparent and true (semi) angle of view, respectively. For
sufficiently small ε,
the angles relate nearly as their tangents. Replacing the two angles
- with their tangents (tanε=h'/fE
and tanα=h'/fO)
gives telescope magnification as:
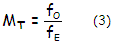
with fO,
fE
being the objective and eyepiece focal length, respectively. For
simplicity, both telescope and eyepiece focal length will be considered
numerically positive. Also, since most telescope objectives form
reversed objefct image, which is not changed by the eyepiece, their
magnification is, by definition, numerically negative; for simplicity,
it will be given as numerically positive here, since it is not used for
other (broader) calculations.

Since this
relation assumes small angle of view, it is strictly accurate only for
small angular objects, not larger than about 10 degrees in the eyepiece.
With the tangent increasing faster than the angle, large angular objects
in the eyepiece will have lower actual magnification than indicated by
this formula. For instance, a 1 arc minute object magnified to 1°
apparent size will have actual magnification of 60, exactly as the
formula indicates. But a 30 arc minute object magnified to 30° apparent
size will also have actual magnification of 60, while the formula
indicates 61.4.
Telescope magnification can be split
into two components: (1) magnification of the objective and
(2)
magnification of the eyepiece. Magnification of the image formed by
the objective is either relative to the object imaged (absolute, or
optical
magnification), or relative to its apparent size in the naked eye
(apparent magnification). The former is expressed with a simple formula:
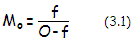
with
f
being the telescope focal length, and O
the object distance (FIG.
7).
Obviously, it is very small for astronomical objects, due to their
enormous distances. Apparent magnification of the objective is given by
the ratio of the viewing angle of its object-image from the least distance
of distinct vision (250mm average) to the viewing angle of the object
observed directly. Since these angles are sufficiently small, they can
be replaced with their tangents, giving the apparent objective
magnification as
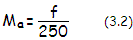
for the focal length
f in mm.
In terms of image-to-objective
separation I (also assumed numerically positive) the apparent
telescope magnification is Ma=(I-f)/f,
which determines the object distance in terms of I and
f as O=If/(I-f).
Due to enormous distances of astronomical objects - thus with I
only negligibly greater than
f - their absolute
magnification in a telescope approaches zero.
The eyepiece
acts as a magnifying glass, effectively allowing the eye
to observe the object-mage formed by the objective from the distance of
eyepiece's focal length
(fE in
FIG. 7). It makes the image apparently larger by a factor
ME=
ε/β,
with ε
and
β
being the apparent viewing angle in the eyepiece and in the naked eye
(the latter also called "true" angle, or field of view),
respectively (FIG. 6-7).
Again, for small to moderate viewing angle ε, we can replace angles with their tangents (tanβ=h'/V~h'/250
for h' in mm), giving the eyepiece magnification factor as
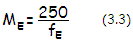
for
the eyepiece f.l. fE in mm. Thus, apparent telescope magnification is a product
of the two magnifications - the initial apparent magnification by the objective,
and the final one by the eyepiece - resulting in Mt=MaMe~f/fE.
Of course, the eyepiece magnifies by enlarging the apparent angle of
rays converging toward the eye,
but it produces collimated beams and, thus, no actual image. It is the eye
that focuses these collimated beams into point images.
As noted, for large viewing angles in the eyepiece, use of the tangent
results in higher than actual magnification figure. For instance, a 5mm
high object-image on the optical axis is viewed through a 50mm f.l.
eyepiece at an angle
α
given by tanα=5/50,
giving α=5.7
degrees apparent viewing angle. And that same object-image observed
through a 10mm f.l. eyepiece has the apparent viewing angle
α'=26.6
degrees. While the tangent (i.e. eyepiece f.l.) based magnification
factor is 5, actual magnification factor for the 10mm vs. 50mm eyepiece
is 26.6/5.7=4.7.
While there is no
single optimum magnification for all types of astronomical objects and
individuals, there is a range of so called useful magnification. On the low side of
this range, the limit is set by the size of eye pupil. It is not to be
smaller than the "exit pupil" of a telescope - an image of the entrance
pupil (objective) formed by the eyepiece. Exit pupil appears as a bright
circle of light floating in front the eyepiece eye lens (the eyepiece lens facing the eye). In
order to capture all the light entering telescope, the eye lens has to
be placed at the location of exit pupil and, of course, in order to
avoid light loss, eye pupil
has to be at least as wide as the exit pupil. Since the exit pupil diameter is given by
P=D/Mt=fE/F, the lowest magnification that still preserves
light-gathering power is Mt=D/Pmax.
For the average eye pupil maximum of 6mm, it comes to D/6 for D in mm.
Limit to magnification increase is set
primarily by image imperfections, but also by dimming, loss of field,
vibrations and eye physiology. As we have seen, even perfect optics will
not produce perfect images, due to the effect of
diffraction.
Point-object image is smeared into a pattern of finite size. Magnified
enough (to about 4 to 5 arc minutes) it becomes visible to the eye, and
there is no benefit in resolution from further magnification increase.
Taking the standard resolution limit for a pair of near equally bright
point sources of 4.5/D (D in inches) arc seconds (1/13D in arc
minutes), needed magnification to 5 arc minutes apparent center separation for a
pair of relatively bright point-object images at the resolution limit is given as ~67D,
or 67x per inch of aperture (~2.7D for D in mm).
The often quoted 50x per inch of aperture limit to
useful magnification dates back to the 1940s, when Allyn Thompson used a
mixture of theoretical diffraction resolution limit for point-like
sources, anecdotal accounts of the limit to naked-eye stellar resolution
(ε Lyrae), and the results of group's own experiments with naked-eye
resolution limits for pairs of 0.0003-inch illuminated pinholes, to come
up with four arc minutes as the approximate average resolving limit for
point-like objects (Making your own telescope, p173-174).
Combining it with the Dawes' limit formula for the minimum resolvable
stellar separation in arc seconds α=4.56/D
for the aperture D in inches, for the corresponding
magnification M needed to enlarge this limit to four arc minutes
(i.e. 240 arc seconds) apparent size, produced M=240/α=52.6D.
In line with this, higher magnifications than ~50x
per inch of aperture would not produce additional benefit.
However, Thompson's consideration missed to recognize
that telescopic and naked-eye point-source resolution are distinctly
different. The former is limited by diffraction, and the latter by
aberrations. At 4mm pupil diameter, which was the estimated pupil size
level in their experiments with pinhole resolution (the naked-eye pupil
size while resolving ε Lyrae is at least as large), eye not corrected
with ophthalmic lenses averages about 1 wave RMS of (mainly) combined
defocus and astigmatism. The resulting diffraction blur is roughly a
dozen times larger than the Airy disc and, more importantly, its angular
size is about 8 arc minutes, decidedly larger than the maximum
angular size still perceived by the eye as point-object.
Unlike the naked-eye observer, telescope user has the
benefit of eye defocus error corrected by refocusing the eyepiece. This
reduces the RMS error by a factor of four, or so, with the diffraction
blur shrinking nearly as much, to about 3 arc minutes (FIG.
236A). Hence the average
telescope user would need only about 1/3 of the magnification calculated by
Thompson - about 17x per inch of aperture - for the theoretical
resolution of two point objects at the Dawes' limit. The corresponding
eyepiece exit pupil - and the effective eye pupil - is about 1.5mm in
diameter, at which the average eye is better than diffraction-limited,
and telescopic eye - due to corrected eye defocus error - decidedly
diffraction limited.
However, since the FWHM angular diameter at this magnification level is
still only 1.26 arc minutes, or about 2.5 arc minutes for two touching
FWHMs combined (lengthwise), the image is still too small for the eye to
clearly discern its shape. For that, the combined image needs to be
further enlarged to about 5 arc minutes (~34x per inch magnification).
Increase in magnification up to twice as much (70x per inch, with each
FWHM enlarged to about 5 arc minutes) still results in small gains, and
is needed to achieve the ultimate resolution limit.
Obviously, taking the naked eye resolution limit as a
criterion for the telescopic resolution was inappropriate, but the
result obtained for needed magnification - 50x per inch - happened to be
a good approximation of the actual magnification level needed to reach
the diffraction limit to stellar resolution.
In the field use, induced telescope aberrations,
particularly seeing error, can
significantly worsen resolving limit, as illustrated on FIG 19.
Follows more detailed consideration of the factors related to the
limiting stellar resolution, and its characteristics.
A simple consideration based on the retinal
physiology (FIG. 18 left) indicates that foveal resolution of two patches of light
requires them to be separated by at least a single non-illuminated cone,
as the illustration below shows. With the smallest cones being less than
half arc minute in diameter (about 2 microns), the limit of resolution
of two diffraction discs that don't exceed about 1/2 arc minute in
diameter is approximated by about twice the cone diameter, or 0.8 arc
minute. Since the discs' centers are separated by twice their diameter,
the corresponding angular separation is about twice the disc's angular
diameter. Taking that this diameter is FWHM of the PSF, or λ/D, on
average, (somewhat smaller for faint, and somewhat larger for
bright stars), this separation corresponds to double the stellar
diffraction limit of resolution, λ/D.
In theory, the minimum could be somewhat better, if
the star images are smaller than a cone, and positioned closer to the
edge of its respective cone. For instance, star images of about 1/5 of
the cone diameter could be positioned at about 1/10 of its diameter from
its edge, with the minimum separation of about 1.2 the cone diameter,
i.e. 0.5 arc minute. This is the apparent angular separation; to relate
it with the actual angular separation of two stars, we need to consider
the magnification factor. Taking again the diffraction FWHM (λ/D in
radians, or 3438λ/D in arc minutes which, substituting λ=0.00002165 for
λ and D in inches, comes to FWHM'=1/13.43D arc minutes) as the
limiting resolution factor. Expressing the nominal (actual)
magnification MN
per inch of aperture, as M=MN/D,
the apparent size (diameter) of FWHM is:
FWHMA =
MN
x FWHM'= MN/13.43D
= M/13.43
Thus, for the stellar FWHM to reach 1/5 of the cone diameter, or 0.08
arc minutes requires MN=D(inches)
nominal, and M=13.43x0.08=1 per inch of aperture magnification.
Obviously, this is impossible, since it requires
eyepiece exit pupil (given as E=D/MN,
or E=1/M, E being the exit pupil diameter) as large as 1 inch. For the conventional limit to the exit pupil size of
6mm (0.236 inch), equaling the maximum iris opening for the average eye,
the corresponding magnification per inch of aperture is M=1/E=4.24.
Hence, the corresponding smallest apparent FWHM on the retina is
0.08x4.24=0.34 arc minutes, about 15% less than the cone diameter. It implies
that the minimum resolution of two such FWHMs could be 7-8% smaller than
2λ/D. However, this could only occur if the size of FWHM image projected
onto retina is not significantly affected by eye aberrations. This is
not the case. As FIG.
236A illustrates, aberrated blur (corrected for eye defocus, as it
is for the telescopic eye) at M~5x and E~5mm spans nearly 10 microns, or
3-4 arc minutes (this, of course, vary with both telescopic star
brightness and individual eye aberration level).
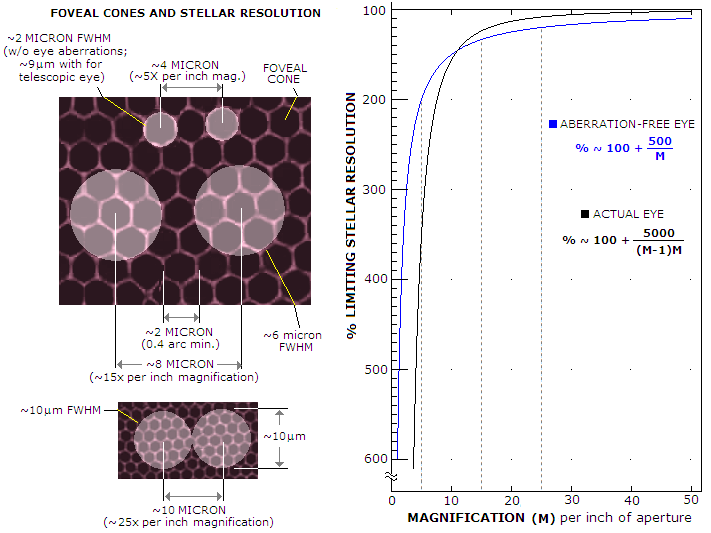
FIGURE 18: LEFT: Illustration of the resolution concept based
on the foveal cone size. They are about 2 microns in diameter, or 0.4 arc
minutes on the retina. Angular diameter of the diffraction FWHM in a
telescope of aperture D is ~λ/D in radians, or 3438λ/D in arc minutes,
λ being the wavelength of light. For the typical range of amateur
apertures from 4-16 inch and λ=550nm, it ranges from 0.019 to 0.0047 arc
minutes. It is much smaller than the cone, but its apparent angular size
on the retina is larger by the telescope magnification factor. Top: At ~5x per inch magnification,
diffraction FWHM is enlarged to the angular size of foveal cone, with
the corresponding limiting resolution being about double the resolution
limit λ/D, or 2λ/D. This, however, assumes aberration-free eye; since at this low
relative magnification the exit pupil is still quite large, the actual FWHM is significantly enlarged by
eye aberrations, and the resolution is
significantly lower. More specifically, the bright central portion of
diffraction blur at ~5x per inch magnification, and corresponding ~5mm
eyepiece exit pupil diameter, is approximately 3-4 arc minutes (varies
with the star brightness). Since this blur spans about 6-8 foveal
cones, the minimum separation needed for resolution is about 7 cone
widths, or 3 arc minutes. As a result, actual limiting resolution at
this magnification level is more than three times worse than what it
would be without eye aberrations, or ~7λ/D.
Doubling magnification to 10x per inch produces ~2.5mm eyepiece exit pupil, at which
the telescopic eye, corrected for defocus, is better than diffraction limited, with the limiting
point-source resolution practically identical to that of aberration-free
eye. The size of aberrated blur shrinks rapidly with smaller pupils, with the eye error
reaching diffraction-limited maximum at about 7x per inch magnification
(i.e. ~3.5mm diameter). At 15x per inch magnification,
limiting resolution is about 4/3 the diffraction FWHM, or 1.3λ/D (middle).
The FWHMs are shown with a non-illuminated cone in between, but they
already cover enough cones that it may not be needed for resolution. It
is notneeded at 25x per inch (bottom).
RIGHT: Plot of the % of stellar resolution limit as a function of
telescope magnification for the actual, aberrated (black) and
hypothetical aberration-free eye (blue). At 20x per inch, telescope
resolves close to 110% (i.e. 10% larger separation than the diffraction
limit), only about 5% better than at 30x per inch.
As mentioned, telescopic eye is diffraction limited
at exit pupil diameters of about 3mm and smaller, corresponding to
magnifications of about 8.5x per inch and higher. At 10x per inch
magnification, the stellar FWHM is about two cones (4 micron, 0.8 arc
minute apparent) in diameter, with the resolution limit near that of the
hypothetical aberration-free eye, but the eye still cannot resolve two
FWHMs at the diffraction resolution limit, i.e. those nearly touching in
the image of the objective. The reason is that too few cones are
involved in detection, requiring at least a single non-illuminated cone
between two FWHMs, and its angular size still being too small for the
eye to discern the shape of two adjoining FWHMs. For that, their size
needs to approach 5 arc minutes combined, which requires magnification
of nearly 30x per inch. At this point, the FWHM spans over a dozen of
cones, and there is no need for a non-illuminated cone between two FWHMs.
However, since it is a threshold level for the average eye, further
increase in magnification allows still better resolution, although the
gain is relatively small. At 50x per inch - which is what Dawes' needed
to achieve its limiting resolution - each FWHM is 4 arc minutes in
diameter - 8 arc minutes combined, when touching - and the resolution limit
is practically reached.
Actual neural processing involved in eye's visual
function is, of course, much more complex. But this simplistic concept
suggest that gain in stellar resolution does not scale linearly with
magnification increase. It is higher when magnification increases in the
lower range, gradually decreasing with higher magnifications, and
falling to negligible at about 50x per inch of aperture, and beyond, as
the above graph shows.
However,
by assuming diffraction-limited resolution, this concept neglects the
effect of atmospheric error on the diffraction pattern. Magnifications
enabling diffraction resolution may not be attainable in field conditions;
reaching 105% of the stellar diffraction limit would require 30x per inch of
aperture magnification, or about 120x and 240x for 4-inch and 8-inch
aperture, respectively.
Near 100% resolution twice as much. As aperture increases, typical seeing causes break-down and expansion of
the diffraction FWHM, causing telescopic resolution - and corresponding
magnification - to become seeing limited. In the typical 2 arc
seconds seeing, apertures from about 8 inch in diameter up will have
their resolution limit and magnification needed to reach it
progressively decreasing. Long-exposure FWHM expansion is approximated by a
(D/r0)
ratio (for r0≤D),
where r0
is the atmospheric coherence length (nearly 3 inches for 550nm
wavelength in 2 arc sec seeing, changing inversely to the
seeing). The short-exposure expansion is, in the
common 1<(D/r0)<5
range roughly half as large, or approximately given by a
(D/2r0)
ratio (for
r0≤0.5D),
as illustrated on FIG. 79,
bottom.
An arbitrary
approximate adjustment is made for the visual FWHM, which in the low D/r0
range is closer in size to the short-exposure FWHM, gradually becoming
nearly as large as long-exposure FWHM beyond D/r0~5.
The resulting seeing-limited optimum magnification (red, with the
"optimum" defined as one needed to achieve limiing resolution for given
seeing FWHM), as well as needed
magnifications for diffraction-limited stellar
resolution w/o seeing (straight lines) are as plotted at left (FIG. 19). It is assumed that
stellar resolution is near diffraction-limited (i.e. aperture-limited)
for D/r0<2,
gradually deteriorating to the seeing limited (i.e. r0
alone limited)
resolution for D/r0~5
and larger, based on the relation
between r0
and seeing FWHM.
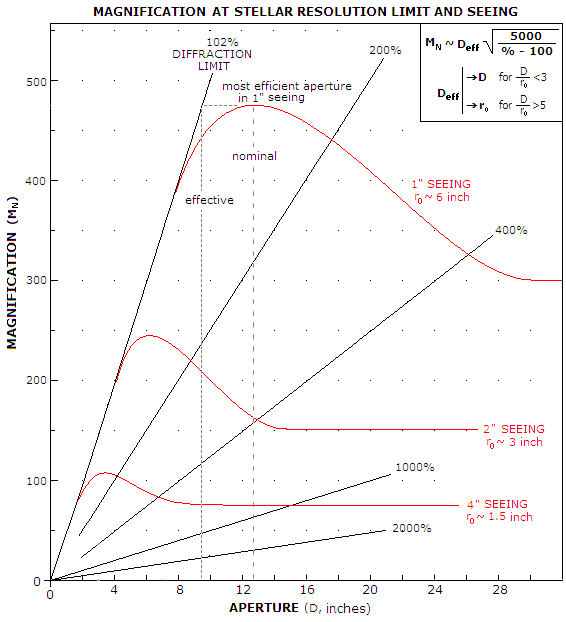
FIGURE 19: Actual telescope magnification
MN
needed to achieve limiting resolution for given seeing FWHM (red) as a function of aperture diameter D, plotted
against selected levels of stellar resolution (straight lines; as
before, values larger than 100% indicate resolution limit proportionally
larger than diffraction limit). Value of MN
is obtained from
approximation for the actual eye resolution on FIG. 18 (right), and 102%
of diffraction-limited stellar resolution, achieved with ~50x per inch magnification, is used as the starting point
for plotting seeing-limited magnification. The graph shows two
general trends:
(1) as seeing deteriorates, maximum nominal
magnification decreases for all aperture sizes, and (2) maximum nominal
magnification - and stellar resolution limit - shifts toward smaller
apertures. In 1 arc second seeing, the maximum seeing-limited nominal
magnification is in the 12-14 inches aperture range, and it is
effectively at the level of 9-10 inch aperture. At two arc
seconds seeing, it is in the 6-8 inches range, and in 4 arc second
seeing maximum magnification is attainable with apertures somewhat smaller than 4
inch in diameter. The graph also implies that reaching diffraction limit
of resolution becomes increasingly more difficult - or impossible - as
the aperture diameter increases, due to the greater restrictions to the
relative (in units of aperture) magnification for larger apertures,
imposed by seeing (assumed is telescope optical quality sufficiently
high not to be a significant factor for stellar resolution, which
generally implies error smaller than 0.15 wave RMS).
Note that the magnification plot (red line) indicates
the level at which the stellar resolution limit is approached, not the
highest possible magnification. For instance, a 16-inch in 2" seeing has
D/r0=5.3,
and the resolution limit gravitating toward that of an aperture equaling
r0,
i.e. 3 inch, which is the effective aperture diameter for stellar
resolution (Deff).
Thus the nominal magnification required for reaching 102% of the
resolution limit is MN~Deff[5000/(102-100)]0.5=150,
about the same as if it is for 3-inch aperture in perfect seeing (as indicated by
extending the level of magnification indicated by the red line to the
left, where its intersection with magnification needed for 102%
resolution in perfect seeing determines the corresponding effective
aperture). Somewhat higher magnification than that still can be useful.
The ~1000% of the diffraction resolution limit maximum
resolution line intersecting with the red plot for 4 arc seconds seeing
at about 15-inch aperture implies that the averaged angular size of its
seeing-expanded FWHM is about ten times larger than
in the aberration-free aperture, i.e. at the level of 1.5 inch
aberration-free aperture.
It is very important not to forget that seeing
constantly fluctuates. At any averaged seeing level, there will be
periods with better, or worse seeing than the average. Simplistic
schematics on FIG. 82
implies that roughly 25% of the time seeing is 25-50% better than the
average, i.e.
r0
is about that much larger. Similarly, about 25% of the time seeing is
25% or more worse than the average. In other words, the above plots
actually represent the minimum resolving magnification in brief moments
when the actual seeing is at its averaged level. In any extended period
of time, the magnification value covers wider range, approximately ± 50%
from the average. Hence the optimum aperture size is one that is biased
toward the moments of better seeing. If, for instance, we choose to
center it around the better half of the time, then it is about 25%
larger than one optimal for the averaged seeing. On the above graph,
that would imply 4.5, 8 and 16 inch aperture for the averaged 4, 2 and 1
arc second seeing.
This is a very approximate model, but it does
indicate, even roughly, the magnitude of seeing-induced reduction in the
limiting stellar resolution - and corresponding minimum resolving
magnification needed to rich the stellar resolution limit - for the range of apertures.
Again, keep in mind
that seeing constantly fluctuates, and so do the effective aperture and
corresponding magnification needed for 102% of the stellar resolution
limit (in 2" seeing average, fluctuations are likely to be mainly
within 1.3" and 3"
range, or so).
In addition, just as the
"standard" resolution limit is strictly valid only for a very particular
object type, as explained above, so is the high magnification limit
derived from it. Some objects - generally bright extended objects with
low inherent
contrast, like planets - will dictate lower maximum useful
magnification, while more contrasty, like Moon or brighter doubles, as
well as dim deep-sky objects, will allow - or demand - higher
magnification level.
As mentioned, the practical limit to useful
relative magnification on its high end will be generally lower, the larger aperture the more so - due to
the increase in wavefront aberrations in general, and especially the "seeing
error": the deterioration of image quality caused by atmospheric turbulence.
Also, optimum magnification varies rather significantly
individually, due to the differences in eyesight quality and observing
experience.
◄
2.2. Telescope resolution
▐
3. TELESCOPE ABERRATIONS
►
Home
| Comments |