|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS ◄ 2.3. Telescope magnification ▐ 3.2. Ray (geometric) aberrations ► 3. TELESCOPE OPTICAL ABERRATIONS: Types and causes
PAGE HIGHLIGHTS Any deviation of the wavefront formed by a telescope from perfect spherical - for wavefronts formed by the objective - or from perfect flat for wavefronts formed by the eyepiece, results in an optical aberration. Aberrations disturb optimum convergence of the energy to a point-image, with the result being degradation of image quality. The two main forms of measuring an aberration are:
(1) at the wavefront itself, as a deviation from the perfect reference
sphere, and
The former are known as wavefront aberrations; the later as ray, or geometric (ray) aberrations. Either aberration form has its purpose. While the wavefront aberration form is more directly related to the physical fundamentals determining image quality, ray aberration form offers more convenient graphical interface for the initial evaluation of the quality level of optical systems. Since the wavefront and the rays emerging from it are directly related, there is a constant relationship between the size of wavefront aberration, and that of corresponding transverse ray aberration relative to the size of the Airy disc. This is true for any given relative aperture; obviously, change in relative aperture for any given size of the transverse aberration relative to the Airy disc (i.e. for any given wavefront error) requires the relative longitudinal aberration to change inversely. Unrelated to the form of presentation of aberrations, it is useful to make a distinction between aberrations that are intrinsic to optical surfaces in their proper alignment, and those induced by external factors. Intrinsic telescope aberrations are those inherent to conical surfaces, to glass medium, and those resulting from fabrication errors.
Externally induced
telescope aberrations are
caused by: (1) alignment errors, (2)
forced surface deformations
caused by
thermal variations, gravity and improper mounting, and (3)
air currents/turbulence. 3.1. WAVEFRONT ABERRATIONSAs described in previous chapters, imaging quality of a telescope rely on optical surfaces capable of producing spherical wavefronts for the image formed by objective, then transformed into flat wavefronts by the eyepiece. The final wavefront is formed by the eye, ideally of spherical shape. Spherical wavefront ensures tightest possible energy concentration in the image of a point-source and, consequently, highest contrast and resolution. In other words, the effect of diffraction, which causes the point-object image to form as a bright central disc surrounded by a number of fainter concentric rings of rapidly decreasing intensity, is at its minimum for perfectly spherical (aberration-free) wavefront. Thus perfect telescope is the one that produces flat wavefronts exiting the eyepiece. While any combination of aberrated wavefronts at the objective and eyepiece that cancel each other out will do the trick, it is preferred to have the objective producing a near perfect spherical wavefront, and the eyepiece turning it into near perfectly flat. After that, it is up to the eye how accurate will be the final wavefront: the closer to spherical, the better. For most people, the wavefront formed by the eye becomes nearly spherical at ~2mm pupil diameter, and practically spherical at ~1mm pupil. The larger eye pupil, the greater wavefront deviations from spherical, due to eye's optical imperfections. This, in general, has less of an effect, with larger exit pupil sizes being associated with low-power observing, when wavefront imperfections are in general more forgiving. Wavefront quality is critical for high-magnification observing at small pupil sizes, when the eye, as mentioned, produces near-spherical wavefronts, provided it is supplied with near-perfect flat wavefront by the telescope. Any
significant deviation from
spherical in the shape of the wavefront formed by telescope's objective results in
lower quality of its image. Assuming no aberration contribution from the
eyepiece, this wavefront deformation will be transferred to the eye as
an imperfectly flat wavefront coming out of the eyepiece, passing the deviation to the wavefront formed by the eye. Since the path
length of a wave from any deviant, or aberrated point on the wavefront differs from
the wavefront radius' length, it arrives at the focal point out of
phase with the waves coming from the spherical portion of the wavefront.
The greater wave path difference, the greater
its phase difference,
and the lower wave energy contribution at the focal point (up to 1/2 wave path difference; from 1/2 wave to 1 wave the contribution is increasing, as shown on the graph on the page bottom). The more such
points on the wavefront, the more energy transferred to the outer
portion of diffraction pattern, and the lower image quality.
The existence of path difference at the focal point implies that there is a point - or points - farther off in the image space for which the wave path difference from aberrated points at the wavefront is now smaller, and constructive energy interference greater, than in a perfect system. In other words, that the energy lost from the proximity of the focal point due to wavefront aberrations will be effectively transferred toward outer area of the diffraction pattern. Deviation of any single point on the wavefront will not cause measurable effect on image quality, regardless of its optical path difference; however, if an area of the wavefront deviates from spherical, it will negatively affect image quality, the larger area, the more so. Energy concentration at the center of diffraction pattern becomes noticeably lower relative to energy contained in the diffraction rings, blurring the point image. The image quality of point-source deteriorates, and with it image quality of extended objects (the latter being merely point-image conglomerates). In terms of loss of resolution, expectedly, low-contrast details are affected more than those of high inherent contrast.
Wavefront deviation is commonly presented with the reference sphere as a straight line. This wavefront deviation form shouldn't be confused with the wavefront itself. Picture at left illustrates the relation between the wavefront and wavefront deviation for three common aberrations, defocus, primary spherical and coma. The actual wavefront converging toward focal point is always for all practical purposes spherical, with the deviations from spherical usually being a small fraction of micron, with the wavefront deviation form always greatly exaggerated.
The values of maximum positive and
negative wavefront deviation from the reference sphere combined determine peak-to-valley (P-V)
wavefront error. This figure alone is meaningless with respect to the damage it
causes to image quality, unless related to a known
form of wavefront deformation. In other words, unless both maximum
wavefront deviation from spherical, as well as the wavefront form are known (FIG. 21). An example of such forms of
wavefront deformations are those characteristic of the typical optical surface,
conic of revolution - spherical aberration, coma, astigmatism, field
curvature and distortion. Below are 3D plots of the three classical aberrations and
defocus.
The only useful input
from the P-V figure alone is that it approximates the worst case
scenario; that is, if the specified P-V error affects most or all of the
wavefront area, it cannot be significantly worse than a wavefront with
this level of P-V error of spherical aberration (assuming that
larger-scale surface roughness is not significant). So 1/10 wave P-V
mirror with reasonably smooth surface cannot be significantly below the
quality level of 1/10 wave P-V of spherical aberration; on the other
hand, it is possible that 1/4 wave P-V mirror, with the deviation
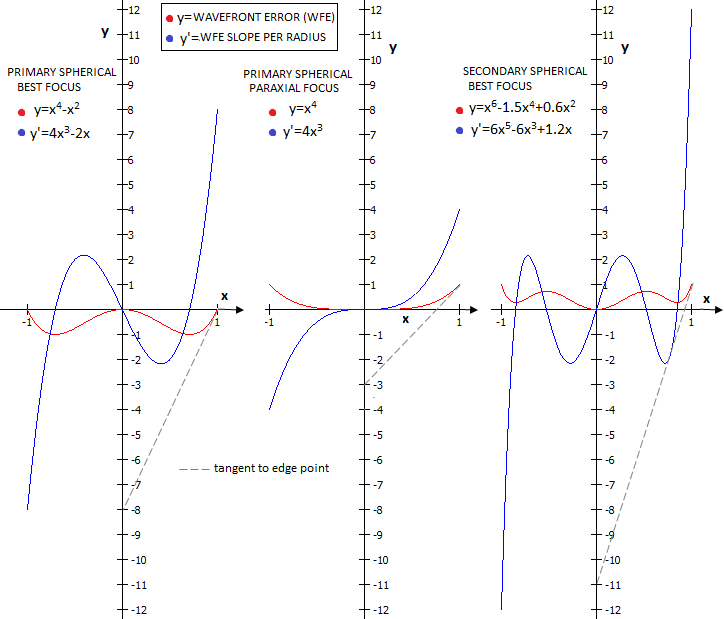
limited to a small wavefront area, performs as well, or better. Potentially significant indicator of wavefront quality is its slope, i.e. dynamics of change in the wavefront error over its radius. Wavefront slope is generally expressed as the change in optical path difference vs. change in radius value, i.e. ∆OPD/∆d, which for wavefront aberration expressed as f(x), x being the pupil zonal radius, determines its first derivative f'(x). It can be given for a section of wavefront radius, expressed either in linear or angular units. For any point at the wavefront, the slope is determined by the tangent to the wavefront for that point, as shown on the graphs below.
At left are shown wavefront deviations for primary spherical aberration at the best (left) and paraxial focus (middle), as well as for balanced secondary spherical (right), all for unit P-V error. Wavefront slope is measured in the units of wavefront error (WFE), as a projection of the tangent section over the radius onto the vertical (wavefront error) scale. The corresponding value for any point on the wavefront is given by the first derivative (y', blue plot) of the aberration function (y, red plot). For the edge point, slope for primary spherical at the best focus is 8 times the P-V error, while only 4 times at the paraxial focus. For balanced secondary, the slope is 12 times the P-V error. For the first two, the slope difference is not affecting optical quality, since the P-V to RMS ratio for either wavefront form is identical. For the balanced secondary spherical, the ratio is 1.6 times higher (which means that at the comparable RMS error level it would have as much higher edge slope, i.e. over 19), a consequence of the real steep portion at the edge covering less than 10% of the radius, and the secondary P-V maxima being smaller and at the lower, ~0.5 zone. It would, however, change for the worse, if wavefront slope would fluctuate in this same range over the radius, i.e. with the presence of a large-scale wavefront roughness. And even if balanced secondary spherical has more favorable P-V to RMS wavefront error ratio, it lags a bit behind with respect to encircled energy efficiency, having its bright rings energy spread out wider. Simplifying the Mean Value Theorem by limiting the aberration function to (0,1) interval, gives the average slope of the wavefront as equal to its first derivative value for x=1, in this case y=f'(1)=2. Given that, mean slope value is determined by the value of x for which f(x) first derivative f'(x) equals f(1), which is here also equal to the average slope value. This value of x is found by equating the second derivative of the aberration function to 2 (since that means that the slope of the tangent to f'(x) at this point is parallel to the average slope). An example is given for the best focus primary spherical. 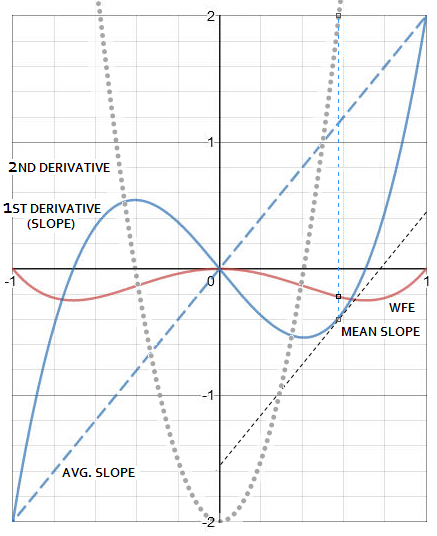
Line connecting the ends of the wavefront error plot (WFE) represents its average slope (dashed blue, left). Here, average slope has the same value as the edge point slope (i.e. it is parallel to the tangent to the edge point), so it is also eight times the P-V wavefront error. Mean slope is, for 0≤x≤1, given by the point on the slope plot (solid blue) whose tangent is parallel to the average slope, i.e. for the value on the horizontal scale for which the second derivative of the aberration function - i.e. derivative of its first derivative - equals the aberration function for x=1, in this case 2. The general derivative form, f'(xn)=nx(n-1), gives for the aberration function f(x)=x4-x2, f'(x)=4x3-2x and f"(x)=12x2-2, so the value of x for which f"(x)=2 is √1/3, or x=0.5774. Substituting this value into the first derivative (slope) function gives the mean slope value as f'(x)=-0.385, or 1.54 in units of the P-V wavefront error, determined by the maxima of the aberration function f(x)=x4-x2 (-0.25 for x=√0.5). Should be noted that wavefront slope is not directly related to surface slope. In all three examples above, the surface is a perfectly smooth conic of revolution, with the optical path difference, representing the wavefront error, created as a difference between the actual surface and a perfect reference paraboloid (for object at infinity). Larger local surface errors can either reduce, or enlarge the total error - for instance, a wide zone centered at 0.7 radius, if of opposite sign, would diminish the primary spherical aberration error, if smaller than double its value - while the small surface roughness would mainly add wide angle scatter. The sign of the P-V wavefront aberration is determined by the optical path length: if it is larger than a perfect reference path (i.e. if the wave has to travel an extra length to reach the focus), the P-V error is positive, and vice versa. The term "optical path length" refers to the path length that the light wave travels in a given time, determined by the optical path length of the chief ray (the central ray of the wavefront); therefore, it is directly dependent on the speed of light through optical media and may differ from the geometric path length. This is why the error on, say, mirror surface (the medium is air), results in different optical path length - and error magnitude - than nominally identical error on the lens surface (the mediums are air and glass).
The extent of image deterioration caused by wavefront deformations is much more reliably determined by its deviation from spherical averaged over the entire wavefront. It is the so called root-mean-square (RMS) wavefront error, usually expressed in units of the wavelength of light. The RMS wavefront error is given by a square root of the difference between the average of squared wavefront deviations minus the square of average wavefront deviation, or RMS= <(W-<W>)2>1/2 = (<W2>-<W>2)1/2, with the <...> brackets indicating an average value. For instance, if we measure wavefront deviations at three points, for simplicity, as 0.5, 0.2 and 0.1, the average of their squared values <W2>=0.1, while the square of their average value <W>2=0.071. The RMS error would be given as RMS=√0.1-0.071=0.17. In more general terminology, the RMS error is what is statistically known as standard deviation, which is given as the square root of variance, defined as the average of the squared differences from the mean value. In the case of a wavefront, the mean value is that of the deviations from perfect at all measured points. Taking the same three values from above, the mean is (0.5+0.2+0.1)/3=0.2667, and the variance is [(0.5-0.2667)2+(0.2-0.2667)2+(0.1-0.2667)2)]/3=0.02889 and the standard deviation - or RMS wavefront error - is, again, √0.02889=0.17. Throughout this site, the RMS wavefront error is denoted by ω, and the P-V wavefront error (occasionally also peak wavefront error) is denoted by W. The RMS value expresses statistical deviation from perfect reference sphere, averaged over the entire wavefront. Since derived from squared values, the RMS error is independent of the sign of P-V wavefront deviations, thus always given as an absolute (positive) number. To be meaningful, the RMS wavefront error must be calculated for a large number of points on the wavefront (or optical surface, for surface RMS). By being an indicator of the average optical path deviation over the entire wavefront, the RMS wavefront error is closely related to the cumulative phase loss at the center of diffraction pattern and, hence, to its peak intensity. Phase variance over the pupil can be written as φ2 = <(Φ-<Φ>)2>=(<Φ2>-<Φ>2)=(2πφ)2, where Φ is the phase deviation, in radians, varying over the pupil, and φ is the phase analog to the RMS wavefront error (with the former in units of full phase, or 2π, and the latter usually in units of the wavelength). Also, the phase deviation Φ is analog to the OPD. The significance of phase variance is that the image point at which it is at its minimum determines so called best focus (also, diffraction focus). While best focus often practically coincides with the point of minimum OPD (wavefront) RMS, it is possible that the two differ significantly, as explained ahead.
Table below summarizes the meaning of
wavefront vs. phase aberration, including basic related terms.
Despite being directly related nominally,
the two forms of deviation (OPD/wavefront/RMS and phase) are not
necessarily commensurate. The reason is that both OPD and RMS derived from it
are based on the nominal linear
For that reason, a nominally large deviation affecting relatively small wavefront area (for instance, a narrow zone, turned edge, tube currents or seeing error) will have disproportionately larger effect on the OPD/P-V/RMS deviation value, than on the phase deviation value. Since it is the cumulative phase deviation that determines central diffraction intensity and the overall intensity distribution within diffraction pattern, both P-V and RMS values of this type of errors disassociate from the phase error, indicating larger than actual damage to the image quality - the larger magnitude of such aberrations, the more so. As a result, the Strehl value calculated from RMS-based approximations will be lower, possibly significantly, than the actual Strehl, determined by the cumulative phase deviation. Discrepancy between the wavefront and phase RMS becomes potentially significant as the former exceeds 0.15λ. At the RMS wavefront values of about 0.25λ and larger, it is quite possible that a significantly higher RMS wavefront error produces better Strehl value (although still in the single ratio points at best). For instance, at 1 wave P-V of primary spherical aberration at mid focus, diffraction maximas occur at the points 33% closer and 33% farther away from paraxial focus, despite the P-V/RMS wavefront error being still the lowest at the mid focus (FIG. 36B). For instance, image deterioration due to turned edge will be increasing with the TE magnitude only up to a certain level, after which further increase in the nominal RMS wavefront error will have little or no effect. For mirror edge, and 0.95% TE, this level is at about 1 wave P-V, or 0.13 wave RMS. At this point, central diffraction intensity is reduced to ~0.92. Increasing the error to 2 waves P-V, or 0.26 wave RMS, causes near negligible drop in the central intensity, down to ~0.91. Further error increase has practically no effect, as the ratio of constructive vs. destructive wave interference at the focus remains nearly unchanged. Similar effect will be observed with narrow zones (which can't cause more of diffraction disturbance than a matching ring-like obstruction, no matter how many waves RMS deep), or any other type of local wavefront deviation. However, for relatively small deviations - generally less than λ/2 - smoothly distributed over all, or most of the wavefront, the cumulative OPD/RMS and phase deviations will be closely related, indicating very similar to nearly identical level of aberration in the common range of their magnitudes in telescopes.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Picture at left illustrates ray path through a lens. Rays - by definition normal to the wavefront - from faraway object enter the lens parallel with lens' optical axis. However, due to lens' curved shape, the central ray, or
Picture at left illustrates ray path through a lens. Rays - by definition normal to the wavefront - from faraway object enter the lens parallel with lens' optical axis. However, due to lens' curved shape, the central ray, or