|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
3.1. Wavefront aberrations
▐
3.3. Conics and aberrations
► 3.2. Ray (geometric) aberrationsWavefront deformations are inevitably accompanied by disturbance of rays - by definition straight lines, or light paths - orthogonal to the wavefront surface. Disturbance of rays caused by wavefront errors manifests as angular deviation of the aberrated ray, producing linear ray deviation in the image plane, usually either from Gaussian image point, or from best (diffraction) focus. Note that the condition for light rays to remain straight is homogenous media. This is the consequence of Fermat's principle, which in its elementary form states that light ray follows a path that requires the least amount of time to connect two separate points. For instance, a ray that connects point-source with its conjugate point (focus) formed by a positive lens will follow different paths, depending on its initial orientation. A ray arriving at the front lens surface along the path coinciding with its optical axis, will proceed straight toward the focus. On the other hand, a ray arriving at the front lens surface at an angle, will bend (refract) entering the lens, according to the law of refraction, reach the opposite lens surface along the straight line, refract again when exiting the lens, and arrive at its intersection with the chief ray (i.e. Gaussian image point) following a straight line.
Whether the point of intersection of all
the rays will coincide with the lens focus, is determined by the optical
properties of the lens. In order for that to happen,
optical path length for all rays needs
to remain constant. Note that optical path length differs from path's
geometric length, being subject to the media refractive index: optical
path length through a media of refractive index 2 is, for instance,
twice its geometric length. This is why rays having different geometric
path lengths traveling through a lens objective, still can have
identical optical path lengths, enabling wave points in phase to arrive
at the focal point simultaneously. Variations in optical path length of individual rays, on the other hand, result in optical path difference for wave points in phase, wavefront deformation, and wave phase mismatch at the focal point. While optical path length and optical path difference resulting from it are obtained from the geometry of rays in a given optical system, the focal zone ray geometry alone is not directly related to these categories, hence it is not a reliable predictor of the level of optical quality. Ray aberrations are merely linear ray deviations from the focus point, thus not conveying any information on the actual energy distribution around it. Yet, ray geometry offers convenient way for determining basic properties of an optical system. Gaussian, or "paraxial" approximation, introduced by Carl Friedrich Gauss, follows rays close enough to the axis that sines and tangents can be replaced by the angles themselves; this is so called "first-order" optics, used to determine paraxial focus location. Gaussian focus coincides with the focus of a perfect optical surface, or system. On the other hand, best or diffraction focus is the location of best actual image, which is in the presence of aberrations often displaced from Gaussian focus.
Transverse ray aberrations can be presented graphically by plotting points of intersection of a selected number of rays with the focal plane. These are referred to as ray spot or ray spot plot (FIG. 22, center) also, ray spot diagram, or geometric blur. Another form of presenting transverse ray aberration is ray fan plot (FIG. 22, left); similarly, longitudinal aberration can be plotted as a function of the ray height in the pupil (FIG. 22, right). Transverse ray deviations can be expressed in angular form, given by the size of transverse aberration relative to the system focal length.
As already mentioned, ray aberrations are not reliable indicator of energy re-distribution within diffraction pattern, which is the key information needed to access the effect of aberration on image quality. There is simply no direct relation between either geometric or angular form of ray aberrations with the physical aspect of imaging - that is, wave interference. However, they can give a rough impression of imaging quality and, when resulting from known forms of wavefront aberrations, their relation to the RMS wavefront error is also known and, thus, can be associated with a specific degree of image deterioration.
A more recent
form of the geometric blur presentation, the RMS
spot size, gives statistical spot size expressing average
distance of a large number of individual rays from the central spot,
according to Rrms=(Ax+Ay)1/2,
where A is the averaged squared spot deviation in x and
y direction from central point. It
is not to be confused with the RMS wavefront error, a much more accurate
indicator of optical quality. While the RMS spot size is probably
somewhat less uncertain as an optical quality indicator than a plain geometric blur size, it is still mainly determined by the
geometric blur size, hence not significantly more reliable. For
instance, geometric blur size for paraxial, marginal and best focus for
spherical aberrations relate as 1:0.385:0.5, respectively; their RMS
spot sizes relate (in the same relative units) as 0.5:0.289:0.204, while
the respective RMS wavefront errors relate as 1:1:0.25. It can be
helpful in converting ray spot plots of different shapes and
distributions to a circle radius, hence making them comparable in
that respect.
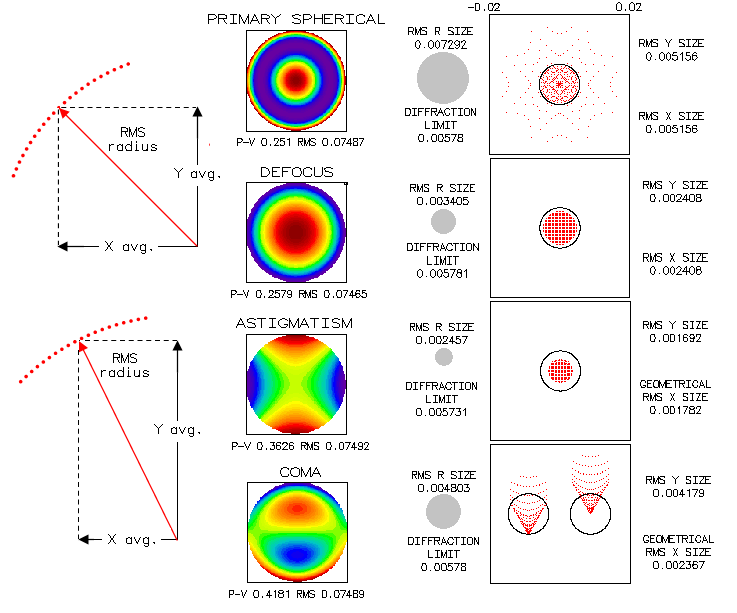
As shown below, discrepancy between the RMS spot size for different
aberrations of the same magnitude is just as large as for the standard
ray spot plot. At left is the schematics of the RMS spot components
for rotationally symmetrical (top) and asymmetrical (bottom) aberrations.
The "diffraction limit" is the Airy disc radius (586nm wavelength),
and the "RMS R size" is the RMS spot radius.
All aberrations are shown at the level of 0.80 Strehl, for an f/8 system.
Yet the RMS spot size varies threefold. Note that all spots have
for the reference center image centroid, which for rotationally symmetrical spots
coincides with the chief ray point of intersection with image surface,
but for asymmetrical spots, such as coma spot (centroid-centered left,
chief ray centered, right), does not.
Directly related to the RMS spot size is
geometric PSF (Point Spread
Function), determined by the distribution of rays in the image plane, so
called ray or geometric irradiance (as opposed to actual
energy distribution given by
diffraction PSF). The point around
which the rays are balanced quantitatively is called centroid
(center of gravity). For radially symmetrical aberrations like
spherical, or those with a central symmetry, like astigmatism, it
coincides with the position of the chief (central) ray; for asymmetric
aberrations, such as coma, it is shifted from it according to the form
of ray distribution.
|
Linear ray deviation from the focus
point has two forms: longitudinal, measured along the chief (central)
ray, from where it intersects with aberrated ray to the focus location,
and transverse, measured from the focal point to the ray height above or
below it in the focal plane. The former defines
longitudinal ray aberration, and the latter
transverse ray aberration (FIG.
22,
center).
As an initial indicator of optical quality, optical designers often
consider a system close to "diffraction-limited" if its ray spot radius
doesn't exceed the Airy disc radius. Called the
Golden rule of optical design, it is still a very loose
indicator of optical quality which, depending on the type of aberration,
can be associated with aberration 