|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
1.3.1.
Gaussian approximation

In the paraxial, or Gaussian approximation,
the image of a point is assumed to be formed by the rays close to
optical axis - paraxial rays - for which sine of the angle practically equals the angle
itself (in radians). Replacing sine by the angle simplifies the
expressions for refraction and reflection (Snell's
law), allowing for quick, yet
accurate assessment of basic spatial and geometric image properties,
derived from the pupil-to-image separation. Since it effectively uses
only a small central portion of the optical surface, it does not provide
information on image quality, i.e. aberrations. In aberration-free
systems, Gaussian and actual focus coincide.
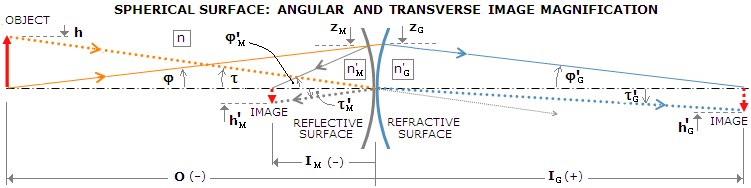
Image separation for an imaging surface, refracting or reflecting, is obtained from this basic equation relating object
distance O, single optical surface radius of curvature R
and image-to-surface separation I:
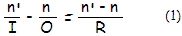
with n
and n'
being the refractive index before and after reflection
or refraction, respectively. This gives the image separation I=n'RO/[(n'-n)O+nR]. In other words, n is the index of
incident medium, and n' is index of the refractive or reflective
medium. Numerically, either is positive for light traveling from left to right, and
negative for the opposite direction (also, according to the
sign convention,
object or image distance is negative when either is to the left of surface,
positive when to the right).
For a given surface radius
R, image and object distance are in inverse relation; the image
of farther away objects is closer to the objective. As the object
distance O approaches infinity, image distance I reduces to the focal
length I=R/[1-(n/n')]=f.
The focal point is called paraxial, or
Gaussian focus.
This relation is derived from the geometry of refracting (or reflecting)
ray, illustrated below, for reflecting and refracting surface of
similar radius of curvature (FIG. 9).

FIGURE 9: The geometry of refraction/reflection leading into the
fundamental relation of Gaussian approximation (all angles are
exaggerated for clarity). O and I
are object and image distance, respectively, n and n' are
index of refraction before and after refraction/reflection,
respectively, and R is surface radius of curvature;
φ is field angle,
α
is angle of incidence to surface normal,
δ
is angle of normal to the axis,
α' is angle to the surface
normal of refracted/reflected ray and
φ' is angle of
refracted/reflected ray to the axis.
The subscripts G
and M are for "mirror" and "glass",
respectively.
In paraxial approximation,
angles are small enough that their sines correlate as the angles
themselves. Thus the Snell law of refraction, nsinα=n'sinα'
simplifies to nα=n'α',
leading to the equality δ=φ-α=φ'-α',
with δ
being the angle between the surface normal and the axis,
φ,
α
the incident ray angle with the axis and surface normal,
respectively, and φ',
α'
the angle of refracted/reflected ray to the axis and normal,
respectively (according to the sign convention, αM, δG
and φ'G
are numerically negative; applying sign convention makes possible to use
the same relations for both, reflection and refraction). With
α=φ-δ and α'=φ'-δ, substituting into the simplified
Snell's law gives n(φ-δ)=n'(φ'-δ)=n'φ-nδ=(n'-n)δ
which, after replacing the angles with the appropriate height/distance
ratio (φ=h/O,
δ=h/R and
φ'=h/I, with the common ray height h at the
surface cancelling out), leads into Eq. 1.
Similar scheme can illustrate what
defines magnification of the image formed by an optical surface.
Transverse
magnification MT
of the image formed by optical surface is given as a ratio of the image
vs. object height, MT=h'/h.
With h=Iτ',
where I is the image separation and
τ'
the refracted/reflected angle, and h=Oτ,
where O is the object separation and
τ
the angle of incidence, MT=Iτ'/Oτ.
Since, according to the Snell's low, in paraxial approximation
τ'=(n/n')τ,
with n and n' being the refractive index of incident and
transmitting media, respectively, transverse image magnification can be
written as
MT=nI/n'O.
Since O, I and n'
are numerically negative for mirror surface, and
O is numerically negative for refractive surface, transverse
magnification is for both numerically negative, i.e. image orientation
is opposite to that of the object. As before, parameters related to the
reflected ray have subscript M
(for mirror) and those related to the refracted ray subscript
G (for glass); the
illustration assumes common scenario where either surface is in air
(n=1).
Angular magnification MA
is defined as a ratio of the angle between axis and a ray connecting the
axial object and image point through a given surface zonal height z,
the angle at the image vs. angle at the object, or MA=φ'/φ.
With φ=z/O and φ'=z/I, it can be written
as MA=O/I.
Hence, MTMA=n/n'
and, substituting
MT=h'/h
and
MA=φ'/φ,
gives n'h'φ'=nhφ. In other words, change
of these three parameters in the transmitting vs. incident medium offset
one another, and the quantity nhφ, called Lagrange
invariant, doesn't change with reflection/refraction.
Gaussian approximation is strictly valid only for rays close to the optical axis - paraxial
rays - and used to determine their points of convergence. In principle,
these points coincide with the points of convergence of a perfect
(aberration-free) system. While Gaussian approximation does not provide
direct information about image aberrations, it is a quick, practical way
of determining location of the paraxial focus of an optical surface, or
element.
For thin lens in air, first surface
indici are n=1
for light traveling from left to right, and n'=nG,
nG
being the glass refractive index, so Eq. 1 applied to
the first surface becomes
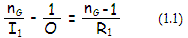
I1
being the front surface to (its) image separation, and R1
being the front surface radius of curvature. For a very distant object,
1/O is infinitely small, and its image forms at a distance I1=nR1/(n-1)
from the first surface. This is now the object distance O for the
second surface (n=nG
and n'=1),
which will form the final image at a distance I2,
equal to the lens'
focal length fl according to (1/I2)=1/f=[(nG-1)/R1]-(nG-1)/R2,
which comes to:
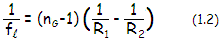
This expression
is referred to as thin lens equation, or
lensmaker's formula. It can be also written
without inverted radii as
fl=R1R2/(nG-1)(R2-R1).
Note that in the standard right-hand
Cartesian coordinate
system distances to the left are negative, and those to the right
positive; consequently, biconvex lens has the front radius positive and
the rear radius negative.
This
implies that the focal length of thin lens equals lens-to-image
distance with object at infinity, i.e. far enough that the rays coming
from it are practically parallel. Based on these same principles, with
the object for the rear lens being the virtual image formed by the front
lens, focal length fC
of two thin lenses in contact, in terms of their focal lengths f1
and f2
is:
1/fC
= (1/f1)
+ (1/f2)
(1.2.1)
The
relation is still valid for two thin lenses separated by a small
air-space, For all practical purposes, it also applies to a cemented
lens (with f1
and f2
being the respective focal lengths in air), since
the effect of denser exit media for the front lens is, for all practical
purposes, offset by the denser incident media for the rear lens.
Likewise, for two thin lenses at a separation L, image forms at
an effective distance (measured from the rear lens) I=(Lf2-xf1f2)/(L-xf1f2),
where x=O/(O-fC).
For large object distance O, x=1
and I=fb,
with fb
being, as before, the back focal length, i.e.
the rear-lens-to-image separation:
fb
= (Lf2-f1f2)/(L-f1-f2)
(1.2.2)
The corresponding combined focal length is determined by the point of
intersection between the marginal ray of axial cone converging toward
focal point extended backward to a parallel-to-optical-axis line
drawn from the end point of the front lens aperture, i.e. it is larger
than the back focal length by a factor 1/[1-(L/f1)].
Mirror focal length fm,
after substituting n=1
and n'=-1
(for incident light traveling from left to right, according to the
sign
convention) in Eq. 1, resulting in (1/I)=-2/R=1/fm,
is defined as:
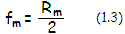
with Rm
being the mirror radius of curvature. According to the sign convention,
both, mirror radius of curvature and its focal length are numerically
negative. While it is usually applied to the radius, mirror focal length
is often given positive, for practical reasons.
Relation between object distance O,
image separation I and objective's focal length
f can be expressed in a general form given by
the Gaussian lens formula as:
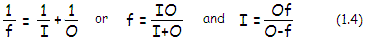
For thin lens, the sign is positive for real object, image and focal
length, and negative when they are virtual. It is also valid for mirrors and objectives in general, under the
same assumption that object distance and focal length of a converging
cone are both numerically positive, with image separation being
determined according to their specific values (positive for O>f,
negative - indicating diverging imaging cone - for O<f). This is not
necessarily in
accordance with every sign convention, but is used for convenience when
finding these distances is the sole purpose of calculation.
For very distant objects, 1/O
approaches zero, and O/(I+O) approaches 1, with the focal length f and image separation I
practically coinciding. Evidently, the relation directly implies
that the closer the object, the farther from the objective its
image.
In this, form, however, the relation is not generally applicable; for
instance, a concave mirror surface oriented to left forms the real image, but
its image separation and focal length (for object at infinity) are also
measured from right to left, thus numerically negative in the standard
coordinate system. Likewise, object distance, if measured from the
aperture stop is also numerically negative. In order to make this
expression generally applicable, and useable in chosen
sign convention, it needs to be
modified to:
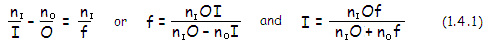
with nO
and nI
being the refractive index of object and image space, respectively.
For lens, nO=nI=1,
and for mirror nO=1
and nI=-1;
image separation I is positive for the former, negative for
the latter. Object distance O is negative for both.
As noted, both above expressions apply when the
imaging medium is air, a common circumstance. In general, focal length is,
from Eq. 1.4, defined by f=nIO/(I+O), with n being the
refractive index of the imaging medium. Hence, nominal focal
length increases with the medium refractive index. However, due to the
change in the effective wavelength - which compresses inside denser media, and
vice versa, resulting in the correspondingly smaller diffraction pattern,
the effective focal length remains identical to that in air, i.e.
smaller by a factor of n (an example being the optical system of
human eye).
From Eq. 1, paraxial image distance formed by a
single refractive or reflective surface of radius R, for object space
refractive index n and image space refractive index n' is
I=n'/[(n/O)+(n'-n)/R]. For lens in collimated light, n/O is zero for
the first surface, and image formed by it effectively becomes object for
the second surface, with the latter forming the final image if this
object at the distance equaling focal length. Denoting refractive indici
from the object space to the image space as n1,
n1'
(at the front lens' surface) and n2,
n2'
(at the rear surface), the focal length is given by f=n2'/{[(n2'-n2)/R2]+(n1'-n1)n1/n1'R1},
with R1
and R2
being the front and rear surface radius of curvature, respectively.
Alternately, it can be expressed as a complete (thick
lens) formula, for n0,
n1,
n2
being the refractive index of object space, lens and image space,
respectively, 1/f=[(n1-n0)/n2R1]-(n1-n2)/(n2R2)[1-(n1-n0)t/n1R1],
where t is the lens axial thickness. For relatively small t,
analogously to lens immersed in air, it simplifies to the thin lens
formula, 1/f=[(n1-n0)/n2R1]-(n1-n2)/n2R2.
Illustration of the basic geometry
of image formation is given on FIG. 10. From the geometry of
either thin lens or mirror, image vs. object transverse magnification
M=hI/hO=I/O,
with I, O being, as before, image and object distance,
respectively.
 
FIGURE 10: Geometry of image
formation by thin lens (A) and mirror
(B)
in air.
Incident ray parallel to the optical axis (2) is directed,
after reflection or refraction, to the focal point F, located
at its intersection with the optical axis. It determines the focal
length
f. Incident ray 3 coming from the same object point
through the front focus F' or F refracts or
reflects parallel to the optical axis; its intersection with ray 2
determines the image point location. Alternatively, it is also
determined by the point of intersection with the incident ray
arriving at the center of the objective (1, the chief
ray). As object distance increases, incident rays coming through
the front focus and center of the objective (3 and 1, respectively)
merge closer, practically merging together for
very distant objects. At that point, image magnification, given as
image-to-object-distance ratio, approaches zero
- with the field angle
α
reduced to
a very small, but finite quantity - and the image practically forms
in the focal
plane. The height hi
of the point-image of a point-object producing an oblique incoming
pencil is a product of the incoming angle a and lens-to-image
separation, hence for any given angle proportional to lens-to-image
separation.
Inset at top left in (A) shows formation of virtual image;
unlike real image, which is formed by converging rays, virtual image
is formed by projecting diverging rays in opposite direction. Shown
is virtual image of the object inside lens' focal length; unlike
real image, virtual image is erect and on the same side as the
object. Bringing object still closer results in its virtual image
shift toward it, with the two coinciding for the object at the
surface. Virtual image is also formed by a negative lens and object
farther than its focal length from it. In the presence of an optical
surface, or element, following the surface/element producing virtual
image, such image becomes its virtual object .
When the lens thickness is significant with respect to
the object distance and focal length, the ray path through the lens
becomes a factor in determining lens' focal length
f, and needs to be taken into
account (C).
Here, focal length equals the separation between 2nd principal
plane - a plane normal to the axis, containing the point of
intersection (principal point P2)
of extended path of a collimated incident ray and reversed path of
it after exiting the lens - and the focal point (F'). It is
preceded by the 1st principal plane, determined in the same manner
with collimated incident ray from the opposite direction (principal
point P1).
The corresponding points on the two principal planes are always at
the same separation from axis, i.e. lay on a line parallel to it; in
effect, all rays refracted by a lens behave as if the only
refraction is taking place at the principal plane. A ray whose
incident and final orientation doesn't change (in other words, its
path before and after lens are parallel) determines lens' nodal
points. For a single lens, nodal points lay in the principal
planes, 1st nodal point (N) in the 1st principal plane, and
2nd nodal point (N') in the 2nd principal plane. Principal planes are not necessarily contained within lens, and may
be located at a significant distance from it (for instance, with
Maksutov corrector). Also, in unequifocal lenses or systems, such as
human eye, with different incident and final medium refractive index
(thus different focal lengths in these respective media), nodal
points are displaced axially from the principal planes, although the
nodal points separation remains identical to that of the principal
planes, Note that the above scheme is a paraxial (Gaussian)
idealization, ignoring lens' aberrations, thus only valid for
paraxial rays.
The three pairs of points illustrated on
FIG. 10 - object space and image space focal point (F and
F'), 1st and 2nd principal plane points (P1,
P2)
and 1st and 2nd nodal point (N, N') are called
six
cardinal points of a lens or imaging system. These points describe
its Gaussian imaging. For thin lens, or mirror, a single cardinal point
- the focal point - suffice. Thick lens also requires specified
principal planes, and systems where nodal point are not contained in the
principal plane, require in addition specified nodal points, for
determining the angle between object point and the corresponding image
point (axis of object orientation, such as visual axis of human eye), as
well as the image space focal point.
◄
1.3.
Optical system of a telescope
▐
2. MAIN FUNCTIONS OF A TELESCOPE
►
Home
| Comments |