|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS ◄ 1.4.1. Gaussian approximation ▐ 2.2. Telescope resolution ►2. TELESCOPE FUNCTIONSThe main purpose of astronomical telescope is to make objects from outer space appear as bright, contrasty and large as possible. That defines its three main function: light gathering, resolution and magnification. These are the measure of its efficiency. All three are related to some extent, but also have their individual characteristics and limits. 2.1. Light gathering powerLight-gathering power of a telescope mainly depends on its aperture diameter. However, it is the system light transmission that determines how much of the light that entered the telescope actually arrives at the final focus. Transmission losses occur due to reflection, scattering and absorption of light, as well as due to obstructions and diaphragms in the light path. Aperture directly determines how much of the light from distant objects is captured. Therefore, light-gathering gain of a telescope vs. naked eye is primarily due to its larger aperture. The naked eye pupil opening, at its widest, ranges anywhere from ~4mm to ~8mm in diameter, with 6mm being the most often cited average. Thus - neglecting for the moment transmission and possible obstructions - telescope of aperture D in mm will gather (D/6)2 times more light than the average night adopted eye. How much of this light reaches the eye will depend on telescope's light transmission efficiency. Transmission losses at mirror surface range from ~2% to ~20%, or more, depending on the type and state of the coating, as well as the wavelength of light. For fresh aluminum coating, reflection loss for the peak visible spectrum is ~10%, which can be nearly cut in half with a special, or "enhanced" aluminum. Dielectric reflective coatings can reduce the loss to a fraction of a percent (silver coating has somewhat better reflectance for wavelengths above 500nm, and somewhat inferior below 500nm, but it is unstable and quickly deteriorates; it is also more expensive).
r=[(nicosαi-ncosα)/(nicosαi+ncosα)]2, where ni, n are the refractive index for incident and refractive medium, and αi and α are the incident and refracted angle. For lens in air and small incidence/refraction angles, common with telescope objectives, it reduces to r=[(n-1)/(n+1)]2, n being the glass index of refraction. It is shown on the left for 1≤n≤2. However, even simple anti-reflection coating, such as MgFl (magnesium fluoride), reduces reflectivity to ~1%, and more advanced coatings have it nearly eliminated. Nothing can be done about in-glass light absorption; it is at ~4% per inch of in-glass light travel for the typical optical crown, and somewhat more for typical flint, averaged over the entire visual range (400nm-700nm). For a narrower range, of high spectral sensitivity, absorption figure is probably 1-2% per inch (standard, including higher grades, do not come supplied with the absorption figure, it is only given for a small "typical" samples of unspecified quality). It can be below 1% for highly purified, high-grade glasses, but for some glasses it can be significantly larger, either due to their lower purity (grade), or their inherent composition. Losses due to in-glass absorption are roughly doubled in the blue/violet part of visible spectrum, compared to the green/red. Light loss in glass elements, therefore, increases with the number of uncoated surfaces and the in-glass path length. For uncoated doublet objective, it is about 15% due to reflections, plus nearly 0.5% per inch of aperture due to in-glass absorption. For coated doublets, it is about 4% plus the absorption loss. The eyepieces are these days usually multicoated and, unless of exceptional size, have up to a few percent total light loss. Finally, most reflecting telescopes have central portion of their main mirror obscured by a smaller secondary mirror - so called central obstruction. Size of central obstruction is usually between ~0.15D to ~0.4D, resulting in ~2% -16% light loss. The true light-gathering power of a telescope is given by the product of its aperture area and transmission coefficient. At a rough average, light transmission is about 80% for amateur telescopes, although there are systems as low as ~60%, and those as high as ~95%.
Based on the original concept by Hipparchus, who classified all naked eye stars into 6 size (i.e. magnitude) categories, with the brightest being assigned 1, the larger nominal magnitude, the fainter star. It was Norman Pogson, in 1856, who established the exact numerical relationship between apparent stellar brightness and magnitude as m=-1000.2log10L+constant, with L being the star luminosity. The logarithmic form reflects nearly logarithmic physiological response of the eye to variations in the light intensity level (i.e. eye perceives the relative change in light intensity l=L2/L1 as 1+log10 l), with visual magnitude being, in effect, the logarithm (exponent) to the base 1000.2. In other words, a 100 times brighter 1st magnitude star appears to the eye as being only 5 times (magnitudes) brighter than a 6th magnitude star. A simpler relation
expressing the basic brightness/magnitude
relationship (i.e. 5 magnitudes equaling 100 times brightness
difference), log In more practical form, stellar luminosity is expressed as a relative number; for instance, a star that is 10 times more luminous than a reference star of magnitude m0 (usually magnitude 0 star), will have the magnitude m=m0-2.5log1010=m0-2.5. If it is 1/10 as bright, its magnitude is m=m0-2.5log100.1=m0+2.5. Or, in its general form, m=m0-2.5log10(L/L0). Similarly, two unresolved stars of apparent magnitudes m' and m", will have the combined magnitude m=m'-2.5log10[1+2.5(m'-m")]. By replacing L/L0 with (D/E)2, where D is the aperture diameter and E the eye pupil diameter, we come to the relation for the limiting magnitude of a telescope, based on its nominal light-gathering power, given as its aperture area vs. pupil area, as mL ~ me+ 5log10(D√T/E) (2) with τ being the telescope's light transmission coefficient (0 to 1), me the naked eye limiting magnitude corresponding to eye pupil diameter E (both in the same linear units). This is the basic approximation for the limiting telescopic magnitude, which only factors in aperture differential and transmission, assuming background brightness nearly identical for both, naked eye and telescopic image. That is, with the eye pupil diameter nearly equaling the telescope (eyepiece) exit pupil diameter X, or X~E (assuming only a minor light transmission loss). Table below gives limiting magnitudes for a few selected apertures and transmission coefficients, based on this relation.
The night-time eye pupil diameter is for most people between 5 and 7mm, but it doesn't affect limiting telescopic magnitude, since the gain or loss in the naked eye limiting magnitude is offset in the telescopic gain. A simple relation for the magnitude gain or loss Δm, based on light-gathering ratio β between two apertures, is given by: Δm = 2.5log 10β (2.1)So, if the naked eye limiting magnitude is, say, 5, a telescope collecting 100 times more light (l=100) will gain Δm=2.5log10100, or 5 magnitudes, for the corresponding limiting magnitude of 10. However, actual limiting magnitude achievable is up to four magnitudes, or so, higher than what is implied by Eq. (2), mostly due to darkening of the background at high magnifications, moments of exceptional seeing and use of averted vision. Gain in the limiting magnitude due to magnification factor - with the sky background being approximately as bright in a telescope with the exit pupil equaling eye pupil - can be approximated by log10(E/X)2. Thus, a more complete formula for the limiting magnitude of a telescope can be written as: mL ~ me+ 5log10(D√T/E) + 2log10(E/X) (2.2) Obviously, for E=X the limiting magnitude is identical to that given by Eq. 2. Following table gives limiting stellar magnitudes for the the same apertures, for low, medium and high magnification.
And graph below gives more complete picture of the dependence between limiting telescopic magnitude and telescope magnification, defined with the ratio between eye pupil corresponding to the naked eye limiting magnitude and telescope exit pupil (which, being proportional to telescope's relative magnification, indicates change in background brightness). The blue plot is based on relation (2), which effectively assumes constant background brightness, and the top tree plots are for E/X ratios 2, 4 and 10, which correspond to relative magnifications 0.4, 0.8 and 2 in units of aperture diameter in mm (from the nominal magnification M=D/X, or 1/X in units of aperture, X being the exit pupil diameter, which after substituting X=E/ratio gives relative magnification as ratio/E; for the naked eye exit pupil diameter E in inches, the relative magnifications in units of aperture are larger by a factor of 25.4, i.e. 10, 20 and 50).
While the apparent sky background brightness is inversely proportional to (E/X)2, field tests show that the resulting limiting magnitude gain or loss changes at a significantly slower rate. The rate is also faster for bright background, when gain in limiting magnitude can approach half of the nominal change (darkening) of the background within a range of several magnitudes. With dark sky background, the gain can be less than half as much for the same nominal change in background brightness (most of this effect is likely caused by the background brightness falling below perception threshold of the eye). This implies that higher magnification mainly compensates for the limiting magnitude loss due to light-polluted sky.
Other factors also influence limiting magnitude of the telescope, but their significance is relatively small. Eye transmittance directly affects the naked eye limiting magnitude value, and insomuch the limiting magnitude in a telescope. As the eye light transmittance graph implies, average eye transmittance over the visual range varies between 40% and 90% (approximately). Thus, in otherwise identical conditions, it can vary up to 0.9 magnitudes - possibly more - from one individual to another. In other words, what is, say, 5-magnitude sky for you, may be slightly better than 4-magnitude sky for someone else - or the other way around. This assumes identical pupil opening; different pupil size will either increase or reduce the difference in perceived brightness due to transmission. Consequently, limiting magnitude of a particular telescope will also vary up to a magnitude, or more, from one individual to another. Stellar magnitude is the basis for integrated magnitude, which represents total brightness over an area expressed in terms of stellar magnitude. Thus, for given magnitude, an extended object is always fainter than a star (that is, with lower surface brightness), and limiting magnitude for extended objects is generally brighter than limiting stellar magnitude (it also varies depending on the intensity distribution over the object). Considering that surface brightness of the telescopic image diminishes with the square of magnification, it is always lower - at least for the transmission loss at the minimum useful magnification, and more at higher magnifications - in the image seen through a telescope, than in the image seen by the naked eye. However, telescopic image on the retina is much larger, and the total of light energy - or total brightness - much higher. That is why the Moon appears so much brighter in a telescope, despite its surface brightness being normally (due to magnification) much lower. ◄ 1.4.1. Gaussian approximation ▐ 2.2. Telescope resolution ►
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
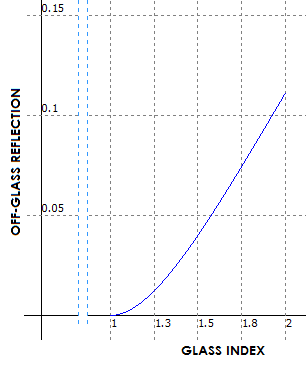Lens elements lose light due to reflection from lens surface
and absorption by the glass. Reflection from uncoated lens surface is
~4% for typical glasses and near-normal incidence. Specifically,
reflectance at the boundary of two transparent media is given by
Fresnel's formula:
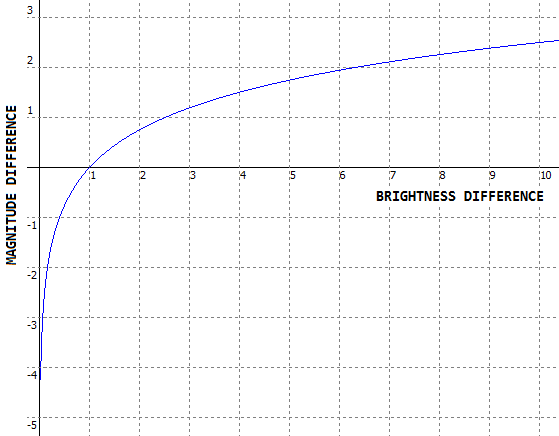Light-gathering power of a telescope is often
expressed in terms of limiting stellar magnitude detectable.
The apparent stellar magnitude - usually denoted by m - is a measure of apparent brightness, with a
5-magnitude difference representing 100 times brightness difference; thus
the difference in one magnitude implies difference in brightness of
2.512 (from 100
L=2.5log
Both, telescopic and naked eye limiting magnitude are affected by atmospheric absorption. It is on average
0.25m at zenith, and increases approximately with 0.17z/(90-z) in
magnitudes, z being the zenith distance in degrees (based on the
graph in Sidgwick's Amateur Astronomer's Handbook, p449).
Limiting magnitude around zenith is, on average, over 1 magnitude
fainter
than close to horizon. Graph at left shows the approximate change in absorption with zenith angle for selected wavelengths spanning the visual range (h, g, F, e, C and r spectral lines correspond to 406, 436, 486, 546, 656 and 707nm wavelength, respectively).