13.7. COMBINED EYE ABERRATIONS, DIFFRACTION, RAYTRACING EYE MODEL

In any optical system, the effect of wavefront aberrations - either those induced by the eye itself, by the optical train of a telescope, or externally - is adding to the effect of diffraction in further spreading out the energy making up the point-image. Eye is not an exception. At small pupil sizes, eye diffraction is the main determinant of image quality; at large pupil sizes, that role belongs to eye aberrations, and at intermediate pupil sizes, both diffraction and aberrations are significant factors.

Not surprisingly, studies give different indications of the maximum average pupil size at which the eye is still diffraction-limited (0.80 Strehl, or better). The range spans from 1.22mm diameter, or as low as 0.76mm when tilt is excluded (Thibos et al. 2002), to 2.8mm (Howland and Howland, 1977). Prevailing view is that the average eye remains diffraction limited up to about 2mm pupil diameter, after which its exponentially increasing aberrations cause the Strehl to plummet (FIG. 236A). However, the perceived image quality is much less affected than the average nominal Strehl, primarily due to the low effective magnification of the eye (in other words, angular size of either dominant diffraction pattern, or dominant aberrated pattern, remain below detection threshold of the eye).

Size of the geometric aberrated blur (i.e. ray spot size) also varies with the eye model used. There is a number of optical models of the eye, from the simplest one by Emsley (1946), with a single refracting surface on a water-like medium (1.333 refractive index), to a complex system proposed by Liou and Brennan in 1997, incorporating aspheric surfaces and varying refractive indici (the latter is most closely resembling biological eye, and reproducing its aberrations). The plot is based on eye model with physical dimensions of the average eye, constructed to produce its type and level of foveal aberrations. Specs given in table below (surrounding medium for the cornea and lens is water; their dispersive properties are obtained by scaling up those for water approximately corresponding to the change in e-line refractive index).

CORNEA

LENS

R1/aspheric

Thickness/n/V

R2/aspheric

R1/aspheric

Thickness/n/V

R2/aspheric

Tilt

Decenter

7.8mm
-0.25*

0.5mm
1.383/1.380/1.376
62.5/62/61.5

6.5mm
0.145**

10.2mm
0*

3.6mm
1.423/1.420/1.416
65.5/65/64.5

-6mm
-3*

2�

0.2mm

R=radius of curvature; n=F/e/C refractive index; V=F/e/C Abbe number; *conic; **toric curvature

As presented previously, both monochromatic and chromatic foveal aberrations are nominally significant at medium to large eye pupils. Their combined and separate effects are best illustrated on MTF graph (FIG. 236B). Same goes for monochromatic aberrations - which are usually the primary concern - and their dependence on the pupil size (FIG. 166C,D). The actual size of diffraction pattern, either nearly aberration-free (at small pupil sizes) or heavily aberrated (at large pupil sizes), does not change much going from small to large pupil sizes - certainly much less than the nominal Strehl, or the RMS wavefront error value (FIG. 236E).

FIGURE 236: (A) Generalized scheme of the respective magnitudes of aberration-free (diffraction-limited) and average real (i.e. aberrated) eye, on axis. Geometric blur size and RMS wavefront error have nearly identical rate of change, thus both scales apply to the same plot. With all eye aberrations included, diffraction dominates for pupil diameters smaller than 2mm, about 1.5mm, and for larger pupils eye aberrations. At ~2mm pupil diameter, diffraction blur, conventionally represented by Airy disc or by FWHM, is about 2.4 and 1 arc minute, respectively. For larger pupils, it is enlarged due to eye aberrations, and for smaller pupils due to diffraction. With defocus corrected, which applies to the telescopic eye, eye is diffraction limited for pupils diameters smaller than ~3mm. Relative magnitude of higher-order aberrations increases with the pupil size, becoming comparable to the defocus-corrected eye (i.e. plagued only by primary astigmatism) at pupil diameters over 8mm.
(B) Foveal eye contrast transfer for 5.7mm pupil diameter without correction, with corrected 2nd order aberrations, and with corrected monochromatic aberrations (based on Guirao et al. 2002). The latter effectively shows contrast transfer drop due to eye's chromatic aberrations; at this pupil size, eye chromatism (longitudinal and lateral error combined) cause more contrast loss than secondary spectrum in 200mm f/5 achromat (shown in the corresponding relative range of frequencies). Spatial frequency - given by 1/ν, with the frequency ν determined by the inverse of the wavelength-to-aperture ratio, in radians - is, by default, limited to 60 per degree, i.e. one arc minute, despite the theoretical cutoff frequency being 200 per degree, or 0.3 arc minute (as shown on graph C, this theoretical resolution doesn't materialize, due to the contrast level at these frequencies falling below the minimum required by the eye).
(C) Foveal eye contrast transfer for three different pupil sizes, with 2nd order aberrations - defocus and primary astigmatism - corrected. Since eye defocus error is cancelled out by defocusing the eyepiece, these plots are close to the actual monochromatic (around e-line) contrast transfer for the telescopic eye, with eye astigmatism being relatively insignificant at this error level. The MTF for larger pupil sizes indicates considerably higher cutoff frequencies, but the actual cutoff frequency is similar for all three pupil sizes, being determined by the minimum contrast level required by eye for resolution.
(D) Foveal MTF for the same three pupil sizes with spatial frequency normalized to 1. A comparison with MTF for 24mm Koenig eyepiece for identical exit pupil sizes shows that eye aberrations lower contrast more than the eyepiece aberrations for all three pupil sizes. At 2mm exit pupil diameter, the Koenig is essentially aberration-free on axis, and nearly so even at 4mm exit pupil (with the diameter of eyepiece exit pupil is given by the ratio of eyepiece f.l. and system's focal ratio, these exit pupils correspond to an f/12 and f/6 system, respectively). Since the only axial aberration of an eyepiece is spherical aberration, which increases much faster with the pupil diameter than the astigmatism/coma/spherical/trefoil mix of the eye, its contrast transfer at 6mm exit pupil diameter (i.e. with f/4 system) is comparable to that of the eye with 4mm pupil (C and D based mainly on Liang and Williams 1997 and Thibos et al 2000).
(E) Polychromatic and monochromatic diffraction spots for four eye pupil diameters. At 1mm eye pupil diameter, the two patterns are essentially identical, indicating near-zero eye chromatism; at 2mm, the difference is only slight. At 4 and 6mm, polychromatic pattern becomes noticeably fainter, indicating loss of energy due to chromatic error. Patterns are generated by OSLO, with the eye model specified in above table; real eye pattern at larger pupil sizes - as depicted in the dark circle - commonly shows significant random asymmetry, caused by random local deviations of eye surfaces from the rotationally symmetrical conic surface. Change in nominal size of the conspicuous portion of diffraction blur is much less pronounced than its change relative to the Airy disc for corresponding pupil sizes, shown at right. The blur is relatively large with respect to the cones (~2.3μ-10μ from foveola to the outer retina, respectively) and rods (~2.5μ-5μ), hence with the limiting resolution determined entirely by the blur size.

Eye aberrations lower object-to-image contrast transfer, hence the perceived image quality and resolution limit. Actual effect on image quality, however, depends not only on the wavefront error, but also on the retinal image size (magnification). An aberrated image has to be large enough, angularly, to allow the eye to detect the aberration. Average eye begins to recognize image shape, as its size exceeds ~3 arc minutes. Any detail below that size appears point-like to the eye. Consequently, in order for the eye to discern the effect of wavefront aberrations in the retinal image - whether an extended detail or a point-object image - has to be larger than ~3 arc minutes.

That is why the edge-field coma in an f/6 paraboloid is so inconspicuous; at 15mm off-axis, with the coma wavefront error at 2.5 waves P-V (0.45 wave RMS), the sagittal blur size produced by a 25mm eyepiece is still only 3.6 arc minutes on the retina. It takes the blur size of ~5 arc minutes in diameter for the average eye to clearly recognize that it is not point-like; in this case, it would take ~f/5 paraboloid. Considering that the astigmatism of standard eyepieces usually adds significantly to the blur size that far off axis, 5 arc minutes blur size is probably still borderline between inconspicuous and obvious level of aberrations for the average observer.

The required minimum spot size for shape recognition is greater for less contrasty details, as well as for those that fall in the low-sensitivity range of eye photoreceptor cells, cones and rods.

A glance at FIG. 236E reveals that despite its very high nominal aberrations, the aberrated diffraction blur of the average eye is still significantly smaller than 5 arc minutes for pupils smaller than about 5mm in diameter, thus with relatively small effect on the perceived image quality. The exception is eye defocus error (assumed corrected in the patterns shown), which is typically by far the largest eye aberration. It often very noticeably degrades quality of the visual image; fortunately, it does not affect the telescope user.

Raytracing eye model

Eye model used here is somewhat different than the one specified above, main difference being in the type of surface misalignment chosen to produce asymmetrical blurs, more alike those of the real eye, with the aberrations magnitude within the average level. The starting point was model from Chen et al. (Development of a human eye model incorporated with intraocular scattering for visual performance assessment, 2012), simplifying the crystaline lens to only two layers, and limiting misalingment tableo only two surfaces. The radii are modified to produce 23mm physical focal length. Due to image being formed in a watery environment with the refractive index n~1.33, the effective focal length is 17.3mm (this is because the waves get compressed, acting as shorter wavelengths by the 1/1.33 ratio, hence forming correspondingly smaller diffraction image; the entire image scales with it). Geometrically, the focal length is determined by the point where cone converging to the focus extended toward the opposite end intersects marginal rays of the pencil entering the cornea. That point is generally slightly inside the eye, thus the focal lenght is a bit shorter than the phisical separation between front surface of the cornea and focus (in this case 24.6mm). The corresponding focal ratio is approximated by f/P, P being the eye pupil diameter and f the focal length, but its exact value is given as the ratio of a diameter of the pencil entering cornea vs. focal length, in general 10-15% smaller. The Petzval radius for this model is -17.8mm, with the radius of a surface approximating retinal wall -12mm. The five wavelengths spanning the visual spectrum are roughly weighted for empirically indicated mesopic sensitivity. Defocus is omitted as it is not a factor for telescopic eye.

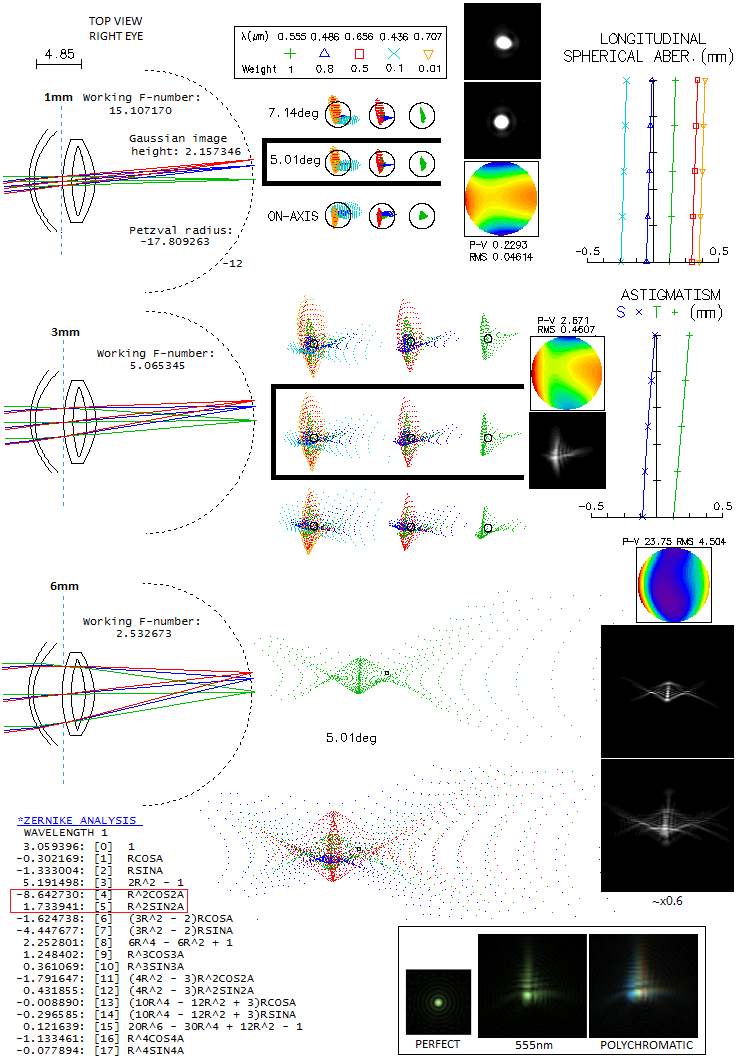
Model is raytraced for three pupil sizes, 1, 3 and 6mm diameter, from top to bottom, with the corresponding pencil diameters at the cornea of 1.14, 3.4 and 6.8mm. The field height of 7.14° is chosen so that the 0.7 field is 5°; this is the angle within 4-8° range, between optical and visual axis of the eye, due to the fovea being that much off the optical axis. Hence, the point that represents image in the center of fovea is that at 5° field (with the 7° is also being within the range). Longitudinal aberrations for axial chromatism and astigmatism don't change with the pupil size. Longitudinal spherical aberration changes (as wavefront error) in proportion to the 4th power of pupil diameter. At the 1mm pupil, spherical aberration is entirely negligible. Dominant aberration is astigmatism, with the longitudinal axial astigmatism of 0.25mm (nearly 1 diopter) implying 0.24 wave P-V, for 555nm wavelength (from LA/8F², LA being the longitudinal aberration and F the focal ratio). Longitudinal chromatism has the form of primary spectrum, with shorter wavelengths focusing closer than longer ones. The error for each wavelength, as P-V wavefront error of defocus, is given with the same formula as for astigmatism, with the only difference being in the wavelength it is measured against. The blue F and red C line have 0.18mm of defocus each, translating to 0.2 and 0.15 wave P-V, respectively. At 0.37mm, the violet g-line comes to 0.47, and red r-line at 0.23mm to 0.18 wave. Diffraction simulation on the bottom shows 555nm wavelenght, and above is the 5-wavelength simulation - closer to what we actually see - showing some deformation due to to the blue/violet being shifted toward their line focus.

At 3mm pupil, f-ratio drops to f/5.1, and both axial astigmatism and chromatism are larger in inverse proportion to the square of it. The eye is already far from "diffraction limited" (0.80 Strehl, i.e. 0.0745 wave RMS). Diffraction pattern (shown for the 5 wavelengths) is up to several Airy discs in diameter, deformed in a more or less asymmetrical blur. At 6mm pupil the focal ratio is only f/2.5 and the blur yet larger - much more vs. Airy disc than vs. blur at 3mm pupil. Diffraction patterns are shown somewhat reduced in size, for 555nm (top) and the 5-wavelengths (bottom). Zernike analysis shows that the primary aberrations are still dominant (not necessarily the case with every individual eye), with astigmatism (4,5) still dominant. Coma (6,7) is roughly half, and spherical aberration (8) one fourth as large (not to forget that these values add up squared, thus coma is actually only one fourth, and spherical aberration one 16th of the astigmatism magnitude). Zernike aberration term value for primary spherical aberration determines the RMS wavefront error when divided by 5^0.5. It gives 1 wave RMS error, i.e. 3.35 wave P-V (spherical aberration becomes obvious on the wavefront map at the minimum RMS error focus, but diminishes to negligible at this focus). That allows to estimate spherical aberration at other pupil diameters, having in mind that it is just a Zernike term, not the actual aberration. For 1mm pupil, it would be smaller by a factor 6⁴, or nearly 1/400 wave P-V. While this is unlikely to be accurate, it is safe to assume that it is at that pupil size entirely negligible. Most of the defocus term (3) comes from manually defocusing from the lowest RMS error focus (3.5 wave) to the focus with the highest energy encircled within Airy disc, and wider. Best focus in this respect (shown) encircles 39% energy within 0.01mm radius, while the lowest RMS-error focus, despite over 20% lower nominal error, only 29%. This illustrates how unreliable the RMS error - together with the Strehl ratio - becomes at large magnitude errors. Emerging higher-order aberrations are trefoil (9,10), secondary astigmatism (11,12) and quadrafoil (16,17).

Diffraction patterns in the box bottom right are from a different eye model. They show one possible blur shape at a mid-size pupil for 555nm wavelength, and for the 5 wavelengths specified above. The colors are there, but brain processing filters them out, and we see a nearly uniform hue over the polychromatic image (on the left is the unaberrated pattern).

In addition to eye aberrations, other important factors determining properties of the image formed by the eye are its spectral response, intensity response, and contrast sensitivity. That comes next.

◄ 13.6. Eye chromatism ▐ 13.8. Eye intensity response ►

Home | Comments