|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS ◄ 13.7. Combined eye aberrations, diffraction ▐ 13.9. Eye spectral response ► 13.8. Eye intensity response, contrast sensitivityEye light-intensity response
PAGE HIGHLIGHTS Human eye is capable of responding to an enormous range of light intensity, exceeding 10 units on logarithmic scale (i.e. minimum-to-maximum intensity variation of over 10-billion-fold). Inevitably, eye response to the signal intensity, which determines its apparent intensity, or brightness, is not linear. That is, it is not determined by the nominal change in physical stimulus (light energy), rather by its change relative to its initial level. In general, there is a minimum required change in signal intensity needed to produce change in sensation, and the latter is not necessarily proportional to the former. It was the father of photometry, Pierre Bouguer, who in 1760 first noted that the threshold visibility of a shadow on illuminated background is not determined by the nominal differential in their illumination level, but on the ratio between the two intensities. In other words, that eye brightness response is not proportional to light's nominal (physical) intensity, but proportional to its intensity level. This threshold ratio, which he found to be 1/64 (around 1.5%) did not change with the change of intensity level. In 1834, German physiologist Ernst H. Weber, based on measurements for a number of different physiological responses, established a general empirical law stating that the minimum noticeable change in input intensity ΔI - so called increment threshold - is in a constant relationship with the intensity level I, i.e.
ΔI/I=constant
(161)
The value of ΔI/I, called Weber fraction, constant, or ratio,
varied with the type of physiological response; for brightness response,
the initial values varied somewhat from one experiment to another (1/64
Bouguer 1760, 1/100 Weber 1834, 1/38 Steinheil 1837, 1/100 Fechner
1858), but it appeared constant, and the value variations were ascribed
to different techniques used and/or to variations in individual
sensitivities. More recent experiments came to the ratio values
specific for the two main types of retinal photoreceptors, ~0.14 and
0.015-0.03 for the cones and rods, respectively (FIG. 237).
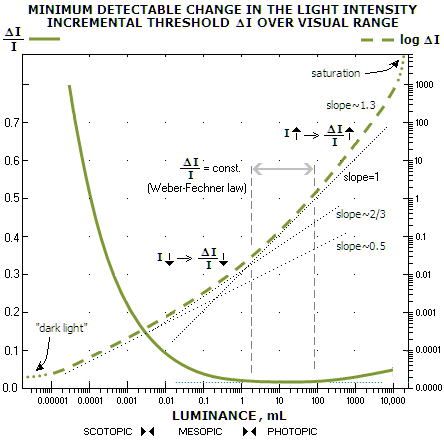
FIGURE 237: If Weber law strictly holds,
brightness increment threshold, either alone or as a ratio vs.
intensity, always changes linearly with the change in intensity. When
both scales of a graph are linear, and the vertical scale is the
increment threshold, the plot vs. intensity has slope equal to Weber
ratio (top left). When both scales are logarithmic, the plot slope
equals 1 (i.e. 45°, top right). With the ratio on the vertical scale,
the plot is always a horizontal line, since the ratio value is a
constant (bottom). As will be addressed ahead, actual data do not
support this simple concept. Similarly, the values found experimentally
are for the specific stimulus/background/ambient forms, and are not
necessarily valid to quantify a general rode/cone response. For
instance, the 0.14 Weber ratio for cones was established based on the
judgment of observers looking at a pair of bright disks briefly flashed
at the same time (Cornsweet and Pinsker, 1965). Just a change in a
single factor - for instance, size of the background relative to the
stimulus - can significantly alter the increment threshold.
Gustav T. Fechner
, German physicist, Weber's student, expanded onto Weber's empirical law:
assuming that just noticeable
difference in sensation
ΔS, corresponding to the
threshold signal change
ΔI, is a unit change in
sensation, defined sensation as S=k(ΔI/I),
where k is numerical constant, an integer. Assuming that for small values of
ΔS and
ΔI, dI/I=dS/k
integrates to
S=klnI+C, with C being an arbitrary constant. This converts
into:
S=2.3klog10I+C
(162)
which is the general form of Fechner's law or, alternately,
Weber-Fechner law. Fechner called it psychophysical law,
believing it applies to all senses (1860). The choice of integer k
affects shape of the curve, which becomes more open (i.e. less steep for
small values of I, and steeper for larger I values) as
k increases. The choice of C merely affects plot's vertical
position.
In its basic form (Weber law), this implies that eye response to
object luminance, as brightness discrimination, is not proportional to
its actual (physical) intensity level; rather, that it changes with the
intensity level, remaining nearly constant relative to it. This, in
turn, under assumption that the relative value of just noticeable
difference in brightness sensation is a unit of the sensation change, means that the perceived object brightness changes with the
logarithm of object's actual brightness.
Fechner was aware that empirical data does not support this simple
concept as a general law. But he diminished the magnitude of
discrepancy, hypothesizing that it becomes significant only at the
extremes of perceived brightness, due to the retinal signal noise: the
lowest neural noise level (dark light) at the low end, and
saturation at the high end. In order to account for the former, he
modified the law into S=kΔI/(I+I0),
with I0
being the neural noise level at near-zero illumination.
However, in 1924 Selig Hecht pointed out
that empirical data clearly indicates that eye brightness response
does not follow Weber-Fechner law over significant portion of its
response range (FIG. 238).
FIGURE 238: The solid blue line tightly fits the
experimental data by Aubert (1865), Koenig and Brodhun (1889) and
Blanchard (1918). It indicates that the Weber-Fechner law - according to
which the smallest perceptible change in intensity ΔI
vs. intensity level I
is constant, thus forms a straight horizontal line when plotted over the
range of luminance that the eye can adapt to - applies only to a portion of
eye's photopic response,
approx, 1-100 millilamberts (1mL=10/π
cd/m2).
Since the luminance is on a log scale, the plot is greatly
compressed horizontally, resulting in an upward swing of ΔI/I
toward mesopic and, particularly,
scotopic illumination level.
Actual nominal value of ΔI
diminishes with the illumination level, but at a slower rate than luminance (dashed). When log ΔI
is plotted against log(I), strict adherence to Weber-Fechner law would
require it to form a straight line with the slope 1 (measured as a ratio
of the height of the vertical intercept vs. corresponding length at the
horizontal scale, thus the slope is 1 for a 45° line). As the plot
shows, log(ΔI)
increasingly deviates from research data at very high and, particularly so,
low and very low illumination levels. Only in the 1-100 mL range
(approximately) the plot nearly conforms to the Weber-Fechner law. Note
that the range of intensity is as given by Hecht, with 0.00001 mL at the
low end; more recent sources extend it to 0.000001 mL, for the I
max/I
min
ratio
of about 1010.
Later experiments confirmed this discrepancy. Based on the available
data, Stanley S. Stevens proposed a new general law for human perceptual
response, in the form S=kIa,
where k is an arbitrary constant and a the exponent
(power). Change in the intercept k affects plot height height in
a coordinate system, thus changes with the choice of unit for I
and/or S; it also changes with the adaptation level (i.e.
luminance intensity level). The exponent a equals the plot's
slope on log-log coordinates.
The log-log plot on FIG. 238 indicates that between the two
extremes - dark light (neural noise preventing any change in the
sensation at retinal illuminations below certain level) at the
rods
threshold, and saturation at the cone limit - there are approximately
four different sub-ranges, each with somewhat different response
function of the general form S=kIa.
For the scotopic range, the exponent a~0.5, thus the smallest
perceptible change in intensity changes with the square root of it.
Throughout mesopic range, a~2/3, while in the photopic range it
gradually shifts from a~1 in its lower portion - where it,
therefore, conforms to the Weber law - to a~1.3 at the higher
luminance levels.
Interestingly, as it was well known to Hecht, the neural response to
light intensity - measured by its photochemical reaction - for the most
part does conform to the Weber law. As an empirical fit to it, he used
the relation CI=x2/(a-x),
with a and x being the concentration of original
photochemical before it reacted with light, and that of photochemical
changed by interaction with light, respectively; C was a
constant, estimated at ~100 for the rods, and ~0.25 for the cones and
I the retinal illumination. Taking a=1, and 0≤x≤1, the relation can
be written as CI=x2/(1-x);
for x as a function of I, it produces sigmoid (S-curve),
with most of its length between the floor (where the curve
asymptotically approaches zero) and ceiling (asymptotically approaching
its maximum, when all of the original photochemical is being converted)
closely enough approximated by a straight line. However, empirical data
clearly indicated that brightness perception does not mirror the
underlying photochemical reaction.
More recently (Rushton and Naka, 1966), a simpler empirical relation was
found to be well approximating the
magnitude of neural response N of both, rods and cones, in terms
of stimulus intensity I and semi-saturating constant σ,
as N=I/(I+σ) which, with steady background I0
added to test stimulus becomes N=σI/(I+σ')σ', with σ'=σ+I0.
The semi-saturating constant σ is the light flash that raises
neural response N to half its maximum value, thus when I=σ,
N=0.5.
Starting with this relation - known as hyperbolic formula, or
H-function - eye brightness response to more complex fields can be
described, and the agreement with experimental data is, as mentioned,
good.
According to Rashton, σ for human rods is about 1,000
quanta (photons) absorbed per rod per flash. The absolute rod threshold
is about 100,000 times smaller, or 1 photon absorbed per 100 rods. This
physiological fact supports Rashton's conclusion that rod response
cannot be explained simply by bleaching of rhodopsin on the rod level,
but that a higher-level processing, such as that at the level of rode community, i.e.
conglomerate of rods, is required. Cone response is similar, only their threshold and
semi-saturating constant are both higher. The multi-level processing of
the light interacting with photoreceptors should, at least in part, help
explain why eye brightness response does not mirror photochemical
reaction at the level of photoreceptor cell.
As noted, graph on FIG. 238 and the corresponding figures are based on older
data, obtained generally by testing the whole eye, with all retinal
photoreceptors actively participating. More recent experiments focused
on determining the isolated response of the specific photoreceptor types
(FIG. 239).
In general, it is considered that cones respond to light in a similar
fashion as rods, only at higher luminance levels. This, however, doesn't
give us a clear picture of what that response is. As the above examples
indicate, eye brightness response is too complex to be accurately
described with a simple concept, such as Weber-Fechner law. At best, it
is applicable to limited sub-ranges of eye brightness response and
some specific stimulus/background forms.
Similar conclusion is suggested for eye brightness response to sine-wave
grating (conventional-MTF-like pattern). Experimental data do not
support the concept of square root law transition from the dark light
level into the Weber law domain (FIG. 239, top). This concept may be relatively
close approximation only for a narrow range of spatial frequencies, but
the model of contrast sensitivity change that fits experimental data best
does not agree with it being generally applicable (FIG. 240).
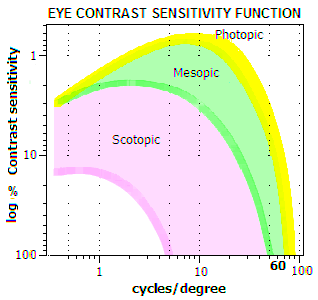
FIGURE 240: Fitting eye contrast sensitivity
function (CSF) into experimental data for sine-wave grating at low
illumination levels, based on DeVries-Rose/Weber concept (top) and the
actual best fit (bottom). Contrast sensitivity scale is in a unit of
(modulation threshold)-1,
with the contrast modulation threshold being 1, or 100% (so, for
instance, contrast sensitivity 100 means that the minimum contrast
detectable by eye is 100-1,
or 1%). TOP: contrast sensitivity
plots satisfying three simultaneous constraints: (1) the empirical
contrast vs. acuity curve, (2) empirical CSF ceiling at 2000 sTd
illuminance, and (3) 0.5 slope CSF (square root law) until it reaches
the CSF ceiling (contrast sensitivity increases with the luminance level
because the increment threshold, according to the square root law,
increases at such rate; after transition into Weber law domain, the
increment threshold remains constant vs. luminance, and the contrast
sensitivity, consequently, remaining unchanged, with zero slope). At
mid-to-higher frequencies (4 and 16 cycles/degree), these plots fall far
short of reaching the empirical CSF ceiling at 2000 cTd. They also
produce discontinuity in the acuity line (sensitivity vs. frequency
projection on 3-D CSF surface), not supported by empirical observations.
BOTTOM: CSF plots that
satisfy the three constraints, and also produce continuous acuity line,
have to be non-linear, of the type shown. For the lowest frequencies,
CSF is nearly stagnant over the range of illuminance, nearly conforming
to Weber law. Over a
very-low-frequency sub-range, CSF has significantly weaker slope than
0.5, while over low frequencies it comes close to the DeVries/Weber law
concept. At mid and high frequencies, however, much steeper slope than
0.5, which agrees with most of the empirical data, and curvilinear plot
are required (Garcia-Perez,
2005).
By its derivation, Stevens' power law is more comprehensive than
Weber-Fechner's law. Like the latter, it starts with the assumption that
ΔI/I=constant=c1,
but expands by assuming that the corresponding smallest noticeable
change in sensation vs. sensation level is also a constant, not
necessarily equal to c1:
or
ΔS/S=constant=c2,
c1≠c2.
Taking c1/c2=a
gives
ΔI/I=ΔS/aS
which, after differentiating, leads to:
S=kIa
(163)
where,
unlike k in the Weber-Fechner law, which is an integer by the
starting assumption, here it can vary continuously. For a=1, thus with
the plot slope equaling 1 (45°) too, power
law coincides with Weber law, since c1=c2
and
ΔS=ΔI.
Based on his experiments, Stevens came to the following exponent values
for eye brightness response:
As mentioned, the actual values of constants in either law vary with the
choice of unit and, with the power law, k is also allowed to vary
with the adaptation level. Assuming identical apparent brightness unit,
and neglecting changes with the adaptation level (i.e. with the level of
luminous intensity), some basic characteristic of the two laws are
illustrated on FIG. 241.
As mentioned, the above is only an illustration, far from an accurate
description of eye brightness response. For instance, with intensity
plotted on the linear scale, the range of scotopic intensities
(<0.001mL, or 0.01/π cd/m2)
is an infinitesimally small fraction of the entire range of intensities
(up to 10,000mL) that the eye can adapt to. For that reason, it is
preferred to plot intensity on some kind of logarithmic scale, as it is
done on the graphs depicting more accurately eye brightness response (FIG.
242).
The above results by Stevens and Stevens are obtained using a uniformly
illuminated patch (object, target, stimulus) on a larger
background, whose luminance was determining the adaptation level. For more complex images,
specifically photographic images, Bartleson and Breneman found different
response, with the best-fit function being not a power function, but one
producing a curved, not straight, plot farther from the threshold on log-log
coordinates (FIG. 243).
FIGURE 243: Eye response to
photographic image under varying image and surround luminance (based
on Brightness perception in complex fields, Bartleson and
Breneman, 1967). Similarities vs. response with a uniform
patch are: (1) perceived brightness for any luminance level increases
with lowering the adaptation level, and (2) the rate of increase in
perceived brightness is higher for higher level of adaptation. However,
unlike the illuminated patch, where eye brightness response is well
described with a simple power function, the best fit function here has
more complex form:
According to it, perceived brightness of a complex picture is a function
of its luminance (horizontal scale) and surround (ambient) luminance.
For given picture luminance, perceived brightness, expectedly,
diminishes as the surround luminance increases (vertical plot position),
while the rate of change in the perceived brightness with the change of
image luminance (i.e. plot slope) increases with the surround luminance.
Over the extended range of surround luminance, perceived brightness
increases with picture luminance when it is of similar level (green), or
consistently higher (orange) than surround luminance. For picture
luminance consistently lower than that of the surround (blue), perceived
brightness increases with the surround luminance up to a point, after
which it nearly stagnates and, possibly, starts decreasing at high
surround luminance levels.
Unlike Stevens' graph for a uniform patch, where the visual response
(brightness) is measured against up to a several times larger background,
determining the adaptation level, brightness of a complex picture in Bertleson
and Breneman is evaluated under varying ambient (surround) luminance
levels, which is here the main determinant of eye adaptation level. The
constant 0.1 bril threshold over the range of luminance should be due to
the method of determining brightness of a complex image, by matching
brightness of image elements to that of a previously scaled series of
neutral stimuli. Effectively, the brightness scale for any given
luminance level here is comparative (relative) in its nature: this
comparative brightness is different than nominal brightness, and we use
a different word for it: lightness.
Considering similarities between the plots for simple and complex
stimulus, it didn't come as a surprise that further analyses found that
the latter can be expressed as a decline from Stevens-type power
function, that is itself a power function of the surround luminance (Choi,
1994). In
other words, Bartleson/Breneman function describing eye brightness
response to a complex image is only a more complex power-function form,
still within Steven's general postulate, which was that the human sensual response
follows power law.
But, as mentioned, unlike simple, uniform stimulus, brightness is neither
the only, nor most important attribute of a complex image. What is
usually more important is the level of contrast between its components.
This aspect of eye response can be called visual tone reproduction
of that in the original image. It is not dependant directly on the image
brightness, rather on the lightness of image elements, which
itself depends not only on the nominal brightness of image elements, but
also on the image luminance relative to that of the surround.
While both, lightness and brightness
are part of visual perception, they refer to two different perceptional
modalities. As opposed to
brightness, which is the
attribute of a visual sensation resulting from a given magnitude of
light emission (luminance),
lightness is defined as the brightness of an area judged relative to the brightness of a
similarly illuminated area that appears to be white or highly
transmitting (FIG. 244).
FIGURE 244: Neural processing produces lightness perception that
deviates from the actual intensity pattern and corresponding nominal
brightness. Change of background luminance changes perceived lightness (A,
lightness induction or simultaneous contrast; squares and
lines are all of identical intensity). So does combining areas of
different intensities (B, and C, the latter randomly
turning white circles into black).
Lightness can be thought of as relative brightness, but it is not
formally, since it does not depend on the actual intensities of picture
elements alone, rather on their visual appearance relative to each
other; elements of identical emission intensities - thus of given
constant brightness when projected against neutral background - can have
different lightnesses under different surround luminance levels. Brightness ranges from bright to dim,
while lightness ranges from light to dark.
Lightness of different areas of a complex
image is key element of its perceived contrast, which is in turn key for
tone reproduction. As such, eye response function for complex images -
i.e. visual tone reproduction - is
directly related to contrast transfer. When colors are present, hue and
saturation are also important elements of image tone reproduction. As
the plots on FIG. 243 indicate, image brightness (lightness) for
any given image luminance level increases inversely to surround
luminance. However, the increased lightness of its elements due to
darkened surrounding results in decreased
image contrast, at the rate proportional to the change in the plots'
slope. For instance, Bartleson and Breneman found that image reproduced
on a transparency (slide) and projected in dark surroundings needs to
have inherent contrast higher by 1.5 on log-log coordinates (~32 times)
than the original for the optimum tone reproduction; that corresponds to
the increase of a power function exponent (i.e. slope) by a factor of
1.5. On the other hand, printed image viewed in illuminated surroundings
only need to have identical inherent contrast to the original for the
optimum tone (contrast) reproduction.
All this only scratches the surface of the complexities of eye response
to light intensity, but should illustrate well that the common notion of
it being described as simply logarithmic is oversimplification, to say
the least. Available empirical data is based on the limited range of stimuli
form and duration, mainly brief flashes combined with some form of
background. On the other hand, telescopic
object range from point-like like stars, to complex extended images,
like planetary surfaces, and are generally a
continuous signal, less than perfectly stabilized on the retina. While
the logarithmic eye response to brightness certainly can be applicable
in some cases, it won't be in the others. In general, power low covers
more ground, which makes it more appropriate
as a general law usable for describing eye response to light intensity.
Also, distinction needs to be made with respect to eye brightness
response within any adaptation level vs. response over an extended range
of luminosities connecting a number of successive adaptation levels. The
two respective response curves are different, and the former may be, in
general, adhering closer to a logarithmic function - although not
necessarily similar between different adaptation levels - than the latter. On the other hand,
relatively short span of successive adaptation levels is nearly straight
on log log coordinates, hence should be also well fitted with a
logarithmic function.
Amateur astronomers have simple, effective means of excluding ambient
(surround) light from the equation, in which case eye response is mainly
determined by the stimulus (observed object) and its background
(telescopic field of view). But it is not unusual for the ambient
luminance to be significant factor. Hence, all scenarios are possible.
To make it more complicated, the retina is capable of selective local
adaptation, i.e. its different portions can be in different adaptation
modes.
Above considerations suggest very
clearly that there is no simple way to present the complexities of eye
response to light intensity. Less so for the telescopic eye, which
operates under conditions generally different than the typical "laboratory
eye". There is no research specific to the telescopic image of any type
that is known to me. At best, any single graph can illustrate some
basic characteristics of that response, which have only very generalized
implications with respect to how human eye responds to light intensity
when coupled up with a telescope (FIG. 245).
FIGURE 245: Eye brightness response graph for
complex image (scene) indicated by tests under laboratory conditions
(based on Gonzalez and Woods, 1992). The horizontal scale,
unlike the vertical, is logarithmic, which makes the graph greatly
compressed horizontally: going from left to right, every plot section
corresponding to a whole logarithm would be ten times longer than it is,
if plotted on linear scale. That would make both, scotopic and
photopic plots much more elongated, and especially the latter; they
would be, more or less, similar to the plots on FIG. 173 or, for that
matter, the "transitional" plots on FIG. 174/175, with the transition
from exclusively rod function (scotopic) to exclusively cone function
(photopic) much smoother than what it appears like to be here. Likewise,
the plot is "decompressed" if the vertical scale is also put in
logarithmic form, as shown in the top inset. Compressing the plot
horizontally, however, makes it easier to illustrate an important
property of eye brightness response, which is that it cannot, at any
given moment, cover the whole range of adaptations to light intensity it
is capable of. Rather, at any given adaptation level, it responds to a
significantly smaller range of luminosity, with the light signal
appearing black at the threshold level, and glaringly white at its
limit. Any prolonged exposure to light intensities closer to the
threshold, or the limit of such adaptation level, causes eye to shift to
another level. The graph indicates that such adaptation level spans
nearly four log units of the luminosity range, and only about 0.2 log unit on
the brightness scale (the latter fairly in agreement with FIG. 174/175
indicate). Within an adaptation level, brightness response is likely to
be nearly logarithmic (i.e. following nearly straight lime on log-log
coordinates) over a good portion of mesopic and photopic range. It may
deviate significantly from logarithmic toward scotopic and higher
photopic sub-range, but the specific response can vary significantly
with the stimulus type, background and surroundings.
The entire range of brightness corresponding to the range of eye
adaptation between scotopic threshold and photopic limit is, as FIG.
242/243 imply, about three logarithmic units, or 1,000 bril. At any
given adaptation level, between the absolute threshold and discomfort
level, the available brightness range is significantly narrower than
that, with a stimulus appearing black if bellow level's threshold, and
glaringly white if above its limit. As FIG. 242 suggests, this
adaptation-level brightness range is the narrowest in the scotopic mode,
with the max-to-min brightness ratio in the low single digits while the
widest in the full-blown photopic mode, when it can approach a 100-fold.
For the typical amateur, who generally observes adapted to light
conditions, it is eye brightness response within the adaptation level
that is more relevant than adaptation plot constructed over an extended
range of light intensity. If we stay away from the threshold and limit
of such an adaptation level, eye brightness response is most likely to
be nearly logarithmic - i.e. forming straight line on log-log plot - for both, simple stimulus (FIG.
242) and (nearly
so) for complex image (FIG. 243). That is probably as much as
most of the amateurs need to know. More specific information is hard to
find, since most of research was not conducted with "telescopic eye",
with the typical astronomical objects, nor under typical field
conditions. Most of the information available is only partly
relevant.
But for any accurate measurement, it is necessary to know exactly - or
as close to it as possible - what is the eye brightness response. For
instance, if human eye response to stellar brightness is not
logarithmic, but rather a power function, what would be the consequence?
The difference may not be negligible (FIG. 246).
The bottom line is that eye response to light intensity - or the
sensation called brightness - is not linear, i.e. proportional to
the light input. Rather, it is, in general, well approximated by some
form of a power function of light intensity, and in many cases it can be
also described as logarithmic. In other words, it is not the nominal
change in the light flux entering the eye that determines the change in
brightness; it is the change in the flux relative to the initial flux
magnitude.
While the exact eye brightness response is mainly important in the
professional and academic circles, the principle can be helpful to the
average amateur as well. For instance, it helps understand why the
telescopic image of the Moon appears so much brighter than looking at
the Moon directly, despite having much lower nominal surface brightness.
At 100x magnification, Moon's image area is 10,000 times larger and,
consequently, its surface brightness is, neglecting light transmission
losses, as much lower. However, to the eye, surface brightness is only 4
times lower, if the response is logarithmic, and ~20 times lower if the
response is a simple Stevens-type power function with 0.33 exponent. In
the first case, the telescopic Moon would have 2,500 times greater total
brightness (8.5 times brighter perceived integrated magnitude), and
still as many as 500 times (6.8 magnitudes) greater in the second.
Eye brightness response is related to
already mentioned eye contrast sensitivity (FIG. 240),
which defines its resolving limit as a function of luminance level and
object's (sine-wave grating) angular size (spatial frequency). MTF
analysis of the image formed by a telescope objective is not a "finished
product". To some degree, it will be changed by eyepiece aberrations
and, when finally projected onto the retina, it is a subject to the
effect of physiological processes. As a result, perceived contrast and
resolution limit will depend not only on those inherent to the image,
but also on its brightness level and angular size on the retina. The
specifics of it are described with the aid of eye Contrast
Sensitivity Function (CSF), a plot interpolated into empirical data,
as shown on FIG. 247. Note that contrast sensitivity scale us
usually shown as the inverse of unit (100%) contrast, i.e. 1% sensitivity
required is 100, 0.5% is 200, and so on. Plot is for the central retina
(fovea); contrast requirement generally increases toward periphery.
Also, it is important to remember that the eye CSF is a sum of the
optical input and its neuroretinal processing. In general, processing
enhances the CSF of the optical input alone.
FIGURE
247: Minimum contrast needed by the eye to resolve MTF-like
(sine-wave) pattern, varies with its illumination level and
angular size on the retina. Both, spatial frequency (in cycles/degree)
and contrast level are given in logarithmic form, to "magnify" the
effect at the level of a fraction of the percent in the contrast scale,
as well as the effect in the range of large details. Detail size on
the retina is given in cycles/degree; 60 cycles
per degree is the conventional limit to eye resolution of 1 arc
minute. Contrast sensitivity, as a function of detail size and
retinal illuminance, is defined by the minimum contrast level at which
the image remains resolved. For instance, 10 cycles/degree (6 arc
minutes) image size requires 0.6-0.7% minimum contrast in photopic (bright-light) conditions,1-2% in average mesopic conditions, and
10-15% in
average scotopic (low light) conditions. Contrast sensitivity peaks
for ~9' detail size in photopic conditions,
shifting toward larger details in mesopic and
scotopic conditions. At the same time, maximum contrast sensitivity
diminishes from nearly 0.6% (photopic) to nearly 2% (scotopic).
Limiting resolution, at 100% contrast level (along the horizontal
scale), also diminishes noticeably with the decrease in illumination
being, as expected, the highest in bright-light conditions, and
lowest in low-light conditions. The significance of the CSF for
astronomical observing is in helping to determine optimum
magnification level for details and objects of different luminosity
levels. Like other eye properties, contrast sensitivity can vary widely
individually. It is not determined by the quality of the eyesight; an
individual with poor eyesight can have better than average contrast
sensitivity, and the other way around.
Contrast sensitivity is also
age related, but not as it might be expected. Graph at left shows
that in the 40's - and, in part, even 50's - it is better than in the 30's (some studies found it
is better than in the 20's too, at least for some frequency ranges).
In young age it is worse vs. older age, and keeps getting better
toward the old age (it may have more to do
with the quality of neural processing than optical quality). This
particular study was limited to 18 cycles per degree (3.3 arc minute
line width), but the trend toward highest frequencies is obvious,
with the CFS expectedely taking a dive approaching cutoff
frequencies at 100% (i.e. 1) contrast level.
Aberrations
in general have negative effect on contrast sensitivity, but in
some cases they can make it better. Unfortunately, aberrations'
contrast transfer function can't be directly applied to the CSF
as degradation factor because of the role of neural processing, which in general
enhances optical input, but in various ways i.e. specific to the
patterns, shapes and intensity levels.
◄
13.7. Combined eye aberrations,
diffraction
▐
13.9. Eye spectral
response
►
|
||||||||||||