|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
1. Rays and waves
▐
1.1.(cont'd) Point spread function ► 1.1. DIFFRACTION
PAGE HIGHLIGHTS As a consequence of the existence of diffracted wave energy, placing obstruction of some form in the light path will result in the "emergence" of this energy in the space behind obstruction. But the obstruction did not change anything in the way the light propagates - it merely took out energy of the blocked out principal waves, with the remaining diffracted field creating some form of intensity distribution in the space behind obstruction - the diffraction pattern. Likewise, the geometrically unobstructed field in the proximity of obstruction will change due to the absence of contribution from the blocked out portion of the field. It is this second aspect that is relevant for image formation in a telescope.
By limiting energy field to an aperture, the portion passing through it is separated from the rest of the field, and its energy - this time consisting from both, aperture-shaped principal waves and diffracted waves from within - will create a pattern of energy distribution behind the aperture. Again, there is no actual change in propagation for the light passing the aperture, including those close to the edge of obstruction (light does not "bend around the edge"); whatever the form of energy distribution behind the aperture, it is caused by the interference of the primary and diffracted waves inherent to the energy field (FIG. 1, middle and bottom). It is due to the missing portion of the field - the one left out of the aperture - that the field after passing it changes, with the diffracted field having different spatial amplitude distribution than the incident field. It turns out, complex amplitude diffracted to infinity is proportional to the Fourier transform of the field (i.e. its complex amplitude) in the aperture. For the circular aperture with even transmission, this transform takes the form of the Amplitude Transfer Function, the square of which is the Point Spread Function (PSF) for circular aperture. The intensity pattern created at infinity by the diffracted field can be brought to a finite distance by an optical objective that converges diffracted field to the image plane.
Fraunhofer and
Fresnel diffraction
In calculating diffraction effect, the basis is the path length of
diffracted waves, which determines their phase at a point of
interference, thus also the complex amplitude and the wave energy at
this point. Fraunhofer and Fresnel diffraction are terms referring
to the approximations used for calculating path length of the
diffracted wave. They can be based on either (complete) Rayleigh-Sommerfeld,
or (less complete) Fresnel-Kirchhoff diffraction integral. The basic
concept is that of plane wave propagation in free space, illustrated
on FIG.1 (middle). Since the path length (PL) of a diffracted wave
is the hypotenuses of a right-angle triangle whose two sides are the
height of the point of origin relative to the point in the plane of
interference (h) and the distance between the planes of
origin and interference (s), it is given by (h2+s2)1/2.
This can be expanded into a series PL=s+r2/2s-r4/8s3+...,
with the second term being referred to as defocus term and
the third as (primary) spherical aberration term (these are reffered to as "aberrations of the diffracted wave"; they are
not the conic surface aberrations, and the terminology is based on the
superficial form identities).
Diffraction image In order to form the image of a point-source, portion of the energy field emitted by it needs to be brought together, creating a patch of highest energy concentration - a point-source image. For this, the primary waves need to meet in a single point in the same state of propagation - or phase - which, in turn, requires that optical paths from all wavefront points are identical. The more difference in optical paths, the less efficient wave interference, resulting in deterioration and, ultimately, disintegration of the point-image. Obviously, this ideal wavefront shape for the purpose of optical imaging is a sphere, with every point on it at identical separation from the center of curvature. Waves from spherical wavefront arriving at its center of curvature - or focus - all meet in phase, for the maximally efficient energy concentration into a point-image. However, this point-image is not a point of light, but an extended pattern of intensity distribution (Inset A). The reason are residual wave interactions around the point of convergence, the concept introduced by Fresnel. This effect is known as diffraction of light, i.e. interference effect of the diffracted waves. As a result, light energy directed toward focal point is spread into a cone of converging energy focusing into a 3-D pattern of energy distribution that sets the limit to image contrast and resolution.
Similarly to the single pair of emitters, this complex superposition of waves onto the image of a point-source forms a series of subsequent minimas and maximas, which in a circular aperture appears as a pattern of concentric bright rings of rapidly descending intensity. Since the spatial limitation of the aperture effectively creates obstruction to propagation of waves outside of it, the waves entering the aperture become diffracted waves, and their interference pattern becomes diffraction pattern. In another analogy to a single pair of emitters, where the angular separation between subsequent minimas and maximas is in inverse proportion to their separation, angular size of the pattern in aberration-free circular aperture is inversely proportional to the aperture diameter. Unlike the simple two-wave interference, as mentioned, complex superposition of waves in a telescope results in the constructive interference rapidly diminishing with the increase in pattern's angular radius, the consequence of most points in the pupil being at relatively wide separations. Physical size of the diffraction pattern in the plane of best focus is inversely proportional to the telescope's relative aperture 1/F, with the first minima (Airy disc) radius given by rAD=1.22λF, λ being the wavelength of light, and F the focal ratio F=f/D, f and D being the telescope focal length and diameter, respectively. However, the effect on image quality is not directly related to the physical size of the pattern, rather to its angular size, as subtended on the sky, and the object itself, through the pupil (aperture) center. Its radius is given by αAD=1.22λ/D, in radians. Angular size of diffraction pattern (i.e. of the point-source image) in a telescope sets direct limit to its theoretical resolution and maximum useful magnification. Follows more detailed description of how diffraction shapes the point-source image formed by a telescope.Diffraction in a telescopeOptically, any astronomical object is composed of a countless number of point-sources of light. The telescope forms object's image by imaging each and every of these point sources in its focal plane. The point-image itself is created by wave interference around focal point, due to the phenomenon known as diffraction of light. It is often thought of as being caused by an obstruction placed in the light path. In fact, diffracted energy is inherent to the propagation of energy fields, and the presence of obstructions in their path merely changes the field properties by excluding a portion of it. This produces various interference - or diffraction - effects in the image space. In the case of a telescope, the obstruction in the light path is effectively in the plane surrounding the aperture. Most reflecting systems also generate an additional diffraction effect from the obstruction by a smaller, secondary mirror. Diffraction image of a point-source in a telescope is a bright central disc surrounded by rapidly fainting concentric rings. As already stated, this pattern is created by the interference of light waves. Constructive interference is at its peak in the center of the pattern, which is the center of curvature of near-spherical wavefront formed by telescope's objective. Farther away from the center point, constructive interference quickly subsides, resulting in the first bright ring much fainter than the disc, and every successive bright ring much fainter than the preceding ring. Size of diffraction pattern in a telescope is proportional to the wavelength λ; given wavelength, its physical size is proportional to telescope's F-number (focal ratio, F= f/D), while its angular size is inversely proportional to the aperture size (FIG. 2).
The basics of diffraction can be illustrated with interference of light emitted by an arbitrary pair of points on the wavefront formed by a telescope objective. Energy unit of an actual wave is photon - quanta of energy defined by the product of wave frequency (number of wave cycles per unit of time) and Plank's constant, h=6.6256x10-34 in joules (J). In the following text, wave interference and resulting energy are described in terms of normalized unit amplitude A - with wave amplitude defined as the maximum value of its oscillation - and resulting intensity I=A2 (electromagnetic wave oscillates in two perpendicular planes, with the field energy proportional to a product of their equal amplitudes) of the light wave. Optical path difference (OPD) for any pair of emitters on the wavefront in the pupil of a telescope is closely approximated by: OPD = Ssinα (a) with S being their linear separation in the pupil, and α the angular radius of a point in the image space (Inset A). The angle α at which wave interference becomes destructive is directly related to the linear point separation (S, Inset A), which defines optical path difference, as given above, and the resulting phase difference in radians as ΔΦ = 2πOPD/λ = 2πSsinα/λ (a') The angular image radius α at which any given phase difference will be generated is, therefore, dependant on the point separation S. Taking, for instance, phase difference ∆Φ=π (which, with the full phase spanning the wavelength, or 2π=λ, corresponds to λ/2 OPD), for a pair of wavefront point-emitters separated by S=λ/2 in telescope pupil, gives the corresponding angular image radius (i.e. radius of the first minima), rather obvious, as α=90° (from sinα=OPD/S=∆Φλ/2πS=1). Given OPD, the efficacy of wave interference depends on their degree of coherence. Two waves are coherent if their phase differential is constant. Strictly talking, light is coherent if monochromatic, originating from a point, and has a constant rate of emission; this ensures that the energy field has perfectly uniform time-independent propagation pattern. Such wave is spatially and temporally coherent. As the spatial extension of light source increases, at some point the separation between individual emitters becomes large enough to cause a significant phase differential between their fields at some distant point, resulting in some degree of spatial incoherence. Also, different points radiate independently and the waves they emits become less coherent, with their coherence time, or temporal coherence - defined as the time interval t within which the field has nearly identical phase continuum - diminishing. So instead of having long trains of nearly uniformed field oscillation pattern, light consists of many smaller wave trains with varying phase properties. Spatial period corresponding to the coherence time, spatial coherence or coherence length l is l = ct, c being the speed of light. Also, as the frequency range of light Δν in Hertz increases, its temporal coherence diminishes as t~1/Δν. For white light, with the frequency range of about 320 trillion Hz (with frequency given as ν=c/λ), temporal coherence - assuming near uniform intensity over the range - is about 3.1x10-15 seconds, with the corresponding coherence length l~0.00094mm. This incredibly fast pace of variation in the configuration of wave trains contained within the continuum of temporal/spatial coherence intervals results in suppression of the fringe pattern, as a consequence of wave interference in low-coherence light (Inset H, would have been between the top two patterns, with Δλ~0.55λm). In a different context, polychromatic light with all the wavelengths emitted simultaneously and continuously from a point-source is temporally coherent in vacuum only within narrow wavelength range, because specific phase at any given point in time varies with the wavelengths. But it is spatially coherent, because all waves come from the same point. The degree of light coherence for near-monochromatic light is expressed by its complex degree of coherence value ɤ, ranging from 1 (coherence limit, or complete coherence) to zero (incoherence limit, or complete incoherence), with the intermediate values that significantly differ from 1 or 0 indicating partial coherence.
Following page expands on the properties of the building block of any
telescope image, the diffraction image of a point source of light, described by Point Spread Function, or
PSF. ◄ 1. Rays and waves ▐ 1.1.(cont'd) Point spread function ►
|
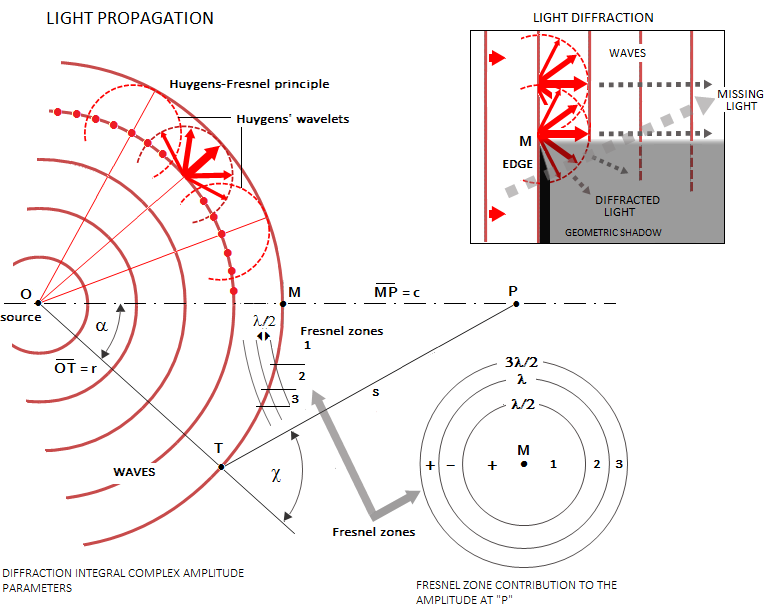
The simplest approximation of the complete diffraction integral -
the Fraunhofer integral - accounts only the first term, hence
applies only for very small angles (cos→1)
- i.e. large distances - for which the difference between PL and
s is negligible. Fresnel
integral also accounts for the second, defocus term. Thus, the
difference between Fresnel and Fraunhofer approximations is in the
distance between diffracting aperture and plane of observation to
which one can be applied; the former can be applied to much smaller
distances (near-field diffraction) than the latter (far-field
diffraction). For very small distances, Fresnel integral also
becomes inaccurate, and a complete integral like Rayleigh-Sommerfeld
is required. Such integral is also applicable to larger distances (Fresnel
and Fraunhofer regions), and Fresnel integral is applicable to the
Fraunhofer region, but more accurate integrals are more complex, and
only used when necessary. 
