6.6.  MTF - Modulation transfer function

FIGURE 100: The magnitude and phase aspect of the OTF. The former expresses the effect on intensity modulation i.e. contrast (top), the latter on the spatial distribution (bottom). OTF magnitude depends solely on the relative magnitude of the minimum intensity of the sinusoidal pattern (IMIN) vs. its maximum (IMAX). In order to incorporate the effect of a possible phase shift, OTF is constructed within a unit circle in complex coordinates, with its real and imaginary parts reflecting the magnitude of phase shift, but not the OTF magnitude itself, which is in these coordinates given by a square root of the sum of squared real and imaginary parts of OTF, therefore remaining unit value independent of the phase shift (bottom right).

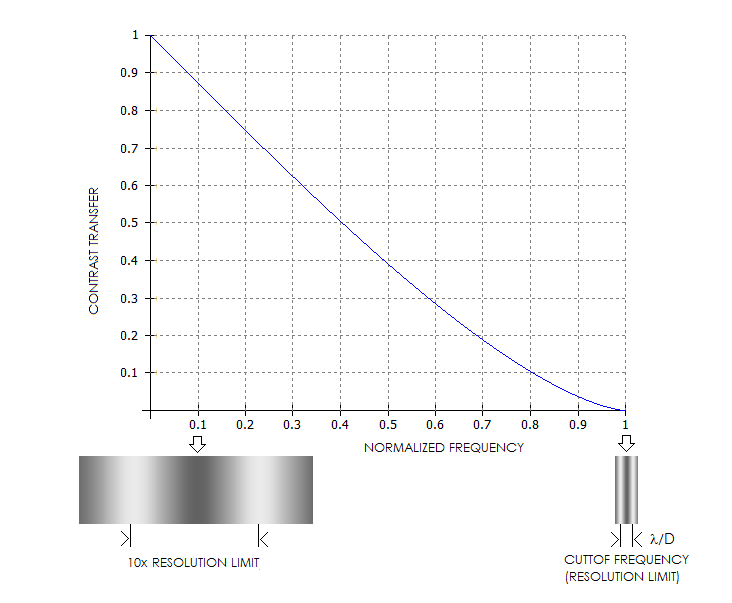
INSET A: TOP LEFT: Standardized MTF object form is a continuum of parallel, equally spaced bright contrasty lines on dark background, with irradiance modulation defined as infinite sinusoidal distribution. The line width, equaling that of the dark/light pair, is inversely proportional to the spatial frequency ν, normalized to 1 at the cutoff frequency D/λ cycles per radian (the inverse of the angular limit to resolution λ/D in radians, D being the aperture diameter), where image contrast drops to zero (linear cutoff frequency is the inverse of the linear limit to resolution λF, or 1/λF in lines per mm, for λ in mm). This form of intensity distribution can be represented as periodic sinusoidal wave, with the contrast determined by the relative intensity of its maxima vs. minima. Image of this pattern has the relative intensity and contrast dampened due to the effect of diffraction, whether without or with aberrations present, At any given frequency, MTF is a ratio of the output (image) to input (object) modulation amplitude. Mathematically, it is Fourier transform of the system's PSF (more specifically, it is an integrated sum of the PSFs for every point over its intensity distribution profile, i.e. convolution of object's Gaussian image and aperture's PSF). At the limit of resolution for aberration-free aperture, the line width is nearly equal to the aperture's FWHM.



 TOP RIGHT: The modulation transfer function - MTF - for clear aberration-free aperture (P) is the ultimate limit to the overall contrast and resolution set by diffraction for this type of object. Normalized to 1, it equals the relative overlapping area of two circles of unit diameter (graphic representation of pupil autocorrelation), at a center separation ν, the normalized spatial frequency (top right, yellow overlap area for ν~0.3). MTF in aberrated aperture (A, 1/4 wave P-V of spherical aberration) is lower than P over the entire range of frequencies.
The standard MTF plot is non-linear, in that any given linear change of contrast is proportional to the normalized frequency (i.e. same linear change at, say, 0.5 frequency is about twice the relative change at 0.25 frequency).
The relative contrast (RC) shows contrast differential between the two more clearly, directly comparable, in units of the perfect aperture contrast level normalized to 1 over the frequency range.
The low-contrast thresholds for bright (LCB) and dim (LCD) details, is an informal, but useful addition by Rutten and Venrooij. It indicates that the approximate cutoff levels for typical low-contrast details - about 10% inherent contrast - requires higher minimum contrast at the resolution limit than the standard bright, contrasty MTF pattern. As a consequence, their cutoff frequencies are lower than for high-contrast details. The original plots are constructed with respect to a perfect aperture transfer line starting at 0.1 contrast for zero frequency, decreasing toward zero at the regular cutoff frequency, with the limit to resolution determined by the minimum contrast required by the eye, approximated at 5% for the bright and 2-3 times as much for dim details, both steadily increasing from low toward high frequencies; the LCB and LCD lines above are based on these plots, only with the contrast at zero frequency normalized to 1, i.e stretched out tenfold vertically. The two lower threshold lines are for bright and dim details with 100% inherent contrast. As shown, the approximate resolution limit is 1/2 and 1/7 of the standard MTF cutoff frequency for bright and dim
low-contrast objects, respectively. For contrasty dim details (HCD, High-Contrast-Dim), the approximate minimum contrast level HCD indicates the limiting resolution of about 0.7 frequency. It is somewhat better for contrasty bright detail (HCB) - near 0.9 frequency - but the resolution limit would require the maximum contrast. Again, these are only general approximations, and may be inaccurate, particularly toward cutoff frequency, since the actual minimum contrast required by eye increases exponentially close to the limit of resolution (FIG. 236C).
Note that different patterns of intensity distribution have different contrast transfer; for instance, periodic square wave (i.e. pattern of sharply defined dark and bright lines) will have contrast transfer higher at all frequencies either in aberration-free aperture (solid blue line), or for any given level of aberration, as the CTF for clear aberration-free aperture (blue plot) indicates. However, the relative change in contrast transfer due to aberrations and/or obstructions are generally similar for MTF and CTF.

INSET B: As mentioned, the complete OTF describes both, contrast transfer, or modultion (MTF), and phase transfer from object to its image. Phase transfer can only occur if diffraction peak is displaced away from the intersection of chief ray (one that passes through the center of the aperture stop) and image plane. That causes lateral shift of the MTF bar pattern, as illustrated below for coma (left) and defocus (right). Of all conic aberration forms, only coma induces phase shift due to its asymmetric PSF, except when its axis of aberration ( i.e. axis of symmetry for the geometric blur) is parallel with MTF bars. Other conic aberrations can also induce phase shift, but as a consequence of the change in PSF intensity distribution. Shown are only coma PSFs for a few selected points on the object (MTF pattern subjected to imaging) are shown, but the actual calculation includes PSFs from all points of the object-pattern. The combined amplitude they produce at every point in the image plane determines the intensity pattern of the image-pattern, i.e. its contrast transfer characteristics (note that PSFs shown are independent, not a convolution of the Gaussian image, thus the image pattern is only an illustration).
The PSF peak shift for λ/2 wave P-V of primary coma (0.088 wave RMS) is λF, which is on this illustration about 1/7.5 of the full phase of the sinusoidal pattern (indicating the corresponding pattern frequency as 7.5 times the λF cutoff frequency, or ~0.13 , resulting in 2π/7.5 phase shift of the MTF pattern. Phase shift does not affect contrast transfer, which is determined by the combined wave amplitude itself, which is MTF domain. Since the PSF shift, when present, has constant value, the corresponding phase shift varies across the range of frequencies, and can be plotted as a separate PTF.

At right, shown is the effect of 1 wave P-V of defocus on the image of an object that is not the standard MTF pattern, but one in which bar width is oriented horizontally, with the line width changing continuously according to the spatial frequency. Top image (A) is aberration-free, and bottom (B) defocused one. If the aberration is large enough - in the case of defocus ~0.9 wave P-V or larger - image of such object will show contrast reversal - where bright lines become dark and vice versa -  indicated by the OTF, but not the MTF. The reason was immediately apparent from the PSF intensity distribution for 1 wave of defocus, developing dark circle (minima) at the center of the pattern. Hence, MTF does provide information on contrast transfer, but not on the image itself. To reconstruct the image, we need OTF. This, however. may have significance only with large aberrations, generally about 1 wave P-V and larger (a few more examples at ). OTF for smaller aberrations does not fall below zero, thus there is no contrast reversal to affect image.
As plot at right show, the standard MTF output by OSLO (dashed) does not equal the absolute value of OTF, indicating that MTF plot may vary somewhat depending on the algorithm applied. If defined as the absolute value of OTF magnitude, MTF should continue through the red plot section.

INSET C: In addition to phase shift, if PSF intensity is varying radially it will also cause different contrast transfer for different orientations of the PSF relative to MTF pattern. A complete MTF integral has radial component, thus it integrates for all orientations of the PSF relative to the line pattern. Graphically, it is represented by a volume figure, formed by continuous change of the integration angle (i.e. pattern orientation) through a full circle, or 2π radians (right). This volume may be looked at as a total contrast, transfer.
For radially symmetrical aberrations, like spherical or defocus, there is no variation in contrast transfer with orientation, and it is fully represented by any single orientation, i.e. 2-D MTF. For radially asymmetrical aberrations, like coma or astigmatism, the transfer, hence also the MTF volume cross section profile, changes with the orientation, forming rotationally asymmetrical 3-D figure. The default representation is often to show MTF for sagittal  (perpendicular to MTF bar orientation) and tangential (along bar orientation) PSF orientation. This works well with coma, where it assesses the two limiting effects, the minimum (the latter) and maximum (former), giving a good idea of the average effect on contrast transfer. With astigmatism, however, which at the minimum variance focus causes a cross-like PSF deformation, with 0 (π) and π/2 (3π/2) PSF rotation producing the same effect, while the maximum effect on  MTF contrast transfer is for π/4 (+π) PSF rotations.
Contrast transfer for all PSF orientations also can be azimuthally averaged, giving mean contrast transfer for the aberration.

INSET D: Note that the graph on top represents monochromatic MTF (as indicated by the cutoff frequency 1/λF). Polychromatic MTF cutoff frequency - and to a slight extent, the overall shape - is determined by the combined PSF intensity distribution within the wavelength range. As large inset at right illustrates, while PSF for individual wavelengths differ significantly at the ends of given spectral range (first minima being at 1.22λF), when combined they nearly offset around the central wavelength's PSF. Actual PSFs

 for different wavelengths also normally differ in their intensity, both emitted by object and perceived by eye, which may affect contrast transfer by giving to it bias toward the wavelength of maximum intensity, since the intensity distribution loses the symmetry around central wavelength). There is little difference between centered monochromatic (green) and full-range polychromatic PSF (black), thus also MTF, regardless of the sensitivity mode. The PSF differ mainly in the ring area (photopic vs. even spectrum, small inset), and with MTF it is limited to the value of cutoff frequency, which is for polychromatic light determined by that for the shortest wavelength. This is based on the formalism describing polychromatic contrast transfer as the average sum of the transfer c for given frequency ν at each of i wavelengths, MTF(ν)=Σc(ν)i/i. As a result, long and short wavelengths nearly offset each other for the most of frequency range, with the resulting polychromatic MTF for the range gravitating toward that of the mid-wavelength; some residual contrast transfer extends beyond that for the central wavelength, not significantly influenced by eye sensitivity factor. While the nominal cutoff frequency for polychromatic MTF equals that of the shortest wavelength, it actual contrast transfer is much closer to that of the central wavelength.

FIGURE 101: PSF and MTF plots for clear aberration-free aperture (black), and aberrated (red) at the 0.80 Strehl level, and that wavefront error doubled.

DEFOCUS: 1/4 and 1/2 wave P-V. Doubling the error halves the peak PSF intensity (Strehl), but the average contrast loss is three times greater (20% vs. 60%, given as a ratio number by the differential between the Strehl and 1). Note that the Strehl for 1/4 wave WFE of defocus is slightly higher than 0.80.
 

PRIMARY SPHERICAL ABERRATION: 1/4 wave and 1/2 wave P-V errors have nearly identical effect on the PSF maximum as with defocus, but the more widely spread energy causes more of contrast loss at the lower frequencies, while the smaller central maxima results in somewhat better transfer at mid-to-high frequencies. The transfer is again inferior near the cutoff due to the smaller bright core with defocus. Being close to zero, the cutoff frequency for 1/2 wave P-V is about 20% lower in field conditions.

PRIMARY COMA: 0.42 and 0.84 wave P-V have similar effect on the PSF peak value as 1/4 and 1/2 wave P-V of defocus or primary spherical. However, the actual contrast transfer varies significantly with the orientation of the asymmetrical aberrated pattern relative to MTF bars. It is the worst when the blur length is perpendicular to the bars (red), and the best when blur length has the same orientation (green). MTF plots hitting zero contrast near the cutoff and bouncing after, indicate contrast reversal.

PRIMARY ASTIGMATISM: The effect of 0.37 and 0.74 wave P-V is similar to 1/4 and 1/2 wave of defocus in that the energy spread out of the Airy disc is mostly contained closer to central maxima, resulting in less of contrast loss at low frequencies. Unlike defocus, does not change radial symmetry of PSF, astigmatism gives to it cross-like shape which, similarly to coma's asymmetry, gives the best contrast transfer when cross orientation is identical to that of the bars (green) and the worst when it is at 45° angle.

TURNED EDGE: 2.5 waves P-V is needed that turned edge starting at 95% the radius to lower the Strehl to 0.80. Lost energy is evenly spread wide out (the abrupt initial contrast loss ending at about 1/40 frequency indicates the radius of this spread as 40 times the cutoff frequency, or 40λF - over 30 times the Airy disc radius). Odd but expected TE property - due to the relatively small affected area (the RMS for 0.80 Strehl is whooping 0.28 wave) - is that increasing the aberration does almost no additional damage.

ROUGHNESS: ~1/14 and ~1/7 wave RMS of roughness producing asymmetric PSF pattern, thus having contrast transfer vary with its orientation relative to MTF bars. Due to the random nature of the aberration, the P-V wavefront error can vary significantly for any given RMS/Strehl level. IHere, the P-V error ranges from -0.169 (blue speck on the wavefront map) to 0.374, and -345 to 0.745, respectively. RMS error also may not be as reliably related to the Strehl as with most other aberrations.

PINCHING: 0.37 and 0.74 wave P-V of wavefront deformation caused by edge pinching at a three 120° separated points has the typical
3-sided symmetry (trefoil). the aberration is radially asymmetric, causing the contrast transfer to vary between the maximum (red, for zero, 120° and 240° orientation angle) and minimum (60°, 180° and 300° orientation). Other forms do occur, with or without some form of symmetry. About 30% of the frequency range toward high end shows contrast reversal.

TUBE CURRENTS: 3/4 and 1.5 wave P-V wavefront error caused by tube currents affecting end 30% of the wavefront radius. Energy spreads mainly in the direction of wavefront deformation. Similarly to the TE, the RMS error (0.106 and 0.212, respectively) is disproportionally large vs. Strehl, and doubling the error has relatively small effect. Contrast transfer is the worst when the energy spreads orthogonally to MTF bars; for the aberrated energy spread having the same orientation as MTF bars is perfect (green).

SEEING ERROR: Averaged PSF/MTF effect of ~1/14 and ~1/7 wave RMS of atmospheric turbulence. The P-V error can vary substantially (here is 0.43 and 0.86 wave, respectively). Seeing error fluctuates constantly around the average, as do the corresponding image contrast and resolution. Larger seeing errors (1/7 wave RMS is rather common with medium size apertures) reduces contrast level to that similar to twice smaller aperture for low-to-mid frequencies, with some high-frequency transfer (iincluding limiting resolution) advantage remaining.

MTF contrast transfer generalized to the RMS wavefront error alone, regardless of the type of aberration is, as shown by Bob Shannon, given by a product of aberration-free MTF and the Aberration Transfer Function [ATF=1-(ω/0.18)2(1-4(ν-0.5)2), where ω is the RMS wavefront error in units of wavelength, and v is the normalized spatial frequency; not to confuse with the Amplitude Transfer Function - this is the only place where the Aberration Transfer Function is mentioned] for any given level of the RMS error, and aberration-free MTF, as illustrated at left for selected levels of RMS wavefront error (ω). It clearly shows that contrast transfer does not drop linearly, but exponentially with the increase in the RMS error. While the contrast loss is still negligible for ω=0.037 (1/8 wave P-V of primary spherical level), it is several times larger at the error doubled. Another 50% higher error, to 0.10 wave RMS, nearly doubles the loss, but yet another 50% increase, to 0.149, more than doubles the entire contrast loss at ω=0.10.
Also, with the increase in error magnitude, maximum contrast drop gradually shifts from the lower mid frequencies to the mid frequencies.
With small-to-moderate RMS wavefront errors, this generalized MTF can be assumed to also represent the averaged contrast drop for a given RMS error for asymmetrical aberrations, like coma and astigmatism, or for irregular wavefront deformations characteristic of the actual systems (due to their asymmetric form, such aberrations have contrast transfer varying with the MTF orientation). However, since the differences in contrast transfer over MTF frequency sub ranges for different aberration forms generally increase with the wavefront error - especially as it exceeds 0.15 wave RMS - the usefulness of this generalized MTF approach diminishes going beyond that level.