◄ 10.2.2.4. Schmidt-Cassegrain telescope   ▐    10.2.2.4.2. SCT focusing errors ►
 

10.2.2.4.1. Schmidt-Cassegrain off-axis aberrations

Since Schmidt corrector doesn't induce appreciable abaxial aberrations, in Schmidt-Cassegrain telescopes they are induced by the two mirrors alone. Off-axis aberrations in an SCT - particularly coma and field curvature - can be significant. Although both can be corrected with certain design parameters satisfied, this is not the case with most commercial types, which opt for acceptable optical quality, minimized production cost and broadest commercial appeal. For instance, coma correction would require either aspherizing one of the mirrors, or compromising the ultra-compact design. The former has been tested in commercial units in the recent years (Meade) with not much of a success, mainly due to the overall production quality still being mediocre.

In general, SCT astigmatism is low, but coma is typically strong. Follow relations for determining specific values of these aberrations.

● lower-order coma P-V wavefront error for object at infinity is given by:

with the system coma aberration coefficient cs being the sum of the individual aberration coefficients for the two mirrors, cs=c1+c2, and α the field angle. Not surprisingly, there is a direct similarity with all-reflecting two-mirror systems, the only difference being in the position of aperture stop. The individual coma coefficients for SCT primary and secondary, respectively - with the secondary's coefficient adjusted for the difference in ray height, so that the two can be directly added - are given by:

with σ1 being the primary mirror stop separation in units of the primary radius of curvature (with the stop at the corrector, σ1=-sc/R1, sc being the corrector-to-primary separation, positive in sign), m the secondary magnification, and

is the secondary mirror stop separation (i.e. exit pupil, or image of the aperture stop formed by the primary to secondary separation), in units of the secondary's radius of curvature (pupil-to-secondary separation is numerically negative for the aperture stop located inside primary's focus); as before, ρ=R2/R1. In the typical f/2/10 commercial SCT (i.e. with secondary magnification m~5), k~0.25, σ1~0.4, ρ~0.31 and σ2~-7.6. Note that the negative value of σ₂ gives negative value to the secondary's coma coeficient, which means it is of opposite sign to that of the primary. Using these approximate values gives c₁=0.6/R₁², and c₂=-0.4125/R₁², with the system coma aberration coefficient c_s=0.1875/R₁. For R₁=-800mm, i.e. an 8-inch SCT, the corresponding P-V error is W=0.195α, with α being the field angle in radians (for small angles equaling the angle tangens). Putting W=0.00023mm, for the value equaling 0.42 wave P-V (550nm wavelength), or 0.80 Strehl, gives α=0.00118, i.e. the corresponding field angle 0.068° and field height 2.37mm. With "diffraction-limited" field radius, with repect to coma, h=F³/90 in mm, this implies that an 8-inch standard SCT has coma-limited linear field comparable to an f/6 paraboloid (from F³=90h).

     Taking σ1~0.4 (it does not change significantly with the change in secondary size within practical range), and substituting for k and ρ in terms of secondary magnification m, gives a good approximation in terms of secondary magnification as σ2~(η-5m-4)(m-1)/2m(1+η), where η is the back focal length in units of primary's focal length. For the standard η=0.5, the secondary mirror stop separation is σ2=0.5-(5m/3)+(3.5/3m).

Setting c1=-c2 gives the secondary conic needed for zero coma as:

This conic only corrects the lower-order coma. The higher-order coma in the SCT is low, about 5% of the lower-order coma magnitude, and of the same sign. This means that correcting for this residual higher-order coma - actually, minimizing it by balancing with the lower order coma of opposite sign - requires about 5% stronger conic, which will induce lower order coma needed to minimize the higher-order term.

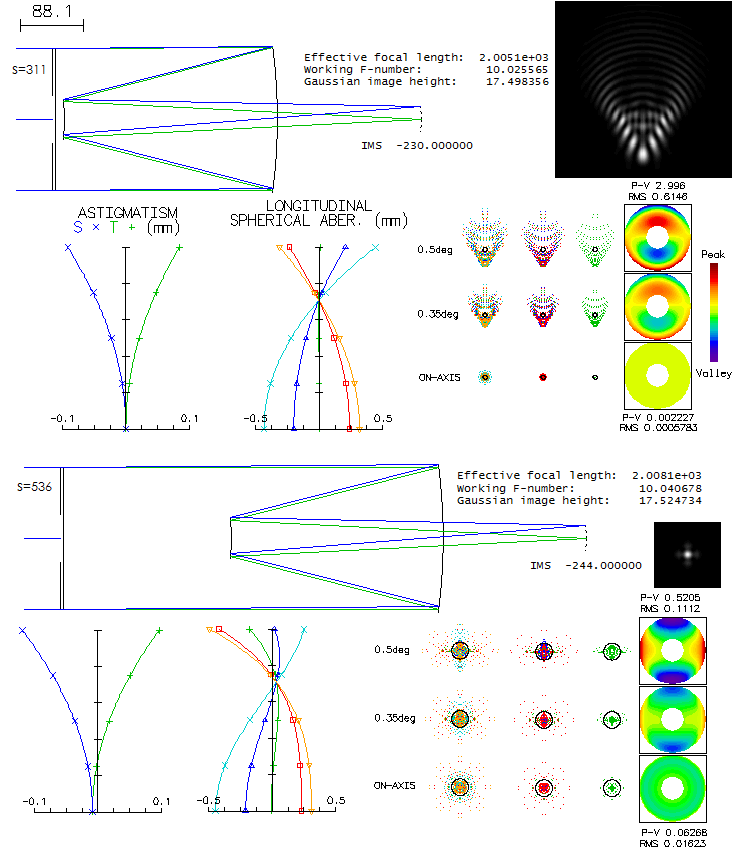
Graph at left shows the secondary conic needed to correct coma as a function of secondary magnification, based on Eq. 116.2), for the back focal length η=0.5. Since the change in magnification also changes the secondary size, as k=(1+η)/(m+1), radius of curvature, as ρ=mk/(m-1) and secondary stop separation σ2, these are substituted in the equation to obtain accurate conic value (corrector location is assumed constant, with σ1=0.4, since the change in its value are near negligible). The coma correcting secondary is an prolate ellipsoid for secondary magnifications of about 4.5 and larger, paraboloid for magnification just over 4, and a hyperboloid for lower magnifications. The required nominal conic increases sharply for secondary magnifications lower than 3, as the secondary increases in size, and its surface becomes less strongly curved.

Alternative expression for needed secondary conic for zero coma using aggregate parameters can be written as K2=[(BA+1)A-(2-2σ1)C)]/(1-B), where A=(m+1)/(m-1), B=(1-2σ1)k and C=[m/(m-1)]3. Similarly, needed conic for the primary in the standard f/2/10 arrangement with spherical secondary would be little below 0.5 (oblate ellipsoid) for correcting lower-order coma alone, and little above 0.5 to offset the higher-order component as well. It would require significantly stronger corrector, resulting in about 75% larger spherochromatism.

Needed σ1 value for zero coma in the arrangement with two spherical mirrors is σ1=[2C-(kA+1)A]/2(C-kA2). Alternately, it can be expressed in terms of ρ and k as σ1=[2ρ3-k2(2ρ-k)(2ρ+1-k)]/2[ρ3-k2(2ρ-k)2].

The standard commercial SCT has both mirrors spherical, thus K1=K2=0. Obviously, coma in such arrangement is not corrected; for the linear field, the standard 8-inch f/2/10 SCT is approximately at the level of an f/6.1 paraboloid, with the coma increasing to the diffraction-limited level (0.80 Strehl) at about 2.5mm off-axis. Larger SCT apertures have somewhat more coma, since they use a smaller secondary (due to the relatively smaller back focal length); for instance, in an 11-inch standard SCT coma is about 15% larger.

SCT system satisfying Eq. 115.2 is so called aplanatic SCT (Fig. 175b). It recently became commercially available advertised as the "improved Ritchey-Chretien". While admittedly with less astigmatism than comparable RC, it is - needless to say - still "only" an aplanatic SCT.

Another option for correcting the coma is to keep the mirrors spherical, but move the corrector (i.e. stop) farther away from the primary. Taking the common ~f/2/10 system with k~0.25, ρ~0.31 and m~5 gives secondary stop separation σ2~0.4-[1.6/(1-2σ1)]. Substituting these values in the relation for secondary's aberration coefficient (Eq. 116) gives c2=0.288σ1-0.528 (omitting common denominator R1) which, after setting c2=-c1 thus 0.288σ1-0.528=-(1-σ1), gives needed corrector separation for corrected coma as σ1=0.663, or nearly 2/3 of the primary mirror radius of curvature. Moving corrector that far from primary induces negligible changes in the correction level of other aberrations, thus can be applied to a system optimized for the compact arrangement. As shown below, on a 200mm f/2/10 system, it induces less than 1/10 wave P-V of spherical aberration (undercorrection), and slightly increases astigmatism, resulting in a slightly weaker best field curvature.

Chromatic correction is unaffected, with the only remaining off axis aberration being low magnitude astigmatism (diffraction images at 0.5° are on the same scale, directly comparable in size). Considering that extending back focus induces overcorrection, modifying an existing system to the aplanatic one would actually improve its axial correction, unless the system is undercorrected in its initial form. Reducing corrector-to-primary separation would gradually reintroduce coma, in proportion to the separation reduction.

● lower-order astigmatism P-V wavefront error for object at infinity is:

with the system astigmatism aberration coefficient as being the sum of the two individual mirror coefficients for the primary and secondary, as=a1+a2, with:

While generally low in the typical compact commercial SCT, astigmatism still requires attention. Relatively small design changes can result in significantly increased astigmatism level. For instance, typical f/2/10 SCT with spherical primary, σ1=0.4 and k=0.25 would, in an aplanatic arrangement, require secondary conic K2=-0.77 for cancelled coma; its astigmatic P-V error would have been W=-0.000155(αd)2. Change of the secondary magnification to m=4, corrector separation σ to 0.375 and relative marginal ray height on the secondary k to 0.3 (for identical back focus distance), would require zero-coma secondary conic K2=-1.176 and would have the P-V wavefront error of astigmatism W=-0.000374(αd)2 - greater by a factor of 2.4 (despite that, best image surface curvature would slightly improve, due to the lower Petzval curvature).

Graph at left shows the P-V wavefront error of coma and astigmatism in the typical 8-inch f/2/10 commercial SCT with spherical mirrors (both change in proportion to aperture diameter). Obviously, coma dominates, having nearly 4.5 times large P-V wavefront error at 1° off axis, and increasingly more toward inner field. For given eyepiece, the field size also changes in proportion to the aperture.

For comparison, coma in an f/10 paraboloid (dashed blue) is nearly five times smaller. Since the linear coma of a paraboloid changes with the 3rd power of focal ratio, the SCT linear field is, coma-wise, comparable to an f/6 paraboloid. Angularly, coma in a paraboloid changes with the square of focal ratio, thus the SCT field compares to that of an f/4.7 paraboloid. Specifically, the diffraction limited field radius in the SCT (only considering coma, but astigmatism is negligibly small at those field angles) is 2.5mm vs. 11.2mm in an f/10 paraboloid. Angular diffraction limited field radius in the SCT (4.3 arc minutes) is as many times smaller than that in the paraboloid, and equal to the diffraction limited field of an f/4.7 paraboloid.

Astigmatism in the SCT is only slightly stronger than in the comparable paraboloid, 1.6 vs. 1.4 wave P-V at 1° off axis. While this far off axis it equals coma in the paraboloid (as the P-V wavefront error), in the SCT is still only a small fraction of the coma wavefront error. It does not matter much in practical terms, since it is normally eyepiece astigmatism that dominates the outer field; it merely gets more distorted by coma in the SCT.

● field curvature; of interest are Petzval field curvature, which is not affected by the corrector and, thus, remains as for any two-mirror system, 1/RP=(2/R2)-(2/R1)=2(1-ρ)/ρR1, and best image surface curvature (or median astigmatic curvature) which is, in the presence of astigmatism, given by 1/Rm=(1/RP)+4as or: 

which for spherical mirrors (K1=K2=0) reduces to:

    Substituting for ρ in terms of m and k, with k=(1+η)/(m+1), the Petzval surface curvature can be also written as RP=(1+η)mR1/2[m2-1-(1+η)m] with the back focal length in units of primary's f.l. being η~0.5 for systems with f/2 primary.

     Graph below shows field curvatures for the typical 8-inch f/2/10 SCT with η=0.5, based on Eq. 118. Due to the difference in their astigmatism, a system with spherical mirrors has somewhat weaker, and aplanatic (w/aspherized secondary) somewhat stronger best image curvature than their Petzval. If the Petzval and astigmatism are of the same sign, they add up arithmetically to a stronger best image curvature, and they offset each other when of opposite sign, resulting in theee weaker median image curvature. Since the median surface is midway between the sagittal and tangential surface, with the tangential surface always 3 times farther away from the Petzval than sagittal (by 6a vs. 2a, a being the system astigmatism coefficient), median surface is flat when the astigmatism coefficient is one fourth of the Petzval value, and of opposite sign.

    While Petzval surface becomes flat with secondary magnification m~2, neither spherical-mirrors nor aplanatic (aspherized secondary) can have flat best image surface. It is weaker with lower secondary magnifications (i.e. with larger secondary), and is generally more curved in the aplanatic arrangement.

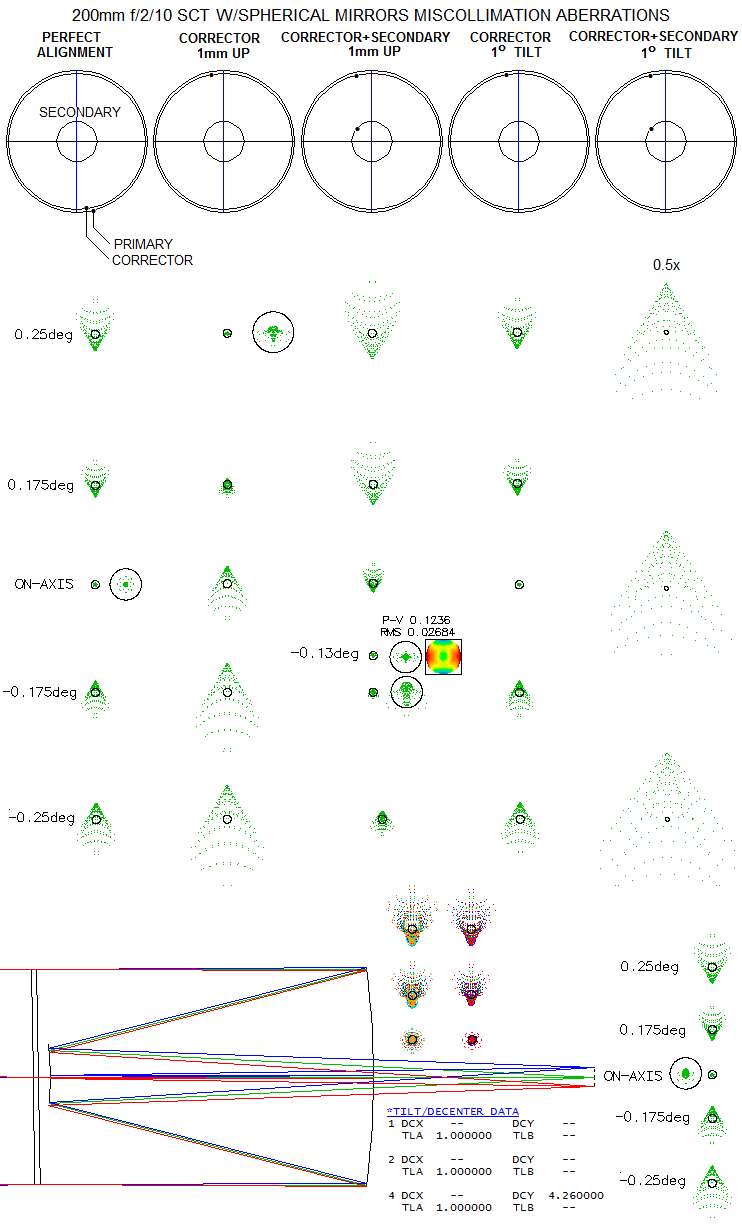
     Graph at right is a blown out shot of the graph at left, showing wider area with field curvatures for secondary magnifications below 2. Note that the green - aplanatic - plot apparently dives down toward flat surface due to the needed conic for coma correction raising to infinity for m=1 (flat secondary), and taking the curvature figure with it. In the actual system, the curvature bows back toward that for the primary with the stop at the corrector (similarly to that for the arrangement with spherical mirrors, only shifted toward lower secondary magnification). This is of little practical importance, since any practical secondary magnification is larger than 1.5.

In regard to misalignment sensitivity, the SCT, expectedly, has elements of both, two-mirror telescope and a Schmidt camera. In a typical SCT arrangement secondary mirror is mounted on the corrector. If they are centered with respect to each other, their decenter (i.e. lateral shift) with respect to the optical axis produces error of similar magnitude but of opposite sign on their two respective surfaces (Eq. 109 and Eq. 91.2 for the corrector and secondary, respectively), making Schmidt-Cassegrain with spherical mirrors less sensitive to small decenter errors. The effect is a relatively small shift of the best focus from the field center; some negligible residual astigmatism is also present. It can be illustrated on a raytracing example (below).

From left to right: (1) perfectly collimated system vs. one with (2)decentered corrector (that amounts to center misalignment of the corrector and secondary), (3) decentered corrector and secondary by the same amount, (4) tilt of the corrector alone, and (5) tilt of corrector and secondary together. It shows that decenter generates somewhat more of opposite in sign coma (primarily) on the secondary than on the corrector, with the best focus shifted from the physical field center - marked with ON-AXIS - by about 0.13° opposite to the decenter direction (note that physical field center deviates from the optical field center determined by the axial ray entering aperture; in this case optical center is little over 0.1° below the physical). Corrector tilt alone has no appreciable effect, but when it includes the secondary too, the effect is, for the same 1° tilt nothing short of disasterous (rightmost), with mainly coma, negative for counterclockwise tilt (shown, with light entering telescope from left to right), and positive for the clockwise tilt. As enourmously large as it is, this collimation aberration can be nearly entirely offset by decentering secondary by 4.26mm (bottom). Even the image tilt is corrected. It shows that even grossly misaligned SCT can act as well collimated. This, of course, implies that decenter error also can be offset by tilt.

Element tilt error always induces optical field center shift away from the physical center, as well as image tilt. In the case of mirrors, the shift angle is twice larger than the tilt angle, but it is not directly comparable to the field angle at the final image. This is due to the secondary field angle being magnified vs. primary field angle, here by about 3.4 times. Hence, if the original field angle at the final image is, say 0.5°, the actual angle of reflection for the central ray is 3.4 times larger, 1.7°. So the secondary tilt of 1° will induce angular optical field center shift corresponding to a little more than 0.5° in the final image field. But the coma generated at the secondary is commensurate to its physical tilt, i.e. for 1° tilt it will be at the level of coma at 1° off axis in a perfectly aligned system (over 7 waves P-V at the optical field center in this case; at the phisical field center, nearly 1/2 degree below the optical center, coma is over 10 waves). Coma at the optical field center is proportional to the tilt angle, which means that 0.1° secondary tilt would induce over 0.7 waves of coma at that field point. At the physical field center, however, the final magnitude is a sum of preexisting coma, astigmatism and the all-field coma induced at the secondary by its tilt; in this case, it is 3.7 waves P-V.

In an aplanatic SCT (K~-0.8 for conventional f/2/10 system) secondary mirror decenter induces more of coma, making it about three times more sensitive to decenter error. Also, there is no possibility to compensate for decenter error by adjusting secondary tilt; these systems have to be well centered.

Tilt of the corrector/secondary, due to a negligible error at the corrector, results in center field coma induced by the secondary, as given with Eq. 91.1. Again, in an SCT with spherical mirrors, due to the presence of system coma, at some point off-axis, in the direction of tilt, the two coma contributions will nearly cancel out, and the original field quality can be restored by making plane of the secondary parallel to that of the primary by tilting the former. Same applies to an aplanatic SCT.

Since coma due to tilt or lateral surface shift originates from surface deviation, it doesn't change with the field angle. It is added equally to the entire field, which leaves the field center with the amount of coma given by corresponding equations, while subtracting as much coma from one side of the field, and adding it to the other, in the orientation coinciding with that of the corrector's shift. As a result, best focus point shifts off center, in the direction where the misalignment coma is subtracted. The amount of shift depends on the level of SCT coma: in a typical 8" SCT with spherical mirrors, coma induced by as little as 0.2° tilt of the corrector/secondary approximately equals system's coma at 0.25° off-axis.

For larger SCTs with spherical mirrors, coma increases in proportion to the aperture diameter, and the shift angle per mm decreases accordingly. In an aplanatic SCT, there is no system coma, and both decentered and tilted corrector/secondary result in coma evenly distributed across the field. However, astigmatism is also present and it may be significant. In the Edge 8 model, 0.1° secondary tilt counterclockwise (top away from the primary) shifts optical field center about 1/20 degree above the physical center, with 0.9 waves P-V of coma in the former (slightly more at the physical center). At 0.4° off (0.45° from the physical center) coma and astigmatism are of similar magnitude, producing 1.2 waves P-V wavefront error miscollimation aberration.

Decentered secondary also induces image tilt, which can be significant in an aplanatic SCT (less so in the standard model, due to its field already compromised by strong coma), and can't be corrected by tilt-collimation.

Despace sensitivity of the SCT corrector is practically zero; since in practice it supports the secondary mirror, its axial shift would cause error appropriate to mirror decenter, as detailed in SCT focusing errors. Of course, any combination in misalignment of the two mirrors and corrector is possible. When compared to miscollimation aberrations in the classical and aplanatic Cassegrain there is an overall similarity.

A few words about Schmidt-Gregorian arrangement. In the arrangement with two spherical mirrors it can have coma cancelled with the corrector placed in the proximity of primary's focus (with the secondary protruding in front of it). That would make it even somewhat more compact that coma-corrected SCT, but the drawbacks of significantly stronger astigmatism and nearly doubled spherochromatism (due to contributions from the two mirror being of the same sign) make such a system less attractive.

 ◄ 10.2.2.4. Schmidt-Cassegrain telescope   ▐    10.2.2.4.2. SCT focusing errors ►

Home  |  Comments