|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
10.1.2. Field flattener
▐
11. FULL-APERTURE CORRECTORS
► 10.1.2. Sub-aperture corrector examples: Two-mirror systems
PAGE HIGHLIGHTS The most common two-mirror candidates for sub-aperture corrector are classical Cassegrain, Dall-Kirkham and Ritchey-Chretien. In addition, the simplest two-mirror arrangement, consisting of a pair of spherical mirrors, also can be made (very) useable with the addition of sub-aperture corrector. The two examples are Field's two-mirror telescope, using a single meniscus corrector, and Klevtsov, using two-element corrector to offset the aberrations of a pair of spherical mirrors. Sub-aperture corrector with two-mirror systems usually fills one of these two roles: it either serves as field corrector in systems that have good axial correction, or comes as an integral part of a system that cannot function without it. The former is usually referred to as field corrector, and the latter, somewhat informally, will be referred to as integrated (sub-aperture) corrector. The advantage of sub-aperture vs. full-aperture corrector is in much less glass required, also resulting in less added weight. The disadvantage is that they generally have more stringent tolerances for both, fabrication and alignment. The chromatism of a corrector is typically very low, and usually not a factor. Follow examples of common two-mirror systems with sub-aperture correctors: classical Cassegrain, Dall-Kirkham, Ritchey-Chretien, Field-Maksutov and Klevtsov.
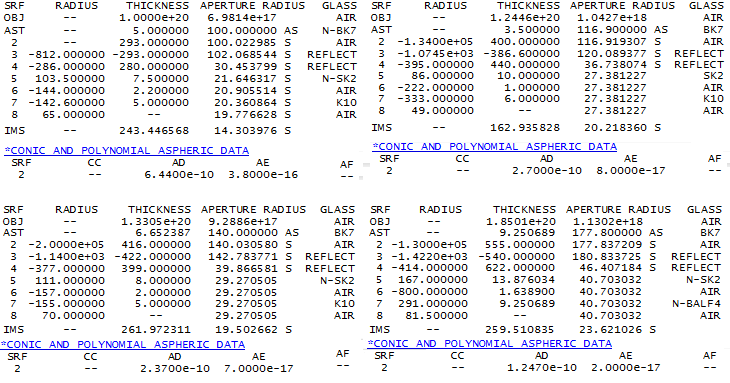
Sub-aperture correctors for classical Cassegrain In general, correcting field aberrations in classical Cassegrain, often with field curvature included, requires more or less simple two-element sub-aperture corrector. Depending on corrector's design, it can be either add-on field corrector, or integrated system corrector. Follow examples of both types. All four systems below are fast, or very fast for a Cassegrain, but have flat, well corrected fields. System A, published by Charles Rydel (SPECS), features two BK7 lenses, one plano-concave and the other bi-convex. System B, designed by Mike I. Jones (SPECS), uses two meniscus elements (FK5/BK7). Both these systems are classical Cassegrains that can function without field corrector. Unlike them, the last two systems with paraboloidal primary and spherical secondary, are useless without their integrated correctors. System C (SPECS) uses a Harmer-Wynne type corrector. System D (SPECS) uses three simple plano-convex/concave lenses in a very fast, well corrected arrangement.
For comparison, at 0.5° off-axis, coma blur in an f/10 classical Cassegrain w/o corrector would be three times the Airy disc diameter, and in an f/5.9 as much as 14 times larger than the Airy disc (0.82 and 3.7 waves P-V, respectively).
Sub-aperture correctors for Dall-Kirkham telescope Due to its spherical secondary and less aspherised primary, Dall-Kirkham (DK) telescope is easier to fabricate than any other all-reflecting two-mirror system. However, its relatively strong coma severely limits quality field already at medium focal ratios. A simple two-element sub-aperture corrector can effectively eliminate both, coma and field curvature. However, since such corrector induce under-correction, the primary is somewhat more strongly aspherised (still prolate ellipsoid). Thus these are integrated correctors. Also, DK with sub-aperture corrector is significantly more sensitive to misalignment. The DK correctors can come in various forms, but the three general configurations are: (1) a pair of plano-concave/convex lenses of identical reversed radii, (2) two meniscus lenses in () configuration, and (3) two meniscus lenses in )( configuration. Degree of correction is similar for all (meniscus correctors are likely to show smaller ray spots, but at that high level of correction it has little or no practical consequences).
Design A (SPECS) uses corrector made of two thin PCV/PCX BK7 lenses, for near-perfect overall correction. Corrector in the design B (SPECS) has advantage of being closer to the focal plane, thus using smaller lenses. On the other hand, lenses are more difficult to make. Design C (SPECS) is alternative to b, with the front meniscus replaced with biconvex lens, and D (SPECS) is the basic A design with a third, plano-concave lens added to correct lateral color. In general, the faster primary, the more aberrations generated at the secondary, and the harder it is to achieve high level of correction. The A sub-correctors for classical Cassegrain and DK are the simplest type, only requiring two plane surfaces and two identical reversed radii. Despite their apparent simplicity, needed calculation is quite complex. The focus is on coma, which requires establishing coma mirrors' aberration coefficient for the two mirrors - given by Eq. 82 as coma aberration coefficient, which determines the peak aberration coefficient as given by Eq. 13 - and finding at which corrector location it can be can be cancelled by the opposite coma induced by corrector, calculated from Eq. 98, with the effective aperture stop separation T for the corrector's front lens being the distance to the exit pupil formed by the secondary (measured from the pupil to the surface). With proper choice of lens radii and corrector location both, lower-order coma and astigmatism can be corrected. For flat astigmatism-free field, radius of the secondary needs to be sufficiently close to that of the primary (it varies somewhat, with the higher-order aberrations with fast/large systems shifting the optimum correction toward secondary with somewhat stronger radius than primary). As mentioned, primary conic is made somewhat stronger, to correct for under-correction induced by the lens corrector; the closer secondary r.o.c to that of the primary, the stronger primary conic is needed. The raytrace showed the presence of higher-order aberrations, which required additional radii/location adjustment, in order to have it minimized by balancing it with the lower-order form. Corrector's final parameters are the result of a lengthy series of iterations. The result is a modified Dall-Kirkham telescope with integrated sub-aperture lens corrector, and significantly improved field quality. Diffraction limited field in the green light typically approaches 1° in diameter on flat field, up to a dozen times, or more, greater than in a comparable all-reflecting Dall-Kirkham. Quality field is also up to several times greater than in a comparable all-reflecting classical Cassegrain, and significantly greater than in a comparable all-reflecting Ritchey-Chretien. Beyond 1° off-axis, or so, image often quickly deteriorates - more so than in the all-reflecting Dall-Kirkham, classical Cassegrain and Ritchey-Chretien - as a result of higher-order astigmatism and coma. That, however, has little importance since the field size is typically limited to about 1°, or less. Since the A and D arrangements are the easiest for fabrication, also allowing the entire system to be designed around a pair of COTS lenses, below are some additional details about them.
With both, 2- and 3-lens corrector, corrector location is determined by the relative strength of the secondary
vs. primary radius of curvature. The stronger secondary, the farther from it is the front corrector lens
(as astigmatism changes with the corrector separation)
and the lower primary conic is needed. Of course, stronger secondary is also smaller, i.e. farther away
from the primary, in order to keep the back focal length nearly unchanged. Coma is removed by giving to the
lenses' radius appropriate value. The f/8 2-lens corrector system above has the secondary significantly stronger
than primary, requiring -0.81 primary conic. If the two mirrors would have equal radii, for zero Petzval curvature
(neglecting the small amount induced by the corrector), the needed primary conic would reach -1.183, the
system becomes f/6.4, but the
overall correction remains excellent (below).
Sub-aperture corrector for the Ritchey-Chretien The two remaining aberration in the Ritchey-Chretien (RC) are astigmatism and field curvature. Astigmatism alone significantly limits quality field even over best (curved) image surface. Over flat field, it is further reduced by defocus resulting from field curvature. Neither aberration is significant in visual use. However, considering that the usual purpose of RC systems is imaging, some form of corrective action is necessary to improve quality of the outer field. Bending detector's surface to conform to best image curvature cancels out field curvature, but astigmatism still remains. Fortunately, correcting both aberrations is possible with relatively simple sub-aperture correctors. Since generating astigmatism by a lens corrector does not necessarily generate spherical aberration as well - such as the case with coma correctors - RC systems can use add-on field correctors for that purpose. Two examples are shown below.
System at left (SPECS) uses a pair of plano-concave and plano-convex lens of the same glass (BK7), designed by Richard from U.K. Lens elements have somewhat different surface radii, which is compensated for by widening the separation. Field correction is excellent, with the error in e-line being still only 0.068 wave RMS at the edge of 0.4-degree field radius. Color error is literally non-existent: as little as 0.01 wave RMS axially at 404nm and nearly half as much at 830nm. System at right (SPECS) uses two meniscus lenses, also BK7, for just as good, near-perfect correction: the e-line RMS wavefront error ranges from 0.017 on axis to 0.031 at 0.4° off-axis; axial color error is 0.068 wave RMS at 404nm, and 0.026 at 830nm, not changing appreciably over the entire field. The RC field can be satisfactorily corrected even with a single meniscus as an add-on corrector (i.e. w/o altering the original RC system). Here, at 0.4° off axis is still better than "diffraction-limited" (0.80 Strehl) in the green, with practically non-existent color error.
Meniscus thickness is rather flexible, and so is the separation from the focal plane (the meniscus extends focal length by less than 3%). Trace of residual coma can be eliminated by placing corrector little closer to the focal plane, but it would come at a cost of somewhat more astigmatism. Best overall correction is achievable with a trace of coma left in. The field has a higher-order astigmatism component, causing the best defined field to somewhat deviate from a plane, but the overall correction is still very good. Astigmatic field becomes more even and diminished in magnitude with larger focal plane separation, i.e. with the corrector closer to the primary. Meniscus can be thick enough to be made of two cemented plano-lenses.
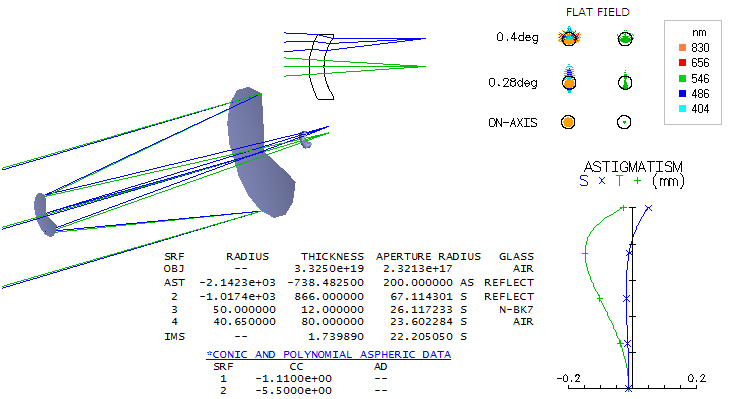
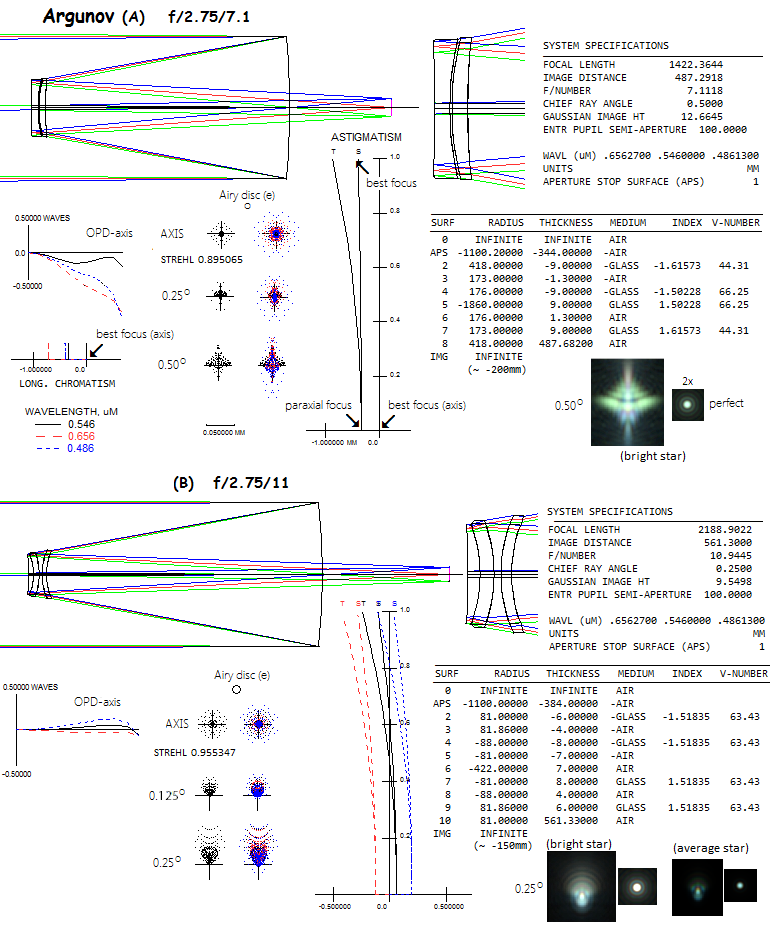
Argunov, Popov Particular form of a corrector, placed at the secondary mirror, was published as a complete analysis by Argunov in Russia, 1962 (about a decade later, similar arrangement was described in the U.S. by Richter, known as "Acme" telescope). It consists of an achromatized contact doublet whose rear surface is made reflective, serving as the secondary. Its limitation is relatively significant axial chromatism and, according to Klevtsov, hard to eradicate light scatter/ghosting. There is no published prescription, but a detailed analysis of the system is given in the articles by Argunov (USSR patent# 158697), which is the base of the Argunov-like system shown below (it uses LZOS glasses, OF3 and K2). It is a quite fast system, with the secondary spectrum more than 3 times smaller than in the comparable doublet achromat.
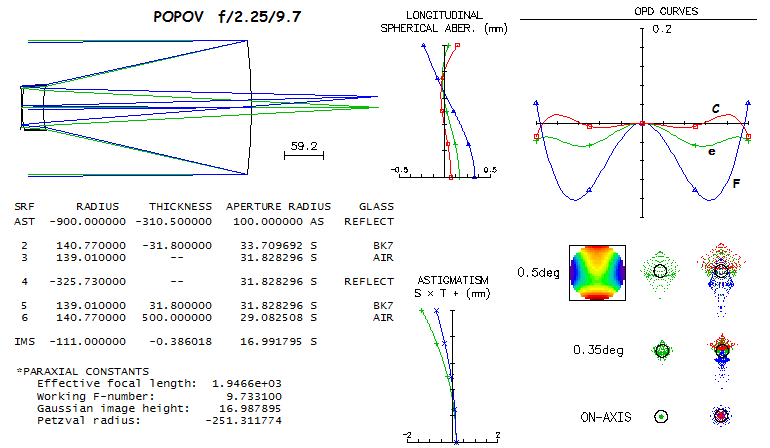
In 1966, Argunov came up with an advanced single-glass double-meniscus "isochromatic" (literally, "all colors equal") corrector. According to Klevtsov, it also has light scatter problem, and correcting the small residual coma requires corrector somewhat separated from the secondary. There is also no prescription available, so the system shown is to illustrate main characteristics of this arrangement; it uses LZOS glass, but replacing it with BK7 would not affect performance. Due to its strong radii, this corrector type requires meeting very tight tolerances. In 1966, Popov found solution for an aplanatic catadioptric telescope using a single thick meniscus in front of the secondary. System of this type is shown below. It has very good axial correction, good control of astigmatism, but strong field curvature and some lateral color.
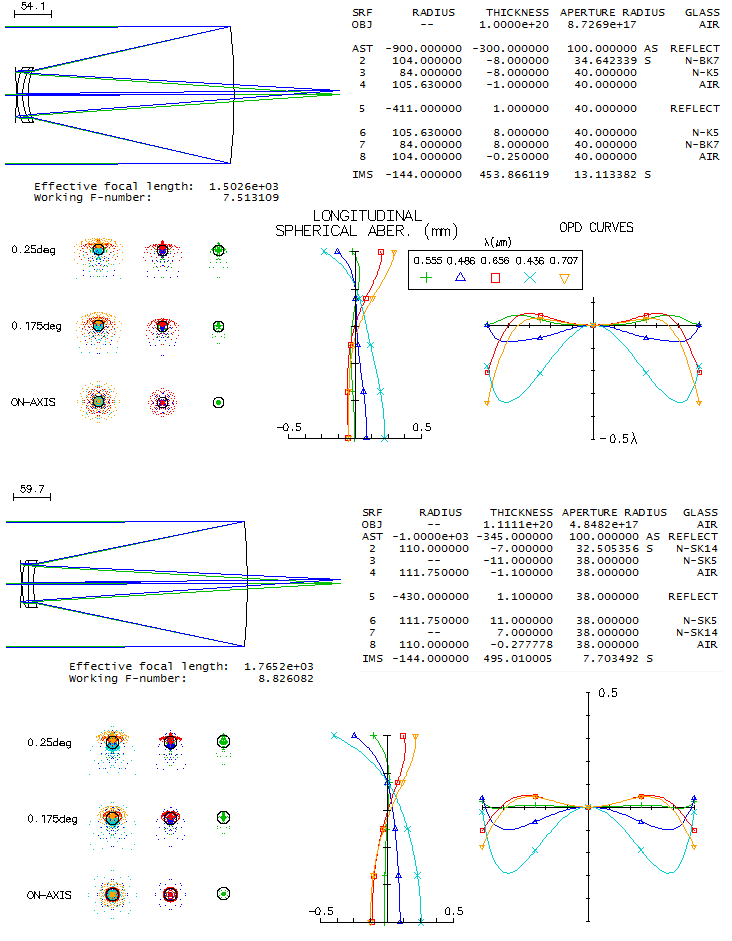
Other sub-aperture correctors for two-mirror system: Field-Maksutov, Klevtsov, Celestron Edge, Vixen VC200L A simple corrector for all-spherical two-mirror system would be the ultimate in convenience, since it would make aspherizing the mirrors unnecessary. Such correctors exist, but are less in use than full-aperture correctors for all-spherical systems. The reason is that, in general, they don't offer as good overall level of correction, and/or that their fabrication and alignment tolerances are significantly more stringent. It is particularly pronounced here, due to this particular corrector type having to correct an enormous amount of aberrations. Two examples of all-spherical two-mirror systems with integrated sub-aperture corrector are shown below (obviously, the corrector here must by integrated, since spherical mirrors alone would be entirely useless as a telescope).
Field-Maksutov (SPECS) mainly corrects for spherical aberration. The corrector offsets only a small fraction of primary's coma; with the secondary offsetting nearly half of it, the system as a whole has approximately half of the primary's coma, as angular wavefront aberration. Since the final linear field for given field angle is larger than that of the primary by the factor of secondary magnification m, the final linear diffraction-limited field radius is, from Eq. 70.2, approximated by mF13/45, or FF12/45 in mm, with F1 and F being the focal ratio of the primary and system, respectively. In this particular system, with F1=3, m=3.3 and F=10, diffraction limited field radius is little over 2mm. In that, this f/10 Field-Maksutov is nearly identical to a commercial f/2/10 SCT (SCT with an f/3 primary would, of course, have significantly less coma). Field-Maksutov coma is somewhat dependant on the meniscus thickness. In general, thicker meniscus offsets more of primary's coma, and vice versa, but the difference is not significant. In the above system, reducing meniscus thickness by 25% increases coma by about 10%. Placing aperture stop at the tube opening (as indicated above) nearly halves the astigmatism; however, since the coma is by far the dominant aberration, and not affected by stop position (the change in coma contribution by the spherical primary is nearly entirely offset by the opposite change at the corrector and secondary) the effect is relatively small: only about 4% reduction in the RMS wavefront error at 0.5° off-axis). Addition of the second lens in the Klevtsov design (SPECS) enables correction of both, coma and spherical aberration (f/3/10 system is rescaled version from Busack's PointSpread). However, corrector adds astigmatism, rising the total system astigmatism near to double that of the primary mirror. Still, field correction is significantly better than Field's, with the RMS wavefront error of astigmatism at 0.5° off axis being about 1/3 smaller (considering that astigmatism changes with the square of field radius, vs. coma changing with field radius, Klevtsov's field quality advantage is considerably greater than what the edge error implies). In addition, visual field in the Klevtsov should be further improved due to partial offset of its astigmatism with eyepiece astigmatism (in other words, visual field quality in the Klevtsov is limited by somewhat reduced astigmatism of the eyepiece). Coma in this type of arrangement also can be corrected with a cemented meniscus made of two similar glass types. Two examples are shown below, one with curved internal surfaces, the other with flat.
Central obstruction can be smaller, but it would result in still stronger best field curvature. These use nearly as fast primary as the commercial SCT, which makes them comparable. With a slower primary performance would improve. Relatively recent use for sub-aperture corrector has been found in the commercial SCT telescope as well. Specifically, it is the Celestron Edge line. While coma of this compact arrangement can be corrected by aspherizing the secondary, field curvature still remains, and can only be corrected by adding a field flattener. Since a pair of lenses can do both, correct for coma and field curvature, aspherizing the secondary becomes unnecessary. Examples below are based on the Celestron's published data (EdgeHD White Paper - Final). Since no specific prescription has been given in the paper, the systems shown are not the exact replica, but they are in every respect very close to the actual designs, and their performance level should be practically identical. There was no attempt to recreate the exact ray spot plots, only to make them similar, or very similar to those published.
Following section will concentrate on the Edge 8, but may
have implications for the entire series. Celestron's
Whitepaper on its Edge series doesn't specify type of
Schmidt corrector used, i.e. where is location of its neutral zone.
This is important piece of information with systems utilising Schmidt
corrector alone, because it determines level of spherochromatism. With
subaperture corrector present, they are both factors, and since we
don't have the specifications, we can only guess what the actual
spherochromatism level is. As it will be illustrated here, just the
ray spot plots are only a gross indicator. Ease of manufacture favors
corrector with 0.707 neutral zone. Coupling it with the system that is
a near exact copy of the published drawing produces a system that,
with the specified glasses, cannot be optimally corrected for
spherochromatisam and lateral
color at the same time. When spherochromatism is minimized, lateral
color is unacceptably large, as illustrated by the diffraction image
showing significant vertical smearing (#1, top; the five wavelengths,
average CCD sensitivity). Reducing lateral color
error is only possible at a price of increased spherochromatism; with
the colors crossing at 0.866 zone, lateral chromatism drops to negligible,
but spherochromatism is 2.5 times larger (#2). This, however, has a
potential marketing appeal, since the ray spot plots for non-optimized
wavelengths are smaller and clean (although the actual error is beter
indicated by the size of the dense spot area). The 80% encircled energy
radius is somewhat larger - 14.6 vs. 12.4 μ - but not significantly,
so it is a possible choice. Interestingly, the Edge 8 take by
Smith/Ceragioli/Berry starts with a profile shape with 0.866
neutral zone, and has roughly 50% larger lateral color error
than the 0.707 neutral zone profile with a crossing at 0.707 zone,
and much larger than this profile with crossing at 0.866 zone
- #1 and #2 described below, respectively - possibly because of a constraint to keep
crossing near 0.866 zone.
Discrepancy between chromatism and
lateral color correction lessens if the gap between lenses is minimized;
when reduced to 0.1mm, the crossing is brought just below 0.80 zone,
with the spherochromatism less than twice that at 0.707 zone (not shown).
In order to bring it down to the possible minimum, corrector shape needs
to be changed (#3, right). Needed Schmidt profile radius is -107,000mm,
with only small changes in the prescription vs. #1 (secondary r.o.c.
is -296, field corrector's R1 and R3 101 and -136.2, respectively,
primary-to-secondary -288.5 and AD 6.4e-10). New shape (short dashed)
is shown in comparison
to the 0.707 (solid) and 0.866 (long dashed) neutral zone shapes. It
requires more than twice more glass removed vs. 0.707 neutral zone
shape, but still less than the 0.866, which makes it acceptable in
practical terms. Expectedly, it has the smallest 80% EE radius at 14mm
off axis - practically identical to that in the e-line - significantly
smaller compared to the 0.866 neutral zone crossing (#2). Note that the
-107.000 radius value is for 0.1mm gap between the lenses. Since increasing
the gap pushes the color crossing higher, the greater gap, the
weaker radius term on the corrector needed for achieving optimum
color correction. Since radius value effectivelly adds defocus to
the P-V error of primary spherical at paraxial focus - described
by x4 - and best focus location has the two P-V errors
equal, and of opposite sign - profile described by x4-x2,
for which the radius term in this case is -82.000 -
the profile with -107.000 radius is described by x4-0.766x2,
hence with the neutral zone at (0.766/2)1/2=0.619,
all for the normalized aperture radius x values between 0 and 1.
Increasing the gap to 0.5mm, for instance, would require -177.000
radius term, i.e profile described by x4-0.463x2,
more than half way toward no radius term profile, described by x4.
This is why the Edge 8 with no radius term, given in the group of
four above, can have both, 0.707 zone color crossing and well corrected
lateral color (with the blue/violet slightly overcorrected). But it
would be much harder to fabricate, needing about 2.5 times more
glass removed than the 0.866 neutral zone profile, and six times
more than 0.707 neutral zone profile.
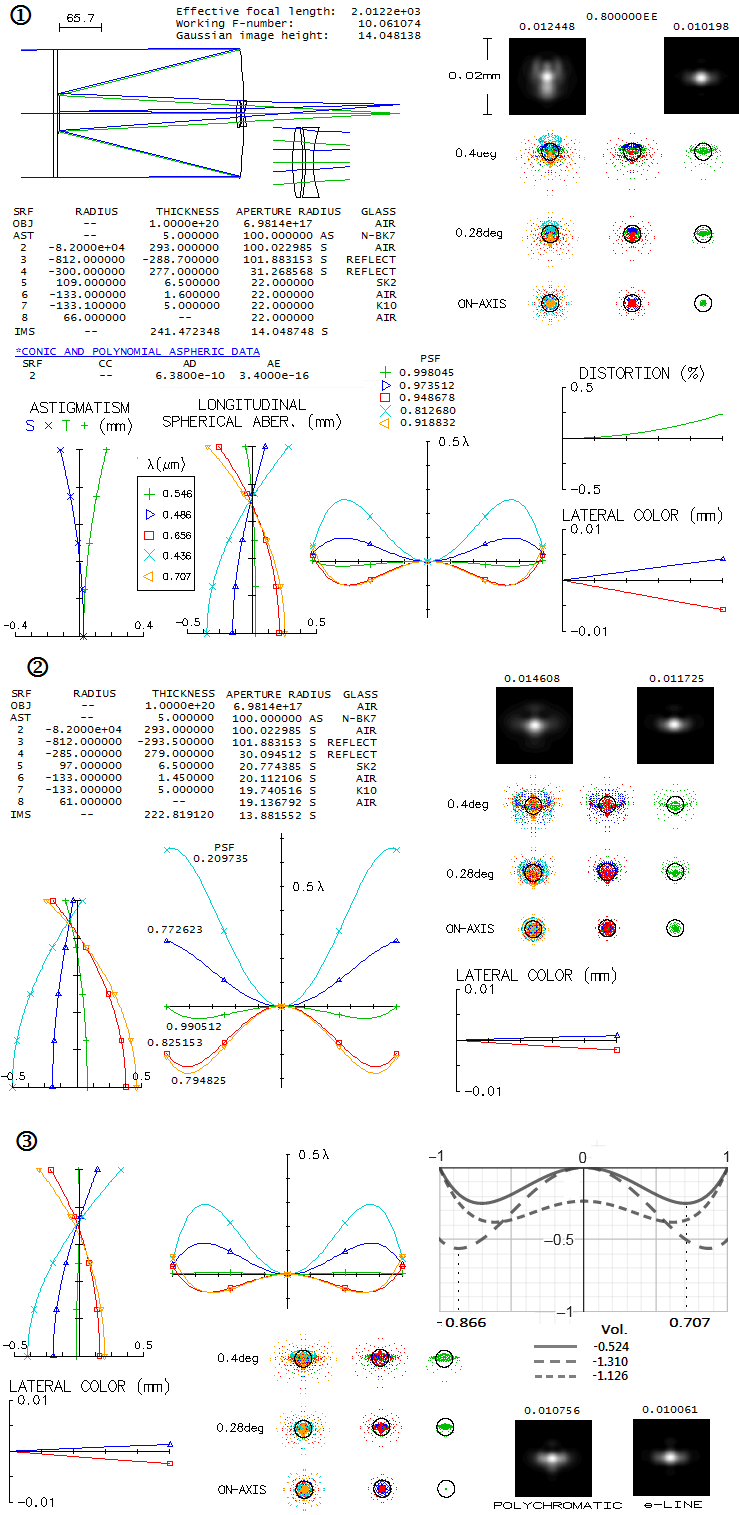
Coma and field curvature can be corrected with a similar corrector consisting of a pair of BK7 lenses, but the astigmatism is nearly twice greater. It implies that better correction might be possible with some other, more expensive glass combination, As mentioned, off axis error of these systems is already practically negligible, and added expense for the further improvement - if possible - probably wouldn't be justified. Vixen's VC200L VISAC, a 200mm f/9 system advertised as having primary with 6th order figure, uses 3-element sub-aperture corrector to achieve a highly corrected flat-field design. While its image contrast is somewhat compromised due to its 40% (linear) obstruction, correction level achievable with this design is exquisite. Technical drawing of the design can be found online, and suffice for reconstructing what is not strictly the actual design, but one that doesn't differ significantly in its level of correction.
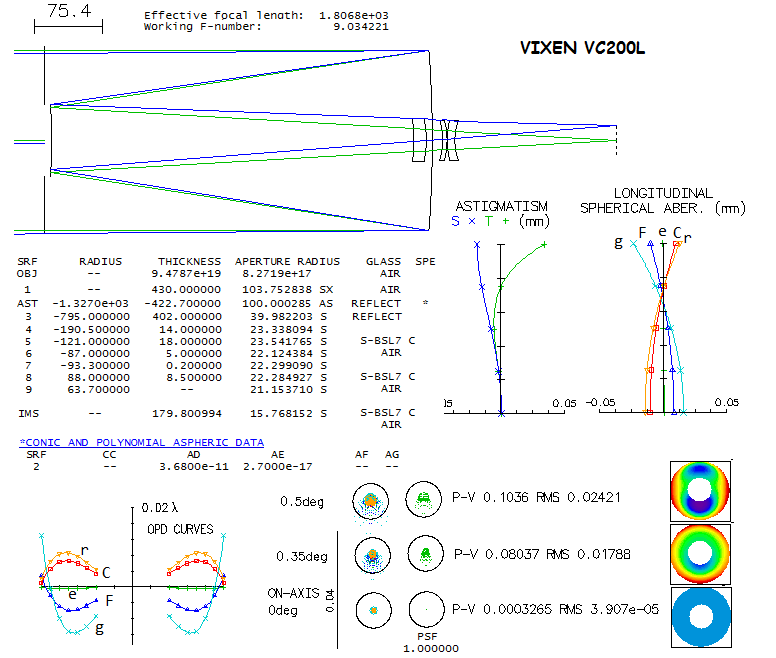
The violet g-line error is below 1/40 wave P-V, and the rest of lines have at least twice smaller error. Axial e-line Strehl 1.000000 is a rare sight indeed, and the polychromatic Strehl is 0.999+. The effect of central obstruction is analyzed in detail elsewhere. Of course, it is not to expect that the actual units offer this level of correction, but the design certainly does offer a realistic possibility to deliver "sensibly perfect" performance, as long as the aberrations are concerned. And so is unrealistic to expect the "6th order curve" on the primary, which in this case would require surface correction by 1/23 wave on its deepest point, at the edge (if corrected for 6th order spherical at its paraxial focus, from the product of the A6 coefficient and ρd6, with 0<ρ<1 and d the aperture radius; if corrected at its best focus, the curve added to the surface is described with ρ6-0.9ρ2 instead of ρ, and the deepest point is at the 77% zone, 1/50 wave P-V). Just by optimizing the 4th order curve by adding a tiny amount of overcorrection to minimize the higher-order component - which in this case translates into -0.69 conic, since the conic K relates to the 4th power coefficient as A4=Kd4/8R3 - the central line correction is still as good as 1/170 wave P-V, and the off axis correction remains practically identical. Ceravolo's all-spherical Gregorian
The original design is for 1m aperture with a very fast f/1.5 primary mirror. Design here is downscaled both, in aperture size and primary's
(and final) focal ratio, to make it more suitable for the amateurs' environment, and to make it comparable to other telescope types here
(it is, however, better suited to larger apertures, for better field quality, and for keeping central obstruction smaller). It consists of two
spherical mirrors and four small single lenses, yet its performance is comparable to that of the Celestron Edge systems, which in addition uses
a full aperture Schmidt corrector. The ray spot plots and diffraction images speak for themselves.
The disadvantage vs. SCT systems with as fast primary is its longer tube, although most of the extra
length could be limited to some form of extended secondary housing/baffle, making the O.T.A. less
balky. There would be, however, little diffrence in this respect vs. Cassegrain-Maksutov systems.
Schmidt sub-aperture corrector in a Gregorian
An
interesting idea from amateurs' circles can be used for larger and
faster systems. It places sub-aperture Schmidt corrector at the focus of
the primary, in the converging cone from the secondary. Therefore, it is
Gregorian arrangement with Schmidt corrector between two concave
mirrors. It allows for
spherical primary, but corrected coma still requires aspherizing the
secondary, although considerably less than in a comparable SCT. The corrector is
significantly stronger than the full-aperture version, but it is also
significantly smaller. Corrector's depth and amount of spherochromatism
induced are similar for both. The spherochromatism is nearly doubled
versus comparable SCT; since it changes inversely to the third power of
the primary's F-number, an ~f/2.4 primary would be necessary to reduce
spherochromatism in this system to the level of a commercial SCT of
similar aperture. Another option is making achromatic corrector, which
practically eliminates spherochromatism.
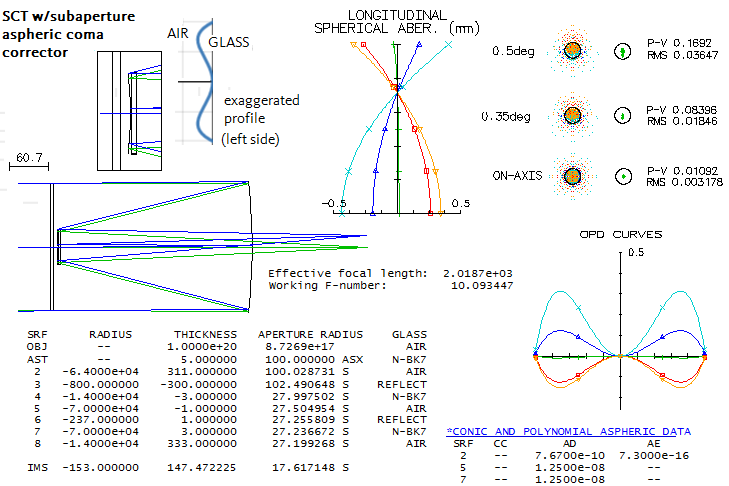
As shown to the left, chromatism is not intrusive in 8" aperture SGT with single-glass sub-aperture corrector (SPECS). It is at the level of 4" f/70 doublet achromat. Achromatizing it with a crown/flint combination with three identical Schmidt surfaces (the one on the flint element is inverse Schmidt surface) reduces spherochromatism several times, and may be desirable for larger apertures (SPECS). Further reduction of spherochromatism is possible with separated, much more strongly aspherised Schmidt elements. Since more strongly curved Schmidt surface also induces more of coma, a compact aplanatic Gregorian with both mirrors spherical can be achieved. As this advanced design by Mike I. Jones shows, the chromatism also has nearly vanished. The downside is over 50% greater astigmatism, and fabrication difficulty of a very strong double Schmidt corrector: in that respect, its stronger element is comparable to a corrector for ~f/0.5 standard Schmidt system. SCT with aspheric coma corrector A single lens can correct coma in a SCT with spherical mirrors. It can be done with a thin concentric meniscus placed at the inner end of the baffle tube, but it makes image curvature significantly stronger. But if a Schmidt-type plate is placed in front of the secondary, it can eliminate astigmatism and coma with image curvature at the level of aplanatic SCT. Image below shows a practical example in a 200mm f/10 system. Schmidt profile of the sub-aperture corrector is inversed, as illustrated, and on its other side is a mild radius, to bring the color crossing to the optimal 0.71 zone, while keeping both correctors with the neutral zone at the 71% radius, the easiest to manufacture. Depth of the subaperture corrector is 0.001mm, less than two waves. Spherochromatism remains at a level of the standard SCT. Since the sub-corrector lens induces undercorrection, the full-aperture corrector needs to be about 10% stronger. Extending focus induces about 0.06 wave P-V of undercorrection, and about 0.04 wave RMS of negative (tail down) coma per inch of extention. Field corrector for the standard SCT The standard SCT has significant uncorrected off axis coma and field curvature, as shown below (top; central obstruction is 35% linearly). Although more complex correctors can be used, a two-lens field corrector can eliminate both over fields wide enough for most purposes. Two such correctors will be considered here: a fairly well known design, consisting of a pair of meniscus lenses in a ")(" arrangement, and one consisting of a pair of simple plano-cv/cx lenses. Either corrector can be placed farther, or closer to the original focal plane, but the farther it is, the more of a spherical aberration residual it generates. So, while a relatively closely located corrector (~4 inch) can be used as an add-on, inducing acceptably low spherical aberration, those located at the primary, or - more so - in the baffle tube, have to be integrated by adjusting the Schmidt corrector power. Starting with the ")(" type corrector, located close enough to the image plane not to induce objectionable spherical aberration, optimized for 0.3° field radius (wider corrected field would likely have better edge correction, at a price of somewhat worse inner field correction). Some time ago Celestron announced unit(s) with this type of corrector placed in the baffle tube; it came to the prototype stage but then simply disappeard. Possible reason could be that they found it hard to meet required tolerances. Most of the aberration load, hence the correcting action, is on the negative (front) element, with the rear element making possible for small corrections in lateral color (front side) and coma (rear side). Front element is nearly neutral Petzval-curvature-wise, while the more uneven radii-wise rear element partly compensates for the strong negative Petzval value of the two mirrors combined. For the final flattening it is needed to induce positive astigmatism, which vary mainly with the corrector separation from the focal plane. Anyway, when placed closer to the focal plane, such corrector fully corrects for both, coma and field curvature, without introducing significant spherical aberration or astigmatism (middle). Small amount of undercorrection somewhat alters SCT spherochromatism, decreasing the error in the blue/violet, and increasing it in the red. Also, the crossing point shifts from the optimal 0.707 to ~0.65 zone, which somewhat increases the error in all unoptimized wavelengths (it effectively changes Λ value from 1 to ~0.85, hence increasing spherochromatic error by ~15%). This corrector a has weak negative power, increasing the final focal ratio to f/12. The menisci can be made thinner, without significant effect on the correction level (for instance, a 4mm thick BK7 pair at 390mm from the secondary, with -42/-38.5/35.5/28.5 radii, same lens separation, would give practically identical correction level; however, it has less of a negative power, with the final focal ratio being f/11.5).
Corrector consisting of a pair of simple plano-cv/cx BK7 lenses is as simple as it can be, and nearly
as good as the previous one over 0.3° field radius (boottom). The positive component has to be
slightly stronger in order to
minimize lateral color error, which results in a slightly faster final focal ratio. Despite being
closer to the focal plane, this arrangement induces more of spherical aberration, although still
acceptable assuming that the system has no inherent undercorrection error. Field flattener for the aplanatic SCT Other than spherochromatism, the only significant aberration remaining in a SCT made aplanatic (coma-free) by aspherizing its secondary is field curvature. About a third stronger than in the standard SCT, it is fairly strong. A simple split meniscus made of two glasses of somewhat different dispersion can flatten its field without indroducing significant aberrations. The meniscus has a weak negative power, resulting in the final f/10.8 focal ratio. The field is not perfectly flat on purpose, because the final flattening can only be done by further increasing astigmatism (by moving flattener 2mm closer to the secondary) which would improve correction over mid-field, but would worsen it toward the edge (ray spot plots in a box). According to the published spots, similar choice was made with Celestron's Edge, but it remains optional. Astigmatism is needed because Petzval curvature significantly differs from zero: the coefficient value of -0.02 is the 3rd order blur radius in mm due to the Petzval curvature (the minus sign means it is derived from a negative longitudinal aberration, i.e. implies surface concave toward corrector), is derived from the Petzval radius of -407mm and the f/10.8 focal ratio. Making the Petzval zero is possible (e.g. 44/0/24.2 radii, 7/3 thicknesses, N-SSK8/N-K5 at 456mm from the secondary), but does not appreciably improves correction, because astigmatism remains present. For most detectors the flatter field would be a better choice, since the astigmatic periphery would be left out. This flattener induces no appreciable spherical aberration, nor chromatism. It could be used with the standard SCT, where it would reduce field edge error bu some 15%, but the benefit is relatively small with the significant coma remaining (bottom). One negative is its strong rear radius, making the final converging cones in the outer field significantly diverging, which can negatively affect field correction of eyepieces. CONCLUSION Obviously, the aberration calculation is, in general, considerably more complex for sub-aperture lens corrector, as opposed to a full-aperture lens corrector, mainly as a result of displaced aperture stop, especially when more than a single element (e.g. single sub-aperture meniscus lens) is required. In principle, sub-aperture corrector is capable of correcting any single aberration. The difficulty arises from it tending to generate significant multiple aberrations, which may be difficult to match with the aberrations of the rest of the system. Often times, strongly curved surfaces are required, generating significant higher-order aberrations, and/or setting very tight fabrication/collimation tolerances. This is generally less of a problem with more relaxed radii-wise full-aperture correctors, which also can be used to manipulate main mirror's off-axis aberrations by varying the stop location. For that reason, most of quality catadioptric telescopes are made with full-aperture correctors, despite their often higher cost. To those most common in amateur telescopes will be given consideration in the following pages.
|