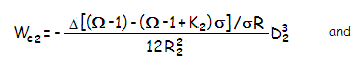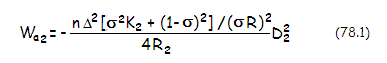|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
8.1.3. Newtonian reflector diagonal flat
▐
8.2.1. General aberrations
► 8.2. All-reflecting two-mirror telescopesAberrations - Classical and aplanatic - Dall-Kirkham - Loveday - Miscollimation and close focusing
PAGE HIGHLIGHTS As the title implies, this section as about mirror-only telescope systems. Mirror/lens systems are presented in section 10. Catadioptric telescopes.
While the Newtonian does use a pair of
mirrors, one of them is flat and, therefore, a passive imaging element.
Systems with both mirrors active in shaping up the wavefront - in other
words, with both mirrors curved - are termed two-mirror telescopes.
Classical two-mirror arrangements are Gregorian -
the very first reflective
telescope design, conceived by James Gregory in 1663 - and
Cassegrain (FIG. 121),
probably introduced in 1672 by Laurent Cassegrain. In the former,
concave secondary mirror is placed outside the focal point of the
primary mirror, and in the latter the secondary is convex, placed inside
the primary mirror focus. In either case, the final focus is made
accessible either by focusing through an opening on the primary, or by
inserting small diagonal flat in front of it, to reflect converging cone out to
the side (Nasmyth arrangement).
The final system focal length,
is determined by the focal lengths and separation of the two mirrors. It determines secondary magnification as
where f1 and f2 are the focal length of the primary and secondary mirror, respectively, and s is the mirror separation. According to the above relation, for light moving from left to right the final system focal length is numerically positive in the Cassegrain, and negative in the Gregorian. Primary mirror focal length (f1) is always negative, while the secondary mirror focal length f2 is positive in the Gregorian arrangement, and negative in the Cassegrain; mirror separation s is negative for both. In order to correct for spherical aberration, the two mirror must have specific conic forms. Although Gregory established - based on conic properties established by Rene Descartes (La Geometrie, 1637) - that in his arrangement primary and secondary need to be paraboloid and ellipsoid, neither him, nor anyone else at the time knew how to make aspheric surfaces. For some time, it was difficult to produce even spherical mirrors accurately. As a result, early instruments were suffering from all of the three primary "image quality" aberrations - spherical, coma and astigmatism. It took about half a century for mirror making to advance to that next level, when John Hadley, in 1720, built first two-mirror system close to its theoretical specifications. It eliminated most of spherical aberration. Not long after, James Short was the first to make a true Gregorian system, with paraboloidal primary and ellipsoidal secondary. He went on to produce well over a thousand Gregorian telescopes. Due to the added difficulty of making strongly aspheric convex surface (hyperboloid) for the secondary, the Cassegrain was the last to come into efficient use, but soon became the most popular two-mirror arrangement. First significant telescope of this type was probably James Nasmyth's 20-inch in 1845. Two-mirror systems using paraboloidal primary are termed classical Cassegrain (w/convex secondary), or Gregorian (concave secondary). Nowadays, unlike the telescope pioneers, we can determine lower-order aberrations of such a system at the best focus location with a few simple relations. The system aberration is a sum of aberrations at the primary and secondary mirror. For the former, the P-V wavefront error at the best focus for object at infinity is, from Eq. 7, 12 and 18, given by:
for spherical aberration, coma and astigmatism, respectively, with K1 being the primary conic, D1 the aperture diameter, F1 the primary's focal ratio, α the field angle, h the height in the focal plane and f1 the primary's focal length. For the secondary, the effect of close object distance and displaced aperture stop make the aberration relations more complex. Change in stop position doesn't affect the coefficient for lower-order spherical, but the object distance does; thus Eq. 9.1. applies (note that 2ψ=Ω). With coma, both stop separation and object distance affect the aberration coefficient, thus the appropriate expression is Eq. 15.3. And with astigmatism, stop separation affects the coefficient, but object distance doesn't, as given with Eq. 22. Substituting these coefficients in their respective wavefront aberration functions which are, same as for the primary, given by Eq. 7, 12 and 18, results in the following P-V wavefront error at the best focus for spherical aberration, coma and astigmatism, respectively:
with Δ being the chief ray heght at the secondary, K2 being the secondary conic, D2 the secondary minimum aperture (the cone width at the secondary), R2 the secondary radius of curvature, Ω the inverse of the secondary's surface-to-object distance ℓ in units of its radius of curvature (Ω=R2/ℓ, see FIG. 121, bottom), and σ the secondary to the aperture stop (i.e. primary) separation in units of secondary's radius of curvature (according to the sign convention, σ is numerically negative in Cassegrain, while positive in the Gregorian, and Ω is positive in both). Some useful identities are (Ω-1)=(m+1)/(m-1)=(2ρ/k)-1, with k being the relative height of marginal ray at the secondary in units of the aperture radius, and ρ=R2/R1, the secondary radius of curvature in units of the primary's (both parameters extensively used on the next page). The system P-V wavefront error at the best focus for each aberration is given by a sum W=W1+W2. From their equations, it can be seen that the change in stop positon - i.e. placing stop at some distance from the primary - will have little effect on either coma or astigmatism at the secondary. With coma, object distance (image by primary) is independent of stop position, change in the chief ray height is generally small, and stop separation parameter in both, numerator and denominator tend to offset one another. It is similar with astigmatism. Picture below shows ray geometry for stop at the prmary vs. stop at primary's focus. With the former, coma at the secondary results from both, angle of incidence and decenter. With the latter it is only decenter causing it, since all chief rays pass through the primary focus and reflect onto secondary parallel with the axis (since the aperture stop for the secondary is the image of the actual stop formed by the primary, in this specific case at infnity; note that the light cones around chief rays still converge toward points forming the image by primary). In general, the effect of stop shift is similar in two mirror systems using corrective lenses. It is implied by Eq. 78-78.1 that with paraboloidal primary, secondary conic for corrected spherical aberration is K2=-(1-Ω)2. Spherical secondary has coma of opposite sign to that of the primary in both, Cassegrain and Gregorian, but significantly smaller; aspherizing it to correct for spherical aberration adds additional offset and lowers the system coma to the level of a comparable paraboloid. Astigmatism of spherical secondary is, on the other hand, of opposite sign to that of the primary in the Cassegrain, and of the same sign in Gregorian; aspherizing it for corrected spherical adds astigmatism of the opposite sign in both, resulting in the two ending at a similar system astigmatism levels. As the astigmatism relation in Eq. 78.1 shows, it is independent of object (i.e. primary's image) distance. According to Eq. 78-78.1, needed secondary mirror conic for zero coma is σK2=-(R22D13/R12D23)-(1-Ω)(1-σ), and the corresponding conic for the primary (to compensate for spherical aberration induced by changing the secondary conic), K1=-1-[K2+(1-Ω)2]R13D24/R23D14. Alternately, needed mirror conics in terms of the primary and system focal lengths, and mirror separation are given as K1=-1, K2=-[(f-f1)/(f+f1)]2, and K1=-1-2(f1-s)f12/sf2, K2=-[(f-f1)/(f+f1)]2-2ff13/s(f+f1)3 for the classical and aplanatic arrangement, respectively. Note that the primary focal length f1 and mirror separation s are always numerically negative, while the system focal length f is numerically positive for the Cassegrain, and negative for the Gregorian. The next step in two-mirror system evolution was modifying mirror conics for the correction of coma, in order to obtain wider well corrected photographic field. Coma-free two-mirror systems are termed aplanatic Cassegrain (Ritchey-Chretien) and Gregorian. A two-mirror system interesting from the practical point of view is Dall-Kirkham, consisting of ellipsoidal primary and spherical secondary.
Two-mirror arrangement
worth mentioning is the Gregorian with three reflections,
which can be made anastigmatic aplanat (corrected for primary
spherical aberration, coma and astigmatism).
Front baffle tube
Although formally not a part of their
optical system, axially configured two-mirror telescopes regularly use
baffle tube in front of the primary, as well as baffle tube around
secondary, to protect the final image from
stray light.
T=(1+η)/[m+(1/o)]
where η is the back focal length B in units of primary's
f.l. and o is the relative size of central obstruction in units
of the aperture (o=S/P).
Obviously, the distance from this plane to
the final focus is a sum of its separation from the primary L and
back focal length B. Since L+B=FT, with F being the final
system focal ratio, L=FT-B. Substituting in this relation
T=(1+η)P/(m+1/o) and dividing with f1
- the primary focal length - gives the
limit to the front baffle extension in dimensionless parameters, measured from the primary, in units of
the primary mirror f.l. as:
where ε=L/f1.
As mentioned, the width of the cone converging from the secondary at this point equals the
hollow core diameter in the axial cone converging from the primary,
caused by obstruction,
given by
in units of the primary mirror diameter. At this baffle position, field
of full illumination is limited to the axial spot. Moreover, baffle tube
won't protrude into the light converging from primary only if with zero
wall thickness (assuming its inner diameter equaling T, in order
to allow all axial light from the secondary to pass through). Thus, the
front opening of an actual front baffle tube will have to be pulled
somewhat toward primary, to avoid light intrusion. Since the inner
hollow cone converging from the primary has the effective focal ratio Fc=F1/o,
with F1
being the primary's focal ratio, every mm of shortening the front baffle
tube clears 1/2Fc
mm for the baffle wall thickness. So, if baffle wall at the opening is
1mm thick, baffle tube extension should be a bit more than 2Fc
mm shorter than what Eq. 79 implies.
This will also create some "breathing room" between
baffle opening and cone converging from the secondary. For instance, a
system with f/3 primary
(F1=3)
and P/3 central obstruction diameter (o=0.33), will have Fc=9
and need some 10mm shorter front baffle tube. If the secondary
magnification is 4 (so F=12), that will create 10/2F=0.4mm gap between
the converging cone and inner edge of the baffle opening. As
SCT systems show, such tight front
baffle opening causes negligible vignetting (of more concern is the rear
baffle tube opening).
This baffle gap g will also create a
small 100% illuminated image field radius i100,
which is well approximated with i100~(f1+B)g/(f1-L)
or, in dimensionless units, i100~(1+η)g/(1-ε).
Pulling the front opening closer to the primary would create wider gap,
and increase 100% illuminated field, but would likely require increase
in the secondary baffle diameter, i.e. central obstruction. The two
baffles, around secondary and in front of primary have to work in
concert, i.e. have to be tightened so that no ray passing next to the
secondary baffle pass the baffle tube and fall directly onto the image.
For that to happen, a ray projected from the bottom of baffle tube rear
opening, that touches top of its front opening, is not allowed to clear
the secondary baffle. For that to occur, opening of the secondary baffle
has to be at a distance d from the rear baffle tube opening
not exceeding:
d=H/[2F1b+1],
preferably a bit smaller, where H=f1+E,
with E being the length of baffle tube behind the primary, and
b is the ratio of baffle tube opening vs. length.
Since the position of this plane determines the width
of cone converging from primary, it also determines the minimum needed
central obstruction. If the secondary is already larger, the two baffles
will be well matched. If, however, the secondary is smaller than the
width of this cone cross section, secondary baffle and corresponding
central obstruction need to be larger.
If the secondary - i.e. its cell - is larger than
this cross section, the baffle should extend toward primary by
Rear baffle tube effect on image field
Unlike front end baffles which only vignette image field, rear
baffle tube opening also sets the limit to its size. Image below - a
raytrace drawing of an actual Cassegrain system - illustrates
geometry of rays, reflected from the secondary into the baffle tube,
and exiting toward final image on its opposite end. As shown on
a SCT system,
vignetting on the secondary baffle is generally negligible,
front baffle tube opening limits the fully illuminated field and,
in general, field for imaging applications, while rear baffle
opening limits the visual field size. As field angle increases,
the narrow converging cones at the rear baffle opening are
increasingly trimmed off at the rear end, and ultimately completely
cut off from reaching image space.
Loss of one magnitude (60% light loss) is generally acceptable
for the very edge of visual field. When the center of converging
cone is on the baffle edge, as shown (blue footprint), loss of
light is just below 50%. The angle will vary with the system,
but the corresponding linear field size is determined by the
rear end clear radius and its separation L from the final
image. Knowing that the chief ray angle incident on the secondary
for most systems is 3 to 3.5 times (3 to 5 secondary magnification,
respectively, with 0.25D minimum secondary size, D being the aperture
diameter) larger than initially, on the primary, means this added
field height a is approximated by 3.3αL, with the
initial incident angle α given by α=d/S, and
d being approximately b/4.5 (since the secondary to baffle
rear end separation is somewhat larger than secondary-to-primary).
For, say, b=12.5mm and S=400mm, d~2.8mm and, with L=100mm, the added
image height is a~330(2.8/400)~2.3mm, for about 15mm visual field radius.
More detailed take on vignetting at the baffle end is given on
image below. Top graph shows how illumination - given as overlapping
area of two circles, one representing baffle end opening, and the other
converging beam in that plane - changes with the relative size of
converging beam for two cases: (1) with the opening containing full radius
of the converging beam, y1, and (2) containing 3/4 of
its diameter, y2. For
practical beam values, roughly between 0.2 and 0.5 of the opening
diameter, the difference is near negligible.
Bottom graph shows how illumination falls with the increase in center
separation between the opening and beam circle, for the latter being
1/2 and 1/4 of the opening diameter. Neglecting vignetting
at the front end, the smaller beam would produce larger fully illuminated
field, but would have a faster illumination fall-off once it starts.
The two would have about equal visual field size (defined as limited
by 1 magnitude illumination drop), but the bigger beam would produce
larger low illuminated field.
◄
8.1.3. Newtonian reflector diagonal flat
▐
8.2.1. General aberrations
► |
FIGURE
121:
Front
baffle tube should be extended forward from the primary as much as
possible, not to intrude into the light converging from the primary. As
illustration at left shows, the limit is set by the plane where diameter
of the cone converging from the secondary equals diameter of the hollow
core (caused by obscuration by the secondary) in the cone converging
from the primary. The common diameter, in units of the aperture diameter
P, is given as:
