|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
8.2.4. Dall-Kirkham telescope
▐
8.2.6. Miscollimation, close focusing
► 8.2.5. Unusual two-mirror systems: Loveday, Eisenberg-Pearson, Schwarzschild, Couder
PAGE HIGHLIGHTS Two-mirror systems can be modified so that the secondary reflects light back to the primary mirror, with the final focus forming after this last, third reflection. Best known system of this kind is Loveday-Cassegrain, using a pair of confocal paraboloids (Mersenne arrangement). After the third reflection (the second from the primary) the final focus is formed beyond the secondary. Coma is identical to that in a comparable Cassegrain, while the astigmatism is smaller by a factor of (m2+η)/(1+η)km2, resulting in lower field curvature as well. By aspherizing the mirrors somewhat more, systems corrected for either coma or both, coma and astigmatism can be obtained. In the Cassegrain configuration, however, design constraints impose severe limits to the useable field size, with the added drawback of relatively large effective central obstruction. In the Gregorian arrangement, while the central obstruction remains relatively large, much wider fields are possible, with the only remaining aberration being field curvature (FIG. 125). Such system was, to my knowledge - credit to Mr. Charles Rydel, President of the Commission des Instruments of the Societe Astronomique de France -first described by Shaffer.
FIGURE 125: Two-mirror 3-reflection system in the Gregorian arrangement. Concave secondary mirror (S) reflects light back to the primary (P), which then forms the final focus through an opening on the secondary. Correction of all three primary point-image aberrations, spherical, coma and astigmatism is possible with ellipsoidal primary and hyperboloidal secondary mirror. The only remaining aberration is a relatively strong field curvature. The final system's focal ratio F is larger by nearly 1/3 than focal ratio of the primary. Originally, the arrangement was first published by Shaffer, but somewhat better corrected systems of this kind are achievable. These systems are effectively three-mirror systems, and aberration coefficients are more complicated. It would suffice here to give a working prescription. Relative system parameters (units of the primary radius of curvature) of the Gregorian two-mirror 3-reflection anastigmatic aplanat are very simple:
S/R1 = 0.7248 S being the primary-to-secondary separation, R1 and R2 the primary and secondary radius of curvature, respectively, K1 and K2 the primary and secondary conic, respectively, and Rp the Petzval (image) curvature which, in the absence of astigmatism, coincides with best image surface. These parameters are nearly optimized for an f/3 system; they are scalable by either aperture, or primary's F-number. Scaling by the aperture doesn't require any changes, while slower system require slightly stronger secondary conic to optimally re-balance spherical aberration.
All aberrations - except field curvature - are well corrected.
Axial correction for 400mm f/3 system is 0.04 wave RMS of balanced
higher-order spherical, with the balanced higher-order coma limiting
diffraction limited field to 0.6°
radius (with 50% linear central obstruction, the field size limit is about 1.5 degree in diameter. Higher order spherical aberration increases inversely to the 6th
power of focal ratio, limiting the focal ratio at this aperture size to
~f/2.7 for diffraction limited axial correction.
Field curvature is strong, requiring
either curved detector or field flattener. The simplest flattener form, a
singlet positive plano-convex lens with the front surface radius
R=(1-1/n)Rp
=0.15(1-1/n)R1
,
(the actual radius should be about 10% stronger, since the flat side
induces roughly 10% as much astigmatism of opposite sign; better correction, however,
gives biconvex lens slightly weaker in power than what is indicated by the equation) with small compensatory changes in the conics
to optimize for coma and spherical, achieves good correction, except for
lateral color. Its correction requires adding at least one more glass
element, which can be as simple as a meniscus of equal radii in front of
the field flattener. Plot below shows spots for such combination with
the last glass surface 1.8 mm from the image, for 430-700nm range.
Correction in the green is not significantly worse than in the
all-reflecting arrangement, with the residual secondary spectrum being the
primary source of chromatic error. Nearly eliminating chromatic error
would require achromatizing one of the elements; also, somewhat more
complex corrector is needed for larger corrector-to-image separation.
Correction level of this arrangement is somewhat better than in the original
Shaffer arrangement (R2
=S=0.75
R1,
K1=-0.405,
K2=-6.04),
which has similar correction level at 40% smaller aperture
and ~f//3.5.
Somewhat different take on the two-mirror 3-reflection configuration
is the Eisenberg-Pearson
In this simple system, it is not possible to flatten field by
changing mirror parameters. A quick attempt showed that a simple zero-power flattener
consisting of a pair of singlets, planoconcave
followed by a planoconvex (both BK7, 222mm radius, placed at 440mm from the
primary, facing it with their flat side) flattens the field with no
significnt aberrations induced. Better correction without a
field corrector is attainable
if the third reflection comes of a surface that has different
conic from that of the primary. The field is perfectly flat,
and there is no aberrations to speak about (bottom). It does
require stronger aspherics, and the central portion of the
primary is a significantly stronger hyperboloid than the outer
primary area. Since the stronger hyperboloid is flatter, with a
smaller sagita, having these two hyperboloids share the same
vertex - as in this prescription - means that the edges of the
inner hyperboloid would be carved into the outer one
(the depth is roughly 1/100 of a mm).
Another unusual astrographic system consists from two concave mirrors,
with the secondary inside the focus of the primary FIG. 126). It
was derived by Karl Schwarzschild as a solution for two-mirror system
with best correction of aberrations possible. Schwarzschild found that a
two-mirror system can correct only four Siedel
aberrations: the remaining one is either field curvature, or
astigmatism. The variant with astigmatism as the only remaining
aberration
is usually referred to as Schwarzschild telescope, and the
alternative with no astigmatism but with curved image field is known
as Couder telescope.
In the former, the minimum relative size of the secondary (in units of
aperture diameter) k needs to be related
to the secondary magnification m as k=(1-m-m2)/(1-m2)=1-m/(1-m2).
This implies that m has to be smaller than 1 for k<1, i.e. for
the secondary smaller than primary. Unavoidably, the final focus falls
in between two mirrors. Also, m<1 implies that the secondary is concave.
For the maximum acceptable secondary size of k~0.5, the corresponding
secondary magnification, from m=[(4k2-8k+5)0.5-1]/2(1-k),
is m~0.4. Larger secondary magnifications require smaller secondary, but
secondary size reduction is limited by image accessibility.
On the other hand, due to the wide primary-to secondary separation,
needed secondary size to keep the outer field well illuminated becomes
excessive at k~0.5; in the above system keeping 2-degree field fully
illuminated would require clear secondary mirror surface diameter of
nearly 2/3 of the full aperture, and the effective obstruction almost
certainly exceeding 70% of the aperture diameter. Thus the practical
secondary magnifications value cannot deviate significantly from m~0.45
k~0.44 level.
With k and m determined, mirror conics can be obtained from
Eq. 86-87. After
substituting for k, the conic relations become:
K1
= -[2(1-m-m2)+m3]/m3
and
K2
= (1-m)(1-m2)/(1-m)3
For viable level of secondary magnifications m~0.45,
the corresponding mirror conics are K1<-8.6
and K2>2.1
for the secondary.
As with all two-mirror systems, the secondary mirror
radius of curvature is given by R2=ρR1,
with ρ=mk/(m-1).
The field is flat, but the astigmatism-cancelling field curvature limits
quality field size. Since the secondary contributes nearly as much of
astigmatism as the primary, the system astigmatism is approximated by
double that of the primary, thus as the P-V wavefront error W~(αD)2/2R,
where α is
the field angle in radians, D the aperture diameter and R
the mirror radius of curvature (for lower-order astigmatism, RMS
wavefront error is smaller than the P-V by a factor 241/2).
In the Couder curved-field anastigmatic aplanat, k=1-2m, hence the
maximum secondary magnification is lower than in the flat-field aplanat.
Needed mirror conics are:
K1
= -(m3-2m+1)/m3
and
K2
= (m3+m2-m)/(1-m)3
For k~0.5 or smaller, the corresponding secondary magnification is
m~0.25, or larger. Again, image accessibility requirements limit
reduction of the secondary size to about a third of the primary mirror.
Since at m~0.25 and k~0.5 needed secondary size to prevent vignetting of
the outer field becomes excessive, the secondary magnification is
confined to a narrow range around m~0.3 and k~0.4. The corresponding
mirror conics are K1~-16
and K2~-0.5,
respectively. In general, the primary is more strongly aspherised than
in the Schwarzschild telescope, while the secondary becomes a mild
prolate ellipsoid. From the fabrication point of view, the twice more
strongly aspherised primary is mainly offset by switching to the prolate
ellipsoid secondary. However, the drawback is significantly lower
practical secondary magnification, potentiating the image accessibility
problem.
With zero astigmatism, the image curvature equals system's
Petzval radius of curvature, given as:
RP = mkR/2(m-1-mk),
with R being, as before, primary's radius of curvature. For, say,
m=0.3 and k=0.4, field curvature is R/-13.7, remaining strong with the largest R values that meet practical requirements for system
length. For the above 200mm f/10/3
Couder telescope, the corresponding image curvature is Rc=RP=-293mm.
At 1° off-axis, it would induce as much as
4.8 waves P-V (1.4 wave RMS) wavefront error of defocus. Clearly, curved
detector surface matching the image curvature, or a field flattener
lens, is a must.
Similarly to the Schwarzschild system, residual higher-order spherical
aberration - only about half as large - can be corrected by extending the
secondary radius of curvature by about 1% (it also minimizes residual
higher-order coma, but it was already negligible).
With larger/faster systems, the higher-order residuals grow
exponentially.
While this type of two-mirror system can achieve
very good correction, it also has several potential drawbacks which,
combined, probably prevented
its more widespread use.
A simpler version of the cross-axis three-mirror system is a
cross-axis Gregorian. Decades ago I thought
I invented it, but little later found out that it was already known and probably patented by someone (not
sure of the name, something like Johnson, but search doesn't return any results now). The unique property
of this arrangement is that central obstruction size is directly related to the field size, i.e. it can
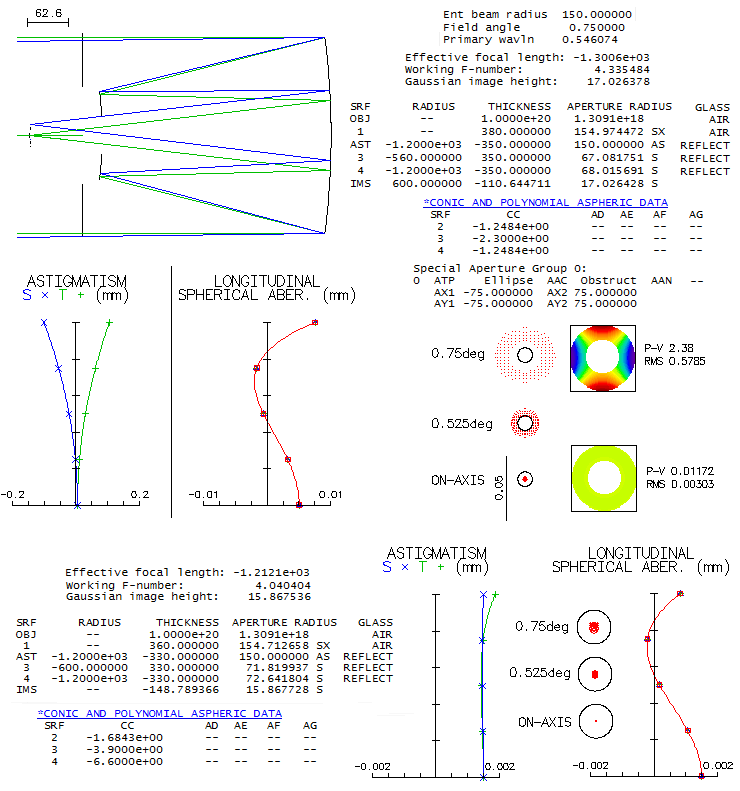
be made small as desired, at a price of reduced field size. Below is a 200mm f/3/6.75 system of that kind.
At a field angle of 0.25° the effective central obstruction diameter is 0.2D. With two interchangeable
secondaries it would be able to switch between narrow-field-negligible-obstruction and
wider-field-larger-obstruction mode. Configuration does not call for the primary hole, nor baffle tube.
Even more than the three-mirror system, cross-axis Gregorian is naturally
baffled from stray light by its very small diagonal mirror, acting as a tiny diaphragm placed near
the primary's focus. It does need some kind of support for the
diagonal which, considering its small size, can be a single stalk, or a circular vane spider.
Correction-wise it is same as a Gregorian with these mirror parameters. Since in this arrangement it's relatively
fast, aplanatic configuration is better a choice. That makes the mirrors two prolate ellipsoids. The effective
central obstruction is that of the diagonal in the cone converging from the tertiary (bottom left, with a
relation expressing the relative obstruction size). The diagonal may, and may not be offset; the effect on
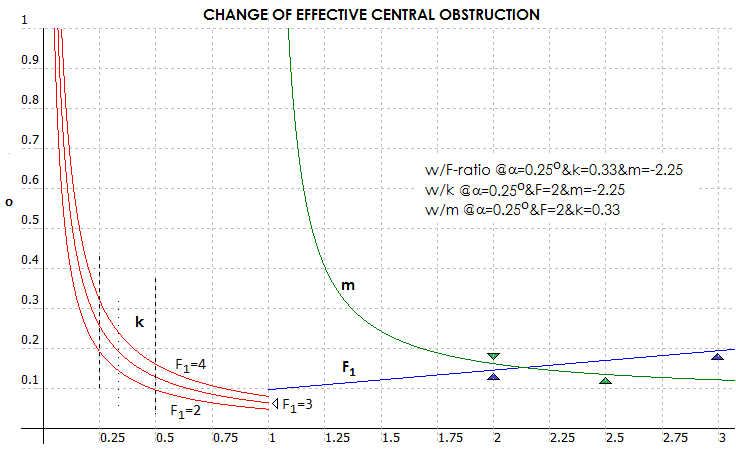
field illumination is small (bottom right). The three factors
affecting obstruction size are the primary mirror focal ratio (F1), relative size of the
tertiary
(k, the height of marginal ray on the tertiary in units of primary's diameter, i.e.
secondary-to-primary-focus in units of primary's focal length), and secondary magnification (m).
Graph below illustrates the corresponding change in obstruction size within their range.
Change in obstruction size is similar with a change in the primary focal ratio and secondary magnification. It is
significantly faster - all else equal - with a change in the relative secondary's size. For k~0.33 (0.25°
field angle and m=-2.25), central obstruction is below 0.15D with f/2 primary, less than 0.2D with f/3, and
less than 0.25D at f/4. At D~200mm linear field is still small, due to the relatively fast focal ratio, but
angular field is comparable to those of various tilted-element systems, generally significantly larger
for given aperture and
more awkward.
FIG. 127 illustrates degree of field correction of all-reflecting two-mirror telescopes
in their typical configurations, from classical Cassegrain and Gregorian,
through their aplanatic arrangements, to Dall-Kirkham, Schwarzschild/Couder
and Loveday.
|