|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
8.2.1. General aberrations
▐
8.2.4. Dall-Kirkham telescope
► 8.2.2. CLASSICAL TWO-MIRROR TELESCOPESWhile spherical aberration, according to Eq. 81, can be corrected for any appropriate combination of the primary and secondary mirror conic, the aberration coefficients for coma and astigmatism for two-mirror system show that coma and astigmatism do vary, potentially significantly, with the choice of conics. The coma aberration coefficient (Eq. 82) indicates that a system with spherical primary will have stronger coma than one with paraboloidal primary. A particular value of K1 resulting in the zero sum in the brackets, would result in corrected Seidel coma, with needed value for the secondary conic for corrected spherical aberration obtained from Eq. 80. In the early days of telescopes, limitations in both, calculation and mirror-making and testing skills would not allow to determine precisely the coma-free conic combination. However, it was determined that paraboloidal primary significantly reduces coma, compared to spherical (Eq. 82.1 shows that astigmatism with paraboloidal primary actually increases, but insignificantly in comparison with the reduction in coma). Thus, the choice for primary conic was, for quite some time, paraboloid and, for that reason, this arrangement is known as the classical two-mirror telescope. With paraboloidal primary (K1=-1), which is corrected for spherical aberration, zero system spherical aberration requires zero secondary spherical aberration, for which the needed secondary mirror conic is, from Eq. 80:
which makes it a hyperboloid. Since the requirement in the classical two-mirror system is that either mirror has zero spherical aberration, mirror conic can be alternatively determined from the fact that the object for each has to be located at one of its geometric foci. For the paraboloidal primary, the object is at its infinity focus. For the secondary, the object is the image formed by the primary, thus it has to coincide with secondary mirror's near geometric focus (at the far focus location, the final image wouldn't be real, that is, the rays would be diverging from the secondary). Equaling the near focus separation for the secondary given by R2/(1+ε2), ε2 being the surface eccentricity, with the secondary-to-primary's-image separation i (FIG. 121), requires secondary mirror eccentricity ε2=(R2/i)-1, or the secondary conic constant K2=-[(R2/i)-1]2 where, according to the sign convention, for the primary oriented to the left, both secondary mirror radius of curvature R2 and image separation i are negative in the Cassegrain and positive in the Gregorian. With the object at its near focus, secondary mirror will form the final image at its far focus, at a distance equal to R2/(1-ε2). After spherical aberration is corrected, remaining Seidel coma and astigmatism, as the P-V wavefront error at diffraction focus for object at infinity are given by:
respectively, with α being the field angle in radians, D the aperture diameter, F the system F-number and f the system focal length. The coma RMS wavefront error is related to the P-V error as: ω = Wc/32 = αD/272F2 = h/272F3 (84.3)and for astigmatism: ωa=Wa/241/2 (84.4)
Evidently, coma is identical to that of a paraboloid of the same F-number, while the astigmatism exceeds that of a paraboloid by a factor (m2+η)/(1+η)m. Sign of astigmatism in the Gregorian and Cassegrain is identical (both. m and f are numerically negative in the Gregorian, while positive in the Cassegrain). Therefore, related geometric (ray) aberrations can be determined from those given for a paraboloid in 2.2. Coma and 2.3 Astigmatism. From Eq. 84.1-84.4, the coma-to-astigmatism RMS wavefront error ratio in a classical Cassegrain is closely approximated by D/5.5mh. This implies that, for given linear height in image space, the relative astigmatism increases with secondary magnification. For given angular height, it increases with the square of secondary magnification. Petzval field curvature of any two-mirror system is given by 1/Rp=2[(1/R2)-(1/R1)], R1 and R2 being the radius of curvature of primary and secondary mirror, respectively. However, due to the presence of astigmatism, best image surface curvature varies. With the primary mirror astigmatism independent of the conic (for the stop at the surface), it is the secondary mirror conic and shape (convex/concave) that induces variations in the system astigmatism. For classical two-mirror systems, median field curvature is given by:
The relation shows that, for given primary f-ratio and
secondary magnification, best (median) image surface is somewhat less
curved in the Gregorian (see
graph). This is despite its considerably stronger Petzval surface curvature, due to its astigmatism, opposite in sign to
its Petzval, resulting in the astigmatic surfaces forming on the convex
side of the Petzval, thus less curved relative to it. In the Cassegrain,
astigmatic surfaces form on the concave side of its Petzval surface,
with their curvatures consequently stronger (note that Petzval surface
is concave toward secondary in the Cassegrain, and convex in the
Gregorian).
Alternatively, secondary conic can be found from
K2=-[(R2/i2)-1]2
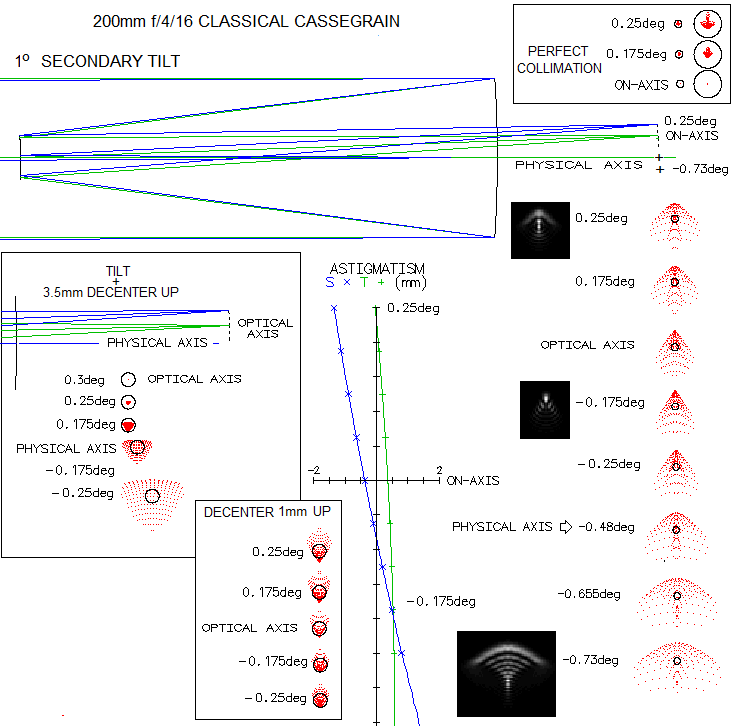
which, for the secondary mirror radius The wavefront error of coma is identical to that of a 300mm f/16 paraboloid; at 0.25° (21mm, 0.00436 radians) off-axis, it is Wc=αD/48F2=0.0001065, or 0.194 wave P-V in units of 550nm wavelength. The RMS wavefront error of coma is smaller by a factor of 1/√32, or 0.034 wave. At the same distance off-axis, astigmatism is Wa=-(m2+h)Dα2/8(1+h)mF=0.00015mm, or 0.27 wave P-V in units of 550nm wavelength; the corresponding RMS wavefront error is 0.056. With R1=-2400mm and R2=ρR1=mkR1/(m-1)=0.32R1=-768mm, the Petzval curvature is Rp=-565mm, and the best (median) field curvature is Rm=-315mm. Above applies to a perfectly collimated system. Less than perfectly aligned mirrors will induce additional aberrations, axial and abaxial. Taking the above system, effect of secondary tilt and/or decenter is illustrated below.
The effect of 1° secondary tilt (about 0.5mm tilt at the edge, counterclockwise, top and right) is very obvious. Part of it is the consequence of the axial ray bouncing far off the physical field center - as the raytracing scheme shows - bringing into the physical center uncorrected portions of field. Also, tilt of the secondary vs. converging beam creates at its surface all-field coma, i.e. coma of even magnitude imposed over entire field. Here, tilting the secondary 1° counterclockwise throws the optical axis - and optical field center - nearly 0.5° off the physical system ais, i.e. physical field center. Near optical field center the aberration is nearly eclusively the all-field coma, while astigmatism creeps in going farther off. As the astigmatism plots shows, image field is also tilted, which is of little significance considering the magnitude of field aberrations. Even this much of misalignment can be nearly cancelled out by inducing offsetting misalignment - in this case 3.5mm decenter (left, above). However, the cancelling takes place at the optical axis, which is still 0.3° off the physical axis, i.e. physical field center. Decenter of 1mm alone induces all field coma, with the physical field center located about 0.06° above the optical axis. In general, magnitude of aberration induced by element tilt/decenter is in proportion to the numerical deviation from perfect. Change in the mirror spacing induces spherical aberration. Every mm of spacing reduction extends back focus by little over 15mm, inducing about 0.014 wave P-V of undercorrection.
|