4.3. Telescope astigmatism

Similarly to coma, astigmatism is an off-axis point wavefront aberration, caused by the inclination of incident wavefronts relative to the optical surface. However, while coma always originates at the optical surface, astigmatism, in its simplest form, for mirror with the stop at the surface, results simply from the projectional asymmetry arising from wavefront's inclination to the surface. The diameter of wavefront's projection onto the surface varies from the minimum in the plane of wavefront tilt - determined by the chief (central) ray and optical axis (which also defines the tangential plane) - to the maximum in the direction orthogonal to it (sagittal plane), where it equals aperture diameter.

Since the focal length (i.e. radius of curvature of the wavefront) changes with the square of the diameter for given sagitta depth, the two orthogonal wavefront sections focus at the longitudinal separation of (1-cos2α)ƒi, which constitutes longitudinal astigmatism (α is the field angle in degrees, and ƒi is the image-to-pupil separation, equal to focal length for distant objects). This applies to lens with the stop at the surface as well.

Another peculiarity of astigmatism is that a cross-section along any wavefront diameter is still spherical, but with the radius of curvature varying with the pupil angle. Thus the wavefront form as a whole deviates from spherical.

For displaced stop - either first optical surface significantly separated from the aperture stop, or secondary and tertiary surfaces (whose stop is formed by a preceding surface) - other surface properties, such as shape, position and conic, also can influence the size of astigmatism. This is due to the displaced stop for these surfaces changing the surface radial asymmetry profile. FIG. 43 illustrates the form of astigmatic wavefront deformation for primary astigmatism, and the resulting geometric (ray) aberration.

FIGURE 43: RIGHT: Primary astigmatism on mirror surface, as a result of the projected diameter of the incoming wavefront (Wi) varying with the radial orientation. For the inclination angle shown, the width of vertical, or tangential (with the tangential plane determined by the axis and chief ray) wavefront projection onto the surface, given by cosαD, is at its minimum, gradually increasing with the radial angle around the chief ray to the maximum projection width D in the orthogonal (horizontal, or sagittal) orientation. With the wavefront sagitta (depth) constant, its radius (the focal length) varies with the square of diameter. Being of the smallest diameter, the wavefront section Wt in the tangential (vertical) plane focuses closest, and the wavefront section Ws in the sagittal plane farthest away from the mirror. LEFT: An illustration of the actual wavefront deviation from the corresponding reference sphere (red dots): for the reference sphere WP centered at the mid point of defocus M, and for the two reference spheres centered at either sagittal or tangential focus (S and T, respectively; the deviation for the former has cylindrical form oriented horizontally, for the latter vertically). The P-V error is identical at all three focus location; however, the deviation averaged over the wavefront is lower at the mid-focus by a factor 0.82, making it best (diffraction) focus. Solid blue line in best focus wavefront deviation (M) represents the deviation along the central cross-section of the actual wavefront vs. perfect reference sphere centered at the mid-focus point. The dashed blue line is a projection of the deviation along the wavefront edge, indicating saddle-like shape of the wavefront deformation.

Gaussian focus for astigmatic wavefront lies on the Petzval surface of an optical surface, or a system. Balancing defocus aberration for this point - located on the opposite direction from the sagittal focus, and at identical distance from it as the best focus - is zero, and the wavefront error is largest. Between the sagittal and tangential focus, ray disturbance resulting from the astigmatic wavefront deformation takes on rather peculiar form (FIG. 44).

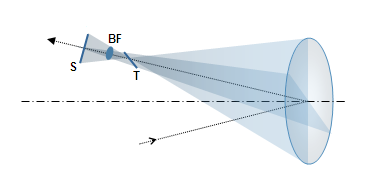
FIGURE 44: Geometry of the astigmatic defocus produced by a mirror with the stop at the surface: the wavefront radius at the pupil gradually increases from the minimum in the tangential (vertical) plane to the maximum in the orthogonal to it sagittal plane. Consequently, all wavefront meridians focus at a different length, producing longitudinal defocus, as an axial separation between tangential and sagittal focus. At the sagittal plane focus S it forms sagittal line, contained in the tangential plane. And at the tangential plane focus T it forms tangential line, laying in the sagittal plane. The lines transform into ellipses of decreasing eccentricity toward the inside of defocus zone. Midway between the two lines is the circle of least confusion (BF), which is the location of best astigmatic focus.

Aberration function for primary astigmatism given in Table 4 is for tangential focus, which is identical to that for the sagittal focus, except for the orientation. Neither coincides with the best (diffraction) focus, which is located midway between the two, hence requires correction by defocus. Since for given longitudinal aberration the P-V wavefront error for primary astigmatism equals that for defocus, the defocus added to it is equals half the P-V wavefront error of astigmatism. Aberration function for the wavefront error of primary (lower-order) astigmatism at best focus is given by:

Wa = Aρ2(cos2θ - 0.5) (18)

with A being the astigmatism peak aberration coefficient, ρ the normalized (to 1) height in the pupil, and θ the pupil angle. It shows that the wavefront error peaks for ρ=1 and cos2θ=1 and 0 (that is, for θ=0, π/2, π, 3π/2 and 2π), which is, every 90 degrees (with the successive peaks being of opposite sign), and orthogonally to the orientations of the minimum wavefront deviation, occurring for cosθ=√0.5 (for θ=π/4, 3π/4, 5π/4 and 7π/4). It clearly outlines saddle-shaped wavefront deviation, as illustrated on FIG. 43 left.

Note that the maximum wavefront error given by Eq. 18 - which gives ± wavefront deviations, not the peak-to-valley error - is one half of the peak aberration coefficient, which equals the P-V error. Numerically, it is identical to the P-V error at either sagittal or tangential focus, Wa=Aρ2cos2θ, but its RMS value is smaller by a factor of 1/√1.5.

When the point of maximum deviation in tangential (vertical) plane is closer to the center of reference sphere than its perfect reference point, the wavefront error of astigmatism is negative. That is the sign of astigmatism in a concave mirror, illustrated on FIG. 28. There is no difference in appearance between positive and negative Seidel astigmatism, since the pattern is merely rotated by 90°, and has an inherent 180-degree rotational symmetry at best focus location (FIG. 30).

The peak aberration coefficient A, which equals the peak-to-valley wavefront error, is given by:

A= aα2d2 = ah2/4F2 (18.1)

with a being the astigmatism aberration coefficient (simplified notation for 2w22 in Table 4), h the point height in image plane, α the field angle in radians (with α=h/ƒ for object at infinity, ƒ being the focal length) and d the pupil (aperture) radius. The aberration coefficient a for a concave mirror and stop at the surface is given by:

aM = n/R (18.2)

with R being the mirror radius of curvature. For mirror in air oriented to the left, n=1 and the aberration coefficient is aM=1/R. The sign of aberration coefficient indicates the tangential wavefront radius shorter than sagittal, and the sagittal line farther away from the mirror, as shown on FIG. 43-44. Positive astigmatism has this order reversed. From another perspective, the astigmatism wavefront error is negative when the optical path difference from the point of peak deviation in the tangential plane is smaller than the radius of a perfect reference sphere (the one centered at the mid point between tangential and sagittal focus).

So, the direct relation for the P-V wavefront error of primary astigmatism for concave mirror can be written as:

Wa = α2d2/R = α2D/8F = h2/8fF2 (18.3)

Shift to the best focus location is half the longitudinal aberration from either of the two line foci. In terms of the peak aberration coefficient A, needed wavefront error of defocus from either tangential or sagittal focus to best focus location is ±(A/2). While the P-V error remains unchanged for all three focus locations - sagittal, tangential and midway between these two - the latter has the RMS wavefront error smaller by a factor of 2/√6. As a result, this focus location has has the highest peak diffraction intensity, making it the best focus location.

The best focus RMS wavefront error in terms of the peak aberration coefficient - or P-V wavefront error - is given by:

ωa = A/241/2 (19)

Thus the P-V wavefront error of astigmatism corresponding to the diffraction limited RMS of ω=1/1801/2 is Wa=(24/180)1/2=0.365, in units of the wavelength.

Form of the aberration coefficient shows that the astigmatism wavefront error, unlike coma and spherical aberration, doesn't change with object distance. This is expected consequence of astigmatism of a mirror - as well as that of a lens (contact) objective - being a result of the asymmetry of wavefront projection onto the surface, rather than a product of the wavefront/surface interaction.

Astigmatism ray aberrations can also be expressed in terms of the peak aberration coefficient A as:

L = 8AF2, T = 4FA and Ta = 4A/D (20)

for the longitudinal, transverse and angular astigmatism, respectively (the last two as the circle of least confusion diameter). After substituting for A and mirror aberration coefficient a, the mirror transverse aberration - as the circle of least confusion diameter - can be also expressed as T= -Dα2/2 = -h2/2DF2 for object at infinity, with h being the point height in the image plane (note that aperture D needs to be in the metric used for the coefficient calculation, which also becomes the metric of transverse aberration). Since focal lengths of the astigmatic wavefront do not change with the height in the pupil (i.e. the zonal height), transverse astigmatism changes in proportion to the normalized pupil ray height ρ. With h=αƒ, ƒ being the focal length, angular astigmatism Ta=T/ƒ=α2/2F, where F is the focal ratio number F=ƒ/D. Longitudinal astigmatism L=-ƒα2.

There are simple geometric relationships between the circle of least confusion diameter and the sagittal and tangential line length, as well as between the three and the longitudinal aberration. The line length is double the circle diameter, and the longitudinal aberration is numerically greater than either line by a factor of F (the focal ratio), as illustrated in FIG. 44.

The transverse aberration in terms of the RMS wavefront error is Ta= ω√384/2.44, and in terms of the peak-to-valley error Ta=4A/2.44 (for ω and A in units of the wavelength), both expressed in units of the Airy disc diameter. That makes the astigmatic geometric blur significantly smaller for given amount of wavefront aberration than geometric blur for either spherical aberration or coma (FIG. 45). It is a stark remainder that optical criteria can

FIGURE 45: The ray spot size (top) and actual diffraction patterns for 0.37 wave P-V wavefront error of primary astigmatism (resulting in 0.80 Strehl, thus comparable to 1/4 wave P-V of primary spherical aberration). Perfect diffraction pattern is to the left. Geometric blur diameter at the best focus location (balanced primary astigmatism) is only 0.6 Airy disc diameters. There is no rays outside the Airy disc, yet considerable amount of energy has spread out from the spurious disc - result of the complex wave interference around best focus point (not unexpected, considering that rays focused to a point still produce a pattern). Compared to spherical aberration and coma, the energy spread is concentrated closer to the disc.

not be reduced to geometrical considerations; it is the underlying realm of electromagnetic field that determines the properties of the point object image.

As expected due to its uniformly dense geometric blur, the smallest RMS blur radius for astigmatism is at the location of the circle of least confusion. It is given by rRMS=FA√2, or smaller by a factor of √0.5 than the radius of the circle of least confusion. In units of the Airy disc diameter, the RMS blur diameter is RRMS=A√2/1.22, for the peak aberration coefficient A in units of the wavelength.

In terms of the RMS wavefront error of astigmatism ωa, the RMS blur diameter in units of Airy disc diameter is RRMS=4√3ωa/1.22.

EXAMPLE: A 200mm ƒ/5 concave mirror, d=100, R=-2000, F=5. Setting θ=0 and ρ=1, the peak wavefront error at h=1.4mm off-axis, giving the field angle α=1.4/1000=0.0014, is W=A/2=α2d2/2R=-0.0000049mm. The P-V wavefront error is twice greater - equal to the peak aberration coefficient - or -0.0000098mm. In units of 550nm (0.00055mm) wavelength, it is 0.0178, or 1/56 wave. Consequently, the RMS wavefront error ω=A/√24=0.000002mm or, in units of 550nm wavelength, 1/275 wave. The transverse astigmatism (circle of least confusion diameter) is T=4FA=20α2d2/R= =0.000196mm, or 0.03 Airy disc diameters, and angular astigmatism Ta=T/ƒ is 0.000000196 radians, or 206.265x0.000000196=0.04 arc seconds.

Since both, wavefront error and geometric (ray) aberrations are directly proportional to the aberration coefficient, it implies that they are in a constant proportion themselves. In other words, doubling the wavefront error also doubles the geometric aberration.

The RMS blur radius rRMS=FA√2=0.0000098mm, and the RMS blur diameter in units of the Airy disc diameter is RRMS=A√2/1.22=0.0207, for A in units of the wavelength.

Aberration coefficient of astigmatism doesn't change with object distance. For relatively close objects, transverse astigmatism increases as ƒi/ƒ, ƒi being the image-to-pupil separation. However, it doesn't affect the wavefront error: since the wavefront radius is also longer by the same ratio, identical nominal wavefront error results in proportionally greater longitudinal and transverse aberration.

For the aperture stop displaced from mirror surface, the aberration coefficient of astigmatism changes in proportion to Kσ2+(1-σ)2, with σ being the mirror-to-stop separation (positive in sign) in units of the mirror radius of curvature. The astigmatism aberration coefficient is:

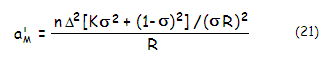
Needed stop separation for zero astigmatism is given by σ=[1-√|K|]/(K+1). Thus, astigmatism is canceled for σ=0.5 with a paraboloid and σ=1 with a sphere. The relation is not defined for K=-1 (parabola), but implicates σ=0.5 limit for K approaching -1. For positive values of the conic K, the aberration coefficient cannot be zero regardless of the stop position, since both Kσ2 and (1-σ)2 are positive.

Unlike coma, change in astigmatism caused by displaced aperture stop is independent of object distance.

Aberration coefficient of primary astigmatism for a lens with the aperture stop at the surface is identical to the one given for concave mirror (Eq. 19.1), with the radius of curvature R replaced by 2ƒ (Eq. 99), ƒ being the lens' focal length. For a contact doublet, it gives the peak aberration coefficient as a sum of the aberration coefficients at the first and second lens, respectively, as:

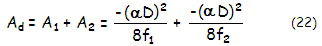
with α being the field angle, and ƒ1,ƒ2 the respective lens focal lengths (keep in mind that focal length of a negative lens is numerically negative in the left-to-right Cartesian coordinate system). Change of the stop position results in change of the aberration coefficient only with systems not corrected for spherical aberration, or coma, or both. Since modern refractor objectives commonly are aplanats, their astigmatism is not affected by the stop position. As already mentioned, wavefront error of astigmatism of the contact doublet doesn't change with object distance.

Strongly curved surface give rise to higher order aberrations, and astigmatism is no exception. Although relatively rare in amateur telescopes, secondary (higher-order) astigmatism can be significant in systems with sub-aperture correctors, as well as in some eyepieces. Unlike the P-V wavefront error of primary astigmatism, which is at either sagittal or tangential focus described with quadratic function (parabola, blue plot on FIG. 46 left), that of secondary astigmatism, given as Wa=Aρ4cos2θ, is quartic (4th power) function with a single turning point (red plot on FIG. 46 left). The shape of wavefront deviation is generally similar to that of primary astigmatism, but its near-cylindrical form has larger near-flat middle area and more strongly curved edges. The wavefront shape implies that secondary astigmatism forms longer sagittal/tangential focus lines when unbalanced, or balanced with defocus.

FIGURE 46: The form of wavefront deviation of secondary (higher-order) astigmatism (red) vs. that of primary astigmatism (blue). For given P-V wavefront error, the secondary astigmatism deviation, in its pure form (left), is flatter for central zones, and steeper toward the edges. Balanced with defocus alone, it takes a form similar to balanced primary astigmatism (shaded gray), only the saddle is flatter. It is minimized when balanced w/primary astigmatism

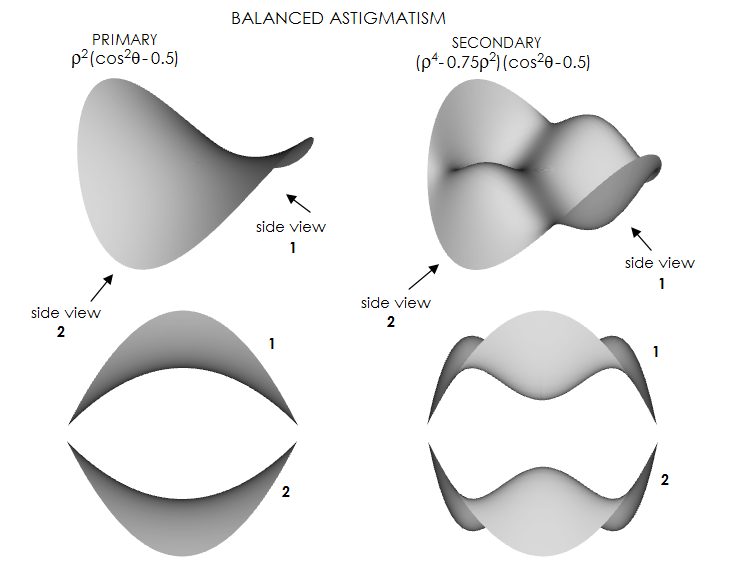
Similarly to that of the primary, the error of secondary astigmatism at either sagittal or tangential focus (left; tangential focus has the same shape simply rotated by 90° about vertex) is reduced by refocusing to the best focus midway between them (right). In either case, the P-V error remains the same, but the RMS error is reduced, and smaller for given P-V error for secondary astigmatism at both focus location.

The more efficient way of minimizing secondary astigmatism is, however, balancing it with the lower-order form of opposite sign. The error is minimized with adding the primary astigmatism with the peak coefficient smaller by 25%, with Was=A(ρ4-0.75ρ2)cos2θ, implying that the P-V error of of secondary astigmatism balanced with the lower-order form is smaller by a factor of 0.25 (fourfold) than at either sagittal or tangential focus. The RMS error is smaller than that of balanced primary astigmatism of identical P-V error by a factor √0.6.

However, due to the different rates of aberration increase for the two astigmatism forms (2nd vs. 4th power of field angle for the primary and secondary form, respectively) this optimized balancing is only possible at a narrow field zone. Usually, primary astigmatism is left to be larger initially, with the two forms balancing farther off axis and secondary astigmatism quickly becoming dominant after that.

◄ 4.2. Coma ▐ 4.4.Defocus ►

Home | Comments