|
telescopeѲptics.net ▪ ▪ ▪ ▪ ▪▪▪▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ CONTENTS
4.4. DEFOCUS ABERRATION
PAGE HIGHLIGHTS Formally, defocus wavefront aberration results from the image formed by a telescope objective being observed not at the location of the Gaussian image point, but at a point longitudinally displaced from it. In more practical sense, defocus error occurs when point of observation is displaced from best, or diffraction focus, a point with peak diffraction intensity embedded into longitudinal extension of the central maxima. Longitudinal shift away from this point, to either side, results in gradual decrease of central intensity, with the energy spreading from the central maxima out to the rings area. In its pure form, defocus occurs in aberration-free aperture, in which case the longitudinal defocus error equals longitudinal displacement from Gaussian image point, and the corresponding P-V wavefront error is given by the sagitta difference between two reference spheres in the entrance pupil: one centered at Gaussian focus (F on the illustration below), and the other at the point of observation (Fd). Hence, longitudinal defocus is given by the difference between the two radii, Ld=R-Rd, where R is the pupil-to-image distance (equaling focal length for object at infinity) and Rd the distance from pupil to the point of defocus. The corresponding P-V wavefront error equals the differential between two sphere's sagitta, given with the expansion series Wd=[(1/Rd)-(1/R)]D2/8 + [(1/Rd3)-(1/R3)]D4/32 + ... = ΔD2/8RRd + Δ(R3+Rd3)D4/32R3Rd3 + ..., where Δ is the longitudinal defocus (thus Rd=R+Δ). Since the second term already is smaller than the first term by a factor ~3ΔD2/4R2~3Δ/4F2, a full aperture P-V defocus wavefront error, for Δ values of ~λ (wavelength unit) and smaller is accurately (within a small fraction of percentage point) given by: Wd
= [(1/Rd)-(1/R)]D2/8
= ΔD2/8RRd
= Δd2/2RRd (23)
with D being the aperture diameter. The error sign is positive
when the OPD from the aberrated to focal point is larger than that from
the point at identical zonal height at the reference sphere, and
negative for smaller OPD (on the illustration bellow, the wavefront
error is numerically negative).
Figure bellow shows the diagram of defocus error (top), as well as the
changes in the appearance of otherwise aberration-free diffraction
pattern for unobstructed aperture caused by increasing defocus error
(bottom) and change in the longitudinal peak intensity as a result of
defocus .
In such instances when this is not the case -
such as the presence of spherical aberration, or astigmatism - certain
amount of defocus from the Gaussian image point is necessary to shift to
the actual best focus location. In other words, defocus can be balanced
with another aberration in order to have the combined aberration
minimized (for instance, best focus in the presence of
spherical
aberration is at the point halfway between paraxial and marginal focus,
thus combines spherical aberration and defocus). In everyday's
jargon, "defocus" has somewhat different meaning: it is simply an
axial deviation from best focus location, correctable by mere
refocusing.
Back to best focus being coinciding
with the Gaussian, defocus P-V wavefront error
is measured as the optical path difference between a perfect reference sphere for the
point other than the Gaussian, and a perfect reference sphere
for Gaussian image point. It is
expressed as:
Wd = Pρ2
(24) with
ρ
being the in-pupil ray height in units of pupil radius, and P
the peak aberration coefficient for defocus (equal to the P-V wavefront
error) given by Eq. 23.
It changes with the square of pupil height.
For very small relative difference between
the two reference radii, such as those for typical defocus values in
telescopes,
Eq. 24 can be written as
Wd
~ (Rd-R)D2/8R2
~
ΔD2/8R2 (24.1).
with
Δ
being the longitudinal defocus (effectively, the difference in radii
between the two reference spheres). Since this approximation differs from the exact value by a factor of Rd/R,
it is as good as the exact value for all practical purposes (for
instance, the relative difference between the true value and
approximation for 1mm defocus in a 200mm
f/10 system is 0.9995, and still
only 0.9975 in a 80mm
f/5 system).
With R
equaling the system focal length f for object at infinity, (D/R)2=1/F2,
where F is the system focal ratio f/D, and the peak aberration
coefficient for defocus, equaling the P-V wavefront error, is:
P = -Δ/8F2, (24.2)
It is radially symmetrical aberration, with
the geometric blur diameter given simply by
Bd=Δ/F.
Substituting for Δ from
Eq. 24.2, geometric defocus blur diameter in terms of the P-V
wavefront error is
Bd=8P,
in units of λF
(which implies P=0.305λ
for the blur equal to Airy disc diameter). In units of the Airy disc diameter (2.44λF) for
defocus is:
or Bd=745Δ/F2 for 550nm (0.00055mm) wavelength. Since the peak aberration coefficient P equals the P-V wavefront error Wd for ρ=1, the blur size in Airy disc diameters is, from Eq. 26, also given by Bd=8W'd/2.44, with W'd being the P-V wavefront error of defocus in units of the wavelength. Actual diffraction pattern, when defocused to a given W'd value (from about 0.5 up) is somewhat larger than indicated by Bd, due to the actual pattern always having certain depth, hence showing a portion of wider external energy spread away from the focal point.
The peak defocus aberration coefficient
- i.e. P-V wavefront error - and the
RMS wavefront error relate
as
ωd=P/√12=Wd/√12.
This implies that the P-V wavefront error of defocus corresponding to
"diffraction-limited" level, (i.e. to ω=1/√180,
for 0.80 Strehl) is P=√12/√180=1/√15=0.258,
in units of wavelength.
The RMS wavefront error
relates to blur diameter Bd as
ω=2.44Bd/√768.
The RMS blur spot radius for defocus, rRMS=PF√8.
The RMS spot diameter expressed in Airy disc
diameters, is
RRMS=Wd√8/1.22
in terms of the P-V wavefront error, and
RRMS=4√6ωd/1.22in
terms of defocus RMS error
ωd.
In terms of phase error, the peak value of defocus phase aberration is
given as Φd=πΔ/4λF2,
in units of the full phase of 2π
radians (thus giving the P-V wavefront error in units of wavelength when divided
by 2π).
The corresponding Strehl ratio is given by S=sinc2(Φd/2)=[sin(Φd/2)/(Φd/2)]2=[sin(180Δ/8λF2)/(πΔ/8λF2)]2.
The peak defocus phase aberration is Φd=1.43
radians, or 1/4.4 of the full phase of 2π.
The corresponding Strehl is S=0.84.
An important property of a telescope is its
defocus sensitivity. As
Eq. 24.2 implies, it is
proportional to the longitudinal defocus Δ, and inversely proportional
to F2.
Since P equals the P-V wavefront error Wd
of defocus, expressing it in units of the wavelength gives W/λ=-Δ/8λF2.
Hence taking the maximum allowable P-V wavefront error of defocus Wd/λ, in either direction from the exact focus, the
corresponding longitudinal range (including both
sides of defocus) within
which defocus error will not exceed this level is given by:
where W=Wd/λ
is the defocus P-V wavefront error in units of the wavelength. In terms
of the RMS wavefront error
ω,
Ld=32√3ωλF2.
It is sometimes called focus depth,
not to be confused with the meaning of the same term in photography and,
sometimes, ophthalmology. The latter has little to do with the actual
optical quality, merely indicating the range of geometric defocus within
which a circle of confusion (defined as vertical cross-section of an
assumed perfect converging/diverging cone) does not exceed certain size,
usually 0.2mm or 0.01 inch, when magnified to the usual 8x10
format, observed from the usual ~1 foot distance. That amounts to the
angular blur size of little over 2 arc minutes, at best referring to the
defocus magnitude in an imaginary perfect system.
Focus depth in telescopes is also not to be confused with
field depth, a photographic term referring to the range of distance
in object space within which object image retains needed quality
level; given, with respect to infinity focus, by Δ=±
8Wn
(o-f)2
/[D2-8(o-f
)Wn],
where o is the focused distance, larger than f for close objects,
f
and D the system focal length and aperture diameter,
respectively, and Wn
the nominal P-V wavefront error of
defocus, it is irrelevant in astronomy, where all objects are very
distant.
Taking W=0.258 for 1/3.87 wave of defocus (0.0745 wave RMS) allowable
for the conventional "diffraction-limited" level of 0.80
Strehl, gives the corresponding
± range of defocus as Ld=4.13λF2.
For an
f/10 system and λ=0.00055mm,
it gives 0.227mm.
This is, of course, an idealized system. In the presence of spherical
aberration - rather common scenario - allowed defocus is significantly
smaller. For a system with
the P-V wavefront error W of lower-order spherical aberration in
units of the wavelength - assuming W<0.25 for better
than "diffraction-limited" level - with the corresponding longitudinal
aberration LAs=64λWF2, allowed
± defocus range for remaining at the
conventional "diffraction-limited" level, or better, is given by
Lds=xLAs,
with x=(1-16W2)0.5/4√15W
obtained from Eq. 6.
Hence diffraction-limited defocus range in the presence of spherical
aberration is given by:
Lds
= 16λ(1-16W2)0.5F2/√15 (26.1)
Taking W=1/6, for λ/6 wave P-V of
spherical aberration, and λ=0.00055mm,
allowable defocus range in an
f/10 system (so F=10) is 0.169mm
(note that "defocus range" in this context doesn't equal defocus error;
at the best focus location, lower-order spherical aberration is already combined with
longitudinal defocus equaling one half of the longitudinal spherical
aberration).
For W=0.25, i.e. λ/4 wave of
lower-order spherical aberration in the system, allowed defocus to remain within "diffraction-limited" range
is zero. Eq. 26.1 is accurate for 0.25≥W≥0.0625; for W=1/16, the
diffraction limited defocus range becomes identical to that of
aberration-free aperture for
±λ/4 wave of defocus, as shown on the illustration to the left,
depicting error function over the range of longitudinal spherical
aberration, given with Eq. 6
(units on the horizontal axis are Λ,
longitudinal aberration normalized to 2 for λ/4
P-V error of spherical aberration; note that the P-V wavefront error of
defocus is slightly larger for given RMS error). For W<1/16, Eq. 26.1
gives slightly larger values for diffraction-limited defocus range, than
what is obtained for the λ/4 wavefront
error of defocus range. This is a consequence of the defocus RMS error
being, for given P-V wavefront error, slightly smaller - by a factor of (11.25/12)0.5
- than the RMS error of spherical aberration. For
zero wavefront error of spherical aberration (W=0), Eq. 26.1
gives diffraction-limited range larger by a factor of (12/11.25)0.5
than the range for λ/4 wave of defocus.
That is the true diffraction limited defocus range, for the RMS error
producing 0.80 Strehl at either end; the corresponding P-V wavefront error of defocus
is, as mentioned before, 0.258λ.
In aberration-free systems with central
obstruction, defocus RMS error is smaller by a factor of (1-o2)
than in unobstructed aberration-free system,
o being the relative c. obstruction size in units of the aperture
diameter. Consequently, the Strehl ratio in terms of peak defocus phase
aberration Φd,
for linear defocus Δ, is given by
S=sinc2(Φd(1-o2)/2)={sin[Φd(1-o2)/2]/[Φd(1-o2)/2]}2=
={sin[(180Δ/8λF2)(1-o2)]/(πΔ/8λF2)(1-o2)]2.
If spherical aberration is present, the RMS wavefront error of defocus is
reduced by a factor of (1-o2)2,
and its defocus error changes similarly to that in clear aperture with
spherical aberration. Hence, in terms of error added by
defocusing, obstructed system with spherical aberration has wider
defocus range than unobstructed system with identical level of spherical
aberration. However, its starting point - best focus quality level - is
degraded by the effect of obstruction. In order to have any
diffraction-limited defocus range, an obstructed aperture needs to have
normalized peak diffraction intensity greater than 0.80. This implies
the optics Strehl better than 0.8/(1-o2)2.
With even moderate linear obstruction ratio o=0.25 (i.e. 0.25D), a
system needs to have the optics Strehl better than 0.91 (i.e. better
than 1/6.1 wave P-V of spherical aberration level). A 0.95 optics Strehl
system, or slightly better than 1/8 wave of lower order spherical level,
cannot add more than about 1/24 wave of P-V wavefront error and remain
diffraction limited. Unobstructed system with identical correction error
can add three times as much of P-V wavefront error (1/8 wave),
implicating roughly three times wider diffraction-limited defocus range
for given relative aperture. |
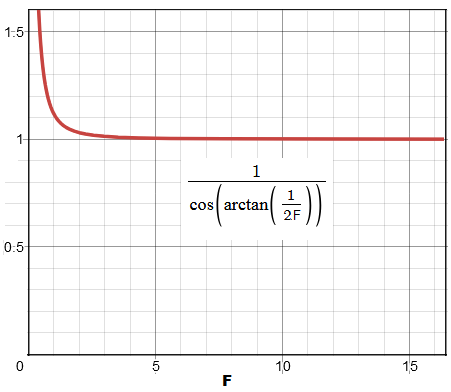Note that this simplified expression assumes the cosine factor of the marginal ray path to be 1, i.e. ray path parallel with the optical axis; the actual P-V error is larger by a factor of 1/cos[arctan(1/2F)], with the difference reaching 1% in an f/3.5 system (it is also not the actual value, since the two ray paths toward focus point have slightly different angles, but the difference is entirely negligible). As a graph at left shows, the difference is practically negligible for nearly all actual systems; even at f/1, when the difference between the simpler and more exact form for the P-V error exceeds 11%, the actual Strehl value for the "diffraction limited" level (0.80) given by the former would be 0.76.
FIGURE
48: Comparative plots for P-V wavefront error of defocus (red) and
selected levels of primary spherical aberration (blue). Unlike defocus
error alone (in a system with zero spherical aberration), which has
linear rate of change from or toward the minimum at the best focus location
(1 at the scale representing longitudinal spherical aberration
normalized to 2, i.e. 0<Λ<2),
spherical aberration causes the rate of
change to be slower around best focus location, while tending to
equalize with the defocus-alone-error farther away from it. Diffraction
limited defocus range for zero-spherical aberration is constant,
identical to the longitudinal spherical aberration range for λ/16 wave
P-V. In the presence of spherical aberration greater than λ/16 wave,
diffraction limited defocus range shrinks: subtly at λ/8 wave, but
quickly dropping to zero at λ/4 wave.