|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
10.2.2.4.1. SCT
off-axis aberrations
▐
10.2.2.5.
Schmidt-Cassegrain cameras
► 10.2.2.4.2. SCT focusing errors
PAGE HIGHLIGHTS Focusing error in a Schmidt-Cassegrain telescope results from deviations from the optimum mirror separation in order to: (1) shift focus location to accommodate use of accessories, or even different eyepieces or (2) keep focus location nearly fixed while focusing on close objects. Both are an issue with SCT systems that use mirror focusing - typical for a commercial SCT. For comparison, error induced while observing close object will be included for an SCT with conventional focusing (fixed mirrors) as well. Extending focus with object at infinity
Depending on the accessories used, required shift from the optimum focus can be more or less than that. Since moving the primary only changes the aberration contribution of the secondary, it is the error differential at the secondary determining the resulting system error. The resulting system error is, in effect, the despace error for two mirror system. For spherical secondary (K2=0) it is from Eq. 91.3 given as: W=(1-m2)∆/512m3F14 as the P-V wavefront error at the best focus, where m is the secondary magnification and F1 the primary focal ratio f/D. The relation implies that, for nominal primary mirror shift ∆, error induced by extending back focus is independent of aperture. It only depends on secondary magnification and primary's focal ratio. For F1=2, m=5, and K2=0, every mm of reduction in mirror separation (∆=1), or nearly for every inch of focus extension, induces ~1/23 wave P-V wavefront error of over-correction, and as much of under-correction for widening the separation. Aspherizing the secondary would result in the error of similar magnitude, only the sign of aberration would reverse: focus extension (i.e. reducing mirror separation) would induce under-correction. Focus extension also induces undercorrection to Celestron's Edge, about 1/20 wave P-V for every inch of extension. In addition, its off axis astigmatism nearly triples, transforming the field from practically flat into a very curved one (for 8-inch aperture, 190mm curvature radius, convex toward the secondary, with the flat-field wavefront error 0.5° off axis nearly four times larger). This level of error remains nearly unchanged with the change in aperture. This is due to any given mirror shift being producing identical nominal change of the height of marginal ray at the secondary. In other words, the relative ray height change is proportionally smaller for larger aperture. Since the aberration contribution of the secondary is in proportion to the fourth power of its effective aperture (Eq. 78.1), the relative change in its aberration contribution is approximated by 1+(4∆'/D), ∆' being the change in marginal ray height, ∆'=∆/2F1. Hence, the relative increase in secondary mirror contribution is proportionally smaller for larger aperture, but since its contribution is also proportionally greater, the final nominal change in its aberration contribution remains at the nearly same level. Spacing error also induces coma. For reduced mirror separation, it adds to the system coma, but not significantly (less than 10% for 5 inch focus extension). Close object focusing However, this only applies to the change in mirror separation to accommodate the use of various accessories, while the object of observing remains at a large distance. In addition to the change in mirror separation, focusing on relatively close objects has to deal with optical consequences of the change in shape of the incident wavefront (which is now convex spherical) as well. Follows more detailed consideration of how it affects performance level of a typical commercial SCT. Observing close terrestrial objects is not what telescopes are made for. Any optical system can give optimum performance only within a limited object distance range or, in terms of geometric properties of incident light, for a certain degree of curvature of the incident wavefront, determining geometry of rays projected from it. Telescopes are optimized for distant objects observing, hence for a near-flat incident wavefront, or bundles of near-collimated (parallel) rays. The smaller object distance, the more convex-spherical shape of the wavefront, and the more diverging the rays. This change in light geometry, without an adequate change in properties of the optical surfaces of telescope objective, results in the wavefront it forms being different from spherical - the closer object, the more so. In an SCT optimized for infinity, near-zero level of spherical aberration is achieved by balancing aberration contributions of its three optical elements, Schmidt corrector, primary and secondary mirror, for near-flat incoming wavefront. As the shape of the incident wavefront changes, so do the individual aberration contributions of these three elements. The problem is that they do not change in proportion that would preserve the near-zero balance. Instead, certain amount of aberration is generated, increasing exponentially with the reduction in object distance. Typically, the most significant aberration generated while observing close object with telescopes is spherical. The same applies to the SCT. Change in its off-axis aberrations is insignificant. Spherical incoming wavefront affects the three SCT optical components differently. Due to its low power, changes to the wavefront at the corrector are small enough to be neglected. Not so with the primary mirror. New wavefront/ray geometry result in larger effective mirror diameter and extension of its converging cone. These, in turn, increase the width of converging cone at the secondary, extending its converging cone significantly more. Most importantly, the aberration contributions to the wavefront at the primary and secondary change in different proportions, resulting in the aberrated final wavefront (FIG. 177).
In order to establish more specifically the amount of spherical aberration generated in an SCT used for close object observing, we need to track down changes in the aberration contribution for each of its three optical elements. While the change in contribution of the corrector and primary mirror is independent of the type of focusing, the aberration at the secondary mirror will be different in SCT systems that use mirror focusing (the common commercial type) from that generated by systems that use conventional focusing via focuser tube. If the two mirrors are stationary, the amount of aberration induced by close object observing is practically limited by the available focuser travel. Since closer objects are imaged farther back, at a certain point the image simply runs out of a focuser reach. The limit to object distance set by given focuser travel length can be approximated by treating the SCT as a two mirror system with the aperture stop at the corrector location. The effect of the corrector plate on ray geometry is minor, as described in 11.5. Schmidt-Cassegrain telescope. For given mirror separation s, back focus distance - the separation from mirror surface to the final focus - in a two-mirror system is given by B=s+(f1-s)f2/(f1-s-f2), with f1 f and f2 being the primary and secondary mirror focal length, respectively (note that, according to the sign convention, all three parameters are negative). With a close object, it is given by B=ρ'k'f1'/(ρ'-k'), with the ▪ new primary's effective aperture radius d'=(1-k)ψd/[1-(1-k)ψ] ▪ new (effective) primary's focal length f1'=f1/(1-ψ), ▪ new secondary-to-primary radius ratio ρ'=(1-ψ)ρ, ▪ new marginal ray height at the secondary k'=1-(1-ψ)(1-k)=(1-ψ)k+ψ, and ▪ primary focus extension ψf1/(1-ψ) with ρ and ρ' being the R2/R1 ratio for object at infinity and close object, respectively (with the secondary radius shrinking relative to the effective primary's radius), k and k' the relative secondary size vs. the effective primary diameter, also for infinity and close object, respectively, and f1 and f1' the primary's focus distance for object at infinity (focal length) and close object, respectively. For the typical commercial SCT configuration, with s~0.75f1 and (f/f1)~5, or ρ~0.3125 and k~0.25, the back focal distance is well approximated by B~0.23(0.33+ψ)f1/(0.06-ψ), with ψ=f1/O being the inverse object distance O in units of the primary's focal length. For an 8" f/10 SCT with f1~400mm, the focus shift between ψ=0 (object at infinity) and ψ=0.01 (object at 100f1, or 40m) is 0.3f1, or 120mm - most likely already out of the focuser range. For ψ~0.06, back focus distance approaches infinity (the secondary forms collimated beam of light), and for ψ>0.06 back focus distance has negative value (secondary forms diverging beam of light). To determine the level of spherical aberration induced to a commercial SCT at this and other object distances, it is necessary to determine the changes in aberration contributions of its three optical elements. For the typical commercial SCT configuration with spherical mirrors, the system wavefront error, as the P-V error of lower-order spherical aberration at the best focus, can be approximated from Eq. 113.2, by
with P, 1 and S being the proportional contributions of the corrector, primary and secondary mirror, respectively, and aperture diameter D in mm. The sum of contributions - under-correction by the primary, over-correction by the corrector and secondary - is near zero in the well corrected system. Relatively small deviation from perfect figure on any of the three optical elements can be cancelled out by matching deviations on other two elements, but it is probably as hard to achieve high correction level doing this as it is to produce three near-perfect matching surfaces. For an f/2/10 200mm system, a sum in the brackets of 0.011 would result in ~0.25 wave of spherical aberration, over-correction if positive, under-correction if negative. Follows simplified analysis of the change in these contributions for close objects. Its primary goal is to illustrate the mechanism of change, but it should also give useful quantitative approximation of the effect. As already mentioned, change at the corrector is negligible. Spherical aberration added to it due to close object distance is merely that of a plane parallel plate of the same thickness (Eq. 105.1). For the mirrors, close object distance itself is a factor that changes the aberration contribution - for the primary directly, and for the secondary by changing the separation between it and primary's image (which is the object for the secondary) - and the compounding factor is the change in the effective aperture of both, primary and secondary. At the primary, according to Eq. 9.1, the aberration contribution changes with (1-2ψ)2, with ψ being the inverse of the object distance O in units of primary's focal length f1, i.e. the inverse of the relative object distance o=O/f1, hence ψ=f1/O=1/o. Since the effective aperture of the primary, due to the displaced stop, changes in proportion to (1+2σψ), σ being the corrector-to-primary separation in units of the primary's radius of curvature, the combined change in its contribution due to these two factors is in proportion to (1-2ψ)2(1+2σψ)4. Unlike the primary, for which there is only that one single scenario, the change of aberration contribution at the secondary depends on the focusing modality: it is either with a standard focuser and fixed secondary, or focusing by moving the secondary. Fixed secondary With fixed secondary, the extension of primary's cone due to object distance reduction has two effects: one is the wider cone at the secondary, resulting in magnification increase, and the other is the change in the cone geometry, resulting in the primary's image forming farther away from the secondary. The cone width at the secondary due to focus extension alone (i.e. with fixed primary's aperture) changes in proportion to 1-ψ+ψ/k. However, since the marginal ray at the primary is higher by a factor of 1+[2σψ/(1-2σψ)] or, slightly rounded, 1+2σψ, the final height is proportional to [1-ψ+(ψ/k)](1+2σψ). The aberration contribution due to the change in its object (primary's image) distance, according to Eq. 78.1, is a function of the inverse of the relative image distance Ω, in units of secondary's radius of curvature, in proportion to (Ω-1)2. With the focus extension of the primary due to close object distance being ψ/(1-ψ) in units of primary's focal length, the change in Ω is proportional to (1-ψ)k/[(1-ψ)k+ψ], where k is the relative height of marginal ray at the secondary for object at infinity (and also the relative separation of primary's image from the secondary in units of primary's focal length). Thus, the secondary aberration contribution as a function of object distance is proportional to {(1-ψ)kΩ/[(1-ψ)k+ψ]-1}2, and its change vs. (Ω-1)2, with Ω~2.5 and k~0.25 for the typical f/2/10 commercial SCT, comes to [(1-3.66ψ)/(1+3ψ)]2. With the ratio of change in the effective secondary diameter (determined by the width of the axial cone at its surface) given by [1-ψ+{ψ/k)](1+2σψ), with k being the relative height of marginal ray at the secondary for object at infinity, its aberration contribution to the lower-order spherical aberration of the system is now changed in proportion to [(1-3.66ψ)/(1+3ψ)]2[(1+3ψ)(1+2σψ)]4, leading to [(1-3.66ψ)(1+3ψ)]2(1+2σψ)4, or (1-0.66ψ-11ψ2)2(1+2σψ)4. With σ~0.4 in the typical f/2/10 commercial SCT, it is (1-0.66ψ-11ψ2)2(1+0.8ψ)4. Alternately, since object distance is directly related to image magnification, so that (Ω-1)=(m+1)/m-1), the secondary contribution can be expressed in terms of secondary magnification m2. Starting with the general relation for secondary magnification in two-mirror systems, m2=ρ/ρ-k for object at infinity, and substituting for ρ' and k' in m2'=ρ'/(ρ'-k') for object at a relatively close distance, gives the change of (m2'+1)/(m2'-1) vs. (m2+1)/(m2-1) as [2ρ-k-ψ/(1-ψ)]k/[k+ψ/(1-ψ)](2ρ-k), with the secondary contribution changing with the square of it. With ρ~0.3125 and k~0.25 of the typical f/2/10 commercial SCT, it comes, again, to [(1-3.66ψ)/(1+3ψ)]2. Here too, change in the aberration contribution due to the magnification factor gets multiplied with the change in the secondary aperture factor to yield the combined change in the aberration contribution at the secondary, for the same final contribution ratio [(1-3.66ψ)(1+3ψ)]2(1+2σψ)4. With the effect of changes in D and F being accounted for within the brackets, the P-V error of lower-order spherical aberration at the best focus as a function of the object distance in an SCT with fixed mirrors (i.e. standard focuser) can be expressed as a lengthy but simple approximation:
with the aberration contributions from the corrector, primary and secondary mirrors given in green, blue and red, respectively. For ψ=0.01, or object at 100 primary mirror's focal lengths away, D=200mm, F1=2, σ=0.4R1 and k=0.25, it gives the error as W~(0.71-0.9915+0.2948)D/2048F13~0.000171mm, or 0.3 wave of over-correction in units of 550nm wavelength. This is slightly less from what OSLO gives for such a system (0.34 waves); the discrepancy of 10-15% persists for other values of ψ, mainly due to the OSLO system having slightly smaller σ value (0.375) and including a small higher-order aberration contribution, accounting for about 3% of the total aberration. Moving secondary In the SCT with mirror focusing, the mirror separation s is increased - usually by moving the primary - in order to lower secondary magnification back to its infinity level, and bring focus for close objects back to its infinity location. For this to occur, the effective decrease in the R2/R1 ratio due to the extended primary's cone has to be offset by a lower secondary magnification in order to produce the same final focus location. Since the secondary-to-final-focus distance is mkf1, with object at infinity, and m'k'f1' for close object (where f1' is the "acting" primary's focal length equaling the length of extended cone), the final focus will nearly coincide when m'k'f1' equals mkf1. This neglect small additional shift of the secondary forward needed to produce slightly higher magnification to compensate for the backward shift of the secondary (relative to primary) from its infinity location, which has insignificant effect. The needed ray height on the secondary for m'k'f1'=mkf1 is k"=(1-ψ), which in turn determines secondary magnification at that location as m2"=ρ'/(ρ'-k") which, with ρ'=(1-ψ)ρ, gives m2"=ρ/(ρ-k). In other words, m2"=m2, with secondary magnification nominally unchanged vs. that with object at infinity. The ray height at the secondary is also nearly unchanged, since the slightly lower nominal k value is mainly offset by the slightly larger effective aperture of the primary. The actual ray height is slightly less than for object at infinity, but it is small enough to be neglected, more so considering that the secondary does need to be moved slightly forward in order to compensate for its shift away from the primary and reach the same final focus location. So, we can assume that the secondary mirror contribution is nearly the same as for object at infinity. The change in primary's contribution is the same as with fixed mirror, and there is no appreciable change in the corrector's contribution. Thus the P-V error of lower-order spherical aberration at the best focus induced by reduced object distance O/f1=1/ψ in an SCT with mirror focusing is:
For the same object distance O of 100 primary's focal length (ψ=0.01), the error for the above system is now W~0.18 wave of over-correction, practically identical to the 0.18 wave P-V error given by OSLO. That is 40% smaller error than with fixed mirrors. Since the error is, as in the fixed mirror system, nearly entirely lower-order spherical, the corresponding RMS wavefront error is smaller by a factor of ~0.3. Thus, correction error induced by close focusing is considerably smaller in SCT systems with mirror focusing (FIG. 178).
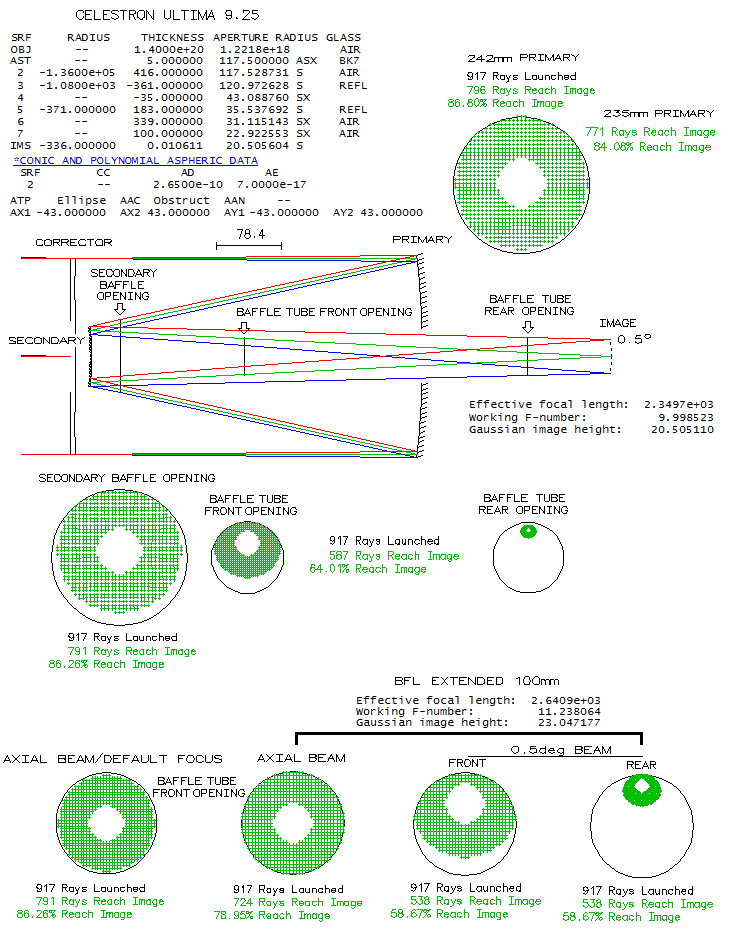
Simple empirical formulas roughly approximating close focusing P-V wavefront error in units of 550nm wavelength for mirror focusing and fixed mirror SCT systems are: W~D/1.8oF13 and W~D/oF13 (120.3) respectively, with o being the object distance in units of the primary mirror focal length (o=O/f1=1/ψ). For the typical commercial f/10 SCT, spherical mirrors and F1~2, the P-V error of spherical aberration induced by mirror focusing at close objects is approximated by W~D/72o', with o' being the object distance in units of system's focal length (as before, aperture diameter D is in mm). Significantly larger error induced by close object observing puts conventional (fixed mirror) focusing SCT at a definite disadvantage for close objects observing. More so considering the extent of axial image shift, which could make this type of observing either difficult, or impossible. SCT baffle system and extended focus One of the conveniences of the SCT is the ability of focus extension, in order to accommodate use of various accessories. This, however, may have two negative effects: (1) increased vignetting of the outer field, and (2) stopping down effective aperture. Both are the consequence of the tightly fit SCT baffles. Extending SCT back focus by moving the primary closer to the secondary places somewhat wider converging cone at the secondary baffle; with the cone converging from the secondary being also extended, the relative widening of converging cone is even more pronounced at the front and rear opening of the baffle tube. At the front opening, it can result in effectively reduced aperture. Also, since angles of divergence toward off axis field points are larger for the cone converging from the secondary (due to secondary's magnification), vignetting at off axis field points is more pronounced at the baffle tube openings. Scheme below is OSLO analysis of the consequences of focus extension in a Celestron C9.25 unit, starting with baffle-caused vignetting for the default focus location.
Specs for the baffle system are entered
according to actual measurements, since they are not supplied by the
manufacturer. At f/10, focus location is nearly 230mm behind the primary
(back focus), and about 100mm from the rear end of the baffle tube.
For this focus location, converging cone tightly clears the
front baffle tube opening, and the only significant vignetting within
0.5° field radius is for points close to field edge. Since the
converging cone width at the front tube opening is nearly identical to
the opening diameter, point illumination is given by I=(β/90)-c(sinβ)/π,
with cosβ=c/2, where c is the relative overlap of the converging
cone in units of the cone radius, and β is in degrees
(for graphing purposes it can be written as:
With the focus extended by 100mm from its f/10
location, the corresponding focal length is 2641mm. Converging cone at
the front baffle tube opening is is wider than the opening, resulting in
the aperture effectively reduced by less than 5% linearly, to ~225mm. Hence, the
effective focal ratio is now f/11.75.
More details on SCT field illumination are given on the example of
8-inch SCT. ◄ 10.2.2.4.1. SCT off-axis aberrations ▐ 10.2.2.5. Schmidt-Cassegrain cameras ►
|
 Strictly talking, commercial
SCT using primary mirror focusing
are misaligned every time the two mirrors are not at a single
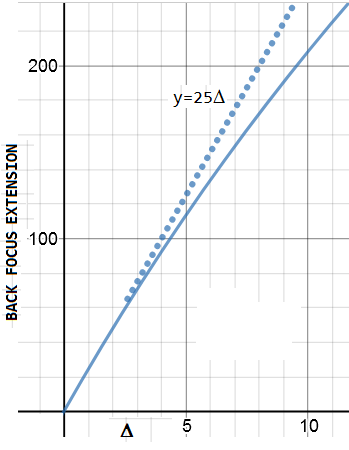
optimum separation. It is interesting to determine how it affects wavefront quality. For any change ∆ in the mirror separation, the final focus shifts axially by
-∆m
Strictly talking, commercial
SCT using primary mirror focusing
are misaligned every time the two mirrors are not at a single
optimum separation. It is interesting to determine how it affects wavefront quality. For any change ∆ in the mirror separation, the final focus shifts axially by
-∆m