|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
10.2.2. Schmidt camera
▐
10.2.2.2. Wright, Baker camera, Hyperstar
► 10.2.2.1. Schmidt camera: aberrations
PAGE HIGHLIGHTS The starting shape for the Schmidt corrector is plane-parallel plate. Seidel aberrations at the front surface of plane-parallel plate (for the wavefront formed inside the glass), as the aggregate P-V wavefront error at the best focus location, are given with:
with n being the refractive index, d the beam semi-diameter at the plate, h=αL the object height, with α being the field angle in radians, and I1 the first surface image distance, given by I1=nL, L being the object distance. Terms in the main bracket are for spherical aberration, coma, astigmatism, field curvature and distortion, respectively. The wavefront error for each aberration is obtained by multiplying the inside term with the outside (index) factor. Note that the pupil angle θ is dropped out by setting it to zero for all off-axis aberrations, which means that coma and astigmatism P-V wavefront error are those measured along the axis of aberration; that gives the peak P-V error value for both. Note that best foci for different aberrations do not necessarily coincide, so the error given by Eq. 105 is hypothetical. The actual aggregate error can be summed up at the Gaussian focus, where the first two aberrations are larger by a factor of 4 and 3, respectively. Evidently, all aberrations are zero for the object distance approaching infinity (i.e. for near collimated incident light). They are also entirely negligible for any terrestrial object that can be observed with a telescope featuring conventional focusing mechanism; for telescopes with mirror focusing, such is the common SCT commercial variety, the aberrations induced by the front plate surface - if flat - become significant for very close objects, roughly at less than 10-15 meters away (however, it is still dwarfed by the aberration created in the rest of the system). For the rear plane-parallel plate surface, the aggregate wavefront aberration is given by replacing the out-of-bracket factor n(n2-1)/I13 in Eq. 105 with -(n2-1)I2/n2L4, where the rear surface image distance I2 is given by I2=(I1+T)/n, T being the plate thickness. For both surfaces combined, the aberrations of plane-parallel plate, also as the P-V wavefront error at the best focus location, are given by:
for spherical aberration, coma, astigmatism, field curvature and distortion, respectively (note that the error for coma is one half of the P-V error). As before, each particular aberration alone is given by a product of the respective factor within the main bracket and the outside factor, in this case (n2-1)T/n3. Axial image shift caused by plane-parallel plate, as the separation between the object and final image formed by the second surface, is given by Δ=(n-1)T/n, thus independent of object distance. Note that it is independent of ray height at the plate only in the paraxial approximation, which means that this relation is strictly valid only for paraxial rays. The actual shift increases with the ray height. For the marginal ray, it is given by ΔM=Δ+(n2-1)T/8F2n3, with the shift differential representing the longitudinal spherical aberration (overcorrection) induced by the plate (for any ray, the added shift is obtained by replacing F-number for the marginal ray with the one corresponding to the ray, given by the ratio of its original back focus length from the front plate surface to its height at this surface). According to Eq. 105.1, plane-parallel plate alone introduces zero aberrations for object at infinity. As for the Schmidt surface, the only appreciable aberration it introduces is spherical, needed to cancel spherical aberration of the mirror. With spherical aberration cancelled for the optimized wavelength, the remaining lower-order aberrations of the Schmidt camera are residual spherical aberration for non-optimized wavelengths, so called chromatic spherical aberration, or spherochromatism, and image field curvature.
Chromatism of plane-parallel plate is given as longitudinal shift by
ιT/n2,
with ι
being the index differential, and by -ιhT/Ln2
for lateral displacement (with h/L equaling
α, it can be also written as -ιαT/n2).
Spherochromatism
It is evident from
Eq. 101-101.1 that Schmidt corrector can cancel spherical aberration
of the mirror only for a single wavelength, for which the corrector
shape will produce the exact amount of selective wavefront retardation
needed for the cancellation. For other wavelengths, the amount of
wavefront retardation will deviate below and above the optimum,
resulting in spherical aberration. Best focus location for the aberrated
wavelengths is the one with the highest peak diffraction intensity. For
the longitudinal spherical aberration normalized to This is valid as long as the magnitude of spherochromatism is relatively low. The more of non-optimized wavelengths exceed 1/2 wave P-V, the more of a factor becomes a shift of the PSF peak away from the point of minimum wavefront deviation. The shift begins as spherical aberration at the best focus exceeds 0.6 wave P-V, with the PSF peak moving from the mid focus (l=1, NZ=0.707) for errors of 0.6 wave P-V and smaller, to the location of the smallest geometric blur (l=1.5, NZ=0.866) at 1 wave P-V. Since errors of these magnitude are not uncommon - particularly for the violet end, where the error is also the largest - systems having significant spherochromatism will likely benefit from moving the neutral zone above 0.707 mark. The optimum height is one at which the increase in error for non-optimized wavelengths under 0.6 wave P-V, due to moving the neutral zone higher, is most overcompensated by the decrease at the wavelengths with larger error. If, for instance, the error in violet h-line is 1 wave P-V, the optimum neutral zone height will be roughly midway between 0.707 and 0.866.
Another factor to consider is the
effect of central
obstruction on the spherochromatic error. Large central obstructions
do significantly reduce the RMS wavefront error of spherical
aberrations, when its magnitude is significant. This implies that the
relative error for the far vs. near non-optimized wavelengths in such
case diminishes in the systems with large central obstruction. Large
central obstruction also suppresses the above mentioned PSF peak shift.
Thus actual gains from optimizing for neutral zone height may be
relatively small.
Wsc= ιŵD/512(n-1)λF3
(106)
with
ι
being the index differential vs. optimized wavelength given by
ι=no-ni,
no
being the optimized wavelength index, ŵ
is
the above
error factor for the spherical aberration defocus with
Λ=2N2,
N being the neutral zone position (0 to 1), D the aperture
diameter, n the corrector refractive index and F the
mirror focal ratio. Negative index differential for shorter
wavelengths makes the wavefront error negative, or over-corrected, while
the longer wavelengths are under-corrected. The usual practice, based on raytracing preference of the minimum blur size, is to
put the neutral zone at √0.75
the radius. However, the smallest wavefront error - and that is what
counts - is with the neutral zone at
√0.5
the radius (FIG. 169).
The blur diameter is determined at the point
of maximum surface slope, which is located either at the edge, or at a
point below
the neutral zone. Relative heights of these two points, in units of
the normalized
pupil radius, are given with ρ1=1
and ρ2=(Λ/6)1/2. The corresponding ray deviation from horizontal direction is given by:
in radians, ρi
being one of the two heights of the maximum ray deviation. The
greater deviation δmax
determines maximum size of the chromatic blur. It is
identical at either point for
Λ=1.5
(0.866 neutral zone), while greater at the edge (ρ=1) for
Λ=1 (0.707 neutral zone).
The deviation - and the geometric blur size - is at its minimum value
for
Λ=1.5 (0.866 neutral
zone), smaller than for
Λ=1 (0.707 neutral
zone) by a factor of two. Actual sphero-chromatism, as mentioned,
measured by the nominal wavefront error in the non-optimized wavelengths, is
at its minimum in the latter, smaller by a factor of 0.459 than for
0.866 neutral zone placement.
FIGURE 170: Being at the distance equal to mirror's radius of curvature, any point
on the back of corrector is re-imaged to the opposite side after
reflection from the mirror. This geometry determines blur diameter
formed by non-optimized wavelengths in the focal plane. Blur size is
determined by the maximum angle of deviation
δ from the horizontal
for the optimized wavelength, which determines maximum angle of
deviation for non-optimized wavelengths, varying with a factor of
ι/(n-1) -
ι being
the index differential - than the zero-blur angle of deviation of the optimized wavelength. The
dependence on this geometric criterion has lead to the common erroneous
view that 0.866 NZ location, giving the smallest geometric
blur, also results in the lowest level of sphero-chromatism. Both,
diffraction and P-V/RMS wavefront error criteria favor 0.707 NZ
location.
Chromatic blur diameter is given by:
δmax
being the maximum ray deviation,
ι
the refractive index differential vs. optimized wavelength and f
the mirror focal length. For given corrector's focus factor
Λ, the relative
ray height at the focus location can be expressed in terms of the ray height at the pupil of normalized
to unity radius ρ
as:
Thus, chromatic blur diameter can be expressed in terms of the
corresponding ray height in the pupil
ρm
resulting in the maximum ray height at the focal location
Λ as:
with, as mentioned,
ρm=1
for
Λ=0, 1,
and 1.5;
for
Λ=2,
ρm=1/√3.
EXAMPLE: The same 200mm
f/2 Schmidt
camera from the previous page, with BK7 corrector and 0.707 neutral
zone. The index differential
ι
for the blue F (486nm) and red C
(656nm) lines are 0.00388 and 0.00418, respectively, and the spherical
aberration factor ŵ=0.25 (best focus location). According to Eq.
106,
Wsc=ιŵD/512(n-1)λF3, the respective wavefront errors of spherochromatism, in units
of the wavelength, are 0.19 and 0.15 wave P-V.
With the maximum ray deviation angle in the optimized
wavelength
The remaining 3rd order aberration of the Schmidt camera is
field curvature introduced by the
mirror. The radius of field curvature equals mirror's focal length,
which makes it quite strong in smaller, fast Schmidt cameras, considering
generally wide fields. How much of the curvature-induced defocus is
acceptable can vary significantly with the specific purpose and criteria,
but generally shouldn't be making the seeing blur much larger. As an
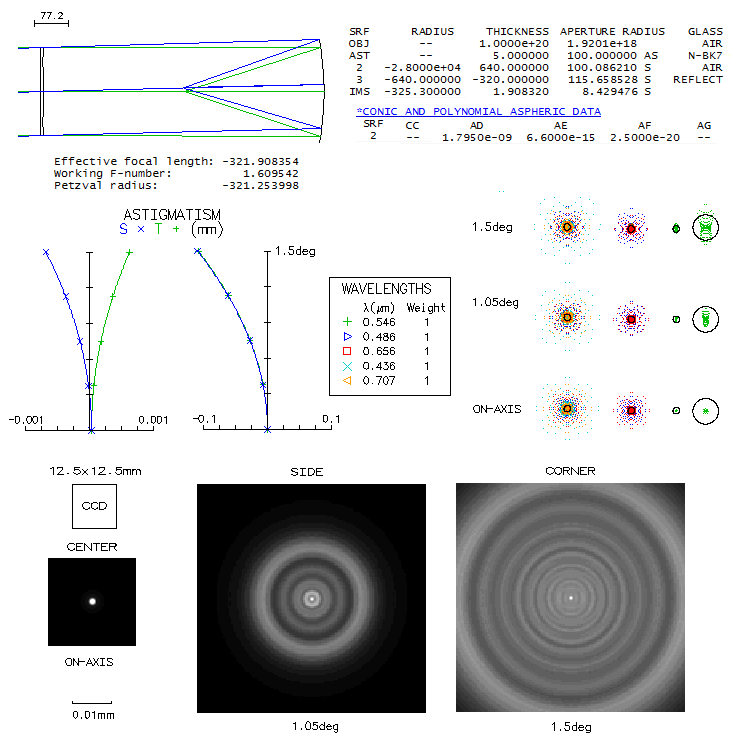
illustration of how flexible "acceptable" can be, here's a 200mm f/1.6
Celestron Schmidt camera with 12.5x12.5mm CCD ship and no flattener.
A forum amateur posted images of starry fields made with it, finding
them acceptable (they do look OK, at least on the first sight). The
error, however, is nearly 5 waves P-V of defocus near the side, and
full 10 waves in the corner. Diffraction images below illustrate the
effect on point image size (5-wavelengths polychromatic, even sensitivity).
Astigmatic plot at left is along the best image curvature, showing
slight residual astigmatism (0.0013mm longitudinal astigmatism implies
0.013/8F2, or less than 0.12 wave P-V of astigmatism at
1.5° field radius). At right is astigmatic plot vs. flat field,
showing the same field point nearly 0.11mm in defocus vs. field center
(it translates to 0.11/8F2 - same formula as for astigmatism - or
nearlu 10 waves P-V wavefront error of defocus).
Over the best field, there is no deformation of the diffraction image
to speak of. On the flat field, diffraction blur expands to about 1/30 mm
near the CCD side, and about twice as much in the corner. Taking
the usually quoted 1/40 mm
as the largest acceptable, this explains why the images didn't look as
bad as the wavefront error alone would imply. However, angularly it doesn't
look rosy: blur size close to the side is as much as 20 arc seconds, and
twice as much in the corner. Theoretical resolution limit for the
aperture is less than 0.6 arc seconds (it applies to a pair of nearly
equal in brightness, faint stars), with the average seeing FWHM
about four times larger. This implies that limiting resolution
is only roughly ten times the theoretical limit at the field side, and
twice as much in the corner.
Using best image surface
requires either curved detector surface, or field-flattener lens - a
simple plano-convex lens placed close to the focal point, flat side
facing the image, with the radius of curvature of the convex side given
by R=[1-(1/n)]f,
f being the mirror (camera) focal length.
The two significant aberrations induced by the lens are spherical and
coma. The faster and larger camera, the more significant image
deterioration. Since the lens is very close to the focal plane, and the
width of converging cone is small, radius term for the axial cone can be
neglected, and the wavefront error of lower-order spherical aberration
as the P-V error at the best focus is closely approximated by the aberration
of a plane-parallel plate (1st term in Eq. 105.1):
Ws = (n2-1)Td4/32n3L4
with n being the refractive index, T the lens center
thickness, d the height of the marginal ray at the front lens
surface and L the object distance, equaling the
front-surface-to-final-image separation, given for parallel plate by L=l-(T/n),
with l being the
front-surface-to-original focus separation (for a lens, it is slightly
smaller, due to the effect of the front surface radius). The wavefront
error is numerically positive,
which indicates that the form of aberration is under-correction
(negative at paraxial focus, and positive at the best focus location;
reversed for over-correction).
Due to typically large relative apertures of the Schmidt camera, abaxial
aberrations induced by the field flattener lens - particularly coma -
can also be significant, even with the flattener nearly touching the
image. The extent of lower-order aberrations can be determined from aberration coefficients
for general surface with displaced stop. An example of the Schmidt
camera with a simple singlet field
flattener lens, including aberration calculation and ray spot plots, is given in the
sub-aperture catadioptrics section.
Field flattener also increases camera's chromatism. Both coma and
chromatism induced by field flattener of this type can be minimized in
an integrated design, with optimized corrector separation (somewhat
closer to the mirror) and neutral zone location.
Alignment errors
Misalignment of the corrector - either
tilt or decenter - can create system aberrations. Corrector tilt alone (not combined with
decenter) does not induce appreciable point-image
aberrations. Decenter (i.e. lateral shift) of Schmidt corrector,
however, by effectively creating radially asymmetrical surface in the
aperture opening, induces coma. The P-V wavefront error of
coma caused by linear decenter
∆ is given by:
Note that this
amount of added coma remains constant throughout
the field.
Corrector decenter also induces astigmatism, but comparatively negligible with respect
to coma.
While originally intended to correct
spherical aberration of the sphere with the stop at the center of
curvature, Schmidt corrector is also used in other camera types, as well
as in arrangements with one- and two-mirror telescope configurations. Schmidt-Newtonian and
Schmidt-Cassegrain are the two most common telescope designs using
full-aperture Schmidt corrector.
Lensless Schmidt
An arrangement with spherical mirror with the stop at its
center of curvature - but without correcting lens - is called lensless
Schmidt. Coma and astigmatism are cancelled, and the P-V wavefront error
of spherical aberration is determined by the effective relative aperture
of the mirror, as W=0.89D/F3,
in units of 550nm wavelength, for the effective aperture D in mm
(W=22.6D/F3
for D in inches).
While attractive for its simplicity, as well as a field free
from coma and astigmatism, the configuration is effective only for relatively
slow systems. In faster systems, spherical aberration becomes excessive,
causing spread of energy resulting in significantly slower photographic speed than
that implied by the nominal relative aperture, loss in limiting
magnitude, contrast and resolution. The usual criterion sets acceptable
aberration level as determined by the smallest geometric blur equaling
0.025mm. With the smallest blur given by D/128F2, this sets the limit to
the lensless Schmidt relative aperture at F≥√D/3.2
for the effective aperture D in mm, or F≥√7.94D
for D in inches.
Plugging in the above wavefront error formula gives the
corresponding wavefront error of spherical aberration varying at this
level from 0.5 wave for D=100mm f/5.6 to 0.36 wave for D=200mm
f/7.9
system. This error level is significant, but it is considered acceptable
in a system intended mainly for photographic purposes. This, however,
doesn't mean it is comparable to a near-perfect system.
Let's consider a 150mm f/6.8 lensless
Schmidt. It suffers from 0.42 wave P-V of lower-order spherical
aberration. It has caused 84% of
light energy - the relative energy content of the Airy disc in a perfect
aperture - to spread into a circle more than three times the Airy disc
size, with the later now containing about 44%
of the energy. The adverse effect on photographic speed, limiting
magnitude and contrast level is not negligible. With respect to speed,
nearly halved amount of light in the Airy disc reduces its brightness
correspondingly, resulting in an effective f/9.4 system for stellar
imaging and small extended objects. Extended objects significantly
larger than the 84% energy spread circle still contain most of the
energy, hence are comparatively less affected speed-wise. However, the
energy scattered out of the Airy disc significantly lowers contrast
level and resolution of detail within these objects; it is comparable to
a system with 0.53D central obstruction.
Doubling the wavefront
error by further reducing the F number by a factor of 0.51/3,
to f/5.4, results in the 84% energy circle over six times the Airy disc
diameter, with less than 10% still contained within the Airy disc.
Performance of such system is comparable to an f/21.5 system speed-wise
on stars and small extended objects. Its first MTF resolution limit is
reduced to about 1/5 of that in a perfect aperture (which effectively
makes it only ~20mm in aperture in this respect), with some faint
resolution windows possible at higher resolution levels. Needles to say,
with nearly 1 wave P-V of spherical aberration, the contrast level is
very poor; it is comparable to that in a system with 0.83D central
obstruction.
Since the wavefront error of spherical aberration
increases inversely to the third power of the mirror F number,
relatively small gains in the nominal photographic speed and angular
field achieved by reducing medium to low speed apertures are, already at the point approximated by the geometric criterion
above, more than offset - and rather quickly - by speed and contrast losses resulting
from deterioration in image quality. If the 0.025 mm smallest blur
criterion is replaced by the more consistent - and more demanding - 1/4
wave P-V criterion, the corresponding minimum relative aperture for a
spherical mirror is given by F=(3.56D)1/3,
for D in mm. This means that lensless Schmidt shouldn't be faster than
~f/7, f/8 and ~f/9 for D=100, 150 and 200mm, respectively. Considering
required system length, it wouldn't be practical at apertures exceeding
~100mm.
In all, the lensless Schmidt, as
expected, except in slow small-aperture systems, cannot substitute for the actual Schmidt camera, or even come
close to it in its performance level. |
FIGURE 169: Spherochromatism in
a 200mm f/2.4 Schmidt camera. While the corrector with 0.866
radius neutral zone brings the circles of least confusion for all
wavelengths to a common focus (left), corrector with the
neutral zone at 0.707 of the radius, brings diffraction (best) foci
for all wavelengths to a common focus. Despite twice as large linear
blur, and identical longitudinal aberration (note that the
horizontal scale is larger for the 0.707NZ plot, but the actual LA
is identical for both), the wavefront error of spherochromatism in
the latter is less than half that in the
former. The 0.025mm scale is for the geometric blur size. Note
that this wavefront-specific error changes if residual spherical
aberration is present in the system; in effect, it will sway all the
curves to one or the other side worsening correction level for the
optimized wavelength and those wavelengths that were bent in the direction
in which the optimized wavelength's plot is swayed,
while improving correction of those on the other side.
For
any given aperture D, focal ratio F and glass type, the
ray height in the image plane changes with ρ
