◄ 10.2.2.3. Schmidt-Newton telescope   ▐    10.2.2.4.1. SCT off-axis aberrations ►
 

10.2.2.4. Schmidt-Cassegrain telescope (SCT)

Among the most popular commercial designs, the Schmidt-Cassegrain telescope (or SCT, FIG. 174) owes its success mostly to the possibility of relatively inexpensive commercial production of a well-performing Schmidt corrector, particularly in combination with two spherical mirrors. The road for the SCT commercial production was paved by Tom Johnson (Celestron) who, back in the 1960-ties, pioneered a method for corrector's mass-production. Following text is limited to the basic arrangement consisting of the full aperure Schmidt corrector and two mirrors; arrangements with sub-aperture corrector, including Celestron Edge, can be found here.

Optical effect of the corrector on the system parameters is small, but not negligible. It slightly increases the marginal ray height on the primary, as determined by its refraction angle δ (Eq. 107), with this ray being then directed toward a different focus focus point, as a result of corrector's interference.

With, say, 200mm f/2 spherical primary, combined with a 0.707 neutral zone corrector at σ1=0.4R1 (primary's radius of curvature) in front of it, marginal ray on the primary will be only ~0.23mm higher (for ~0.71 corrector power in an all-spherical arrangement). The two, corrector and primary, "act" as a prolate ellipsoid (K~-0.71), nearly 200.5 mm in diameter, with only slightly extended marginal focus. Since it still retains ~29% of the original D(mm)/32F longitudinal spherical aberration, in order to find out secondary magnification we need to trace the 0.707 zone ray, the only one whose height and orientation after passing the corrector and primary didn't change, and to whose focus the rest of rays will be directed after reflection from the secondary.

Taking the 0.707 ray as marginal, the primary becomes 141.4mm diameter f/2.79 mirror (the 0.707 ray focuses at the mid point of the original longitudinal defocus, 1.56mm inside the primary's paraxial focus). Slightly shorter focal length - and the corresponding radius of curvature - increase the effective secondary-to-primary radius of curvature ratio ρ from 0.3125 (in an f/2/10 mirrors-only system with paraboloidal primary) to 0.3137, with the relative ray height at the secondary in units of the aperture radius k reduced from 0.25 to 0.2471, and the resulting secondary magnification m reduced to ~4.7.

Applying this magnification value to the effective 200mm f/1.992 primary results in a final f/9.38 system. So, if the two mirrors without corrector would form an f/10 system, optical effect of the corrector changes it into ~f/9.4. In order to have an f/10 system with an f/2 primary, the secondary needs to be slightly more (~1.5%) strongly curved, thus with the R2/R1 radii ratio ρ~0.308, for the secondary magnification m=~5.05. The relative back focal distance in units of the primary focal length is only slightly reduced, from 0.5 to η~0.49.

Aberration-wise, there are two significant differences between the SCT and all-reflecting Cassegrain varieties. One is that the SCT can be made free from both, coma and astigmatism, while an all-reflecting arrangement can only correct for one. On the other hand, the Schmidt corrector induces some sphero-chromatism. Image below shows Celestron C11 f/1.9/10 SCT configuration in comparison with the same configuration as a solid Schmidt SCT, and clasical Cassegrain.

Raytrace shows similar output for the standard and solid SCT, except that the latter has significant lateral color error. All-reflecting Cassegrain has significantly lower off axis aberrations and zero chromatism, but twice stronger best image field curvature. At 0.25° degrees off astigmatism is just a tad larger than coma, becoming dominant farther off.

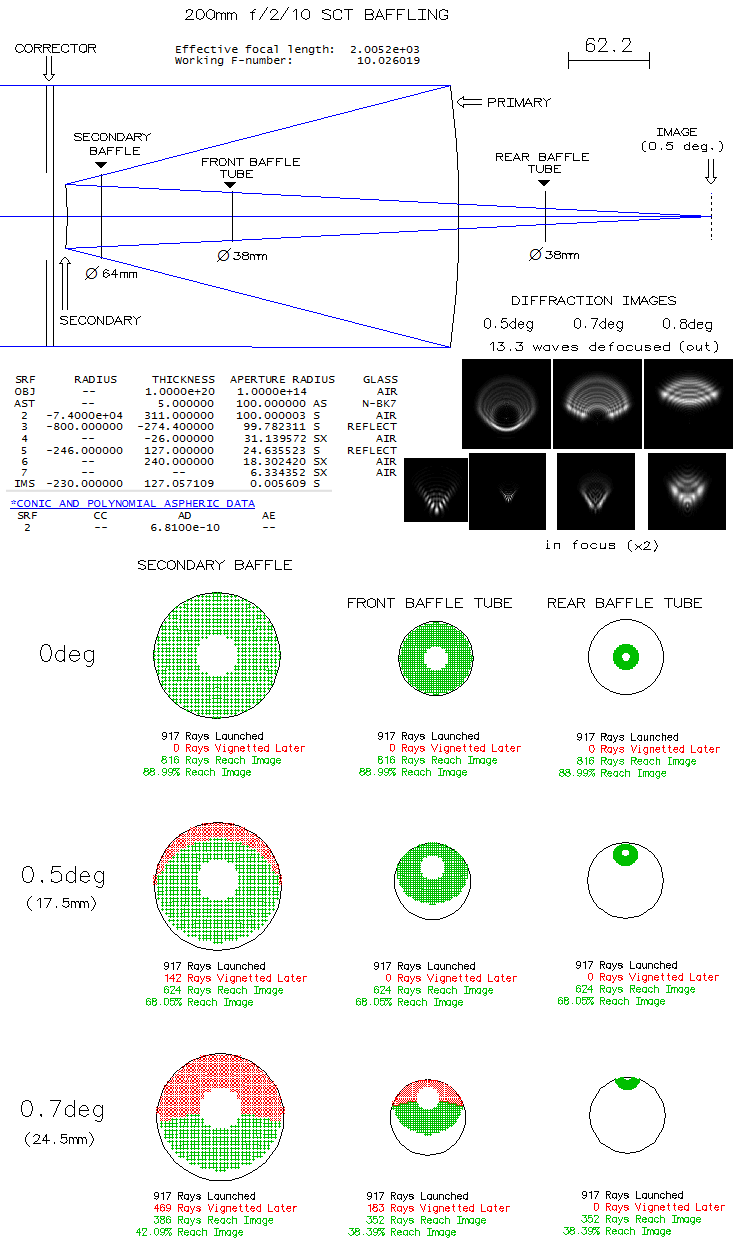
SCT BAFFLING (FIELD ILLUMINATION)

In order to protect the final image from both direct light from the sky and various forms of stray light, SCT uses internal baffle system consisting of the secondary baffle and baffle tube (it can be enhanced with a tube shield, but it does not affect field illumination). Image field below shows the effect of this internal baffle system on image illumination in what can be considered to be the standard SCT design for 8-inch aperture, with 34% central obstruction (Celestron). Edge of both secondary baffle and front baffle tube opening are separated less than 1mm from the converging axial cone, with the final focus placed 127mm behind the baffle tube rear enhanced (as specified by Celestron). This produces vignetting as shown below. At 0.5° field angle vignetting at the secondary baffle is a bit over 6% (50 rays out of 816, which is the effective full illumination after taking 11% from the 927 rays launched), but it is inconsequential because the vignetting at the front baffle tube opening - of this same section of the cone - is already much higher, 21% (i.e. it would be just the same if there was zero vignetting at the secondary baffle). Field edge illumination of 76% (624/816 rays) is barely accepteble for imaging, and unnoticeable visually in general observing (little over 1/4 magnitude loss).

Minimum acceptable illumination for field edge is around 40% (1 magnitude loss) visually, and an 8-inch SCT drops close to that level at the 0.7° field angle. At this point, vignetting is effectively taking place at the rear baffle opening, which determines its level for field angles of about 0.6° and larger. At 0.8° illumination drops to 19%, and at 0.9° it is below 1%. Extending focus by 100mm increases illumination to 29% at 0.8°, it is unchanged at 0.7°, and drops to 68% at 0.5°. Axial beam is reduced by 32 rays at the secondary baffle, and another 56 rays at the front baffle tube opening, totaling 88 rays. It is nearly 10% of the initial 917 rays (w/o obstruction), amounting to 5% effective aperture diameter reduction. To prevent this, both baffle openings should be larger, at the secondary by about 2%, and at the baffle tube front by about 5%. In general, vignetting in an 8 inch SCT is very similar to that in the C9.25. The latter also shows that back focus extension has little effect on the linear field illumination.

Significant vignetting can be detected by placing defocused image of a star close to field edge. The shape of defocused star will resemble shape of the beam footprint on the last baffle opening: round if no vignetting occurs, and increasingly squeezed toward field edge with the increase in vignetting (diffraction images). Significant vignetting also changes the in-focus pattern, with it becoming different in its form and generally larger due to the effectively reduced aperture (in-focus patterns are magnified, and the 0.5° in-focus pattern is additionally magnified to show its form).

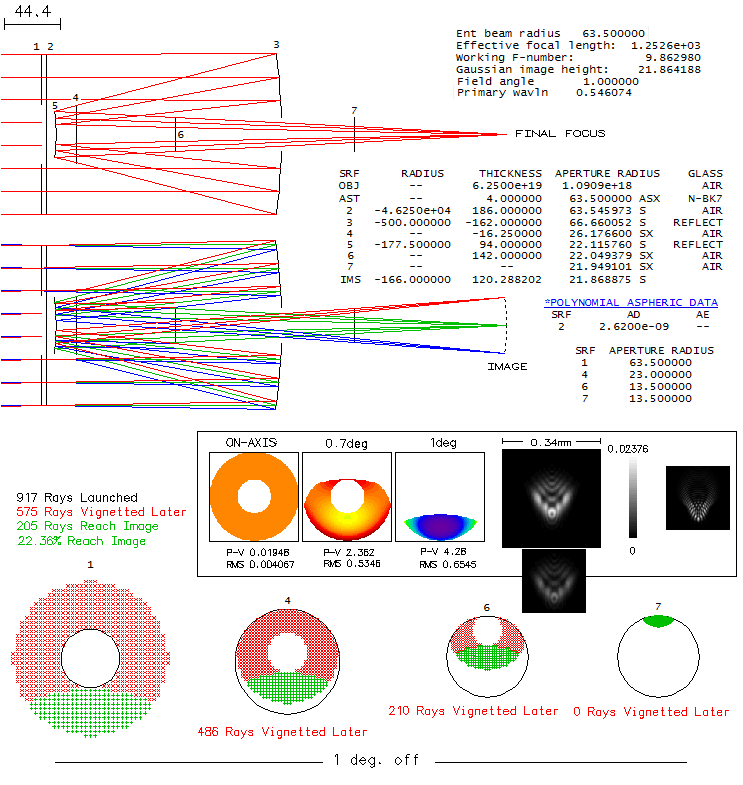
As another example, Celestron C5. Despite significantly smaller rear baffle tube opening (27mm inside diameter), it has illuminated field similar in size to that in 8-inch SCT linearly and, due to its smaller image scale, somewhat larger angularly. Illumination over linear field in the C5 is somehat lower.

Follows overview of SCT axial aberrations, spherical (as a sum of spherical aberration contributions of its three elements) and spherochromatism.
 

SCT spherical aberration

The only significant monochromatic aberration introduced by the Schmidt corrector in collimated light is spherical. Its purpose is to offset spherical aberration on the two mirrors, resulting in a spherical-aberration-free system. Thus, the P-V wavefront errors for lower-order spherical aberration at the best focus for an SCT system can be written as:

with scr being the corrector spherical aberration coefficient, d the pupil (aperture) radius and the mirror aberration coefficient sM being the sum of the individual mirror spherical aberration coefficients, sM=s1+s2. Individual mirror coefficients for object at infinity are the same as for a two-mirror system alone (Eq. 9.2 and Eq. 9 for the primary and secondary, respectively), given by:

for the secondary, with K1 being the primary conic, R1 the primary radius of curvature, k the height of marginal ray at the secondary in units of the aperture radius, m the secondary magnification and ρ=R2/R1, the secondary radius of curvature in units of R1.

Note that in order to be able to directly add the two coefficients, the secondary aberration coefficient had to be corrected for the difference in apertures by multiplying it with k4 factor, the relative height of marginal ray at the secondary in units of the ray height at the primary. The two forms for the secondary aberration coefficient have parameters interchangeable through k/ρ=kR1/R2=(m-1)/m=1-(1/m).

Thus, the system P-V wavefront error at the best focus can be written as:

with P being the needed corrector power to cancel system spherical aberration, and ss={}/4R13 being the system aberration coefficient (the final {}D/2048F³ form comes after substituting d=D/2 and |R|=2f in the original relation for the aberration at the paraxial focus, {}d⁴/4R³, which is four times larger than at the best focus location).

Of course, for zero system spherical aberration, the aberration coefficient for the corrector scr, which is related to the corrector power P as scr=-P/4R13, needs to be equal to the sum of mirror aberration coefficients sM, and of the opposite sign. If the primary is spherical, to cancel its aberration alone, the corrector aberration coefficient needs to be scr=-b/8 (with the aspheric term b=2/R13, it comes to scr=-1/4R13, same as the spherical primary, but of the opposite sign). The corrector with this value of the aspheric term is said to have a unit power P. In such arrangement, for cancelled spherical aberration of the system, the secondary mirror conic needs to be K2=-[(m+1)/(m-1)]2, same as in the classical Cassegrain. With both, primary and secondary spherical (K1=K2=0), needed power P of the corrector for zero system spherical aberration is (from Eq. 113.1) P=1-k(m-1)(m+1)2/m3. For the typical f/2/10 SCT with k~0.25 and m~5, P~0.71, i.e. needed corrector strength, or depth, is about 71% of that needed to correct the primary alone. In terms of the F-ratio, this corrector has the strength needed to correct some 12% slower primary.

In general, for any combination of conics, needed corrector power to cancel spherical aberration of two mirrors is determined by a value of the sum of opposite aberrations contributions of the primary and secondary relative to spherical aberration of the primary alone. Thus, it can be written as P=1-(s'2/s'1), with the aberration contribution of the secondary s'2 in proportion to k[K2+(m+1)2/(m-1)2](1-1/m)3, and aberration contribution of the primary s'1 proportional to (K1+1). The prime notation is to differentiate the proportionate relative contributions from the corresponding actual aberration coefficients s1=s'1/4R13 and s2=s'2k4/4R23.

Thus, the lower-order aspheric parameter A1 for the corrector in a Schmidt-Cassegrain system can be, analogously to the Schmidt camera, written as A1=b/8(n'-n), but with the corresponding aspheric coefficient b changed in proportion to the needed corrector's power, as b=2P/R13. Reduction of the 5th order aspheric parameter of the SCT corrector, A2, relative to the value for primary alone, is typically greater than that of A1, due to significant higher-order spherical aberration of opposite sign generated at the secondary as a result of relatively close object (i.e. image of the primary) distance, as well as due to reduction in the higher-order aberration resulting from reduced corrector separation (i.e. height of marginal ray at mirror surface). For spherical secondary and typical 8" f/2/10 SCT configuration with σ~0.4, the parameter, given by A2=b'/16(n'-n), with the higher-order aspheric coefficient b' approximately 1/6 of that needed for primary alone (with the stop at the center of curvature), or b'~[1-(k6/ρ5)]/R15.

Thus, the higher-order corrector's power in the typical commercial unit is only ~0.16 of that needed to correct higher-order spherical aberration of a comparable f/2 Schmidt system. The parameter changes for different values of σ1 approximately in proportion to σ1/0.4, thus the generalized approximation for b' can be written as b'~2.5σ1[1-(k6/ρ5)]/R15.

For closer objects, spherical aberration coefficients for all three, corrector, primary and secondary change (it is negligible for the corrector), disturbing presumed  near-zero balance for distant objects, and resulting in spherical aberration. The chage of aberration contribution on the two SCT mirrors is similar to that in all reflecting two-mirror systems (Eq. 92). Main difference is with SCT systems that focus by moving the primary. Here, the error induced by a relatively small object distance is in part offset by under-correction induced by refocusing, which requires an increase in mirror separation.

More specifically, reduced object distance lowers under-correction of the primary, and increases over-correction of the secondary. That makes the system over-corrected; the increased mirror separation needed to bring the focus point to its fixed location diminishes the effective diameter of the secondary, reducing over-correction induced by it, and by that the overall system over-correction as well. This makes a typical commercial SCT better suited for terrestrial observations than a similar system with fixed-mirror focusing. More details on this subject are given in 11.5.2. SCT focusing errors.
 

SCT spherochromatism

Spherochromatism in the SCT originates at the corrector, whose corrective power is optimized for one - usually green/yellow - wavelength. Since shorter wavelengths refract more strongly, and the longer ones refract more weakly, the effective corrector power increases toward the former, and decreases toward the later. With the combined spherical aberration of the two mirrors being undercorrection, this means that shorter wavelengths (blue/violet) will be overcorrected, and the longer ones (red) undercorrected. This wavelength-dependant spherical aberration increasing with the refractive index differential vs. optimized wavelength is the only source of chromatism in a SCT.

Given aperture and F#, SCT spherochromatism is proportional to the relative power of the Schmidt corrector P. In other words, to the relative value of the aspheric term b needed to cancel spherical aberration of the system. It can be written as:

with bs being the aspheric factor - or the corrector's spherical aberration coefficient - needed to correct for spherical aberration of the primary alone. As mentioned, b=2/R13, from the general form of the aspheric coefficient b=2n[(m+1)/(m-1)]2/R13, for mirror magnification m=0 (object at infinity) and index of incidence n=1.  Aspheric coefficient cancelling the aberration of a spherical mirror is bs=-b/8=-1/4R13, while  that for an SCT system,  equal to its aberration coefficient scr, is bSCT=-P/4R13, where P is the corrector power, positive in sign.

The P-V wavefront error of spherochromatism for a particular SCT arrangement is obtained by multiplying relative power of its corrector (Eq.  118) with the wavefront error for the unit power corrector (Eq. 106). For the transverse aberration (ray spot diameter), the relative power is to be multiplied with the transverse aberration for the unit power corrector (Eq. 107.1) and the SCT secondary mirror magnification.

In general, SCT spherochromatism is low. For a typical commercial ~f/2/10 version, with both mirrors spherical, k~0.25, σ~0.4 and m~5, relative corrector power ~0.72, and 0.866 neutral zone placement, the red (C-line) and blue (F-line) geometric blurs are still within the Airy disc. For the 0.707 radius neutral zone placement (FIG. 175), the blurs are doubled, but the wavefront error halves for the lowest chromatism level achievable with the Schmidt corrector.

Residual spherical aberration in the system will alter spherochromatic error due to the increased error in the optimized wavelength (FIG. 176).

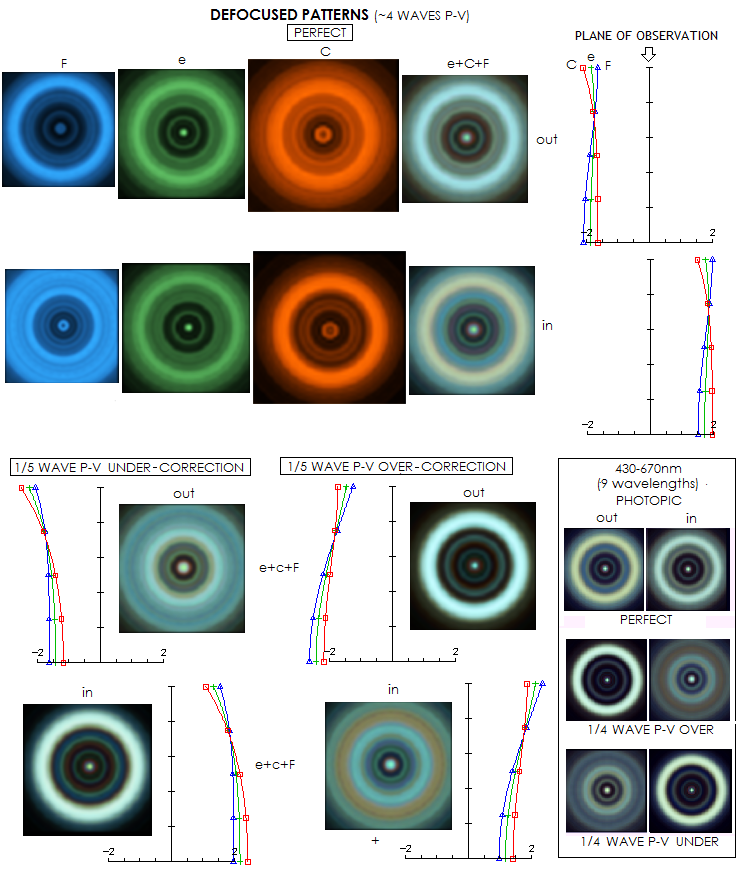
Since an SCT near-perfectly corrected for spherical aberration have blue wavelengths overcorrected, and red wavelengths undercorrected, a residual of, say, 1/4 wave P-V wavefront error of overcorrection in the optimized wavelength will increase spherochromatic error in the blue, and reduce it in the red (the plots are for a typical f/2/10 8-inch SCT with spherical mirrors). If the residual spherical is relatively significant, spherical correction in the red is likely to be actually better than in the optimized wavelength.

Consequently, the instrument will have more or less pronounced chromatic imbalance, with the negatively affected portion of the spectrum (blue/violet wavelengths in this example) possibly showing noticeably inferior chromatic correction in both, visual observing and imaging.

SCT STAR TEST

Presence of spherochromatism to some extent alters out of focus SCT images. As simulations for 200mm f/2/10 SCT show below, non-optimized colors are positioned differently with respect to the plane of observation. In some cases, it results in their diffraction patterns, superimposing one over another, being significantly different in shape, and that causes the compounded defocused pattern to become not only colored to some extent, but possibly also somewhat different in shape.

For better clarity, only three colors are used, blue F-line (486nm), green-yellow e-line (546nm) and red C-line (656nm). Defocused patterns are shown for each wavelength and combined (even sensitivity). The out of focus patterns are similar in shape, producing a whithish combined pattern. The inside focus pattern for the F-line is different, causing appearance of coloration - predominantly yellow, but hints of other colors too - in the combined pattern. Bellow, combined patterns in presence of 1/5 wave P-V of spherical aberration show different patterns of coloration for over- vs. undercorrection. Plugging in 9 wavelength and photopic sensitivity (box at right) shows similar defocused patterns. Since spherochromatism, all else equal, scales with the aperture, smaller SCTs will have less noticeable color effect, and larger SCTs more. Also, this is for 0.707 neutral zone position; with 0.866 neutral zone, which results in 2.5 times higher spherochromatism, the effect would be noticeably more pronounced.

Follows an overview of the SCT off-axis aberrations, after a quick look at the properties of the standard SCT with an off axis mask.

EFFECT OF OFF AXIS MASK ON 11-INCH STANDARD SCT

Off axis mask can be used with large-aperture SCTs in conditions of strong atmospheric turbulence, in order to significantly reduce its negative effect on image quality. The obvious negative is the reduction in aperture, which is assumed to be at least partly compensated for by significantly improved wavefront quality. There are, however, some additional, relatively minor negatives.

Since the mask allows light to use only the upper portion of the optical train, colors are unwrapped and widely separated. Due to the very slow focal ratio, it is of little consequence if observing plane nearly coincides with the best image surface. The problem is, this surface is tilted, in this case by 9 degrees, which in the image plane perpendicular to optical axis (i.e. for unaccommodated eye) causes not only lateral deformation in the optimized color, but also lateral chromatic dispersion.

Bottom spots and images show this effect at the edge of the widest field possible with a 2-inch eyepiece barrel (best image surface tilt is slightly smaller, at 8 degrees).
 

◄ 10.2.2.3. Schmidt-Newton telescope   ▐    10.2.2.4.1. SCT off-axis aberrations ►

Home  |  Comments