|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
8.1.3. Aberrations of the Newtonian reflector diagonal flat
The role of Newtonian diagonal flat mirror is to divert light
converging from the primary to the side, so that the image forms outside
the incoming light, and can be observed without obstructing
it (except for the relatively small obstruction by the diagonal flat). Perfectly made diagonal flat doesn't induce optical aberrations; its
only effects are: (1) usually small reduction in light transmission, equal to
(1-ο2)r,
with r being the diagonal reflectivity ratio, and
ο
its relative diameter in units of the aperture, and (2) worsening of the diffraction
induced imaging error
due to the effect of central obstruction.
Fast Newtonian telescopes usually have the flat "offset",
or slightly shifted from the strictly centered position away from the
focuser and toward the mirror, both directions by ∆=(D-V)/4[F-(1/16F)]D,
in units of the diagonal flat's minor axis, where D and V are the
aperture diameter and fully illuminated image field diameter, respectively,
F-(1/16F) is the actual mirror focal ratio (when depth of
sagitta is deducted from the focal length), and F is the
conventional mirror focal ratio number F=f/D (offsetting amounts to sliding the surface downward along the inclination
angle by √2∆).
For all practical purposes, a simplified form ∆~(D-V)/4FD, or
(D-V)/4f, in units of the minor axis (f being
the mirror focal length), is just
as accurate.
In order to distinguish this collimation mode from
one in which diagonal moves only axially (unidirectional
offset), it is referred to as bidirectional diagonal offset (BDO). Derivation of the relation for diagonal's
bidirectional offset ∆
is given below the illustration on FIG. 117., as well as
relations between the basic parameters.

FIGURE 117: Needed diagonal bidirectional offset calculation is
determined by the known parameters: it is either the primary and
desired fully illuminated field, when needed diagonal size is also
obtained (1),
or the primary and diagonal size, with the resulting fully
illuminated field (2).
Shift value also changes with the eye-to-diagonal distance along the
focuser axis (3). The geometry determining needed offset value is
based on several parameters: mirror focal length
f,
mirror-to-diagonal separation S, diagonal-to-focus separation
H, diagonal-to-apex (apex being the point of
convergence of the lines connecting top and bottom of the two
mirrors) H',
mirror sagitta z and fully illuminated field
diameter V. Needed relations in (1) in are derived using three linear
functions: for the diagonal surface, f(d),
and for the top and bottom side of the extended cone,
f(t)
and f(b),
respectively, in (2) from similar triangles (shaded
gray), and in (3) from the identity of apparent angles over
at
and ab
sections of the major axis.
The fully illuminated field diameter V depends
on the flat's minor axis A
and flat-to-focus separation H, as given by V=[(F-1/16F)A-H]/[(F-1/16F)-(H/D)].
Again, the difference is practically negligible when the relation is
simplified to V~(FA-H)/[F-(H/D)]~[A-(H/F)]/[1-(H/f)].
Note that this gives fully illuminated field diameter in the horizontal
plane, before the offset; with the diagonal offset, the field size in
this plane is slightly reduced, due to the minor axis shift downward. Numerically negative result for V indicates too small
flat size for its location. Substituting V into the above
relation for the offset ∆ gives, after consolidation, more
useable offset formula with all the factors known, ∆=(D-A)/4[(F-1/16F)D-H],
in units of flat's minor axis A.
Replacing the actual mirror focal ratio F-(1/16F) with the
conventional focal ratio number F doesn't make appreciable
difference in the result. It leads to the final flat's offset formula -
for eye at the apex point -
as an actual shift away from the focuser and toward the mirror, as
illustrated above:
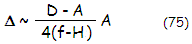
If the diagonal-to-primary separation (f-H)
is denoted as S, the relation simplifies to ∆~(D-A)A/4S.
Offsetting Newtonian diagonal flat doesn't
influence image quality, but evens up field illumination and makes
collimation easier, by centering the flat in the focuser opening
(for near-minimum size diagonal flat, offsetting may also prevent a small
light loss at the field center).
As the above illustration shows, this bidirectional
offset value applies when the vantage point (location of the eye while
collimating) is at the tip of the cone formed by extending lines
connecting edges of primary and diagonal. For other vantage point
heights, required bi-directional shift, derived from the equality of
apparent angles of the two sections of diagonal's major axis on opposite
sides of the focuser axis (identical in form to that preceding
Eq. 74, for
unidirectional offset) is also given by ∆=(Hi2+A2)/2,
Hi being the vantage point height above the diagonal
(fully illuminated field also becomes slightly decentered, with the
decenter equaling the shift increase). This means that the diagonal
offset in either bidirectional or unidirectional collimation mode is
identical for given diagonal-to-eye separation prior to commencing the
procedure
Most, if not all
formulas, as well as online calculators, give the BDO shift value for
collimating from the tip of extended cone, but that condition usually is not
specified.
Minimum diagonal size (minor axis) to transmit
the entire axial cone is given by Amin=H/F,
H
being the diagonal-to-focus separation (note that, due to the conical form of
the converging cone, the major axis needs to be slightly larger than
√2Amin,
specifically [1+1/(4F2-1)]√2Amin;
this is however, of no significance in regular Newtonian systems).
At the minimum secondary size, field
illumination, normalized to 1 at the field center, is
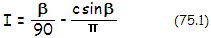
with cos(β)=c/2
and c=[1-(H/f)]FV/H,
where V is the image field diameter,
f
is the mirror focal length, and c is the axial center
separation of the cone cross section at the diagonal, in units of
diagonal's minor semi-axis. Quantitatively, c is determined by
the overlap of the marginal ray of an off-axis point away from
diagonal's edge in units of diagonal's minimum minor semi-axis. The
actual nominal overlap value for the marginal ray is given by Cmin=[1-(H/f)]V/2
for the minimum diagonal size Amin,
and for a larger diagonal A
by CA=[(1-V/D)H/2F]-(A-V)/2.
Following graph (FIG.
118)
shows illumination drop as a function of c, for a range of
relative diagonal sizes.
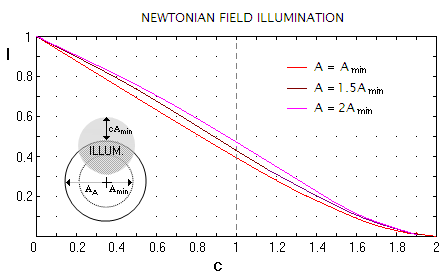
FIGURE 118:
Illumination I of off-axis image points in the Newtonian as a
function of the relative overlap of the marginal ray away from the
diagonal's edge in units of the cone radius (c), for the actual minor axis A
equal to the cone width at the diagonal (min. diagonal size), 1.5
and 2 times the minimum size. The illumination plot for the minimum
size diagonal is identical to
the MTF plot, since with c=2ν
Eq. 75.1 is identical to Eq. 57.
For c~1 and smaller, the plot changes linearly, with I=1-0.61c in
that range of c values. Drop in illumination is somewhat
slower for the larger minor axis A
sizes, but not significantly. Linear diameter of the fully
illuminated field is given by
I100=[A-(H/F)]/[1-(H/f)].
The lowest acceptable limit to visual edge illumination is for c~1,
with ~1 magnitude loss. The relative overlap ratio c in units of the
minimum diagonal's semi-axis is given by c=1-[A-(1-H/f)V]F/H.
EXAMPLE:
D=400mm f/4.5 Newtonian with diagonal-to-focus separation H=300mm,
minimum diagonal minor axis Amin=66.7mm
and actual minor axis A=80mm.
Diameter of fully illuminated field is I100=16mm
(0.5° angularly), relative overlap of
marginal ray for (V/2)=22mm off-axis point is c=1-[A-(1-H/f)V]F/H=0.35,
in units of the minimum diagonal's semi-axis.
Corresponding illumination for the minimum diagonal size is
I=(β/90)-csinβ/π=0.78;
from FIG. 74, gain in illumination for A/Amin=1.2
for c=0.35 is nearly 2%, with the appropriate illumination at 22mm
off-axis I~0.8, or nearly 80%.
As the plots show, field
illumination drop-off with a minimum size diagonal is not significantly
faster than with larger diagonal sizes. Even double the minimum size
diagonal gains only about 10% illumination at most, for the field points
with the converging cone overlapping the diagonal by about a length
equal to the minimum diagonal size minor semi-axis (c~1). The real
advantage of a larger diagonal is the size of fully illuminated field,
which is zero for the minimum diagonal size, and increasing in
proportion to diagonal size over the minimum size. Expressing the
diagonal minor axis in units of aperture diameter
D, as
a, and diagonal to
focus distance in units of the focal length, as
h, the field of full
illumination diameter is simply:
I100=(a-h)D/(1-h)
(75.2)
It can be also written as (AF-H)/(F-H/D), where A and H are the actual minor axis
and diagonal-to-focus distance, respectively. Evidently, for non-zero
field of full illumination, relative size of diagonal's mirror axis in
units of the aperture has to be larger than the relative size of
diagonal-to-focus separation in units of the focal length. The size of
fully illuminate field is strongly dependant on a-h and weakly
(and inversely) dependant on 1-h. However, increase in h
does not result in larger fully illuminated field with given diagonal,
since it decreases a-h. For instance, increasing the
diagonal-to-focuser separation from 0.15f
to 0.2f automatically increases the
minimum diagonal size by 0.05f/F=0.05D
which, depending on the diagonal's size over the minimum size at h=0.15,
will cause anything from significantly reducing field of full
illumination to stopping the aperture down at the diagonal.
Mel Bartels'
Newtonian diagonal
calculator is a handy tool for obtaining field illumination figures
in a specified Newtonian system. For computerized aid to
this and other design aspects of a Newtonian, see Dave
Keller's
NEWT freeware.
Wavefront error at the diagonal
is of particular interest with the
Newtonian design, the diagonal flat being its constitutive element. Of
course, perfectly flat diagonal won't induce any aberrations. In
reality, every diagonal is less than perfectly flat, and the result is
some form of wavefront deformation. Magnitude of this deformation
depends directly on the size and type of surface error at the diagonal.
In general, there are two types of diagonal surface error: (1) local
error, covering relatively small portion of its surface, and (2) error
smoothly distributed over the most, or all of the surface.
Any local surface error, be it a
single defect, any number of local errors scattered over the surface,
turned edge, or zone, will multiply in the wavefront by a factor of
√2,
or ~1.4. This is the consequence of its ~45° surface inclination, making
the diagonal about 30% less sensitive to local surface errors and
roughness than a "regular" mirror (FIG.
119).
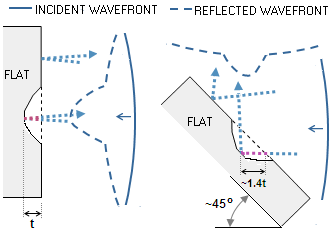
FIGURE
119: Left: When the direction of light after reflection is
nearly opposite to its incoming direction, local surface error
resulting in an air path difference of the thickness t
results in the wavefront P-V error of ~2t. This applies to
both, flat and curved surface mirrors orthogonal to the optical
axis.
Right: For the diagonal surface, the wavefront points after
reflection move in nearly orthogonal direction to that of wavefront
points coming onto the surface. Consequently, there is no
added compounding of the surface error in the wavefront. A surface error
creating an air path difference t will result in the
wavefront P-V error of ~1.4t, due to the actual surface error (i.e.
optical path difference) being enlarged by the ~45° position angle. Neither surface angles nor
angles of convergence in amateur telescopes result in appreciable
difference in added path difference vs. strict "orthogonal"
scenario. In general, Newtonian diagonal flat is less sensitive to
surface errors than main mirror.
For errors smoothly
distributed over diagonal's surface it is somewhat more complicated. The reason is that they, in general, change
the curvature of the wavefront so that part of the error induced can be
compensated by refocusing. As long as radii depth along the minor and
major axis are equal, there is no astigmatism induced, and the coma
wavefront error is very small in comparison to the surface error. It is
the difference in depth along the two radii that induces astigmatism,
not the surface P-V error itself (FIG.
120). Due to the
inclination angle, the final P-V wavefront error of astigmatism is ~1.4
times the difference in radii depth (when the radii are of the opposite
sign, as they are for the saddle surface form, the error is 1.4 times
the sum of their depths). This conveniently allows for obtaining good
approximations of the size of wavefront errors induced by these types of
surface error using quite simple calculations.
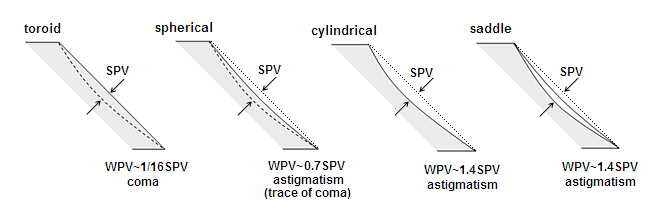
FIGURE
120: Four major types of smooth diagonal surface error, shown in
the side view along the major axis. The toroid with the minor
axis radius of curvature shorter by a factor of 2
than the major axis radius, has equal depths along both axes and
flat edges, resulting in near-zero astigmatism and P-V wavefront error
(WPV) of coma ~1/16 of the surface P-V
error (SPV). As the radii change toward equalization, depths
along the two radii grow uneven, and astigmatism induced to the
wavefront increases. Spherical surface has equal radii along
both axes, resulting in uneven edge with the center depth along the minor axis being
half of that along the major axis. The wavefront error induced - mostly
astigmatism, with traces of coma - comes from the difference in
radii depth, multiplied by a
√2
factor, due to the 45° angle of surface inclination. Thus, the
wavefront error is ~0.7 of the surface P-V
error (where the surface P-V error equals depth along the major axis,
twice the depth along minor axis). Surface change toward cylindrical and saddle
form result in further increase of the induced wavefront error of
astigmatism: it becomes equal to the surface error multiplied
by ~1.4 factor (cylindrical form has the best focus RMS error lower nearly 20%). Concavity vs. convexity of the surface deformation is
not a factor in the surface/wavefront P-V error relationship, and
neither is the axis - major or minor - along which are oriented
cylindrical and saddle form surface deformation. Also, the wavefront
error is independent of focal ratio and aperture. Note that the
diagonal surface error is for the area on the diagonal transmitting
the wavefront, normally somewhat smaller than the entire diagonal. Since
astigmatism changes with the square of aperture (i.e. beam diameter in this case),
and coma with the third power of it, typical diagonal will have even smaller
coma contributon.
The dependence of the size of
wavefront error caused by the diagonal flat on both, size and form of
the diagonal's surface error makes its actual performance level
uncertain, even if the nominal surface RMS error is known (the P-V error
is, as usual, pretty much meaningless). Safe policy is to go with the
worst-case scenario, expecting the surface error to multiply in the
wavefront by a factor of ~1.4. Since the dominant error for the above
smooth surface deviation forms is astigmatism (except toroid, which is
very unlikely to result from flat fabrication process, and the error it
produces is insignificant), the corresponding RMS error is smaller than
P-V error by a factor of √24.
Table below quantifies approximate degradation factor for three surface
P-V error values (wavefront errors are given in units of wavelength).
|
FORM OF DIAGONAL'S
SURFACE DEFORMATION |
P-V SURFACE ERROR |
P-V WAVEFRONT ERROR |
RMS WAVEFRONT |
STREHL DEGRADATION
FACTOR |
|
SPHERICAL
(RMS=PV/√24) |
1/4 |
1/5.6 |
0.036 |
0.95 |
|
1/6 |
1/8.5 |
0.024 |
0.977 |
|
1/10 |
1/14 |
0.015 |
0.991 |
|
CYLINDRICAL/SADDLE
(RMS=PV/√24) |
1/4 |
1/2.8 |
0.073 |
0.82 |
|
1/6 |
1/4.2 |
0.049 |
0.91 |
|
1/10 |
1/7.1 |
0.028 |
0.97 |
|
ROUGHNESS
(RMS~PV/3) |
1/4 |
1/2.8 |
0.119 |
0.57 |
|
1/6 |
1/4.2 |
0.079 |
0.78 |
|
1/10 |
1/7.1 |
0.047 |
0.91 |
|
ZONAL
(RMS~PV/3.3 for zones on the outer half of the radius) |
1/4 |
1/2.8 |
0.108 |
0.63 |
|
1/6 |
1/4.2 |
0.051 |
0.90 |
|
1/10 |
1/7.1 |
0.043 |
0.93 |
|
EDGE |
1/4 |
1/2.8 |
90% zone |
0.064 |
0.85 |
|
95% zone |
0.045 |
0.92 |
|
1/6 |
1/4.3 |
90% zone |
0.041 |
0.93 |
|
95% zone |
0.029 |
0.967 |
|
1/10 |
1/7.1 |
90% zone |
0.025 |
0.975 |
|
95% zone |
0.018 |
0.987 |
|
For minimum size diagonals
similar to turned edge on main mirror; for larger
relative
sizes, not affecting mid field performance |
|
LOCAL |
Wavefront P-V larger by a factor of ~1.4 than surface P-V. Varies
with the relative
size of area affected, generally significantly
smaller effect for given P-V error than P-V errors distributed
over entire surface |
Again, it is assumed that the P-V error is effective
over the area covered by a reflected cone of light. This is not much of
a factor with the last four deformation forms, but it can be significant
with smooth errors over entire surface. In that case, the effective P-V
error scales with the square of radius; if the P-V error is, for
instance, 1/4 wave over the entire surface, it will be only half as
large for converging cone that covers 70% of its diameter.
As noted before, the P-V error alone tells little
about specific effect of the diagonal on image quality. For the same 1/4
P-V value, the Strehl degradation factor can be anywhere from 0.95 with
spherical surface form (or even less with a local surface error), to
0.57 with surface roughness. With an excellent 0.95 Strehl primary, the
former would result in a 0.90 optics Strehl, and the latter in decidedly
substandard 0.54.
With star diagonals, converging cone
uses much smaller portion of the optical surface. Thus, even much larger
errors smoothly distributed over most of the surface have no appreciable
effect on wavefront quality. However, local surface errors,
especially in the mid-area, transmitting the light for the central
portion of the field, can have significantly greater effect. Another
difference is that star diagonal will scatter light for given
small-scale surface roughness to much smaller radius than Newtonian
diagonal, due to larger relative diameter of surface irregularities in
the reflected wavefront.
◄
8.1.2. Newtonian collimation
▐
8.2. Two-mirror telescopes
►
Home
| Comments
|