|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
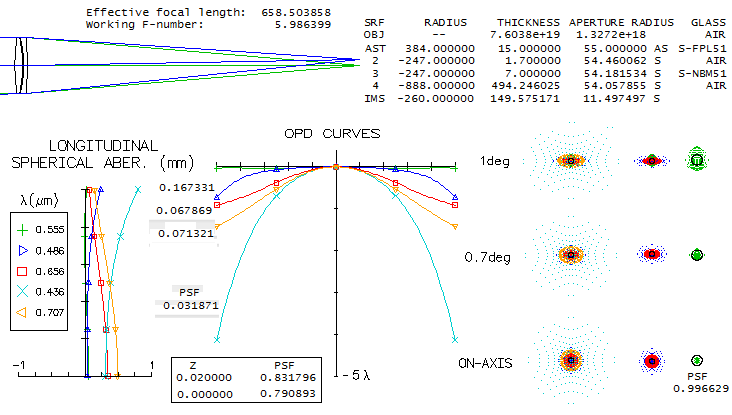
▪
▪
▪ CONTENTS ◄ 14.3. Observatory telescopes 14.4. Behind store window - Commercial telescopes
PAGE HIGHLIGHTS
For those like me, curious about what just about any telescope actually delivers, not so much because of the quality concern, but more to find out how it actually works (without breaking it open to look inside :), that is just a treat hard to resist. The raytrace program used is OSLO EDU.
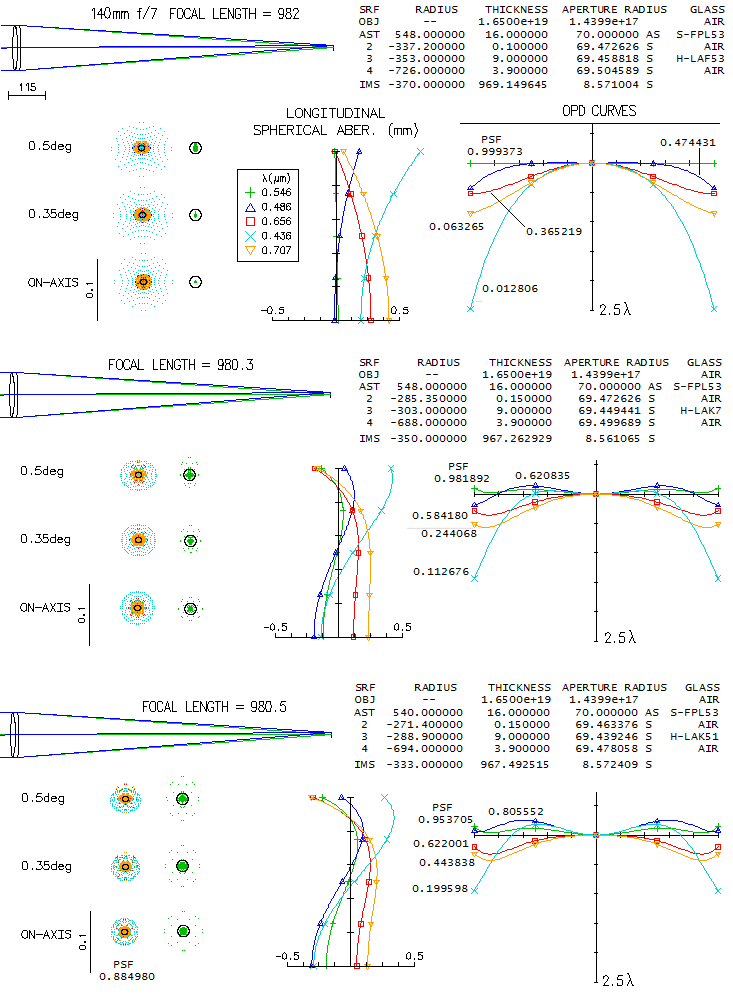
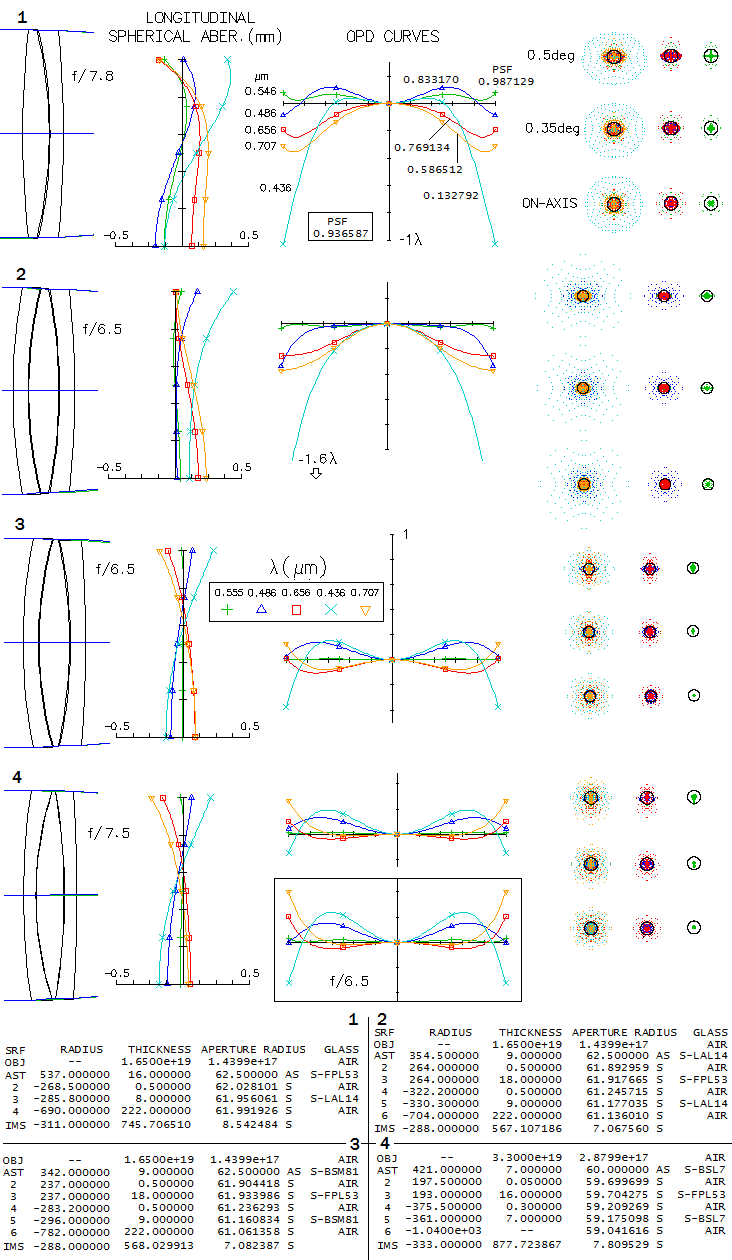
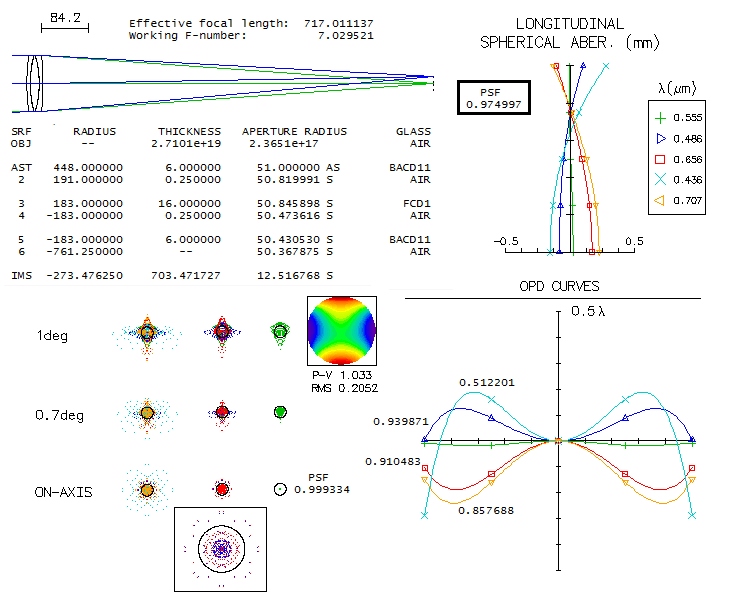
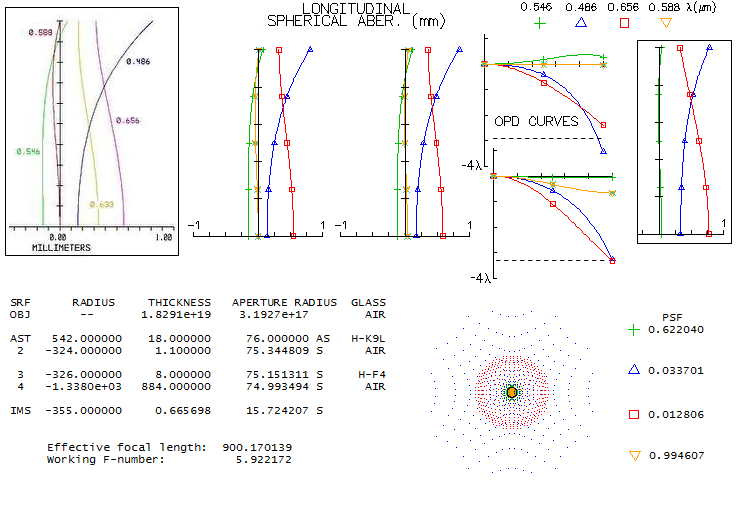
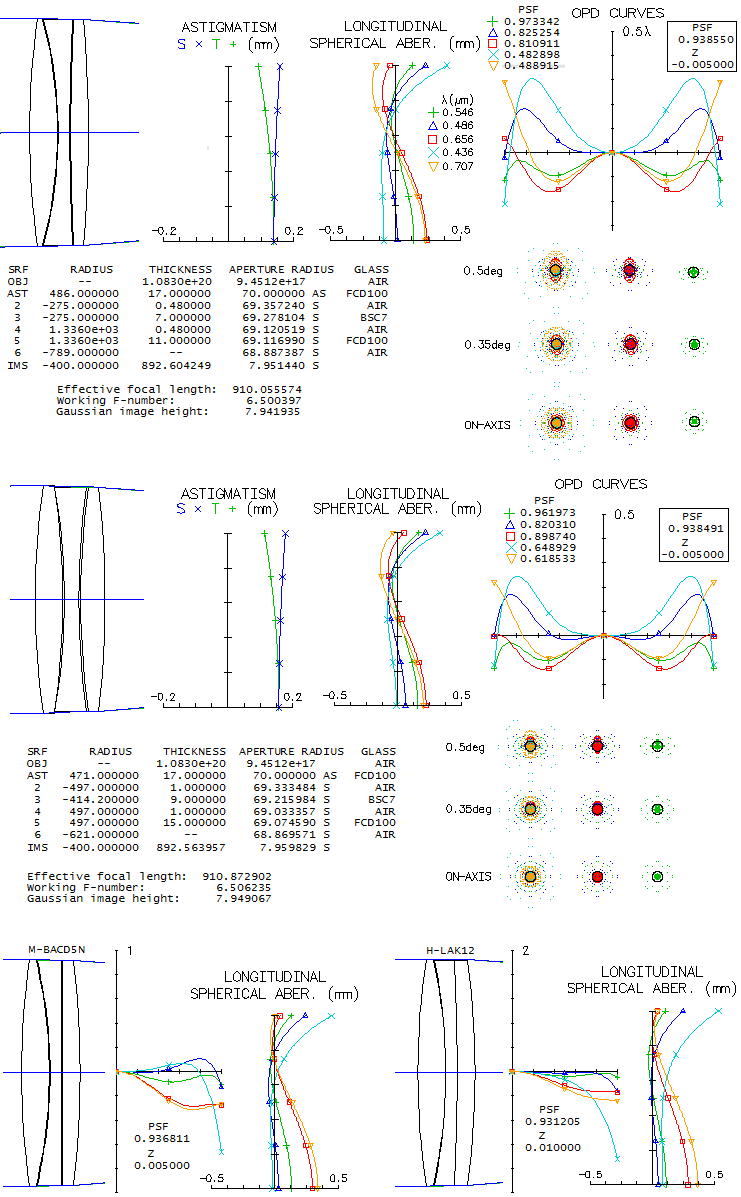
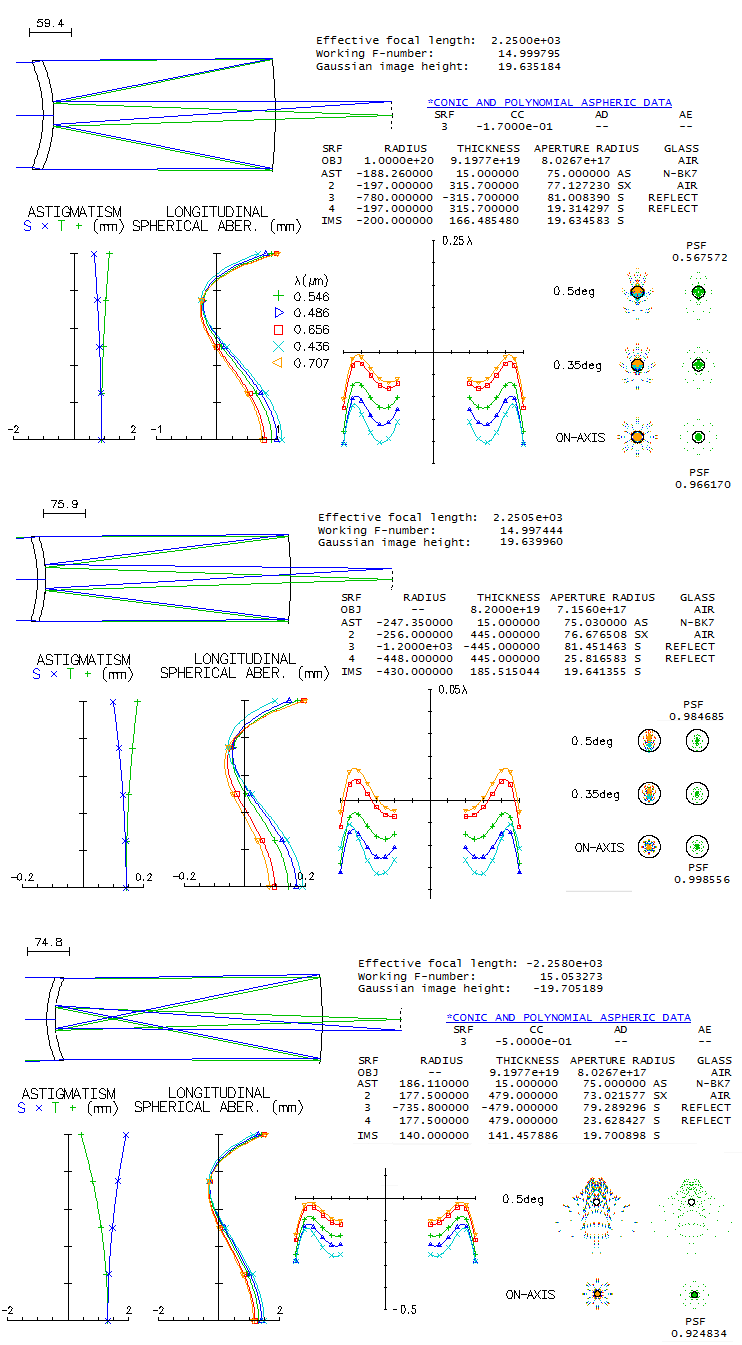
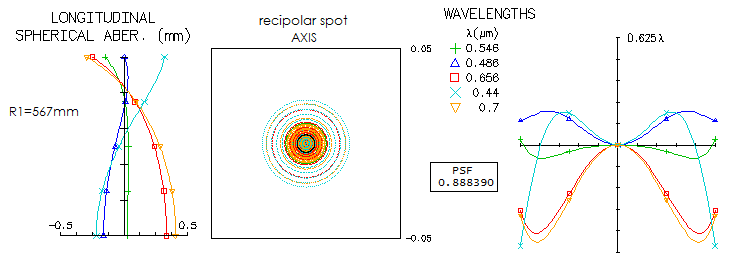
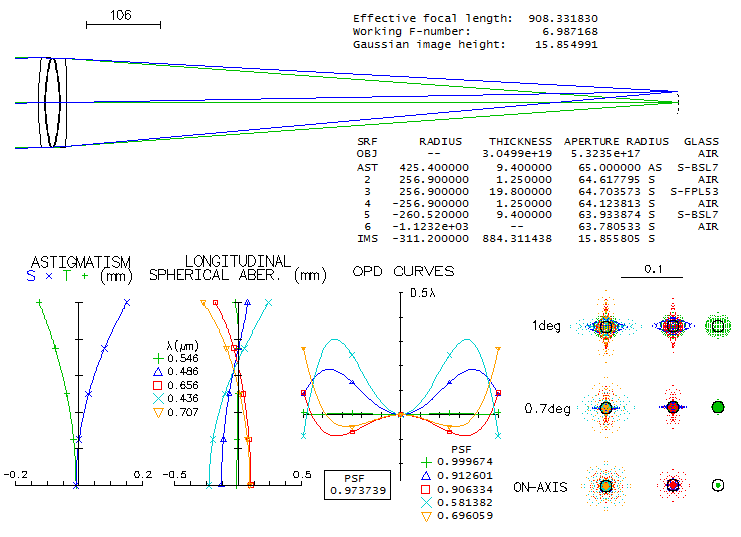
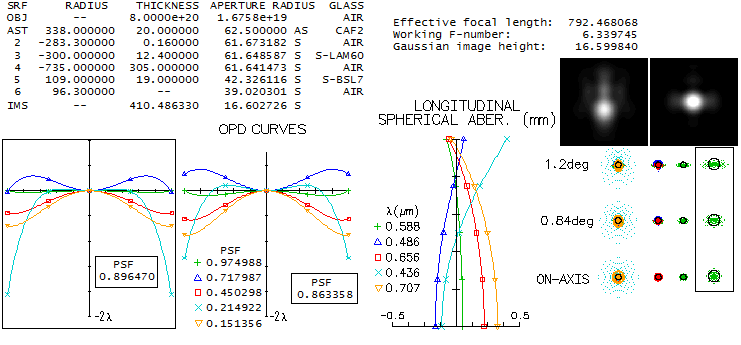
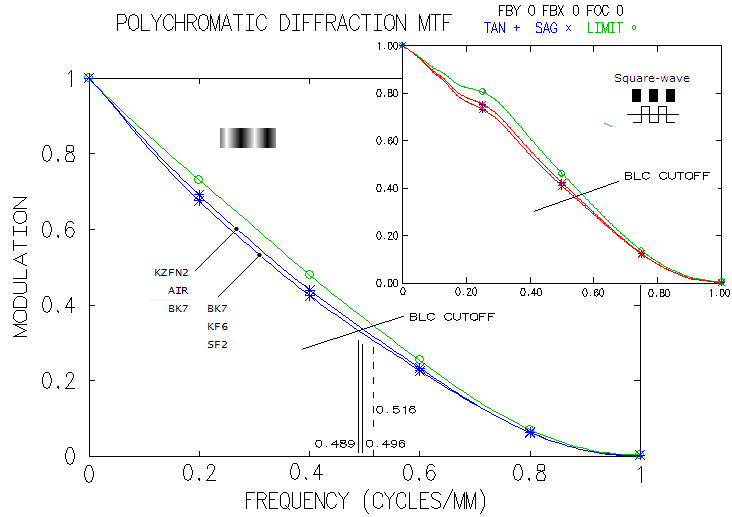
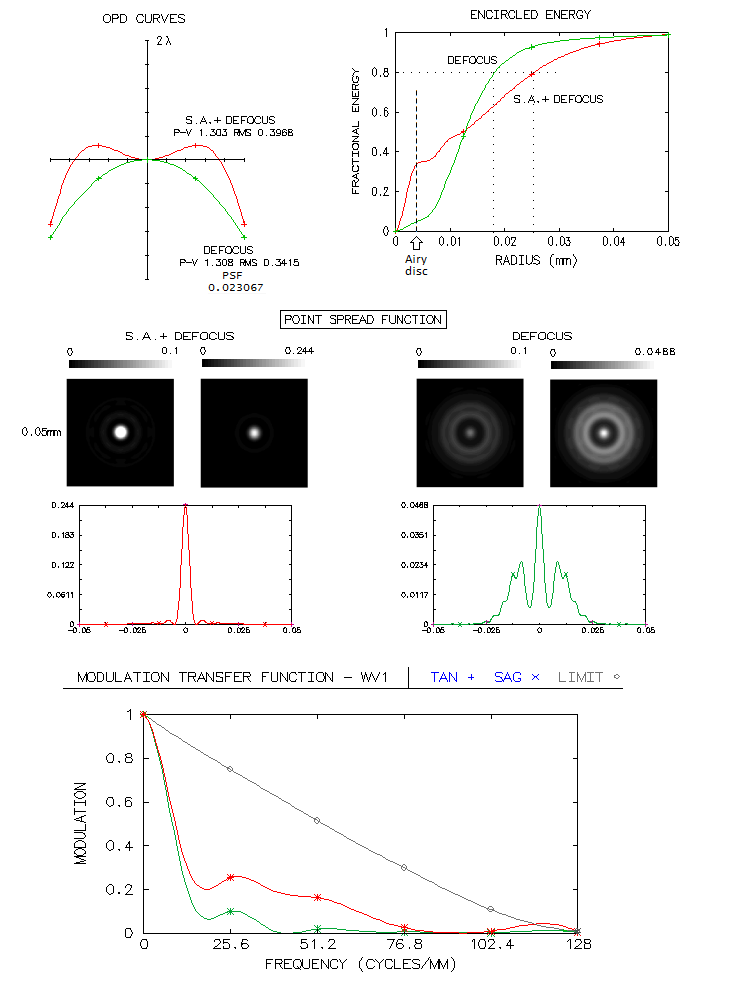
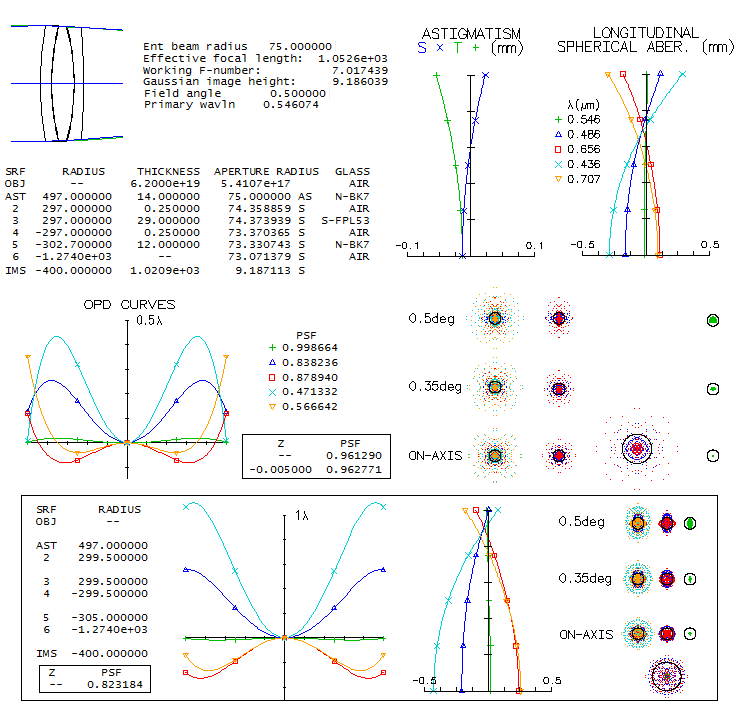
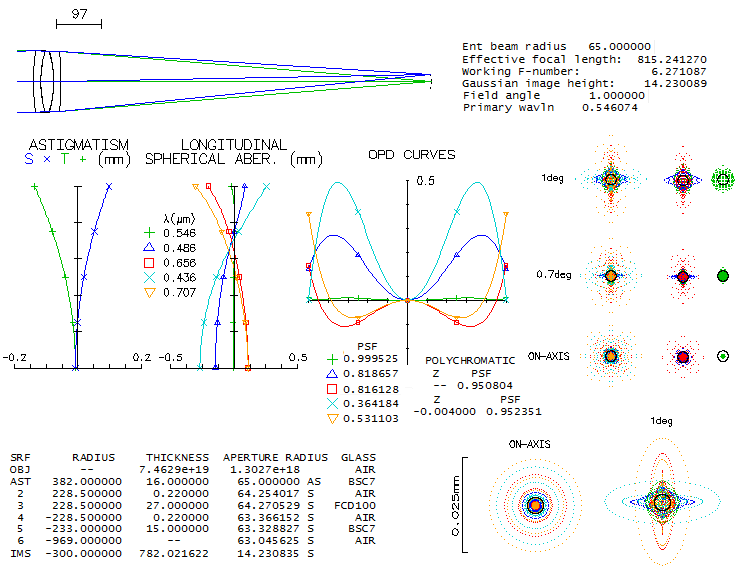
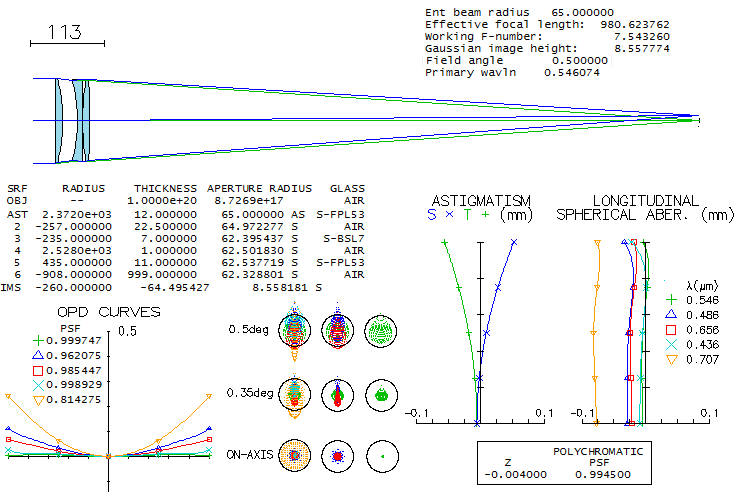
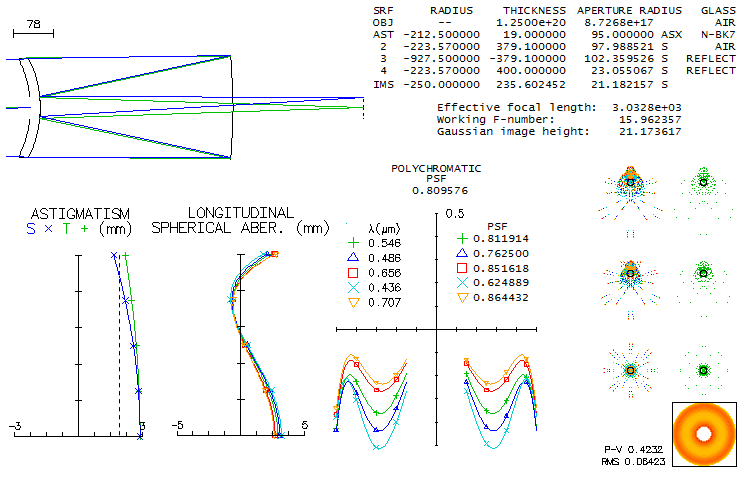
1 - 180mm f/7 apo refractorThis large apochromatic refractor, offered by several reputable manufacturers, comes in two main flavors: either with air-spaced, or oiled triplet objective. Also, it uses either Ohara FPL55 or fluorite as the extra-low dispersion element. When it comes to the air-spaced variety with FPL55, there's little doubt that the mating element is Ohara BSL7 glass, equvalent of the Schott BK7 crown. There is simply no better, cheaper and higher quality match available. Below is raytrace output for this combination (spherical aberration is minimized by altering the 5th radius, but it could be also done by altering one interspace, while keeping all inner radii equal; it would reqire 6.5mm wide second interspace, with no significant difference in the performance level).
With the Strehl of 0.35 and 0.65 in the violet g- and deep red r-line, 0.82 and 0.87 in the F and C, and 0.999+ in the e-line, it can be considered a "true apo" (just short in the g-line, but more than compensated for it with the excess of contrast-preserving energy in the red). It s confirmed by its 0.95+ photopic polychromatic Strehl. Expectedly, the Strehl is somewhat lower on both, CCD and mesopic sensitvity scale. The latter is approximated from experimental results, not the mere numerical average between photopic and scotopic that officially goes as "mesopic sensitivity". This vision mode is more representative for the night time observing, which implies that we need a higher than 0.95 photopic Strehl for the true "sensibly perfect" correction under such conditions. This combination can't be used for oiled triplet without aspherizing, but it is not a plausible option since wouldn't result in a performance gain. Longitudinal astigmatism of 0.37mm at 1-degree off axis implies 0.00094mm P-V wavefront error (from 0.37 divided by 8F2, same as for defocus).
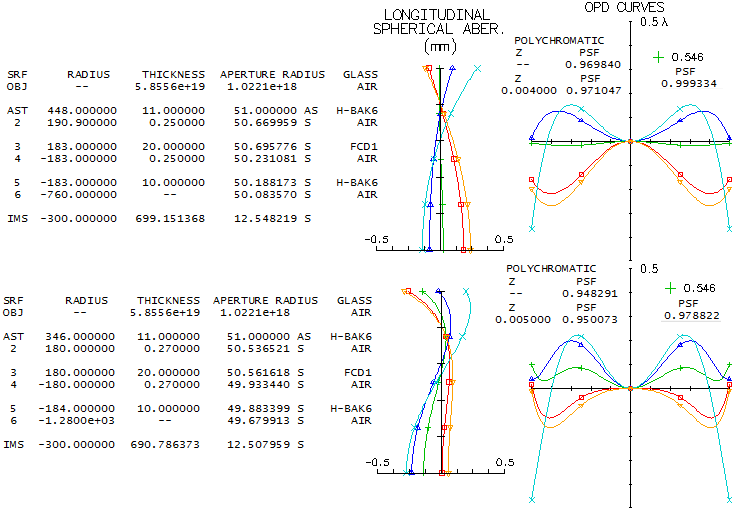
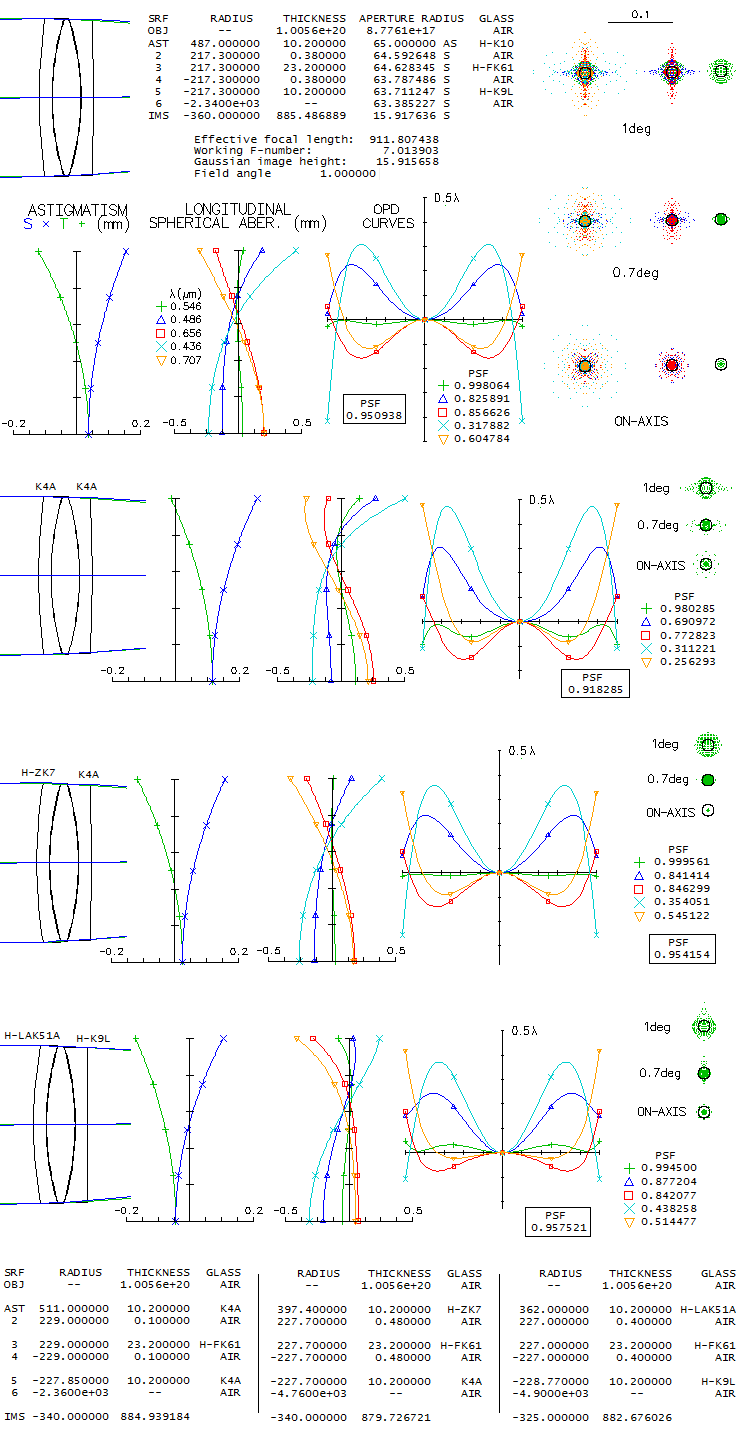
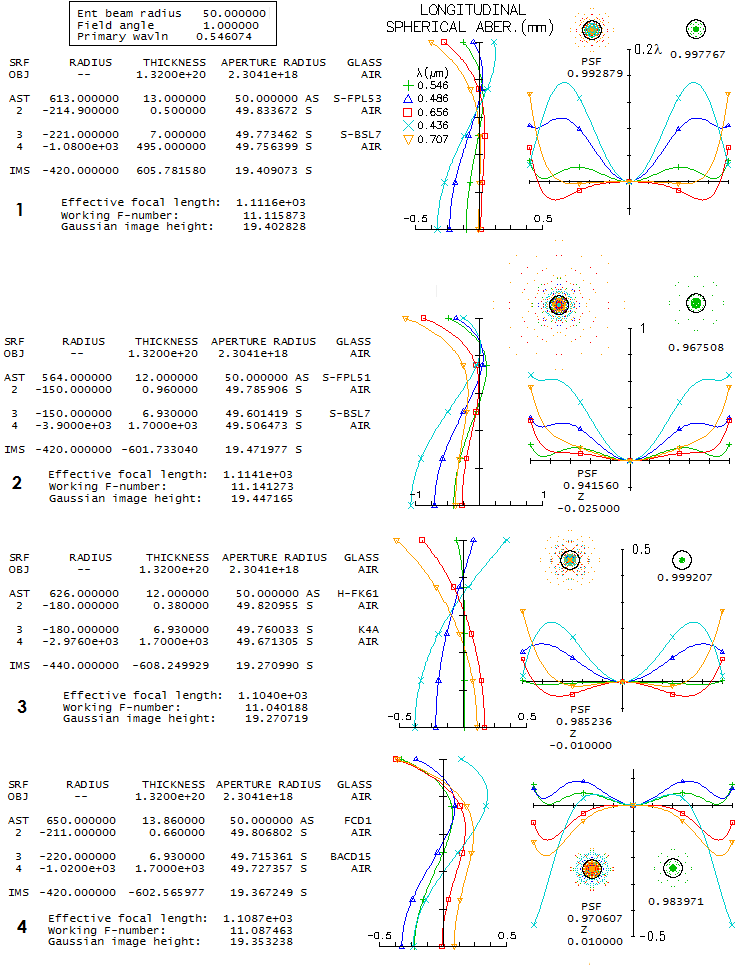
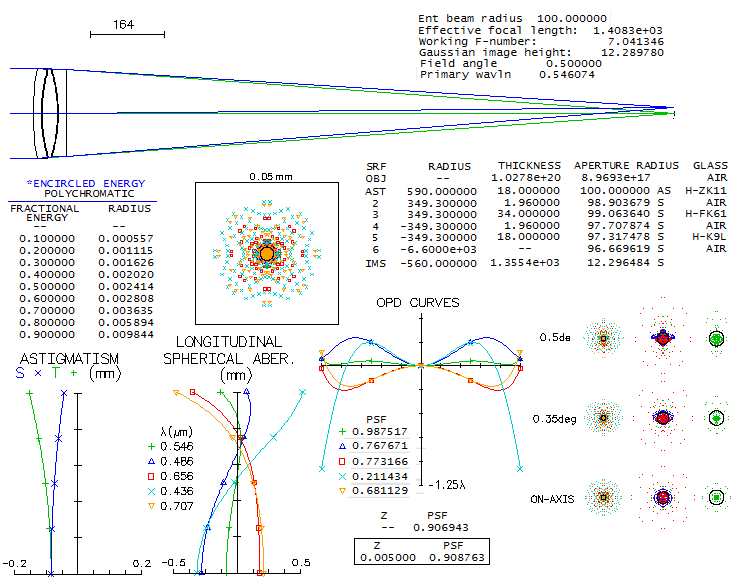
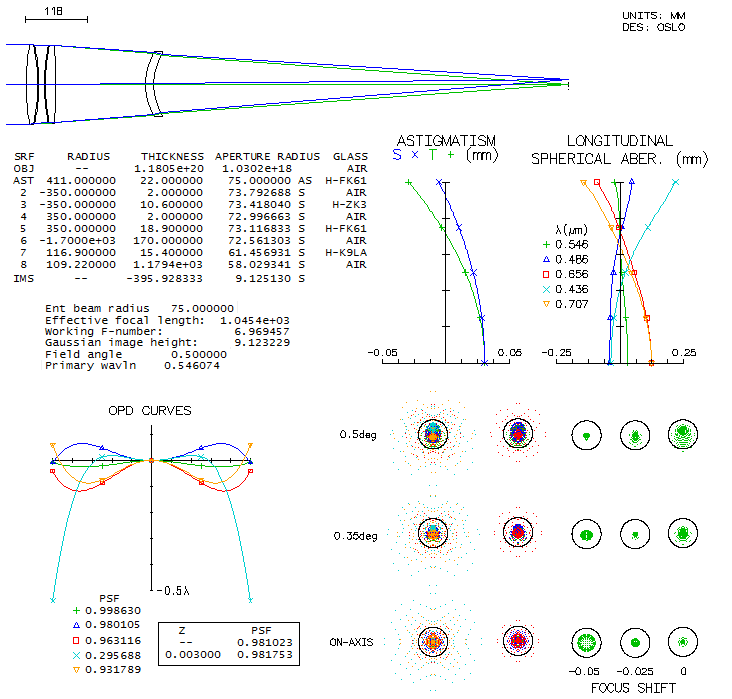
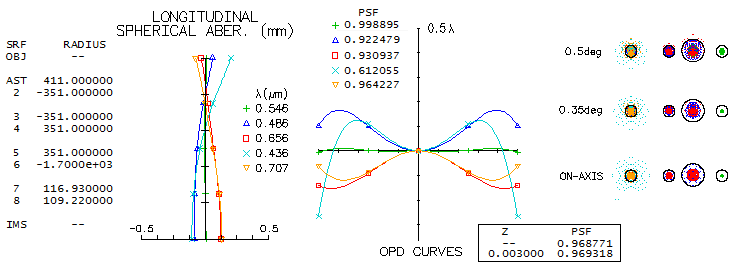
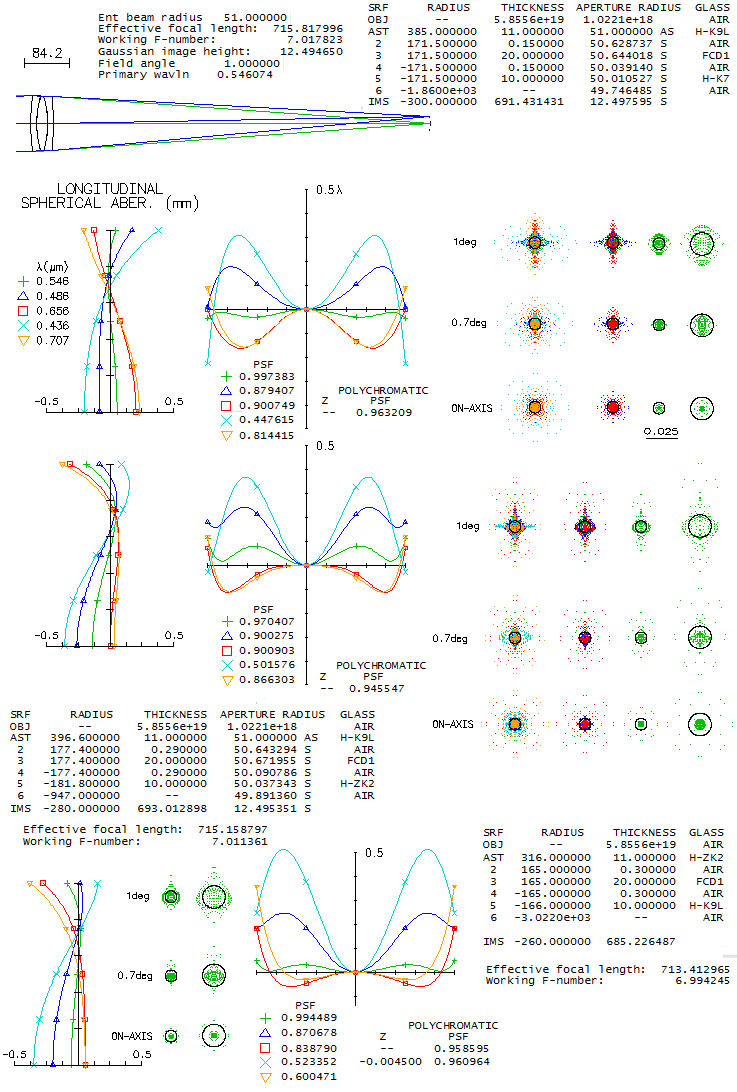
2 - 180mm f/7 fluorite apo refractorDoes fluorite guarantee superior performance? Another contender in the same aperture and focal ratio as the above lens is the TEC's fluorite triplet apo. While the only information available on this lens' design is that it uses fluorite as the middle element, all one can do is look at the available mating glasses and see what is the best that comes out. After trying a good number of combinations with matching glasses according to both, PF,e (for the F/C correction) and Pg,F (for the violet), one of the best was a combination with two glasses that have similar, but opposite in sign deviation from the ideal match: BK7 and K10. Its design parameters are shown below (top).
Performance level of this fluorite triplet is practically identical to that of the above FPL55 triplet, with the latter having only a slightly higher polychromatic (photopic) Strehl. It is, of course, possible that fluorite triplet design could be better than this one, but such glass combination is not readily apparent - and the same applies to the FPL55 triplet. Nearly identical correction-wise triplet can be put together using Chinese (CDGM) glasses, H-K9L (N-BK7 near-equivalent) in front, and H-K7 (it is somewhat different than BK10, but has near-offsetting index-to-dispersion differentials). Both designs could be probably pushed just over 0.95 Strehl, but that, of course, wouldn't produce noticeable improvement. It comes to what is pretty much a common knowledge, and it is that there is nothing magical about fluorite itself vs. other extra low dispersion glasses. In the end, it is the design and fabrication quality what decides how well a lens will perform.
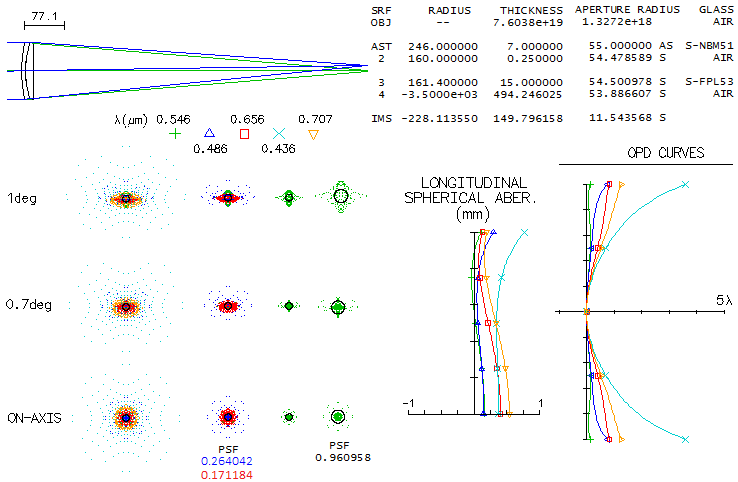
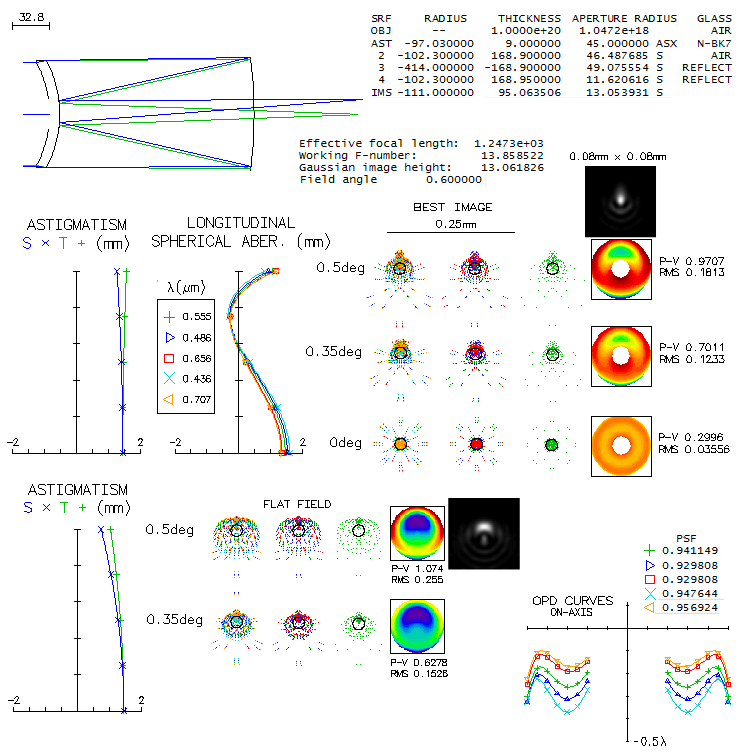
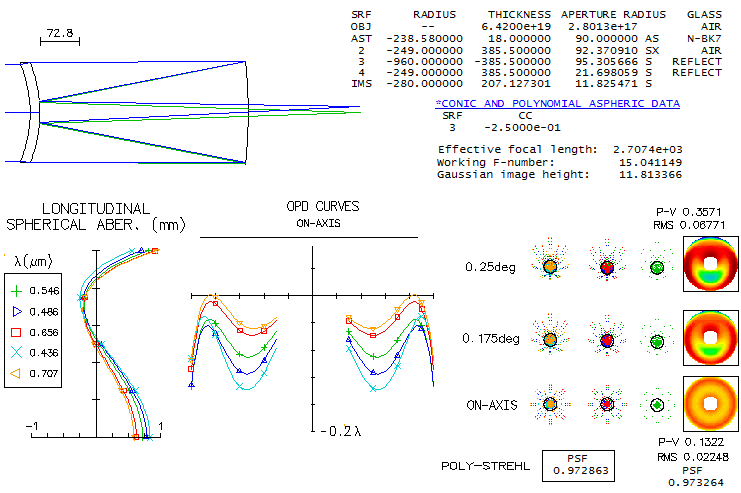
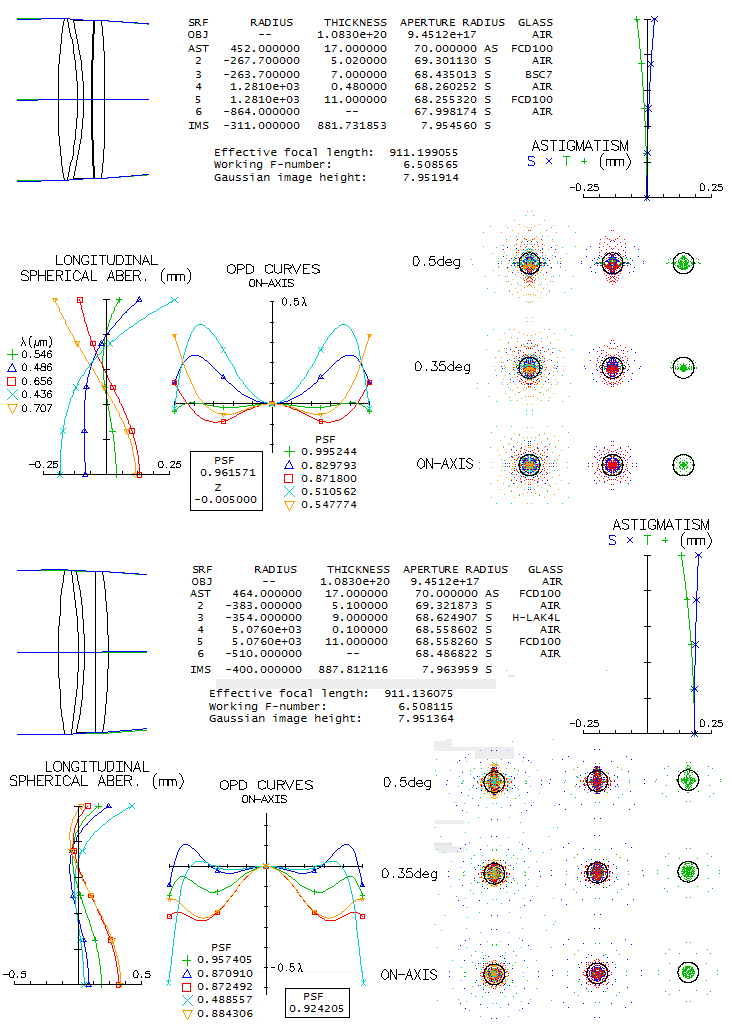
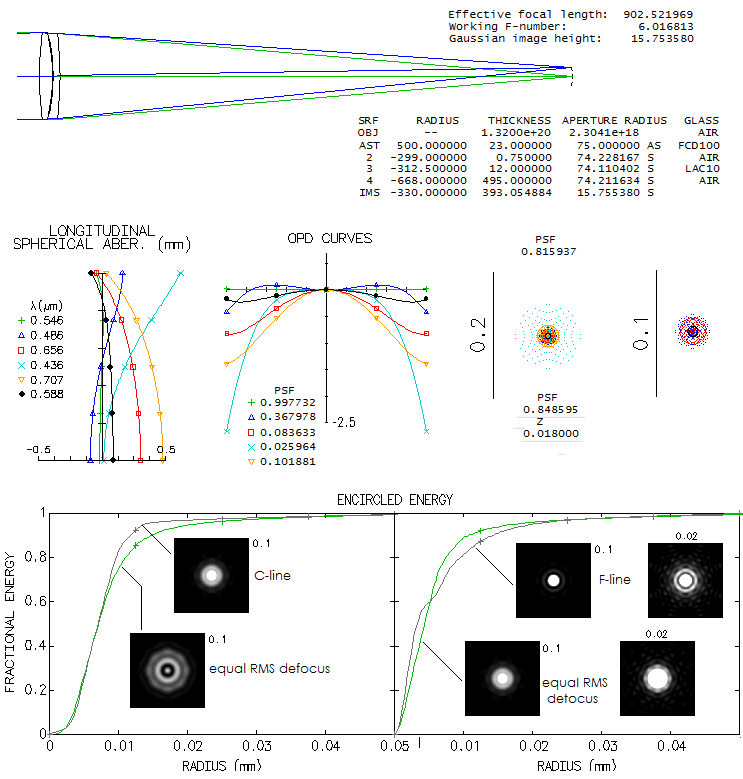
3 - Takahashi Mewlon 210Takahashi's Dall Kirkham reflector comes in four sizes: 180mm, 210mm, 250mm and the 300mm big gun. It is often speculated how much of off axis coma they generate. Luckily, Takahashi gives design specifications for all three, which makes it easy to create the exact optical design. The four are very similar, having ~f/3 primary and 4x secondary magnification. Since the primary is enlarged (+10mm on the diameter) it is not clear whether the focal ratios given were calculated vs. effective aperture or the actual mirror diameter. It is assumed the latter, but it wouldn't make significant difference if it is the former. The reason for enlarged primary is the displaced stop, placed at the primary's focus. It has no appreciable effect on coma, but reverses the sign of astigmatism, reducing field curvature nearly in half. Here's the raytrace for one of the smaller Mewlons, 210mm f/2.9/11.5 Dall-Kirkham system. Diffraction limited field, limited by coma, is 0.06 degrees radius if measured by the RMS wavefront error (0.0745 wave, for 546nm wavelength), and 0.68 degrees according to the P-V wavefront error (0.42 wave).
OSLO is inconsistent here, since the P-V/RMS ratio for primary coma is 320.5 (astigmatism is negligibly small in comparison this close to axis, and has no appreciable effect on the wavefront error). Taking 0.06 degrees, i.e. 2.5mm off axis, as the diffraction limited field radius, implies that its linear field is comparable to that of a f/6.1 paraboloid (from F=[h/48W]1/3, where h is the off-axis height, and W is the P-V wavefront error - taken as 0.42 wave - both in the same units). Of course, the corresponding angular field is proportionally smaller in the Mewlon. Also, it has proportionally larger image scale, which means that the linear diffraction image of the aberration is nearly twice larger. No effect on visual observation, since the objective's magnification is a part of total magnification (objective x eyepiece), but results in better sampling with any given CCD chip. Field curvature (R=-600mm) is mild, with no effect on visual observation. At 0.25° off, defocus vs. field center is 0.1mm, which corresponds to 1 diopter of accommodation (infinity to 1m object distance). Diffraction image for flat and best field (bottom) are virtually identical, coma being fairly insensitive to defocus, more so to as little of it (a bit more than 1/6 wave P-V). The system has 32% linear central obstruction diameter.
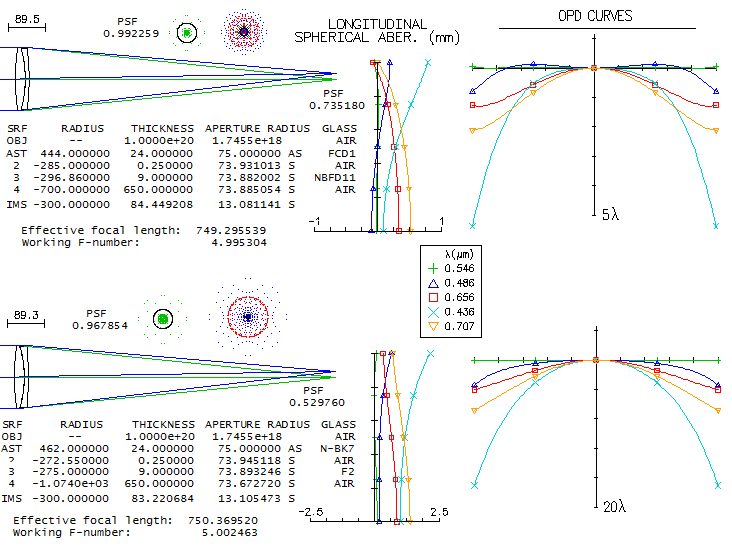
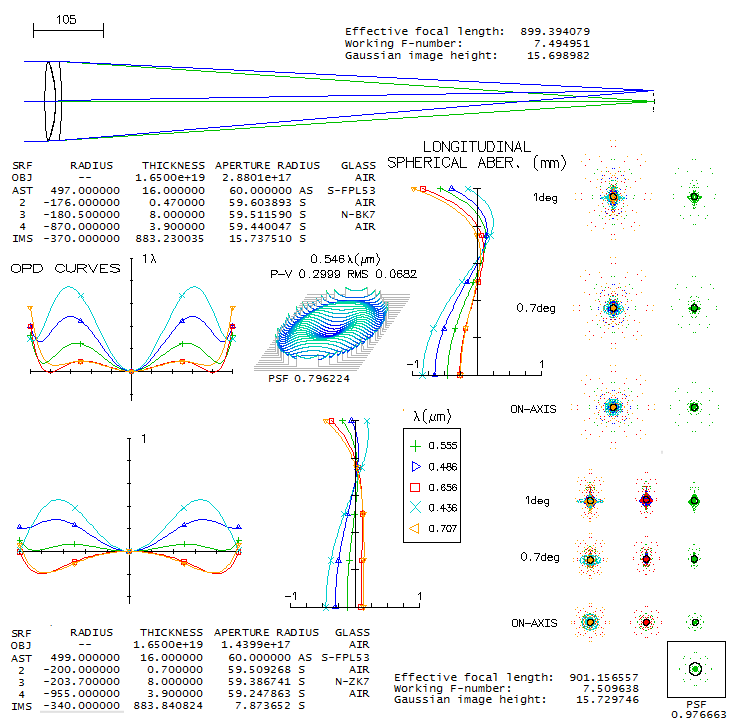
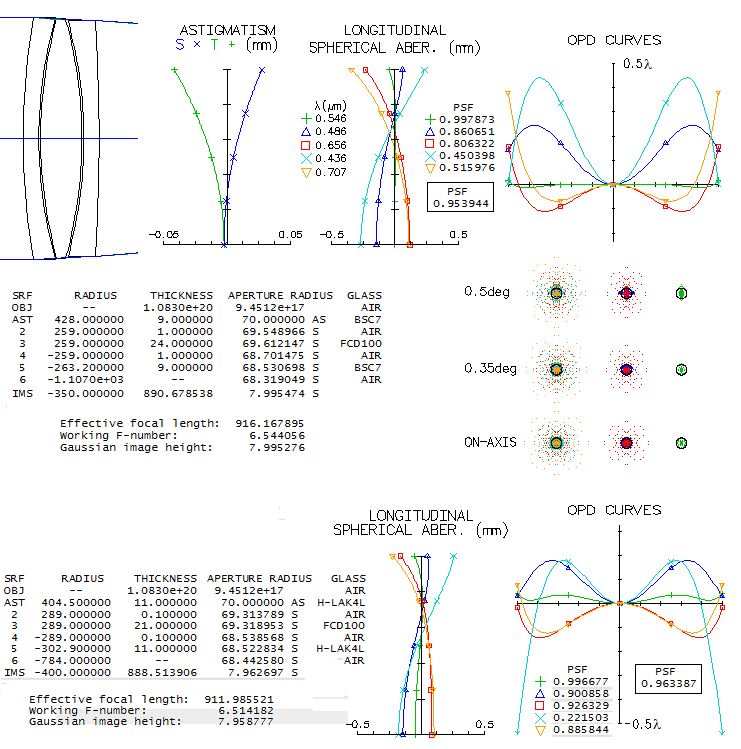
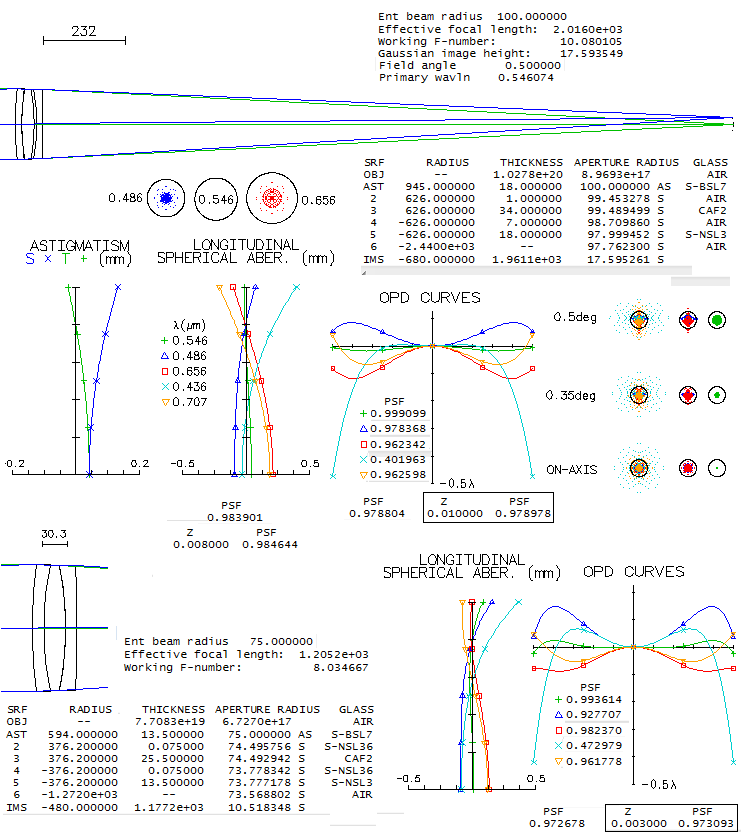
4 - AP 10" f/14.6 Maksutov-CassegrainOne of the cult telescopes in the amateurs' circles, the Astro-Physics' take on the Gregory-Maksutov design, never had its optics specs published, but since they are determined by the system parameters, it is possible to reconstruct them in the way that there is no appreciable difference in the performance level vs. the actual design. The purpose of aspherizing the primary is to remove the residual coma, with the extra benefit of somewhat relaxing corrector's radii, hence reducing the higher-order spherical aberration residual as well. The limit to aspherization is set by the coma introduced by it. If it is chosen to eliminate coma, with the standard corrector thickness of 1/10 the aperture diameter, it results in a design below.
The central line is just short of 0.95 Strehl (0.947 without its 23.6% central obstruction, 0.958 with it dialed in, due to it taking out the central wavefront deformation), and it is the main reason why the polychromatic Strehl is also below 0.95 (around 0.94 when unobstructed, which implies that the Strehl degradation factor due to the chromatism is only ~0.99). There are only two practical ways to somewhat improve the central line correction: one is with a thicker meniscus, and the other with more strongly aspherized primary. With 32mm thick meniscus, the central line's Strehl increases to 0.966 (0.971 with the obstruction), with a slightly larger (minimum size) secondary, and nearly 2" longer back focus. With the primary conic increased to -0.23 (at which coma at 0.25 degree off axis reaches diffraction limit - shown below ray spot plots - and design still could be called "coma free" in practical sense) the Strehl increases to 0.956 (0.962 with the obstruction). With both, thickness and conic increase, the central line's Strehl goes to 0.975. A 3% increase in the contrast averaged over MTF frequencies - which is what the Strehl value represents - is hardly noticeable at all. So the actual design may, and may not have these enhancements (with Roland's drive for perfection, it is more likely than not). Much more of a factor is seeing: even as good as 1 arcsec would lower the average Strehl of a perfect 10" aperture down to about 0.5 (D/r0~1.8). Yet, such 10" aperture still can deliver stunning views. An interesting detail is the star test. These instruments with the balanced 4th and 6th order spherical show more asymmetry in out of focus images than the standard, 4th order spherical aberration alone. It was pointed out more than once by those manufacturing such telescopes (including Roland) that a highly corrected telescope of this type will still show noticeably different in- and out of focus images. Can we trust them, considering conflict of interest? The bottom row shows OSLO simulations for the design in question with 0.97 central line Strehl (the one with thicker meniscus).
5 - ARIES' original 10" Maksutov-Cassegrain (?)Seems that quit a few amateurs believe that larger MC telescopes - and 10" would belong to that category - have to be aspherized in order to be well corrected. That, however, holds true only if the primary is kept at f/3, or so. Allowing for somewhat slower primary relaxes the required corrector radii, making possible to have significantly larger all-spherical systems well corrected. More so, such systems can be also coma-free. Commercially-made MC that fits the requirement of a slower primary is the original Aries' 10" f/13.5 telescope from the 1990's. While I'm not aware of the official prescription, a design can be made to illustrate its performance level. It will be a f/4/14.5 system with separated secondary mirror.
Correction level is stunning: the central line Strehl is 0.99+, and so are the ratios in F and C (needless to say, the polychromatic Strehl too). Field curvature is mild, and the minimum obstruction size is 27% by diameter. Needed optical tube is longer, but not excessively long. Angular field that fits 2-inch barrel is nearly 3/4 of a degree in diameter. The system could be easily rescaled to fit the original Aries, without appreciable change in the performance level.
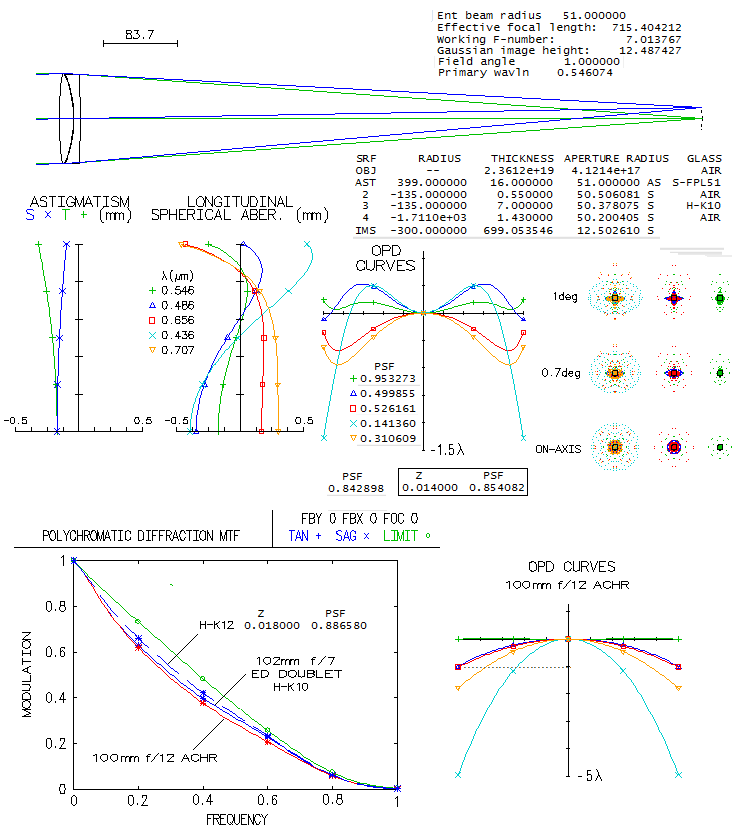
6 - TAKAHASHI TSA 102 f/8 apo tripletOne in the series of exquisite Takahashi refractors, the TSA 102 had its optical design revealed during its marketing campaign. Here's how it raytraces.
On the design level, there is no chromatism to speak about. Polychromatic Strehl in the 430-670nm range comes to 0.992, while in the optimized wawelength it is 0.9998. The polychromatic MTF is practically coinciding with that of a perfect aperture. There is some residual coma. While it is visually unnoticeable, it does make point image asymmetrical, and enlarges the 80% energy circle at 1-degree off axis by nearly 1/3. It is easily removed by adjusting the outer radii (R1=344mm, R6=-944mm, with R3=179.5mm and the second gap increased to 0.45mm to minimize spherical aberration), but the reason it's there, as graph on the Tak site shows, is that it gives a coma-free image with its dedicated focal reducer.
Just how good this triplet is illustrates the fact that its polychromatic
Strehl is still as high as 0.962 even when scaled down to f/6, although
the tolerances are much tighter. That is one of the Takahashi's secrets:
they don't push the envelope, making it possible to execute design to
near (practical) perfection.
7 - Cheap ED doublets: how good they are?Cheap 4" ED doublets, like Svbony Sv503 and Astro-Tech AT102ED, use lower-grade ED glass - FPL51 and the optically near identical FK61, respectively. Both come at the fairly fast f/7 focal ratio. Mating material is not mentioned, which leaves a wide range of possibilities, from ordinary crowns, like Schott K7, K10 and alike, to somewhat obscured N-KZFS2, and to acrylic-like optical plastics.
Finally, optical plastic going under ZC1 in OSLO catalog has similar properties to acrylic (which itself produces not negligible secondary spectrum with these ED glasses), is probably a kind of cyclic olefin polymer (COP), known as ZEONEX. It allows for a very similar correction level as K7 but - it should be safe to assume - at a lower cost.
With their 0.86 polychromatic Strehl, i.e. overall contrast level, the
combinations with K7 and ZC1 would be comparable to a 100mm f/20 achromat.
Factors that boost achromats poly-Strehl are its better design correction limit
in the optimized wavelength, as well as the non-optimized wavelengths error increasing
with the square of index differential vs. optimized wavelength, as opposed to the
near-proportional increase with spherochromatism - according to the nominal error in F and C,
the two ED lenses would be comparable to the f/25 achromat. However, with respect
to the apparent chromatic error, they are significantly better, due to their
color foci being much closer together, with most of the nominal chromatic error
coming not from defocus, but from spherochromatism, which lowers contrast just
the same, but is much less colorful.
Interesting detail is that despite its lower P-V and RMS wavefront error
in the violet h-line, the objective with a plastic element has significantly lower
Strehl value for this line than the K7 lens. At the same time, its radius of 80% encircled energy
is significantly smaller - 0.0224mm vs. 0.0276mm for the lens with K7 element.
It shows that the Strehl value at large wavefront errors - roughly over 0.15 wave RMS -
becomes unreliable metric for the level of optical quality, as the central intensity
becomes less representative of the overall energy distribution.
8 - Questar 3.5" StandardNo other commercial telescope had such an aura, and cult following as this small 89mm f/14.4 Maksutov-Cassegrain telescope in production since the 1950s, and in this form from 1960s. Going at 2-3 times the price of a quality apo triplet of the same aperture, how good it really is optically? There are all kinds of reports, most of them impressive, from 1/10 wave P-V, or better, tested, including an owner reporting as good as 0.987 Strehl - better than 1/16 wave P-V of primary spherical aberration - test result from "Company 7". Questar Corporation on its side states that the telescope has "no coma, astigmatism, or spherical aberrations". No wonder more than a few people believes that this little telescope actually performs above the limits set by the laws of physics. Since there is no secrets on how the Maksutov-Cassegrain works, all needed for determining the performance level is a single number, the mirror focal length (the size of central obstruction is published). Knowing the final focal ratio determines mirror-to-corrector separation, since for a given corrector thickness there's only a single set of its radii that will correct both, spherical aberration and longitudinal chromatism. Since it is so-called "spot-Maksutov", with the secondary being an aliminized spot on the rear corrector radius (since 1960s), the constraints imposed in this configuration make possible deviations from the actual arrangement negligible. In absence of the mirror focal length, even the mirror-corrector separation will do, since the known final focal ratio determines the width of the axial cone on the rear corrector's side, and with that the effective focal length of the primary (for the light refracted by the corrector). Variations in the corrector thickness, within the standard range, have only minor effect. This side cross section provides all information needed to reconstruct the Questar system. The dimensions correspond well to the actual O.T.A. (back focal length could be up to 20mm, or so, longer). The final system based on these values is shown below, with spherical (left) and aspherized primary.
It is not known whether the primary is spherical or aspherized. According to the information available Questars were all-spherical in the 1954-57 period, and had the aluminized spot on the first radius up to 1978. Having aliminized spot on the first radius changes the performance level in this configuration only slightly. Corrector radii need to be somewhat stronger (-87.5/-92.6mm), and the secondary area on the front surface would need to have yet stronger radius (-82.1mm) in order to produce f/14.3 system. Back focal length would be insufficient, which means that either: (1) the mirror would have to be placed a bit closer to the meniscus (~1mm, in which case the system f/ratio would be ~f/15) with the secondary radius of ~-83mm, or (2) only the secondary radius would be made slightly stronger (-81mm) producing ~f/16 system. The system can be coma-free only with the primary aspherized (all-spherical arrangement has linear coma-limited field equal to an f/7.4 parabola), which would imply aspherization, but how serious we can take that claim, standing next to "no astigmatism and spherical aberrations" too (Questar Standard 3.5" Telescope Specification Sheet)? Taking that "no" means "no perceptible", spherical aberration in this sistem can be brought down to that level only by putting higher order aspherics on the meniscus, or primary. Putting higher-order aspherics on the meniscus, or primary, doesn't affect the system coma, so the primary still needs to be aspherized to make it coma-free. Starting with the bare-bone, all-spherical version above, keeping the meniscus-to-mirror separation, central obstruction, and final focal ratio unchanged, will take a look of three possible scenarios of putting higher-order aspherics on: (A) front corrector surface, with primary, i.e. 4th order spherical reduced to near-zero by altering corrector radii, (B) also on the front corrector surface but with the 4th order spherical reduced by putting 4th order aspheric on the corrector, and (C) by putting higher-order aspherics on the primary (putting 4th order aspheric on it generates lower-order coma of the same sign as the system's higher-order coma, making it impossible to correct coma). Specifications, along with the performance level for all three is given below (note that secondary radius in the system B should be equal to the rear corrector radius, which causes imperceptible change in correction, but the primary r.o.c. needs to be increased to 399 to maintain the final focal ratio; for minimizing the aberration, AD needs to be changed to 2.02e-9 and AE to 3.33e-13, with the final output nearly identical to the one shown).
There is no way to know which - if any - of the three was used, but putting higher-order aspherics and conic onto the primary (arrangement C) seems to be the easiest, hence most likely. Omitting the 8th order term would put design limit to 1/14 wave P-V, and would require adding the 6th order curve - 0.000222mm, or 0.4 wave at the edge, but since negative in sign would require that much deeper center - to the conic curve. Longitudinal astigmatism at 0.5 degree off axis is nearly 0.3mm, which gives 0.00018mm P-V wavefront error, or 0.33 wave for 0.00055mm wavelength (from 0.3/8F^2, same as for defocus). That is still below the "diffraction limited" 0.37 wave P-V for primary astigmatism. The MTF graph published by Questar Corporation (same source) should help, but it doesn't. As picture below shows, it doesn't match neither MTF graph for balanced primary spherical (middle), in case they used it for expressing the error, nor MTF for the actual (balanced secondary spherical, right) aberration of the all-spherical arrangement (MTF for the arrangement with aspherized primary is much tighter for the design limit, and would become similar only if the actual units would have significantly larger axial error), let alone the arrangements with higher-order aspherics (MTF not shown, practically coinciding with the limit). In the lower frequencies, the Questar's MTF plot is concave, while it should be flat to mildly convex; in the high frequencies there is a very pronounced - and quite unusual - contrast drop. In fact, if we'd assume the customary 5% minimum contrast needed by the eye for resolving a line pair at the limit, the typical Questar would have its limiting field resolution about 5% lower than the limit imposed by the aberration-free MTF (given by Questar).
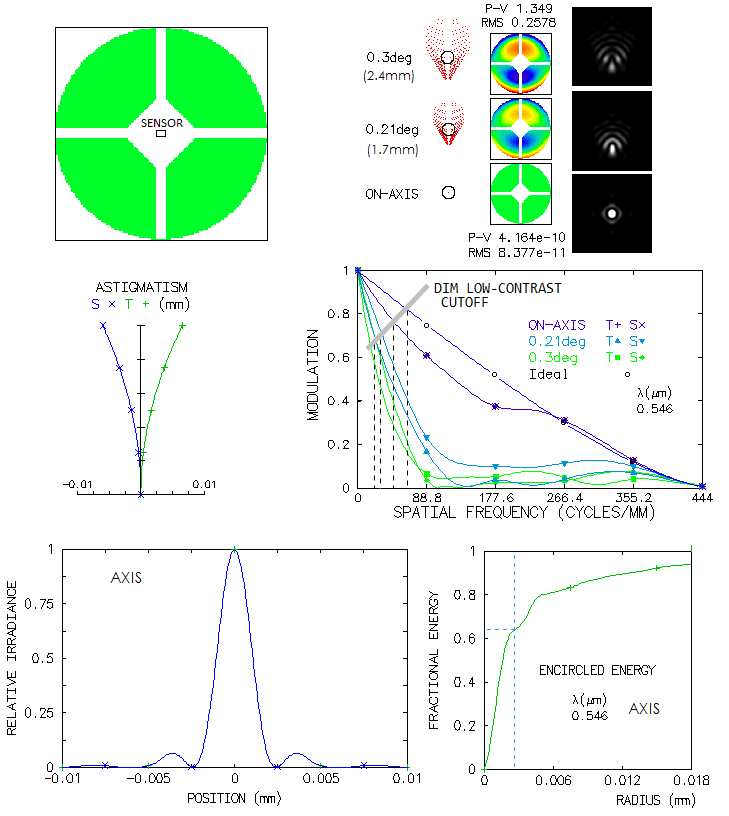
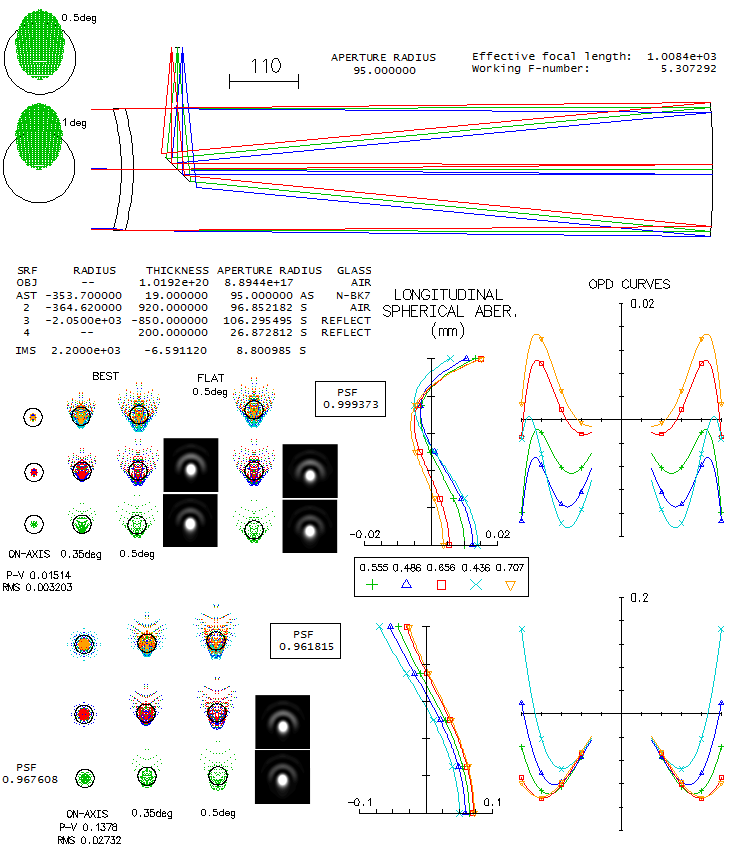
Summing it up, Questar's claim that its telescope has "no spherical aberrations" directly implies that it uses higher-order aspherics. This would raise its design limit to 0.9996 polychromatic Strehl (photopic, for the arrangement C above), from 0.916 with all-spherical arrangement, and 0.962 with ellipsoidal primary. The coma-free claim implies that the primary is ellipsoidal. As for the "no astigmatism" claim, it is not quite true. It is as low as 0.3 wave P-V at 0.5° off - which makes it visually unnoticeable - but it is present. This generally describes its design and, the fact is, its limit, in terms of polychromatic Strehl, is perfect 1. 9 - UniStellar eVscopeWould you pay $3000+ for a 4.5-inch Newtonian reflector? With a sophisticated goto mount, and 100,000X photon flux intensifier? Some people would and, judging on the published ratings, they are satisfied with what they've got for their money. The eVscope comes in two models, one w/o eyepiece, intended to use your smart phone display, and the other with a special eyepiece, connected to the photon-intensifying sensor placed in the mirror's image plane. Both are intended primarily for deep sky objects observations at a low (50X) optical magnification and up to 400x (up to 150x recommended) digital magnification. Perhaps for that reason, combined with the fairly small field covered by the sensor, the mirror image is left uncorrected for coma and field curvature. How does that affect optical quality? Picture below illustrates main properties of the image supplied by a perfect 4.5-inch paraboloid, including the effect of a fairly massive obstruction by the spider vanes and sensor housing. The sensor comes in two sizes, 27'x37' in the model w/o eyepiece, and 34'x47' w/eyepiece, with the limiting resolution - determined by sensor properties - of 1.72 and 1.33 arc seconds, respectively (theoretical limit for the aperture is just about 1 arc second). Considering the intended purpose, the inferior limiting resolution is of no consequence since - as the MTF graph shows - cutoff frequencies for deep sky objects are several times the ultimate (high-contrast) cutoff at best.
The 0.3° field radius is just a tad smaller than the longer sensor half-size, in the model w/o eyepiece, and the 0.2° field radius a tad larger than the short half-side, which means that sensor corners have somewhat more coma, and so does the larger sensor, in proportion to its size. The spots are given for the best image surface (R=480mm) but it is practically unchanged on flat field, due to the small field size and the relative insensitivity of coma to defocus. At about 0.01mm longitudinally, astigmatism is negligible (P-V=0.01/8F2). However, as MTF graph shows, the loss in limiting resolution is significant even at the relatively low frequencies resolvable with deep sky objects, even if the contrast loss is quite moderate. At 50x magnification, sagittal coma at 0.3° is nearly 5 arc minutes, large enough for its shape to be recognized by the eye. On axis, encircled energy is ~0.64, comparable to the effect of a 0.45D (45% the aperture) central obstruction w/o vanes. While this may be acceptable considering the purpose, image quality would still benefit from a coma corrector - more so in the model with a larger sensor.
10 - APM 140mm f/7 SD Lanthanum confusionOn its site, APM states that this ED doublet uses Ohara FPL53 mated with the CDGM's H-LAF53 glass. However, this combination has too much of a residual secondary spectrum to fit into published Strehl-across-the-wavelengths graph for this refractor. As image below shows (top), the F (486nm) and C (656nm) lines are at, or near 1/2 wave P-V wavefront error, and their Strehl numbers fall significantly below 0.78 and 0.65 (approximately, since this line was cut out of the graph) respectively. The violet g-line is at 2.5 waves, comparable to a 100mm f/23 achromat.
Some time ago, on forum talk, Markus Ludes was cited as specifying for the mating element another Chinese Lanthanum glass, H-LAF7A. While coming closer to the published Strehl values, it is still falling short (middle). Glass that reproduces given F and C lines Strehl values, and also corresponds better to the published central line Strehl, is H-LAK51 (bottom). OSLO gives its cost as 3, in units of the BK7 cost, which also makes it more likely choice than H-LAF53 at 4.5 times the BK7 cost. The violet g-line error is still relatively large at 1.1 wave P-V, but this is comparable to a 100mm f/50 achromat, hence not very noticeable. Moreover, the scope description by some vendors uses the words "Lanthanum coatings" which, along with "new materials" indicates that a special kind of coating was used to cut out better part of the violet. Some materials, when doped with Lanthanum, can selectively absorb ultaviolet bands. For instance, LiNbO3 (Lithium niobate), doped with 5% Lanthanum, transmits only about 65% at 450nm, and less than 10% at 430nm, while transmitting over 90% of the longer wavelengths (undoped, it is near zero already at 450nm, but transmits only about 60% of the wavelengths over 500nm). With optimized transmission, light loss in the rest of wavelengths probably can be made negligible, with the absence of violet giving more abundance to the red hue - noticed in some reviews. The photopic polychromatic Strehl for the 430-670nm range comes to 0.89, which is about the level informally announced by Markus.
Note that polychromatic Strehl incorporates
all colors, including the optimized, green-yellow. Hence it would have been
better if the central line Strehl was better. If it was, say 0.99,
the corresponding poly-Strehl
would be 0.923, sensibly quite close to the "sensibly pefect" 0.95 (bear
in mind that it is photopic Strehl, with the sensitivity in both blue/violet
and red increasing significantly toward the more applicable field mode
for night-time observing,
mesopic, and the mesopic Strehl being correspondingly lower - this
applies to all chromatically imbalanced systems, but affects more the
blue/violet end, typically less well corected than the red). In other
words, the farther the central line Strehl is from perfect, the more
the off-color correction is better than the poly-Strehl indicates.
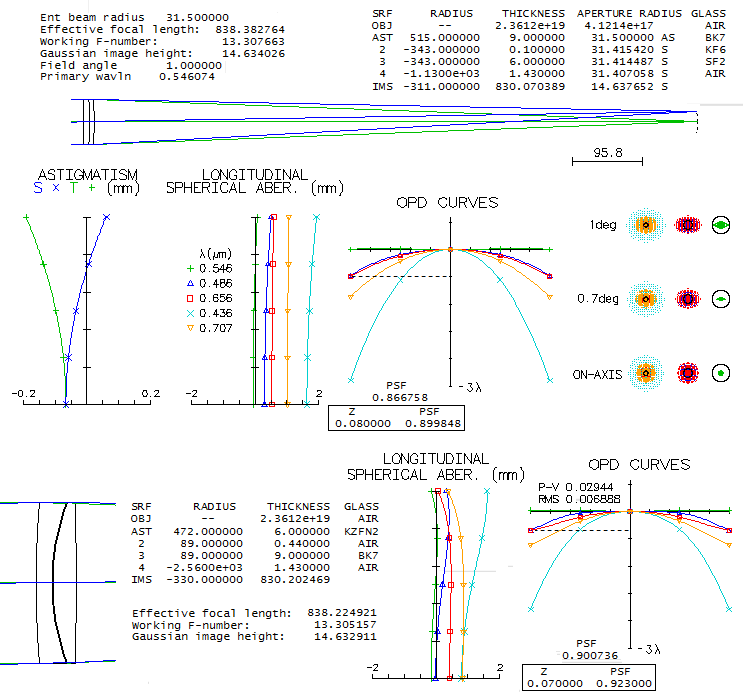
11 - 150mm f/5 ED doubletIs the TS-Optics 152mm f/5 ED doublet well corrected for chromatism? Those somewhat familiar with lens design know that ED doublets require significantly more strongly curved inner radii, hence with such a fast system will generate much more of higher orders of spherical aberration - secondary (6th order), tertiary (8th), and even 10th order is not negligible. This, in fact, eliminates all mating glasses that would bring all colors close to each other, since Abbe differential required to bring higher order spherical aberrations to acceptable level leaves only glasses higher on the RPD diagram than Hoya's FCD1 - the ED glass cited for this refractor - thus inevitably producing some secondary spectrum. Glasses suitable for the mating element are lanthnoids similar to the Schott's short flints with the lower Abbe number. Since the ED glass is from Hoya, it is more likely than not that the mating glass is from the same source. Hoya still lists some short-flint-like glasses, for instance E-ADF10 (Abnormal Dispersion Flint similar to Schott's KZFSN4). Somewhat better overall is another lanthanoid, NbFD11 (Niobium Flint, Dense, equivalent to Schott's N-LAF33, listed by OSLO at 4.4 times the BK7 cost). Image below shows performance level of this combination, compared to the standard BK7/F2 achromat.
The ED doublet does have significantly better correction, reflected in
the photopic polychromatic Strehl (note different scales for both, longitudinal
SA and OPD graphs). But how good it is? Well, the ~1 wave F/C average
puts it at the level of a 100mm f/12 achromat, while the 5.3 waves
in the violet g-line corresponds to f/10.6 achromat of the same aperture;
the red r-line is at the level of f/10.8, and the poly-Strehl at the f/10.2
level.
The violet can be tamed with lanthanum-doped coating, but it is not
known whether or not such was applied.
12-Omegon AP110/660 ED doubletProbably the fastest on record ED doublet for this aperture size raises question of how good its color correction really is. Since the two glasses are known, the answer is as simple as putting them together. The FPL53 positive element boosts confidence that it should be nearly as good as possible, but the mating element, S-NBM51, is what will determine the outcome. It is a near-equivalent of the Schott's N-KZFS4 "short flint", and the reason it's been selected is obvious: it is far right from FPL53 on the relative partial dispersion diagram (RPD), i.e. with a large Abbe number differential between them, which generally allows for more relaxed doublet's inner radii, hence also less of higher order spherical aberration. Also, short flints are generally better a match than lanthanum glasses, which is the only other group in this part of RPD diagram. Below is how this combination raytraces.
The LA plot shows some residual secondary spectrum, which was to expect considering that NBM51 to FPL53 RPD differential is not negligible. Most of the error in F and C lines comes from defocus (i.e. secondary spectrum): for instance, F line is 0.2 waves P-V at its best focus, and 0.75 waves at the best green focus. The design limit in the optimized line is 0.96 Strehl, which puts the best one could expect in the actual unit at ~0.95, or 1/8 wave P-V of spherical aberration equivalent. The weakest point is, as usual, the violet end: g-line error is over 3.5 waves P-V. This puts it at the level of a 100mm f/16 achromat, while the 0.8 wave averaged for the F and C lines correponds to a 100mm f/15 achromat. Considering it's 110mm aperture, it is roughly at the level of a f/17 achromat - except that the achromat should have a better central line correction. Is this the best possible mating glass for this configuration? No. There are very few choices for such a fast doublet altogether, but Schott's N-KZFS2 would do considerably better. It would have no secondary spectrum residual to speak of, F/C average anywhere from 1/4 wave P-V to 0.4 wave (the latter with minimized g-line error), and g-line error from 0.7 wave (when minimized) to 1.1 wave (with minimized F and C). The only reasons not to use this glass is that Ohara probably doesn't have near equivalent, and that it would require somewhat stronger inner radii, with somewhat tighter tolerances. Note that there is no significant difference in performance between arrangement with FPL53 in front, and in the back, but the latter seems to be having a bit better correction.
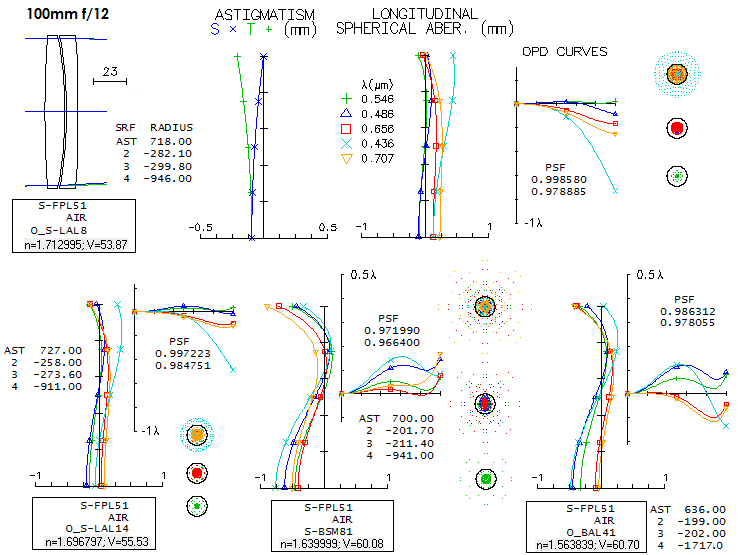
13-The TS-Optics Photoline 125mm f/7.8 apo puzzleThis refractor is advertised as having a doublet objective employing Ohara FPL53 paired with unspecified lanthanum glass. Those that play with designing this kind of lens objectives learn quickly that lanthanum glasses are generally suboptimal match to extra-disperion (ED) glasses. One reason - readilly apparent from a glance at the relative partial dispersion diagram (RPD) - is that they are higher on the diagram, i.e. will produce a correspondingly high amount of secondary spectrum (fluorite, FPL51 and, to a lesser extent, FK61 being exceptions in that they wouldn't produce secondary spectrum with a group of lanthanum glasses with lower RPD values). The other is that due to their relatively high index-to-Abbe# ratio, they require stronger inner lens radii, i.e. produce more of the residual higher order spherical aberration. Yet another minus is their violet dispersion, which typically causes the violet end run farther off from the rest of the colors. Yet, user acconts describe the telescope as "sharp" and "colorless", and it is marketed as comparable to a triplet color correction wise. What could explain this discrepancy? Choice of the lanthanum glass is determined by two factors: (1) its RPD differential, favoring those closest to the FPL53 level, for minimized secondary spectrum, and (2) relatively low violet end defocus. For a doublet, it is also necessary for it to have sufficient Abbe# differential, to minimize higher order spherical residual and spherochromatism. It also needs to satisfy physical and chemical requirements for fabrication and use. With respect to the first requirement, the best glass hand down is Ohara S-BSM81, producing zero secondary spectrum with FPL53 (there are also similar glasses from Schott and CDGM, but since their other properties are also similar, consideration will limit to Ohara glasses). However, it has insuficiently large Abbe# differential: at f/7.8 its design limit in the optimized wavelength is 0.22 wave P-V, due to the significant higher-order spherical residual. The best glass that can be found in the ATMOS base, with respect to the optical requirements, is S-LAL14. Image below shows what level of performance this lanthanum glass would produce when paired with FPL53 in both, doublet and triplet objective.
In a doublet (#1), correction at the given wavelengths level would be at the minimum required for the "true apo" if it wasn't for the large error in the violet g-line. Note that this "large error" compares to this line correction in a 100mm ~f/50 achromat, so it would be detectable only on bright targets. In a triplet (#2), there is no corrective action of the higher-order spherical residual on this wavelength anymore, hence the LA graph shows it more detached from the rest of the wavelengths (even if the triplet would be at f/7.8, the error would be still larger than in a doublet). This is perhaps why we don't see much of lanthanum in triplet objectives. For a more complete picture, shown are triplets employing BSM81 (#3) and BSL7 (Ohara BK7 equivalent, #4). With the former, even at f/6.5 there is no noticeable higher-order spherical residual, and no secondary spectrum. The latter, due to its stronger front inner radii (i.e. its lower Abbe# differential) does generate more higher order spherical and spherochromatism, but closer to f/7.8, at f/7.5 - which is the actual Takahashi TSA 120 design, save for the residual coma left in to compensate for coma in the dedicated reducer - it is better corrected than the lanthanum doublet, and the FPL53/BSM81 triplet even more so. In all, unless the TS Photoline uses some off-chart, custom lanthanum glass - which would be expensive - it is likely that it employs similar selective absorption coating as the one described under #10. The end result is a well performing telescope, and it is what matters.
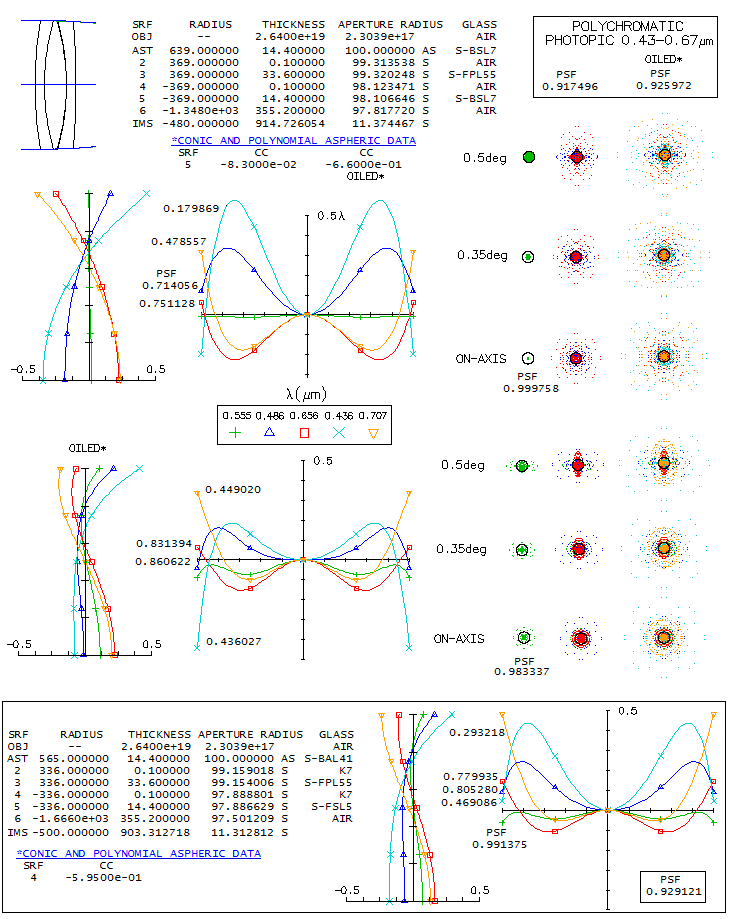
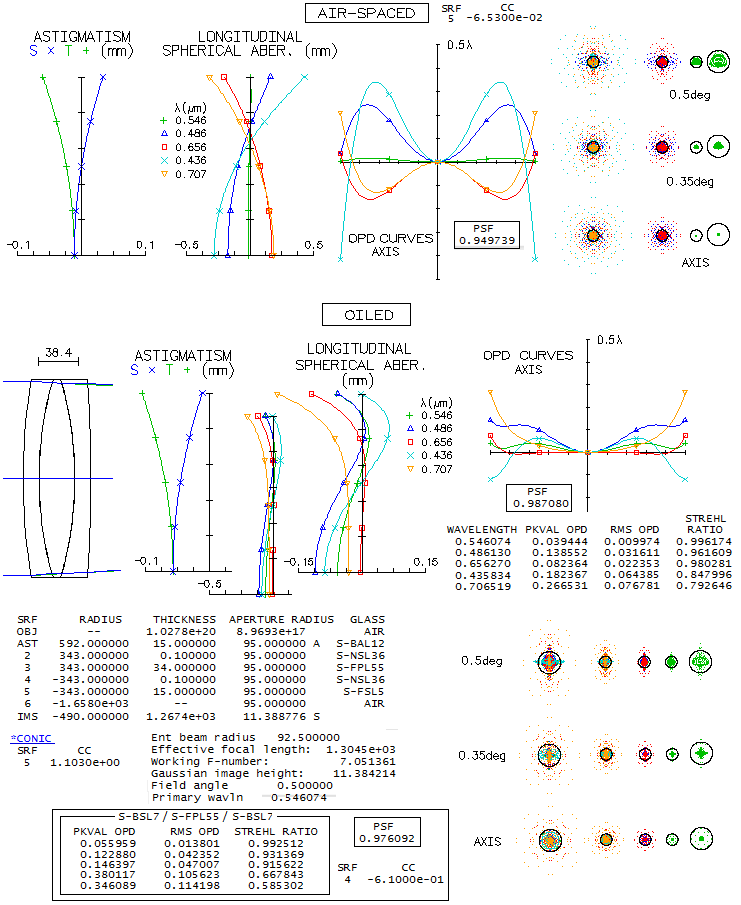
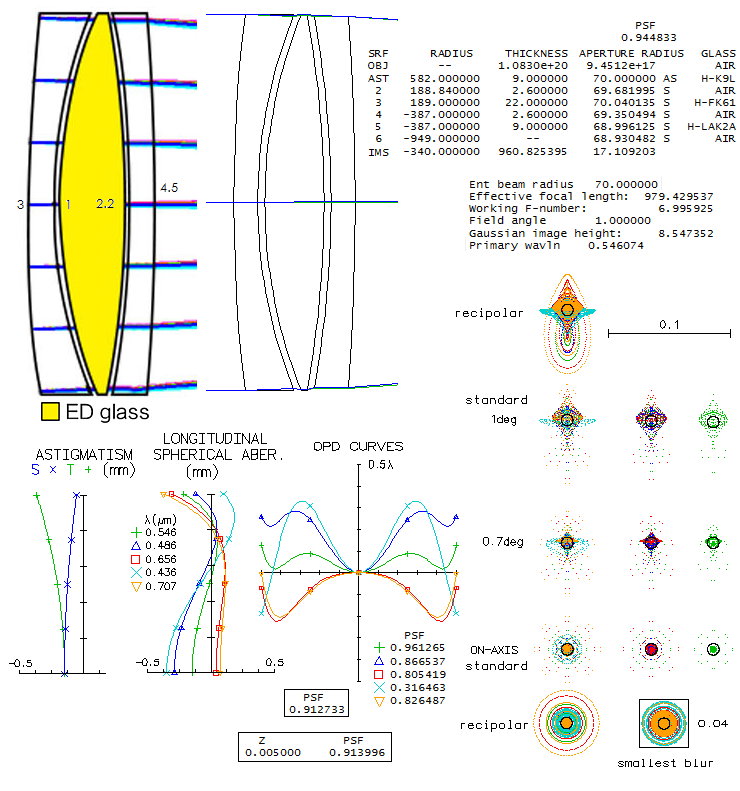
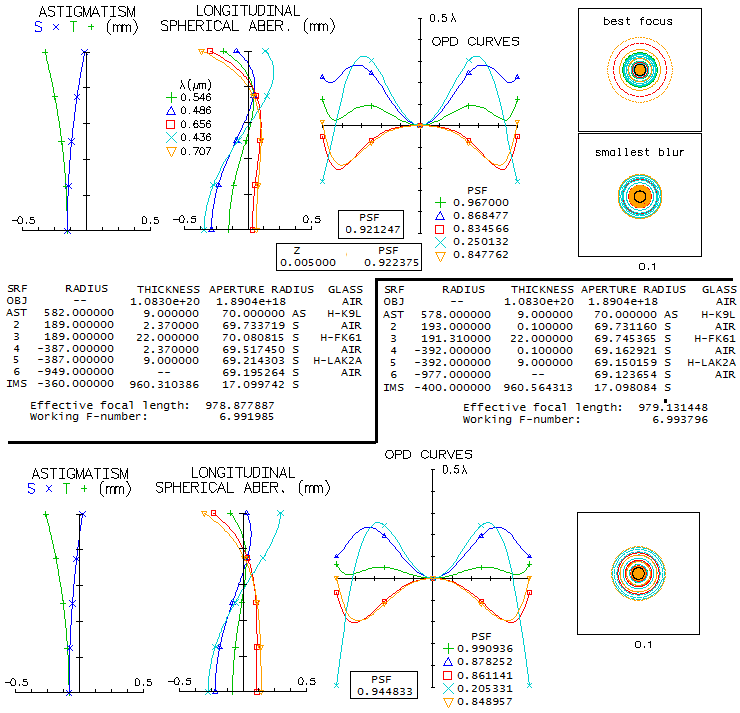
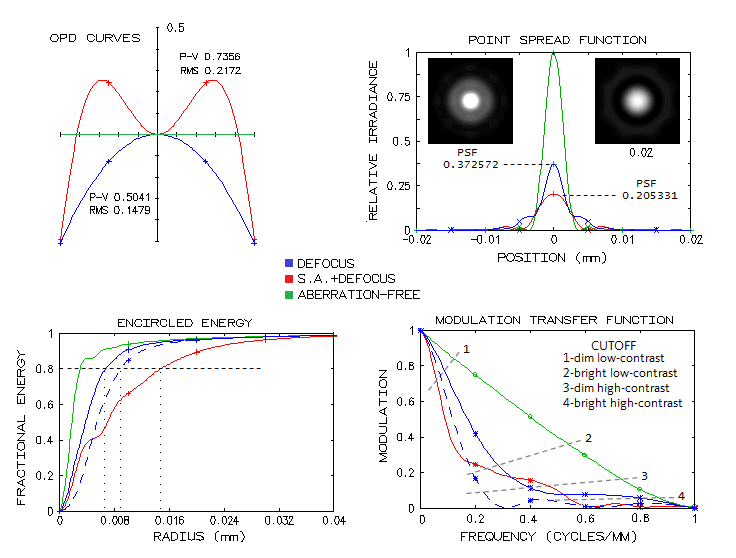
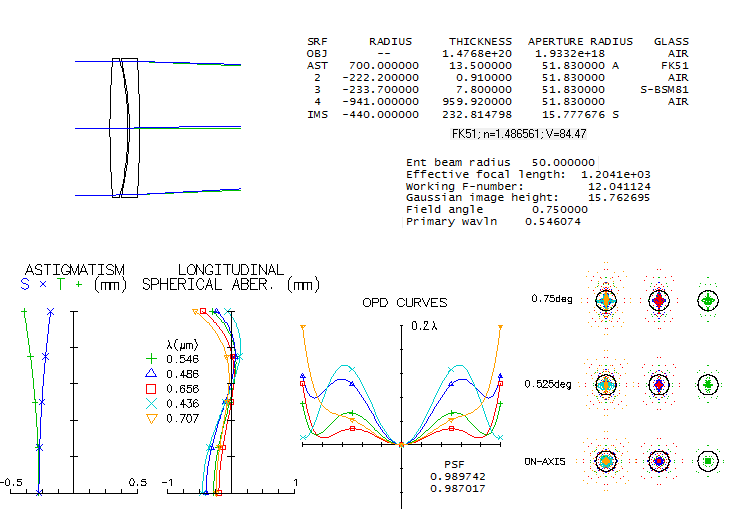
14-CFF 200mm f/6.5 APO TRIPLETWhat is known about this triplet is that uses Ohara FPL55 ED glass, and that has at least one aspherized surface. This means it can't be presented as the actual combination, but the choice of mating glasses is limited, due to FPL55 having lower relative partial dispersion (RPD) than other ED glasses, hence very few potential matching glasses for no appreciable secondary spectrum. The most likely choice is the cheapest, and also of the highest optical quality, S-BSL7, Ohara's equivalent of the Schott BK7. Image below shows BSL7/FPL55/BSL7 triplet with both, air and oil filled gaps (Schott K7 acts as oil substitute, having similar refractive index). Evidently, unlike the air-spaced lens, which has no noticeable higher-order spherical residual, in the oiled lens it is readily noticeable (the only difference in prescription, other than the gap medium, is the significantly stronger aspherization required with oiled triplet, mainly due to more 4th and 6th order spherical aberration at the 4th radius, as well as change of R1 to 644mm, to optimize color correction). Hoewer, it is a slight negative only in the optimized wavelength, while improving a bit the overall color correction - as the polychromatic Strehl (air-spaced graphs/spots are on top, oiled below).
Correction mode is, as usual, to have F and C lines nearly balanced, which is generally the best visual correction. A slight increase in the negative lens power pulls blue/violet and red away from the green (paraxial foci), in this case decreasing the error in violet and red, while increasing it in the blue, and would be better overall for CCD. The oiled lens qualifies as a "true apo" if judged by the errors in the five wavelengths - 0.8 Strehl or better in F and C, 0.4 or better in g and r (violet and deep red, respectively) - but still falls short of the "sensibly perfect" 0.95 polychromatic Strehl. Better part of it is caused by "only" 0.983 Strehl in the optimized wavelength; however, considering that it corresponds to a little more than 1/15 wave P-V of primary spherical aberration, no actual unit would be able to reach this Strehl value anyway). Doesn't seem to be possible to significantly reduce the higher-order residual in the optimized wavelength. Possibility to combine two different mating glasses with similar but opposite in sign RPD deviation from FPL55 is also very limited, due to its low position on the RPD diagram. One viable combination is with S-BAL41 in front, and S-FSL5 in rear (bottom; the reverse combination is not as good). While the overall collor correction is slightly lower, it is higher in the optimized wavelength. Aspheric required is similar, also on R4, which should be the aspherized surface in the actual lens, since it generates most of the 6th order spherical residual, significantly lowered by aspherizing.
15-SkyWatcher 190mm f/5.3 MAKSUTOV-NEWTONAll that is needed to come up with Maksutov-Newton design of an actuall telescope is its aperture and focal ratio. Practical variations in the corrector thickness around the standard 1/10 of the aperture diameter cause negligible effects on the final output, and for any given corrector thickness there is a single pair of radii that optimally corrects for spherical and chromatic aberration. Central obstruction size is not specified, but from the photos it is about 52mm in diameter. Image below shows the system outline, prescription, and optical output. Outer field vignetting (top left) is illustrated with the converging cone (green) against diagonal's surface (projected axially as a circle). Half a degree off vignetting is acceptable both visually and CCD, and one degree off only visually.
Design limit, with perfect surfaces, is shown on top. Polychromatic photopic Strehl exceeds 0.999, which implies that all nine wavelengths used for calculation (0.43-0.67 micron, 0.03 increment) are better than 0.999. The Strehl value reflects quality of the wavefront, independent of the central obstruction effect. In this case, central obstruction diameter is 27-28% of the aperture diameter, hence it reduces the central diffraction maxima relative intensity by a factor (1-0.2752), while the encircled energy drops by approximately (1-0.2752)2, due to the maxima's diameter reduction. This implies the PSF peak value of 0.923, and the encircled energy of ~0.854 for unit in a perfect aperture. The latter could be looked at as an indicator comparable to the Strehl for unobstructed aberrated wavefront, producing similar PSF encircled-energy wise, but keeping in mind that the obstructed PSF has smaller and brighter central maxima than that for the typical aberrations, and lower defocus sensitivity. The ray spot plots (left) show off-axis coma, a little over 1/2 wave P-V at 0.5° (8.8mm) off axis. That is nearly as good as f/9 paraboloid. Best field has 2200mm radius, convex toward mirror, resulting in a near negligible spot enlargement over flat field. Diffraction simulations (obstructed on top, unobstructed below) also show very little effect on image size for this field radius (0.5°). No telescope comes with perfect surfaces, and of particular interest here is how a radius error on the corrector affects both, spherical aberration and chromatic correction. Effects of changing the front radius to -354mm, which is less than 0.1% radius error, are shown on the bottom. The central line error now goes to 0.0273 wave RMS, equivalent of 0.091 wave of primary spherical. That lowers the central line Strehl to 0.968 (from 0.999440), and polychromatic Strehl to 0.962. In other words, the Strehl degradation factor due to the chromatism is still only 0.994. Conclusion is that the increase in spherical aberration induced by a radius error on the corrector surface is always far greater than the accompanying increase in the chromatic error.
16-ORION Eon 110mm f/6 ED doubletI said for the Omegon 110mm f/6 that it is probably the fastest ED doublet of that size, but it's not: there is just as fast Orion's 110mm f/6 Eon doublet using Ohara FPL51 and NBM51. While the mating short flint is identical in both, the Omegon uses a higher-grade ED glass: FPL53. Since it is also significantly slower, it must be having significantly better overall correction, right? Wrong. For one, FPL51 is higher on the relative partial dispersion diagram (RPD) than FPL53, hence having smaller differential vs. NBM51. That translates into a smaller secondary spectrum. More importantly, it matches the mating glass better in a way that its higher refractive index allows significantly more relaxed inner radii, resulting in markedly less of higher-order spherical aberration residual.
As a result, the e-line Strehl - design limit - is 0.997, vs. 0.961 with the
Omegon. Photopic polychromatic Strehl is 0.832 vs. 0.81, in the same order
(since the ratio for their central line Strehl is 1.037, assuming nearly
identical central line correction, chromatic
correction is slightly better in the latter; however, since both design limit
and tolerance favor the Eon, it is reasonably to assume it will have
a better central line correction average). Overall,
chromatic correction vise, the Eon is not quite at the level of a 100mm
f/15 achromat. 17-ES ED102 Essential Series TripletThis Explore Scientific 102mm f/7 triplet OTA comes at a price lower than many a doublet. Sure, its finish leaves something to be desired, but what really matters is how good it is - or can be - optically, considering that it uses a "common" ED glass, Hoya's FCD1? The mating glass isn't specified, but looking at a RPD diagram, there is a very few Hoya candidates that would practically cancell secondary spectrum. The best one seems to be BACD11, ordinary crown equivalent of the Schott N-SK11, listed by OSLO at 1.4 times the BK7 price. Here's what level of correction these two glasses produce.
Turns out, it easily passes the "true apo" requirements with both, error magnitude for the five wavelengths, and polychromatic Strehl: 0.975. Sure, that is at the design limit and 0.999 e-line Strehl. With the more realistic and still excellent 0.95 (1/8 wave P-V of primary spherical level), the poly-Strehl would drop down to "only" 0.926. But this means that no apochromatic lens has a chance to pass the 0.95 poly-Strehl requirement unless it is better than 0.95 in the optimized wavelength. And, chances are, most of them aren't. Contrast-wise, it shouldn't matter if the central line is, for instance, 0.99, and the rest of wavelengths 0.96, or the other way around, as long as they give the same 0.95 poly-Strehl. But it would be useful to specify both components, for it would give better indication of what is correction level of non-optimized wavelengths (that may not matter a lot with systems where spherochromatism dominates, producing what Roland Christen calls white, or whithish, chromatism, as opposed to defocused colored fringes with secondary spectrum, but still would be good to know). Back to the Explore Scientific "essential" triplet, if it uses this glass combination - and there is no good reason not to - optically it can be as good as any high-level apo (Hoya's BACD11 is listed as unavailable, but other near-identical glasses, like Chinese H-BaK6 are both, available and inexpensive). The unknown is its fabrication quality, which is what can make it or brake it in an actual unit. As an interesting aside, raytrace below shows how the choice of radius for minimizing spherical aberration can have significant effect on the overall correction (spherical aberration residual with all four inner radii equal is too high to allow for minimizing it by bending the mid lens into biconvex shape, so it has to be done with a change of one of the radii).
The rear two inner radii have much higher load of both, 4th and 6th order
spherical aberration, so even if they require lower nominal change for changing
4th order to be of a similar magnitude and of opposite sign to the 6th order,
the 6th-order spherical aberration imbalance created by that change limits the
best correction in the central line to 0.979 (bottom). That in turn causes the
polichromatic Strehl limit to be also significantly lower, 0.95 vs 0.97 with the
change in one of the front two inner radii (top). Note that the best diffraction
focus in either case doesn't coincide with the best central (e-line)
focus. 18-Celestron C90 Maksutov-CassegrainThe all-spherical 90mm Maksutov-Cassegrain had always been popular among amateurs. It's highly portable, inexpensive, has sufficient aperture to show more than department store telescopes, and - hey - it's a Mak! Celestron's 90mm Mak is, as nearly all others, Gregory-Maksutov type, i.e. with a silvered spot on the rear meniscus surface serving as secondary. In the past few decades it went through different shapes and looks, and nowadays it sells as an f/13.9 spotter. Its prescription hasn't been published (to my knowledge), but due to limitations imposed of this type of a system, it is pretty straightforward to come close to its actual specs, through a few iterations. Based on the approximate 100mm of back focus, the primary is about f/2.3, and the system raytrace is shown below (central obstruction is 0.3D).
With 0.94 polychromatic Strehl - same as its optimized line Strehl -
it does go as practically "color-free", but the design limit in the
optimized wavelength would leave something to be desired
for a highly corrected system.
It is a consequence of the fast primary, requiring strongly curved
meniscus producing significant higher-order spherical residual. The
actual units are probably closer to the "diffraction-limited" (0.80
Strehl), more so if the backfocus is a bit longer, as it could be, i.e.
the primary little faster.
This is probably why it goes as a "spotter" and not a telescope. For
better correction, the primary - and the final focal ratio - would have to be slower.
At 0.5° off axis, central diffraction
maxima is still well defined, with some low level coma and astigmatism
present. Even if the best image field seems to be strongly curved - 111mm radius -
the flat field image is not much more distorted this far off: credits
to the scope's slow focal ratio, making it relatively insensitive to
defocus. In all, if well made, this little instrument
certainly can do more than
little. 19-SkyWatcher EvoStar 120mm f/7.5 ED doublet apo confusionThis attractively priced refractor is quoted on the SkyWatcher US site - and probably from that source by some vendors as well - as being using Ohara FPL53 and Schott BK7 glasses (some vendors also hint at it having more than one ED element, and at least one quotes "ED BK7", but that's belonging to the marketing creativity domain). The problem is, these two glasses wouldn't produce acceptable performance level at this aperture size and focal ratio. They don't have large enough Abbe number differential, hence require very strongly curved inner radii for this focal ratio, resulting in unacceptably large higher-order spherical aberration residual. As shown below (top), their design limit in the optimized wavelength is slightly below 0.80 Strehl, and the polychromatic Strehl is yet lower (this is in the doublet with a positive element in front; with the reversed order, the required radii are even stronger). The RMS wavefront error implies 0.83 Strehl (with most wavefront deformation forms), but probably due to the high slope wavefront areas along the edge "wrinkle", showing on the 3-D wavefront map, the value is somewhat lower even at this moderate aberration level.
Assuming that the positive element is FPL53, and that its mating element is a Schott crown, the best - and practically only one - mating glass is N-ZK7 (it is also possible to mistype ZK7 to BK7). With it, the limit in optimized wavelength goes up to 0.977, and the overall chromatic correction is significantly better (bottom). In fact, it passes the "true apo" requirement setting the maximum allowed error in five widely separated wavelengths (less than λ/4 in F and C, less than λ/2 in the violet g and deep red r, with well corrected central wavelength; since originally it refers to primary spherical aberration, and today's objectives commonly have a mixture of primary and secondary spherical, with a significantly lower RMS to P-V wavefront error ratio, it is better to use the appropriate Strehl values: better than 0.80 for F/C and better than 0.40 for g/r - this objective has Strehl of 0.86, 0.84, 0.42 and 0.81 for F, C, g and r lines, respectively). Its polychromatic Strehl (photopic), however, is only 0.932. OSLO qoutes ZK7 price at 1.90 times the BK7 price, making it viable in that respect. ZK7 has somewhat less favorable violet dispersion than BK7, but due to the presence of relatively significant secondary spherical aberration, which is minimized by a similar amount of primary spherical, in effect bending the LA plots to the left toward high zones, the error is reduced.
If this objective is rescaled to a 150mm f/8 system - its bigger EVO brother -
it still holds quite well; in fact, a bit better than the 125mm f/7.5 system.
It passes the "true apo" criteria in all but the
violet g-line, which is at 0.165 wave RMS only marginaly higher than the
"true apo" limit for this wavelength (0.15 wave). The polychromatic
Strehl, at 0.94 (photopic), is just short of the "true apo" 0.95
minimum, in part due to its central line Strehl limit of 0.98. 20-TS-Optics 6" f/5.9 RFTAmong many telescopes on the Telescope-Express site is this rich-field refractor. It is advertised as having better correction than an ordinary achromat, to the extent that it claims chromatic aberration "barely visible" even on bright objects. Yet the glasses specified - K9 and F4 - are a plain crown-flint combination no different than those of ordinary achromats (CDGM H-K9 and H-F4 are near-equivalents of the Schott BK7/F2). The LA (longitudinal aberration) graph shown may be giving a hint to what is behind this puzzling claim (below, top left; the 0.633 micron wavelength is omitted latter as unneeded for the analysis).
The original LA graph (leftmost, boxed) shows that the optimized line is d-line (0.588 micron wavelength), although it is shown centered at its paraxial focus, which in the presence of spherical aberration never coincides with the best focus (in this case it would be approx. 0.5 and 0.8 zone focus, as shown on the right one of the two middle LA graphs). Using these same glasses produces practically identical LA graph (the original only has a wider scale), either centered on the d-line paraxial focus (left) or its best focus (right). As a consequence of optimizing d-line, e-line (0.546 micron) is sub-optimized, with over 1/3 wave P-V wavefront error at the best d-line focus, and 1/5 wave at the best e-line focus. However, taking for the optimized wavelength d-line, which is closer to F- and C-line than e-line, nominally decreases the F/C error with respect to the optimized wavelength. The OPD (optical path difference) graphs show that the P-V wavefront error of the averaged F and C lines (dashed line, top plot) is smaller than in the lens objective optimized for e-line (bottom plot; F and C lines are balanced here, as it in general should be, with the corresponding LA plot shown rightmost, in a box). The "gain" is, however, only superficial, since the error vs. yellow-green e-line, to which the day-light adapted eye is most sensitive (0.98 sensitivity, vs. 0.78 for d-line), is unchanged. The overall correction is actually worse, because of the sub-optimal e-line. The question which focus will eye prefer - the one with the lowest P-V error, or the one with the highest sensitivity - is easy to answer considering that the green light with 0.78 sensitivity sports 2/3 wave P-V wavefront error vs. e-line focus, and nearly 1/2 wave vs. d-line focus. There won't be preferred, or best focus, more so considering that in the more appropriate to night-time observing, mesopic mode, peak sensitivity shifts toward shorter green wavelengths. This e-to-d optimized line shift has a very little (positive) effect on the violet end, and the only way to hide this widely defocused light is to apply a special coating - such as lanthanum doped coatings - selectively absorbing that portion of the spectrum. The fact that the objective vas designed to have correction biased to the red may be due to the blue also being partly absorbed, in addition to mainly absorbed violet. This would improve contrast with this type of lens objective, but at a price of compromised color fidelity. It could still be inferior to an ordinary achromat in overall correction, but it can't be decided without knowing specific absorption bands and rates.
The combined ray spot plot (bottom right) is for the best d-line
focus, as well as the Strehl ratios shown (at the best e-line focus,
the e-line Strehl is 0.87). The F line (blue) has better Strehl despite
almost three times larger blur than the red C line, because the
former is mainly defocused spherical aberration (somewhat beyond
paraxial focus ad the location of best d-line focus), and and the latter
is predominantly defocus, with defocus having the same P-V magnitude as
primary spherical with eight times larger longitudinal aberration (nothing
that Strehl ratio at this aberration magnitude level is not a reliable
indicator of wavefront quality). This optimum line correction
hoopla turns costly when it comes to (photopic) polychromatic Strehl:
it is only 0.532 at its best diffraction focus, no better than a
100mm f/4 achromat. A 150mm f/5.9 achromat would have it 0.57. 21-Long Perng 90mm f/5.5 ED doublet refractorHeart of this very compact and attratively priced refractor is, according to Long Perng, doublet consisting of Ohara FPL51 ED glass and NBM51 short flint (the closest Schott short flint is KZFSN4). Below is what this glass combination produces when raytraced.
Due to the short flint being higher on the RPD (relative partial dispersion) diagram, some secondary spectrum is present: the common best F (0.486μ) and C (0.656μ) focus is less than 0.1mm from the best e-line focus. Common to short flints in general (and similar to lanthanum glasses) the violet is running away. The P-V wavefront error in F and C is about 3/4 wave of defocus, which puts it at the level of a 100mm f/16 achromat (f/14.4 for 90mm aperture). The violet g-line (0.436 micron) is at the level of a 100mm f/14.5 achromat, and deep red r-line (0.707 microns) a 100mm f/19 achromat. In all, it is similar to a 100mm f/16 achromat with respect to the nominal color error - bearing in mind that the aberration forms are different: defocused spherical vs. defocus - contrary to the statement at a vendor's site that it has chromatic correction comparable to f/7 achromat (no aperture specified, but according to raytrace the corresponding aperture would've been 44mm). Due to the large Abbe# differential, limit to the correction in the optimized e-line is very high: over 0.99 Strehl. Best image surface is of 200mm radius, concave toward objective (this means that the outer field would be in a flat-field eyepiece farther from its front focal plane, resulting in converging existing pencils, harder to accommodate to). On flat field, defocused ray spot plot at 1° off axis is about 3x5 Airy discs in e-line (0.022x0.038mm; it has vertically elongated shape due to the presence of astigmatism). This is defult secondary spectrum correction, with the errors in F and C nearly equal (considering that eye sensitivity is significantly higher to the blue line even in the daylight mode - 0.18 vs. 0.075 - practically optimal correction would have blue bias, but equaling F and C dates back from the time when the specific sensitivities haven't been measured). Error in the blue/violet can be reduced at the expense of increased error in the red. For instance, slightly weakening the inner radii (-187.3/-188.05) produces correction with 0.38 and 2.9 wave P-V in F and g-line, respectively, and 1.09 and 1.59 waves in the C and r-line (another way to control violet is to apply lanthanum doped coating for selective absorption). This may actually have been attempted, at least to some extent and at some time in the past (not necessarily properly), because some users reported excessive red end error in their units.
There is anoher version of this refractor marked with SD, instead of
ED. The site that states the ED unit's correction is at the level of a
f/7 achromat also states that the SD version uses the same ED glass.
Since in the commonly used terminology ED and SD (extra-dispersion vs.
super-dispersion) imply glasses with different dispersion properties -
and price of the SD unit is 80% higher, with the only mechanical
difference being in focuser type - they probably erred again. Assuming
that the SD glass is Ohara FPL53, a combination with the same mating glass
would produce near negligible improvement in the chromatic correction:
8% lower averaged F/C error, and 20% lower g-line error (but the optimized
line design limit goes down to 0.976 Strehl). Better chromatic correction is
possible with some other mating glasses. For instance, using Ohara's
LAL59 short flint (near equal to Schott KZFN2) produces 0.39 wave
P-V averaged F/C error, and 1.7 waves in the violet g-line. It is
comparable to a 100mm f/30 achromat in the F/C, and f/33 in the g-line
correction. Graph on FIG. 73
indicates as corresponding polychromatic Strehl 0.93-0.94, quite close
to the "sensibly perfect" >0.95. It is significantly better than ~0.86 poly
Strehl for the ED version. However, OSLO is a bit less optimistic. It gives
0.85 poly Strehl for the ED version (at 0.16mm from the best e-line focus toward
F/C focus), and 0.90 for the SD (0.1mm off best e-line focus). Part of the difference comes from
the long-focus achromats having practically design limit of 1 for the
optimized wavelength; that would bring the two respective poly Strehl
values to 0.855 and 0.922, respectively. Most of the rest of difference comes
from defocus having about 3% lower RMS wavefront error than spherical
aberration for given P-V error. This shows that fast systems like these two,
with spherical aberration as the dominant error, are not fully comparable
to long focus achromats based on the P-V wavefront error values. But
the numbers obtained that way remain reasonably close. 22-Synta 180mm f/15 Maksutov-CassegrainThis telescope comes in a few different brands - Celestron, SkyWatcher, Orion - but optically there is little or no difference between them. Synta hasn't published prescription for this system, but narrow constraints for this (Gregory) variety allow to come quite close to what the real system is - so close that there is no appreciable difference in the raytracing output. O.T.A. dimensions indicate ~f/2.7 primary which, with the back focus of about 0.6 times the mirror separation and known system focal ratio is all that's needed to reconstruct the system. The primary has to be aspherized, because it is impossible to have f/15 system at the given back focus: with spherical primary it is over f/17, and reducing it to f/15 by pulling the secondary a few mm farther away would shorten the back focus by nearly 100mm. Also, design limit in the optimized wavelength would have been little better than 0.05 wave RMS, which means that fabrication would require meeting very tight tolerances even for achievung λ/4 (0.0745 wave RMS) level. In order to have f/15 system with the given back focal length, the primary needs to be aspherised to about -0.25 conic (prolate ellipsoid). This also improves correction limit in the optimized wavelength, and cuts still very low coma in half (turning it from negative to positive, i.e. with the tail toward field edge).
Central obstruction by the secondary spot is 22% linear, but
the actual one is determined by the baffle tube around secondary,
and should be about 27%. Design limit in the optimized wavelength
is less than 1/10 wave or, more accurately, 1/44 wave RMS,
corresponding to less than 1/13 wave P-V of primary spherical
aberration (the P-V
error is superficially enlarged in presence of central obstruction,
since it is measured from the reference sphere vertex, where there
is no actual wavefront; also, secondary spherical has higher P-V to
RMS error ratio than primary). Half an inch off axis point image is
still "diffraction limited" (0.80 Strehl), which puts it at the
level of f/10.3 paraboloid. Colors are so tightly wrapped up that
the difference in Strehl ratio between optimized wavelength and
0.43-0.67μ spectral range is practically non-existent: 0.973.
Taking f/2.6 primary results in the back focal length somewhat
longer than 0.6 times the mirror separation (0.62) at f/15, with
slightly more coma (also, with 0.965 Strehl in optimized wavelength,
and about as high polychromatic Strehl). With small changes in the primary
speed and/or conic and corrector thickness,
the system can be entirely coma-free at the given back focus length.
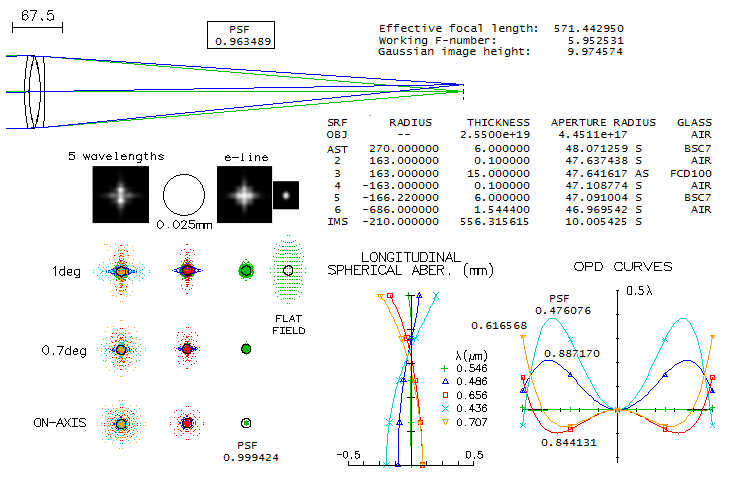
23-APM/LZOS 130mm f/6 "Superapo"APM/LZOS refractors use Russian glasses and fabrication. They are generaly based on the designs by Thomas Beck, but some may not be, and it is not known whether there were changes in the original designs. It is also unknown which glasses - except OK4 (for "osobiy kron", i.e. "special crown"), which is the only super-dispersion (SD) glass made by LZOS - are being used. What can be found online is that the matching glass is OK1 (UK vendor), or OF1 (for "special flint", customer review). The former is similar to the Shott N-PK51, with too small Abbe differential to produce viable output, and the later is the equivalent of the Schott KZFN2 short flint (obsolete), with more than half a wave P-V in F and C, and relatively poor overall chromatic correction. The two LZOS glasses that do fit as the possible matches are K8 (Schott BK7 near-equivalent) and BK8 (near-equivalent to the Schott N-PSK3). Their outputs with OK4 are shown below. Chromatic correction is modeled so that F and C line are nearly balanced in their error magnitude, with the violet and deep red determined by this requirement. It is considered generally optimal for visual use, although in low-light conditions typical for night time observing eye sensitivity in the blue-violet is significantly higher than in the red. This implies that the optimal mode here is toward photographic correction mode, in which correction of farther off wavelengths - particularly violet - is improved at a price of somewhat worsened F/C or even central line correction.
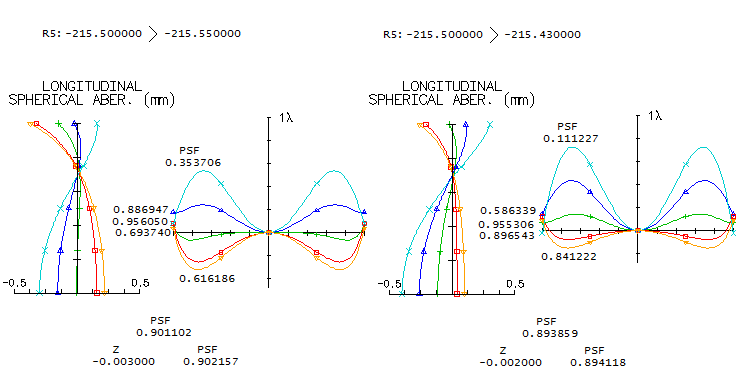
They are very similar, with the blue F and red C lines bordering the "true apo" requirement of no more than 1/4 wave P-V, i.e. 0.075 wave RMS error. So are their photopic polychromatic Strehl (9 wavelengths 430-670nm) values, only slightly higher for K8 (0.928 vs. 0.926 at the diffraction best focus, slightly defocused from the best e-line focus), with both remaining just below 0.93, hence falling short of the "sensibly perfect" (photopic sensitivity) 0.95. However, K8 has significantly lower error in violet: 0.61/0.182 vs. 0.96/0.264 P-V/RMS error, respectively. Note that the Strehl values for the violet g-line appear to be incorrect, not corresponding to the wavefront error values. It is a consequence of the Strehl - i.e. central diffraction intensity - becoming unreliable metric at large wavefront errors. Despite its lower Strehl, the K8 system encircles 80% of g-line energy in 0.0110mm radius circle, vs. 0.0124mm with BK8. Considering that K8 is also little cheaper, and of more consistent, high quality, it is very likely the mating glass in this case. Bear in mind that the above is design limit, i.e. output with all surfaces and spacings are perfect. Actual units are always more or less imperfect, with a lower overall correction level. To illustrate how sensitive are these lens objectives, raytrace below shows the effect of very minor imperfections in one of the inner radii (R5) of the K8/OK4/K8 lens, lowering the central line Strehl to little above 0.95.
Surface radius error of +0.023% induces undercorrection lowering the e-line Strehl to 0.956, and the poly Strehl to 0.902 (left). That's despite the violet g-line improving to just over 1/2 wave P-V (photopic eye sensitivity to it is only 0.012, or over 80 times lower than for the central line) and the corresponding Strehl seems to be close to its correct value this time. Surface error of -0.032% induces overcorrection lowering the central-line Strehl to 0.955, and the poly-Strehl to 0.894 (right). The blue F-line falls down to 0.59 Strehl, and the violet g-line error increases to 0.73 wave P-V (the corresponding Strehl value given by OSLO is again lower than it should be), while the error on the red end is significantly decreased. This shows why two different units of the same model can have noticeably different mode of chromatic error, i.e. that they can significantly differ in the magnitude of error for specific segments of the visual spectrum, even when their central line correction is practically identical.
This triplet is likely also used for the 130mm f/9 lens. At this f-ratio the polychromatic
Strehl is up to 0.97, and the overall correction easily meets the "true apo" criteria.
24-TS Photoline 96mm f/6 triplet apochromatTelescope Express describes this objective as "color clean", which is more accurate than the more common "color-free" (no refracting objective - and we could say no objective - is color-free). While no mating glass to its FCD100 core element is specified, the very likely choice is BSC7 (Hoya's equivalent of the Schott BK7 or Ohara BSL7 borosilicate crown). Simply, there is no cheaper and better quality glass available and, as shown below, it provides performance level fitting the description (note that the specifications are not those of the actual model, but the color correction of this glass combination cannot be significantly different).
At its design limit, the objective is comfortably within the "true apo" requirements, better than "diffraction limited" (0.80 Strehl) in F and C, and with less than 1/2 wave P-V (more accurate measure is 0.15 wave RMS) in g (436nm) and r (706nm) lines. Its photopic polychromatic Strehl is also above the "sensibly perfect" 0.95. Blur distortion due to field curvature is obvious at 1°, hence it would require flattener for wider CCD fields. Visually, astigmatic blur at 1° off is roughly twice the Airy disc diameter, or nearly 6 arc seconds times telescope magnification. To the average eye, it will start appearing non-stellar at about 3 arc minutes apparent size, or 30x magnification. That would be the very edge of the standard 50-degree 20mm eyepiece.
The inward
curving best image field would require accommodation which would
depend on eyepiece astigmatism, field curvature and focal length.
With 20mm Nagler
Plossl (patented design), which is a near flat-field design with
about 1 wave P-V of astigmatism at the field edge, required
accommodation is little over -1 diopter, which should be
easy enough for nearly everyone
(comparable to accommodating from infinity to little less than 1m;
negative accommodation results from the edge point being farther
from the field stop plane than the center point, thus having its
pencil slightly converging after passing through eyepiece, requiring
unnatural beyond-infinity relaxation of the eye lens).
With the 10mm Plossl, required accommodation would be four times as
much, but that portion of the field wouldn't be within the field
stop; the actual field edge of this eyepiece would require nearly identical
accommodtion as that of the 20mm unit. However, with wide-field
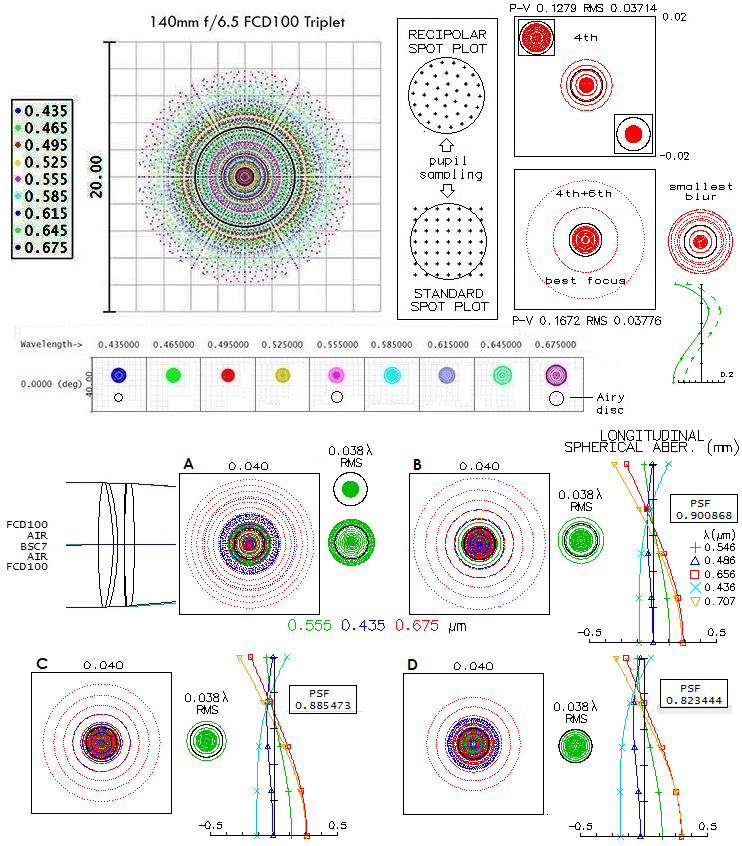
eyepieces accommodation would be generally more demanding. 25-140mm f/6.5 Super Triplet ApoThis configuration comes from SharpStar (which is also manufacturing it for the TS-Optics line), possibly Istar, and one or two other brends. Description of the objective by Istar is somewhat confusing and contradicting: for their two apos (140mm f/6.5 and 170mm f/7) the site states both fluoro-crown and fluoride, with lanthanum, both Hoya-made, but for their 170mm apo also CDGM (Chinese) lanthanum glass. There is also a "3xED" objective description (lanthanoids are abnormal glasses dispersion wide, but usually are not considered to belong to the ED class), which makes it uncertain whether it has a single, or two ED (or SD-super dispersion) elements. Sharpstar, on the other hand, directly states two ED elements, but makes no mention of the matching glass. So they may and may not have the same, NTN configuration (with two ED elements). With that uncertainty, both, double and single ED element objective will be considered. The ED glass is specified with Istar as Hoya FCD100 super-low dispersion glass, which indicates - considering the selling price - that it uses a single ED element. Still, since using PNP arrangement can't be rulled out, it will be considered first. No information on mating glass is given for the 140mm apo, and for the 170mm f/7 it is CDGM (Chinese) lanthanum. It is odd, since a FCD100 triplet doesn't need lanthanoid glass to produce a high-performance at f/6.5. Lanthanoids produce in general poor correction in violet, but since FCD100 can use the closest to it lanthanoids on the RPD diagram, that can be avoided. Still, lanthanoids are significantly more expensive, and not quite at the level of optical quality of the borosilicate crown (Schott N-BK7 and equivalents). A look at the RPD diagram shows that there is a relatively few glasses that would make a good match to FCD1000: Schott N-BK7 and equivalents, and a few lanthanum glasses that are close to its RPD value (Schott N-ZK7 is very similar in the output to BK7, a bit sharper in the optimized wavelength, but since BK7 is cheaper and more reliable quality-wise, it is the more likely choice). The lanthanum glasses seem to boil down to a few near-identical lanthanoids by different manufacturers: S-BSM811 (Ohara), N-LaK21 (Schott), LaCL60 (Hoya) and H-LaK4L (CDGM). Starting with BK7 - i.e. its Hoya equivalent BSC7 - as the matching element, the triplet could be executed with equal pairs of radii, i.e. suitable for oiled interspaces, or with a single inner radius changed in order to balance spherical aberration. The outputs are similar, but not identical (image below).
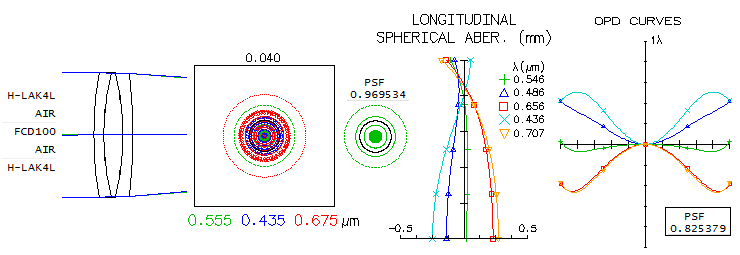
The objective suitable for oiling (top) passes the "true apo" minimum requirement with respect to the wavefront error in non-optimized wavelengths. However, mainly due to the relatively low central line Strehl, it falls short of the "sensibly perfect" 0.95 polychromatic Strehl (photopic, nine wavelengths from 430nm to 670nm). If its central line Strehl was, for instance, 0.99, the corresponding polychromatic Strehl would've been higher by a factor 0.99/0.97, i.e. 0.957 (note that the polychromatic Strehl is the highest at a point defocused by -0.005mm from the best central line focus). The objective below it, with three equal inner radii could be easier to fabricate. It has better color correction, but lower central line Strehl, resulting in a practically identical polychromatic Strehl. However, in night-time conditions, when vision shifts toward mesopic mode, with higher sensitivity to the blue and red, it would have an edge due to its better color correction. It may be a bit puzzling that an objective with the all color wavefronts comfortably within the "tru-apo" minimum requirements falls short of 0.95 Strehl, but it due to the fact that polychromatic Streh expresses overall correction level, not only chromatic correction. If the central line here would have 0.99 Strehl, polychromatic Strehl would increase to 0.965. Lanthanum glass is rarely used for triplets, because its greatest advantage - high Abbe# differential vs. ED glass, allowing for fast f-ratios - is dwarfed due to triplet's inherent lower requirements for high Abbe# differential. And other than that, lanthanums in general are not that great as matching glasses: their high-index to (relatively) low dispersion property partly offsets their high Abbe# differential advantage, and they typically have less than great correction in violet - the higher their Abbe# vs. ED glass, the more so. It is illustrated with two LA graphs (bottom), for different lanthanum elements as the mating glass in this triplet. Lanthanums closest to FCD100 on the RPD graph are also those with the lowest RPD differential, i.e. producing secondary-spectrum-free output. However, even if they do have higher Abbe# number differential vs. FCD100 than BSC7 (which is Hoya's equivalent of the Schott N-BK7), the gain in the central line correction is small. And despite somewhat higher central line Strehl, their polychromatic Strehl is not better than that for the BSC7-element objective (note that the triplet configuration changes going toward higher Abbe# differential lanthanums with the 2nd and 3rd element needed to correct for chromatism taking meniscus form). The LA graphs illustrate the main disadvantage of lanthanum glasses: as Abbe# differential increases from Hoya's M-BACD5N (low-melt temperature glass, suitable for molding, a better mactch than BACDN5) to CDGM H-Lak12, the blue and red slide away from the green, and color defocus - particularly in the violet - becomes larger. The blue-red separation is what ultimately produces secondary spectrum, which is already detectable with H-Lak12. Considering that lanthanums close to FCD100 on the RPD diagram do not offer advantage in overall correction over BS7, the latter is a more likely choice, being cheaper and of highest optical quality. Does the PNP arrangement, with two ED elements necessarily makes a triplet "super", i.e. better corrected than the single-ED element NPN? Putting the same glasses into a NPN triplet with only a single inner radius changed and identical f-number, gives as an answer "no".
Mainly due to significantly lower relative change in the radius needed, the higher order spherical residual is significantly lower, practically negligible, allowing for a significantly higher Strehl in the optimized wavelength. As a result, the polychromatic Strehl here is over 0.95, impying "sensibly perfect" correction at the design limit. Replacing BSC7 with a suitable lanthanoid - let it be the Chinese H-LaK4L - results in a significantly greater error in the violet, but tighter correction in the other colors, and a higher poly-Strehl (bottom). The PNP arrangement could have as low - or even lower - higher order spherical residual only if employing wider interspace, like Takahashi TOA. Considering the low-bracket price of this refractor, it is unlikely. iStar objective cell does have its vertical adjustment screws somewhat more widely separated for the first two elements, but it is not more than a few mm, probably to accommodate spacing at the first two inner radii, with R3 significantly more strongly curved than R2 (objective cross-section above -2nd from top - has the two surfaces touching at the edge, possibly slighty overlapping). It indicates that the more likely arrangement would be the one with unequal R2/R3. Spacing increase to as much as 11mm results in only marginal improvement in color correction. However, in this particular glass arrangement, with the most of higher order spherical residual coming from the third surface, even a relatively small gap between R2 and R3 can have it significantly reduced.
With BSC7 as the mid element (top), e-line correction is now as good as 0.995 with the polychromatic Strehl exceeding 0.96. The gap is small enough not to impose significantly more stringent requirements with respect to cell fabrication and lens alignment, which should qualify this type of arrangement as the one most likely used for this objective. And replacing BSC7 with H-LaK4L (bottom) results in not quite as good color correction, as well as significantly more of the higher-order spherical residual, setting the central wavelength design limit at below 0.96 Strehl. As a result, the poly Strehl drops to 0.924. In all, the double FCD100 in combination with BSC7 seems to be the closest to the actual design. This conclusion is also backed by its ray spot plots also being closer to those published by iStar than for the rest of objectives (in fact, the only ones close enough). Image below shows the published spots: the large one is a combined spot for the wavelengths specified, and the small spots are for the isolated wavelengths. The latter are quite small, not revealing enough of structure, but their diameter can be determined fairly accurately. The spots are not the standard ray spot plots, resulting from the usual square grid pattern for ray sampling of entrance pupil, but recipolar spots, resulting from a circular (recipolar in OSLO, hexapolar in Zemax) pupil sampling.
It should be noted that the black circle on the combined spot does not correspond to the central wavelength's Airy disc. Its diameter, according to the scale, is 7.4 microns, corresponding to 0.467 micron wavelength - probably an omission. At right, the 0.555 micron spot has some general resemblance to the recipolar spot for 1/8 wave P-V of 4th order spherical aberration at best focus (smallect blur focus - top corner, defocus - bottom), as well as to the smallest blur spot for the corresponding (0.037-0.038 wave RMS) level of balanced 4th/6th order spherical aberration. Defocus to the smallest blur focus for f/6.5 system (dashed LA plot) is 0.1mm. Assuming that the system has balanced 4th/6th spherical (it can't be 4th order alone with this, and most other designes at this f-ratio), design limit in this case is much lower than 0.038 wave RMS. That may indicate that the published central line spot is a result of refocusing to the smallest blur (and larger wavefront error) focus. If so, the published blur size indicates the central line error of 0.027 wave RMS, or so. Since the published blur is, due to its small size, unclear (recipolar blur for radially simmetrical aberrations consists only of concentric circles; when they are close enough they merge together, but they are generally no solid areas of different density), will somewhat larger central line error of 0.038 wave RMS, already illustrated above. For simplicity, will look only at the central, and two end wavelengths. If the needed spot size is accomplished by defocusing toward blue/violet (A below), the violet blur becomes smaller than the red, but it is still significantly larger than the green (as the blur above shows, the corresponding error is also nearly three times larger than the 0.038 wave RMS level). If, instead, 0.038 wave RMS of undercorrection is induced (B), the violet blur becomes comparable in size to the green, but the red blur is still about twice larger than the published one. Widening the blue/violet-to-red separation by slightly strenghtening one of the convex radii, while keeping the central line error nearly unchanged, further reduces the red blur, while keeping the violet close to the green size-wise (C, D). Reducing the central line error would reduce both red and violet blur, but it is already close enough considering that no actual gaps are known. It doesn't mean that this arrangement, or glasses, are those employed in the actual design, but they are close enough to allow for that possibility. However, lowering/evening the blurs' size - as it usually does - results in suboptimal color correction, since it is a common place with spherical aberration that the best focus (i.e. the one with the lowest wavefront error) does not coincide with the smallest blur focus. Pushing the crossing area higher on the LA graph will diminish the blur size, but increase the wavefront error. It would produce fairly similar spots with the NPN design above, using H-LaK4L as mating glass, but at a price of a big drop in the color correction level (below).
While it is very unlikely that diminishing the spot size at this cost would be used in any professional design, it illustrates how little the spot size alone can mean, and that - when it comes to apo objectives - the smaller is not necessarily the better, and when it comes to spherochromatism it is always the worse. Finally, looking at a double ED objective with Chinese glasses, with H-FK61 being nearly certain - considering price - for the ED glass choice, the likely matching glass, which should also be inexpensive, is H-ZK7, listed in OSLO catalog as 1.3 times the price of the Chinese BK7 equivalent. Raytrace below shows that a 140mm f/6.5 objective of this kind is a borderline "true-apo" (on its design limit, of course).
Its poly-Strehl (photopic) falls just short of 0.94, but the five
widely separated wavelengths used for the wavefront error criteria
satisfy: (1) the well corrected central line requirement , (2) less than 1/4 wave
P-V (more accurate if replaced by 0.80 Strehl) in F (486nm) and C (656nm)
lines, and (3) less than 1/2 wave P-V (more accurate if replaced by
0.40 Strehl) in g (436nm) and r (707nm) lines. Despite having 2/3
waves P-V in the g-line, its Strehl is 0.41, slightly better than
for 1/2 wave P-V of defocus. This is a consequence of different
wavefront shapes, creating different P-V to RMS wavefront ratios,
and different levels of energy spread. The smaller
average error over most of the inner area with partly defocused spherical
aberration causes less of energy loss than the larger average error
over that area with defocus error of identical
P-V value. In this case, as the MTF plots show, 2/3 wave P-V of
partly defocused spherical aberration (plots at right) in the g-line has roughly
comparable contrast transfer to that of 1/2 wave P-V of defocus.
In fact, since high frequencies with contrast transfer hovering
close to zero, are unlikely to be resolved in field conditions,
an instrument with this level of spherical aberration would
perform better, and outresolve the one with 1/2 wave P-V of defocus on bright
low-contrast details (BLC cutoff line).
26-Takahashi FC100DZ 100mm f/8 fluorite apo doubletSometimes described as the "best doublet ever", this refractor is marketed as consisting of a rear fluorite element and a high-index/low-dispersion front element. The latter generally describes lanthanoid glasses. Fluoride is "privileged" vs. other SD (super-low dispersion) glasses in being higher on the RPD (relative partial dispersion) diagram, hance being able to use low Abbe# glasses - for a large Abbe# differential - without introducing secondary spectrum. Lanthanoids in general tend to be more or less loose in the violet; those that perform the best in that respect with fluorite are having refractive index of ~1.697 and ~55.5 dispersion (e-line). They include Schott N-Lak14, Hoya Lac14, CDGM H-Lak12 and Ohara S-Lal14. While not the best - differences are small - it is the Ohara glass that produces longitudinal aberration graph nearly identical to the one published (below).
The LA graph differs from the published one only in having the
violet-blue lines bending in somewhat more strongly toward edge
(that reduces the aberration), which indicates somewhat smaller
Abbe# differential than the actual glass. But the overall performance level is nearly
identical. Note that the Takahashi graph may be a drawing of the
actual raytrace output; it is shown on a large horizontal scale to leave
a visual impression of the very tightly bound together color lines.
Correction can be varied by slightly changing lens' positive
or negative radii; for instance, violet g-line can have
Strehl up to 0.72, with the C-line Strehl down to 0.94+ and
the F-line Strehl practically unchanged. But those intricacies
are beyond fabrication schedule. The polychromatic Strehl (photopic,
430-670m) is 0.975 at its limit. Needles to say, this particular
match does qualify as a "true apo". 27-Agema 130mm f/8 fluorite apo refractorThe Strehl graph across visual spectrum displayed on Agema's web site shows this doublet to be superior to - among others - Zeiss APQ 130 f/7.7 and Takahashi 120mm f/7.5 TSA triplets. The level of correction is "impossible" for a doublet; there are glasses which in combination with fluorite would rate as a "true apo", but not even close to the Strehl above 0.95 from F to C, and beyond. Luckily, the answer to this puzzle comes in a form of patent application by Eduard Trygubov, Agema's owner (US2018/0149832 A1). It describes an ingenious doublet which uses a wide air gap to bring all colors tightly together, and then corrects unacceptably high secondary and tertiary spherical aberration by puting higher-order aspheric on the front surface. The actual design is, according to the published graph, not quite identical to the patent design, but the difference is very small.
The entire visual spectrum is comfortably within 1/5 wave P-V wavefront error, with the e-line Strehl rounding off to 0.9999 and the polychromatic Strehl (photopic, 430-670nm) reaching 0.987. The A4 term (AD in OSLO notation) is for lower-order spherical aberration which easily can be handled with small changes in one of the inner radii, but in this case it is of opposite sign to the other two terms, which means it decreases required depth of the aspheric (also, it is just another form of expressing conic, with the one needed to replace A4 being 0.31 - oblate ellipsoid). Since these are xn curves, with n positive integer, the maximum depth is at the edge, given here by a product An65n; without the A4 term, A6 and A8 combined (AE and AF, respectively) would come to 0.00283mm, and with it the maximum depth is 0.002mm (absolute values), or nearly 4 waves. This, however, is not the least amount of aspherization possible. Analogous to the Schmidt corrector, these xn terms bring together paraxial foci of different wavelengths, where the error for non-optimized wavelengths is four times larger than at the best focus, which is for primary spherical the 0.707 zone focus. In order to bring color foci together at that zone, radius term is introduced which effectively induces needed defocus by altering the profile shape. In this case, that would amount to setting the A4 value to be equal to the sum of A6 and A8, which would result in zero aspherization at the edge. As illustrated below, the amount of glass to be removed is significantly smaller, not only due to the smaller maximum depth, but also due to it being at the inner zone.
Aspherization A is the one used in patent application, and B is the one that minimizes glass removal. Note that the curves show grossly exaggerated profiles, but the relative depth difference is, at least roughly, similar to the actual. Aspherization A is not as smooth as it appears, as it shows its form when applied to a concave surface (smaller graph below). Bottom graphs show that there is no difference in correction level between the two (error in violet and deep red are somewhat larger with B to minimize the F/C error; they can't be all minimized at the same time). Similar reduction could be achieved with A6 and A8 alone. Since they are negative in sign, the curve they indicate is to the left of the actual (spherical) surface, i.e. glass should be grown on the sphere of that radius in order to form required asphere. That is easily done in raytracing, but the actual surface would require a slightly weaker sphere as the starting point. The best option is, again, zero aspherization at the edge. The sphere that fits that requirement has a radius of 538.77mm, and the required maximumm depth larger than in the previous case, but still requires significantly less of glass removal than the patent design (below). Note that the sphere required to match the aspheric turns concave due to enormously strong curves (f/0.25 base sphere), but the profile of aspheric vs. sphere deviation is similar to the actual deviation).
Performance remains practically unchanged, with the poly-Strehl rounding off to 0.99. Prescription shown uses the original radius - which means that the raytracing surface is suspended above the sphere - but there would be no difference if R1 was 538.77mm as required for actually fabricating the asphere. Of course, in order for the Strehl to be actually high as shown, all surfaces, centers and separations need to be extremely close to those of the design. If, for instance, the central wavelength measures "only" up to 0.96 Strehl (corresponding to less than 1/9 wave P-V of primary spherical aberration), one end of the spectrum would worsen, the other improve, but the poly-Strehl would be reduced by a 0.96 factor.
It is interesting that these two glasses would easily produce a
"true apo" if aspherized as a contact doublet. But design limit
in the violet g-line (436nm) would have been only around 0.45 Strehl,
and about 0.85 in the red r-line (707nm). Since F and C would
have it ~0.95 and ~0.93, respectively, the whole trouble of
using wide gap was endured only to bring the two spectral ends -
primarily the violet - above 0.9 Strehl as well. It brought its
polychromatic Strehl (photopic) - as design limit - to 0.99, practically at the level
of the special wide-gap(s) triplets like Takahashi TOA. A testament that
only extraordinary
drive can produce extraordinary achievement. 28 - 160mm TEC fluorite apo, f/11 doublet vs. f/7 tripletThe two fluorite apos offered by TEC are the top line instruments, one geared toward wider field, the other toward near-ultimate correction level (appropriately named by TEC "planetary"). How much better corrected could the long doublet be? While no specific answer to this question is possible without published prescriptions, playing with matching glasses that are in a very narrow circle of the best matches can give a good idea of it. Image below shows 160mm f/11 fluorite doublet with Ohara S-BSM14 mating glass (top), f/7 fluorite triplet using the same mating glass with all four inner radii equal (middle) and the triplet optimized by bending the mid element. Linear field is nearly identical for all three, which means that the triplet has correspondingly larger angular field. Note that the triplet is oil-spaced, so R2=R3 and R4=R5 (S-NSL36 is used as oil surogate, having similar optical properties as commonly used oils; raytracing-wise, there is little difference if the gaps are filled with air instead). The choice of mating glass was based on the quality of chromatic correction; with the doublet, slow focal ratio indicates that the mating glass is not lanthanoid, since it is not necessary, and would result in generally worse chromatic correction than the BSM14 (borosilicate medium-index crown, near-equivalent of the Schott N-SK14).
Raytrace shows that the doublet has indeed significantly better correction than the triplet with all four inner radii equal (middle; OPD graph has added individual Strehl values for the four wavelengths, except e-line, whose Strehl is shown at left, below system prescription, together with polychromatic Strehl). This is mainly caused by the latter having more of the higher-order spherical aberration residual, limiting its e-line Strehl to 0.965. Difference in chromatic correction between the two is for all practical purposes undetectable contrast-wise (assuming zero error in the central line, chromatic correction alone comes to 0.99 vs. 0.97 poly-Strehl degradation factor for the doublet and triplet, respectively), but in most critical applications the triplet is a slightly more "colorful" visually. Also, uncorrected lower-order spherical requires strong aspheric on the front surface (oblate ellisoid; front surface is preferred because aspherizing it also reduces the higher-order spherical aberration residual). Showed in the box to the right, some other combinations viable with respect to secondary spectrum correction would have better correction in the e-line, but their larger error in un-optimized wavelengths - primarily F and C - mainly cancels out that advantage when it comes to the overall correction level expressed with polychromatic Strehl ratio (nine evenly spaced wavelengths from 430nm to 670nm, photopic sensitivity). Best result is obtained by reducing spherical aberration load bending the mid element (bottom). Usually, either the first, or second inner pair of radii generates significantly more of spherical aberration than the other one. By relaxing that pair, while at the same time making the other stronger, in order to nearly preserve longitudinal chromatic correction, at some point both pairs contribute roughly similar amount of the aberration, but the total is minimized. In this case, the front pair had to be made stronger, and the rear pair weaker. This way, it may be possible to eliminate spherical aberration entirely; it wasn't possible here, but it allowed for a considerably less aspherised front surface, in addition to significantly lower higher-order spherical residual. The e-line Strehl is now 0.986, and the poly-Strehl is 0.954. This triplet meets both "true apo" criteria, the one requiring F and C lines be no more than 1/4 wave P-V, with g and r lines no more than 1/2 wave, as well as the poly-Strehl of 0.95, or higher. It is still behind the doublet with respect to the overall correction level limit, but both are now within the "sensibly perfect" domain. An important practical aspect are their respective fabrication/alignment tolerances.
As post scriptum, Yuri Petrunin let me know the mating glass
is not the one used here, but is "very close". It could be one
of the handful of nearly identical glasses; Hoya's BACD14 seems
to have little better correction in the violet, but that's how far
guessing can go. Also, Yuri said the actual lenses are significantly
thicker (17 and 22mm the doublet), due to fabrication requirements. It has no
appreciable effect on the final raytrace output. 29 - Zeiss Meniscas 150/2250This Zeiss Makutov-Cassegrain telescope had seen its first light more than half a century ago. when I first time saw it on a magazine photo, mounted and with a multiple eyepiece holder, it looked to me as a perfect telescope in every respect. There is no published prescription, but since it is a Maksutov-Cassegrain system, it can be reconstructed to a close approximation based on the optical tube configuration. The tube (left, shown with dew shield attached) indicates ~f/4 primary, with the secondary at about 3/4 of primary's focal length.
Out of three possible configurations, two can fit into this scheme: a Cassegrain-like system with the secondary having different surface curvature than rear meniscus surface, and a Gregorian-like system. The third one, standard configuration known as Gregory-Maksutov would require a fast f/2.6 primary, with the meniscus-to-primary separation little more than 2/3 of that indicated by the optical tube. That would leave us with the first two, and actually only one: the Gregorian arrengement also would require fast primary, ~f/2.45, requiring aspherization, but with significant coma and astigmatism limiting "difraction-limited" (0.80 Strehl) field to 0.06° radius. It cannot be remedied, even with use of higher-order aspherics. Also, design limit in the central wavelength is only 0.925 Strehl, even with -0.5 conic on the primary (higher conic would improve central line correction, but would require wider meniscus-to-primary separation, which is already becoming too wide for the tube configuration). That leaves a system with the secondary surface on the meniscus of different radius than of the meniscus rear surface. Raytrace below shows all three systems: the standard (top), the most likely configuration (middle) and the Gregorian (bottom). The standard configuration doesn't fit physically, but it is given for comparison.
All three systems have nearly 40% central obstruction, which
corresponds to the size of the aluminized spot on the actual units.
The minimum secondary size for the middle arrangement is 42mm, or
28% by diameter, but the spot is significantly larger than needed
most likely for baffling
purposes (it seems as if there was no secondary baffle employed).
Design correction limit for the mid arrangement is at the 0.99
Strehl level, extending over nearly entire
1-degree field. 30 - MTF comparisonThe wavefront error figures alone - as well as based on them Strehl values - do not allow for direct comparison of systems with and without central obstruction. For that, we need an indicator based on intensity distribution, such as MTF. Here, the eight largest systems from above, obstructed and unobstructed, were put in a direct comparison with respect to their contrast transfer. The MTF plots are polychromatic for all, with the cutoff point taken to be the frequency at which contrast transfer drops to 1%. That frequency is then corrected for the focal ratio and aperture in order to have different systems brought to the common relative MTF frequency. It was done because polychromatic MTF commonly has cutoff frequency significantly higher than MTF of the central wavelength, with the added frequency range having the contrast lingering just above zero. For all practical purposes, that contrast transfer is zero, and placing the cutoff at 1% both, excludes that quasi transfer range and, possibly, makes the cutoff point more accurate. To the eight systems from above is added Zeiss 200mm f/15 AS objective - an enchanced achromat - to show how such large long-focus lens objective compares to these modern systems. Note that the MTF plots are based on the design limit, hence do not reflect quality of fabrication, which is always important factor (it generally includes thermal menagement). Also, the seeing factor is not taken into account, which means that smaller apertures will do somewhat better in field conditions than what the purely optical output indicates (how much, depends on the seeing quality).
The two systems clearly ahead of the rest are two 10-inch Maksutov-Cassegrain
designs, from Aries and Astro-Physics. The former is significantly better
than the latter in part due to its larger central obstruction (high
frequency range), but mostly due to its very high central line
correction level. Plots for the rest of systems form a group in which
the difference is significant between the top and bottom systems, but
transition from one end to the other is gradual. In addition to
contrast transfer over the range of >1% contrast frequencies for each
system, as an image quality criterion shown is their approximate
resolving limit for bright low-contrast (i.e. planetary) details.
Here, the Zeiss comes at the bottom end (it has only about 20% less
secondary spectrum than standard achromat, despite it often being
quoted as having it reduced in half). Mewlon 210 is a bit better than
TEC 160mm f/11 fluorite doublet, the latter being limited only by
the aperture. Synta 180mm f/15 Maksutov-Cassegrain is a bit better
than both, and then come three systems somewhat more separated from
these, as well as among themselves: 180mm f/7 apo triplet, 190mm f/5.3 Maksutov-Newton,
and 200mm f/6.5 apo triplet. The 10-inch AP Maksutov-Cassegrain has
substantially higher resolution limit, and the Aries 10-inch version
is still significantly better (number in brackets where the systems
are listed is the order # of the system on the page).
31 - Big apo triplet: run-off-the mill vs. high-endWhat separates high-end apo from the run-of-the-mill kind is using so called "super-dispersion" (SD) vs. "extra-dispersion" (ED) glass. In addition to SD glass, performance of the former can be enchanced by aspherizing a surface, oiling interspaces, and/or significantly changing configuration. Aspherizing alone, similarly to a configuration change, does not necessarily enchance performance vs. all-spherical lens objective, but it is fair to assume that it does in the real world, simply because it adds to the cost. Oiling, on the other hand, always enchances performance by minimizing the effect of surface imperfections and internal reflections. There is usually at least some difference in the fit and finish favoring the high-end apo, but quality in that respect is generally high for both. To illustrate possible difference between "high-end" and "run-off-the-mill" a two reconstructed objectives are used: one based on the new Chinese 185mm f/7 air-spaced triplet (Askar), and the other based on the CFF 185mm f/6.8 oiled triplet, for the sake of comparison rescaled to f/7. Neither has a published prescription; the latter uses Ohara FPL55 SD glass, and the latter - considering its low price - CDGM HK61 ED glass for its core element. The latter also has published lens configuration, which makes reconstruction easier (the published ray spot plots are practically limited to those for 0.44 micron wavelength, with 1x field flattener added). Starting with the Askar, the published lens configuration indicates 3rd-to-4th radius ratio of ~1.55, two pairs of equal inner radii and the two gaps between the lenses of about 3mm. Only a single glass combination out of the glasses listed in the OSLO Edu catalog matches that geometry: H-BaK8 in front, (a Schott N-BaK1 equivalent), H-FK61 in the middle, and H-K9L (Schott N-BK7 equivalent) in the rear. No other combination comes close enough (reverse combination of the same glasses, with 2.78mm gaps, is practically as good, the only other difference being somewhat weaker front radius, at 739mm, and stronger rear radius, at -1790mm). Raytrace output for this combination (below) comes close to the "true apo" level with respect to wavefront errors in the four widely separated wavelengths, except in the violet g-line which is at a 1.5 wave P-V level. The corresponding photopic polychromatic Strehl is 0.92. The violet line has negligible effect on its value, due to the very low eye sensitivity to it; what is mostly causing Strehl degradation are relatively large errors in the blue and red. Adding a simple zero-power field-flattener (bottom) has no appreciable effect on correction, but does add some low-level coma. That could explain a statement given in the official description, that this flattener corrects for coma of the objective - which shouldn't have any if properly designed. In that it is similar to the Takahashi TSA 102mm f/8 triplet, which also has some residual coma left in the objective and corrected with the dedicated field flattener. The front radius of the published configuration could be a bit weaker (~5% or so, hard to pinpoint with the thick lines of the published drawing) than that in the raytrace model, possibly indicating some residual coma left in (coma is corrected by balancing strengths of the 1st and last radius, with no effect on the chromatic correction).
This particular flattener does not alter the size of ray spot plots, including that for g-line. Assuming it is the case with the actual unit, there is a discrepancy with respect to the published 0.44 micron ray spot plot size, which is about twice smaller. For the given wavefront error in g-line, the blur size vary with the focus location: bellow the LA graph are ray spot plots for (from left) paraxial, actual, (since the violet g-line is somewhat defocused), half the longitudinal aberration (best focus), 3/4 longitudinal aberration (smallest blur) and marginal ray focus. The one for 1/2 LA (about 0.65 zone focus) is about twice smaller; the corresponding correction mode would reduce error in the violet, but would significantly increase it in all other wavelenths. So that remains an open question; it is possible that the smallest blurs are presented, even if the system is designed around best focus. Also, it is certainly possible that the correction mode differs from the one chosen here, with the error in F and C nearly balanced. By a slight strengthening of the positive power the blue/violet are shifted closer, and the red farther away; it would reduce the error for the former, but would increase it for the latter. For example, as shown below, if R1 is made 2mm stronger, the resulting combined blur reduces to ~46 microns at the best focus location, but the overal chromatic correction would be lower, as indicated by 0.888 poly-Strehl (after the gaps are reduced to 2.92mm, to bring the central line correction to the same level).
Even allowing for somewhat narrower gap - about 2mm, or so - the best combination would still be around 0.93 poly-Strehl; with no configuration limitation, the best - and the cheapest one - would be a combination using H-ZK3 (Schott N-SK5 equivalent) for the front and rear element, with 0.1mm air gaps, coming close to 0.94 poly-Strehl. It would have R3, R4 and R5 equal (absolute value) and R2 somewhat weaker, to minimize spherical aberration. For the high-end triplet, the FPL55 SD element implies BSL7 (Ohara's equivalent of the Schott N-BK7) as a near-perfect match with respect to eliminating secondary spectrum. However, due to the insufficient Abbe# differential between the two, the resulting spherochromatism limits correction of chromatism. Better result can be achieved straddling two matching glasses, one with lower RPD and smaller ABBE# Abbe# differential and the other with a higher RPD value and larger Abbe# differential. The secondary spectrum induced by each separate glass offsets one another, and if the averaged Abbe# differential is larger, the resulting spherochromatism diminishes. One such combination is with S-BAL12 (Schott N-BaK2 near equivalent) for the front element, and S-FSL5 (Schott N-FK5) for the rear. Like with BSL7, it has to be aspherized, since its spherical aberration residual at four equal inner radii is to large to be corrected by bending the mid element (and keeping the two radii pairs equal, to enable oiling). Below is shown the effect of filling air gaps with oil on the overall correction. With air gaps (top), 5th radius has a big load of spherical aberration, so quite a low level of aspherizing is needed to correct the imbalance. Secondary spectrum iz non existent, but chromatic correction on axis is limited by spherochromatism to 0.95 poly-Strehl. Filling the gaps with oil (simulated with a glass of similar refractive index as standard oils used for this purpose) changes spherical aberration load on each glass-oil surface. It is now so low at the 5th radius that no amount of aspherization would significantly change spherical aberration imbalance. It is still significantly lower than with air gaps on the 4th radius, but sufficiently high to correct the imbalance if fairly strongly aspherized - this time as oblate ellipsoid. Even with very similar lens radii to the air-gap design (633, 4x|362| and -1329mm, front to rear), due to reduced refraction at the oiled surfaces, spherochromatism is significantly reduced. The poly-Strehl rounds off to 0.99. Oiling the lens that uses BSL7 elements would have similar effect, but its spherochromatism would remain larger, with the poly-Strehl lower by about one index point (bottom, boxed).
Of course, we don't know how close are these examples to the actual designs (the CDGM triplet could be pretty close), but they illustrate that a high-end big triplet can be significantly better corrected than the run-off-the-mill variety. This doesn't mean that the latter can't have a high level of correction, and could in fact be a better bang-for-the-buck deal. Switching, for a change, from design to the real world, a forum post of one of Askar 185 owners had a double pass autocollimation test results of his unit. By his own words, the tester was not experienced nor particularly knowledgable, but the test results are usable as they are. Forum discussion was focused on spherical aberration, but it is fairly obvious that the test indicates presence of inner zone as well. In fact, the zone makes spherical aberration appear worse than what it is. According to some software, the error in green (top left) was lowering its Strehl to 0.5. Even without checking, that seems to be too pesimistic. Taking John Upton's Ronchi simulator, the default mirror setup happened to have a slightly over 1 wave P-V (middle; paraboloid at the r.o.c., which have the same error magnitude as the corresponding sphere for object at infinity, only the opposite sign, i.e. overcorrection vs. undercorrection).
It is obvious that the Askar 185 error is less than 1 wave P-V (which in a double pass would correspond to 1/2 wave actual error); it is similar to the Ronchi pattern for half as large error (botom left). That would indicate ~1/4 wave P-V in the green. It could be caused either by an error in the inner radius value, or in the gap, or both. For simplicity, will assume it was only the gap; either way, the error can be reversed by adjusting the gap. Here, reducing the first gap from 2.78 to 2.44mm (by omission, it was done on the triplet with reversed outside glasses; difference is negligible) results in just slightly over 1/4 wave P-V of overcorrection in the green line, and with it the entire LA graph leans to the right, reducing error in the red, and increasing it in the blue/violet (it is reflected in the Ronchi patterns top right; the white light pattern has some light bluish hue and yellowish accents, but doesn't show significant chromatism). Mainly as a result of the e-line error, polychromatic Strehl (photopic, 430-670nm) drops to 0.76, only three index points below the e-line Strehl. Evidently, worsening on the blue/violet end was offset by the improved red end. Some forum members expressed opinion that it was done on purpose, to have the telescope "peak in the red", but it is ludicrous to think that any manufacturer would ruin a general purpose instrument that way. It is more than anything else a quality control error. Spherical aberration also affects color of the diffraction image. Simulation below shows this system when optimally corrected, and with ~1/4 wave of overcorrection.
Overcorrection effectively shifts the blue/violet end farther away from the focus, while at the same time bringing red closer. This intensifies yellowish hue across the range of focus, including the focused Airy pattern. Out of focus patterns in the direction of focus shift become sharper, while those toward the opposite side become softer, particularly the outer ring. Note that the LA graph shows five selected wavelengths, but simulations are done with 10 wavelengths from 436nm to 707nm, even sensitivity. The zonal error widens the Ronchi bar, which means it is of the same sign, and adds to the error. Taking, very approximately, that it is centered around 0.4 radius, ~1/5 radius wide, and also ~1/4 wave P-V, the corresponding RMS wavefront error would be around 0.04. If mainly unrelated to the spherical aberration, their combined error would add as the square root of the RMS error squared, i.e. would come to 0.085 wave RMS, or the corresponding 1/3.5 wave P-V. That would also correspondingly lower polychromatic Strehl. This particular unit is unlikely to be representative of the average quality, but even half as large deviation from the design limit is still significant. After that poorly interpreted test, someone on the forum stated that such apo refractor would be no better than a standard 8-inch SCT. Well, if it was 1/2 wave P-V in the green, would have been worse. But it is an interesting comparison to make. Below is polychromatic MTF (photopic sensitivity) for perfectly made units. It shows contrast transfer for field center, 0.07° and 0.1° field.
The SCT has what appears to be a double line on axis; the upper one is its diffraction limit, due to the central
obstruction, and the lower one is its axial contrast transfer. Obviously, the effect of its spherochromatism
is very small. However, contrast transfer significantly worsens already at 0.07° off (best curved field),
primarily due to its field coma. On the other hand, the apo has practically identical contrast transfer for any
point within 0.1° field radius, significantly better than the SCT on the left half of the MTF graph, and little
better on the right half. Assuming similar fabrication quality, the apo would retain that relative contrast
advantage, resulting in a small, but not negligible, resolution advantage.
32 - Askar 140mm f/7 triplet apoOne could expect that the smaller Askar triplet is a downscaled version of its bigger brother, but the published lens configurations are different (image below). This one also has CDGM's H-FK61 ED glass as the core element, but glasses - or glass - used for the outer two elements are unknown. The first suspect, the cheapest and the best quality glass available is the Schott N-BK7 and equivalents - in this case CDGM H-K9L. It wouldn't work well alone, i.e. being used for both outer elements, because it has too small Abbe# differential vs. H-FK61 for an f/7 system (would suffer from unacceptably large higher order spherical residual), and also would produce some not negligible secondary spectrum. If it is used for the front element, the corresponding glass for the rear element has to be lanthanoid, in order to work with the published lens configuration (it looks more like a drawing than raytrace, and the lines are thick, making determinimg proportions less accurate, but any configuration that could be considered to be the actual one, or close to it, can't be significantly different from what the drawing imply). Numbers next to the radii of the published drawings represent rounded off relative radius value in units of the strongest two radii. The drawing also imply that the inner radii pairs are either equal, or nearly so. The gaps, as the separation between the middle of the radii lines, is 2.6mm. In general, standard glasses with lower index require weaker rear radius, although a few of them (H-ZK7, H-ZK5 and H-ZK10) could be close enough, requiring rear radius of 1.1m, or little less. Flipping H-K9L around to use it as a rear element would - since those two elements are of negative power, and the front element is stronger - allow for a weaker, i.e. standard glass for the front element, but the rear radius would have to be much weaker in order to have coma corrected. Replacing H-K9L with a stronger standard glass would allow for the standard glass rear element too, but would also require significantly weaker rear radius for coma correction. In all, the combination with the CDGM borosilicate crown in front, and H-LaK2A CDGM lanthanoid (Schott N-LaK9 near-equivalent) in rear, comes very close to the published configuration, and no other combination of glasses available in OSLO Edu catalog seem to fit in (limiting to inexpensive lanthanoids; H-LaK51A - a Schott N-LaK14 near-equivalent - produces similar, a bit inferior output, and at 3.9 the unit price costs more than H-LaK2A at 3.4).
Even with all wavelengths being within the "true apo" limit - except the violet g-line somewhat above, but practically not influencing the photopic Strehl value due to low eye sensitivity - the polychromatic Strehl is only 0.91. It is mostly due to the 0.96 Strehl limit in the central wavelength (although that alone would also qualify as well corrected in the apo requirements), due to the relatively large higher-order spherical residual. Was its Strehl, for example, 0.99, the poly-Strehl value would have been 0.94+. The published recipolar ray spot plot for selected wavelengths (0.44-0.7 micron) is about 33 microns in diameter, not changing significantly in size or shape up to field edge (as the recipolar blur for this system shows at 1° field radius, it has to show elongation due to the presence of field astigmatism). Axial recipolar blur for this lens is 54 microns at the best focus, and 36-37 microns at the smallest spot focus (it is common practice to present the smallest spot, rather than the best focus spot). It should be noted that the published spots are not for the objective alone, but with 1x field flattener; it could be somewhat reducing the spot size, and apparently minimizes field astigmatism. With a small reduction in the gap, the first two inner radii can also be equal, which is favorable for fabrication. Since reducing gaps also reduces the higher order spherical residual, the poly-Strehl now exceeds 0.92, with the central line limit closer to 0.97 (image below, top).
This is probably closer to the actual design, although the difference is small. Since minimizing the gaps would improve the central line limit Strehl to 0.99, and the poly-Strehl to 0.945 (bottom), inevitable question is why were the wide gaps introduced? Possible answer is that the higher-order spherical acts as an error suppressor in the violet (by curling its LA plot to the left toward top). Without it, the error in violet grows significantly larger. How much worse is this level of error in g-line than the "true apo" limit of 1/2 wave P-V? The problem with this nominal limit is that it does not specify the form of aberration. With achromats, the dominant form is defocus, and with apos it is most often spherical aberration. Plots below show how this g-line error - nearly 3/4 wave P-V of somewhat defocused spherical aberration measures up against 1/2 wave P-V of pure defocus.
While 1/2 wave of defocus has nearly twice higher Strehl and less than half as large 80% energy circle, when it comes to the final judge - the image contrast - it is not clearly ahead of 3/4 wave of spherical aberration + defocus. It has clearly higher contrast transfer up to about 0.3 frequency (3.3 times the resolution limit λ/D in radians - times 206,265 for arc seconds - or little over 1.3 Airy disc diameters line pair width), but between 0.3 and 0.5 frequency (twice the resolution limit) it is spherical aberration that has the upper hand. And if defoocus would have the same error magnitude (dashed blue), spherical aberration would have convincingly better transfer for fequencies beyond 0.2 (five times the resolution limit). The reason for this is revealed by the respective PSF simulations: 1/2 wave defocus is paying for its better energy concentration with a larger bright diffraction core, getting in the way when details become small. As a result, it will do better with dim low-contrast and bright low-contrast details, but will take back seat to spherical aberration with a dim high-contrast detail resolution. It comes back in front for bright high-contrast detail resolution, although at this error magnitude its contrast transfer is compromised by being very close to the cutoff level. This illustrates that the effect of different aberrations on contrast is more complex than the nominal indicators alone, be it the wavefront-associated or energy-associated values. It is also the form of point image that influences the final outcome. It is interesting that replacing the lanthanoid with standard crown, H-K10 (Ohara S-NSL3 near-equivalent), and flipping it to the front, would produce better corrected objective, with all four inner radii equal, and no need for wide gaps (below).
At 56 microns in diameter, the smallest blur is some 50% larger than
in the lanthanoid version, but the poly-Strehl is better, mainly
due to the lower higher-order spherical residual, i.e. the higher
central line design Strehl limit. It is quite possible that the main
criteria wasn't the overall correction, but the smallest blur size.
Chromatism-wise, measured by the photopic poly-Strehl, the lanthanoid
version is slightly better: if it would have the same 0.996 central
line Strehl, its poly-Strehl would have been 0.949. 33 - 130mm f/7 triplet: ED vs. SDAir-spaced 130mm f/7 apochromatic refractors come in two flavors: either specifying Ohara FPL53 (e.g. TS-Optics Photoline 130), or just generally ED glass (e.g. Astro-Tech AT130). It is fair to assume that the latter implies higher-dispersion low-dispersion class, like Ohara FPL51, Hoya FCD1, or CDGM FK61 (extra-dispersion and super-dispersion labels can be somewhat misleading, since these glasses have extra low dispersion). Whether it is the case, or not, with AT130, for the sake of comparison in the correction level of 130mm apo triplets with super-low and extra-low dispersion glasses it will be assumed as being using FK61 (doesn't make difference which particular glass from that class is used). When it comes to the FPL53 triplet, the question of mating glass is easy to answer: no other glass will outperform BSL7 (Schott N-BK7 equivalent), which is also the cheapest and of best quality (using BSL81, near-equivalent of Schott N-LaK21, produces practically identical result, but costs more). As shown below, this triplet easily passes the "true apo" requirement, both, with respect to the maximum error allowed in widely separated wavelengths, and in the polichromatic Strehl value (min. 0.95).
The glass combination doesn't allow for two pairs of identical inner radii, by bending the mid element. Replacing FPL53 with FK61 opens up more possibilities with respect to the mating glass. One is certainly the combination mentioned with the Askar 140mm triplet above. When scaled down to 130mm, it is right on the 0.95 poly-Strehl mark (below, top).
Another viable glass is K4A, a Schott N-ZK7 near-equivalent (2nd from top). It has more of the higher-order spherical residual, which also worsens its correction in the blue/violet. It can be remedied by using H-ZK7 (dense crown, equivalent of LZOS TK14, and close to Ohara BSM16) for the front element (3rd from top). Apparently the best straddle - combining two mating glasses, one with lower RPD value and Abbe# differential and the other with higher, so that secondary spectrum remains negligible - is with H-LaK51A (Schott N-LaK14 near-equivalent) for the front, and H-K9L (Schott N-BK7 equivalent) for the rear element (4th from top; reversing the order results in a significantly more of the higher-order spherical residual, limiting the central line Strehl to slightly over 0.95). Using the lanthanoid for both, front and rear element, results in introduction of some secondary spectrum, about f/10,000 - because even if it is the closest lanthanoid on the RPD diagram, it already has a not negligible RPD differential vs. FPL53 - but thanks to the reduced spherochromatism, the poly-Strehl clocks at 0.956. The violet g-line, however, has over 1.1 wave P-V of defocus.
The last two ED triplets are about 0.02
in the Strehl value
behind the FPL53 triplet, and the first ED triplet only slightly
more. It amounts to 0.98 Strehl degradation factor, or 0.0225
wave RMS effect - less than 1/13 wave P-V of primary spherical aberration.
It indicates that fabrication quality is probably more important
performance factor than glasses used. With the triplet using H-LaK51A
for both outside elements, contrast level at the photopic sensitivity
level would be the same as with the other ED triplets having 0.95+
poly-Strehl, but with more of violet fringing noticeable. This is,
of course, all at the design limit level. If the actual unit has,
for instance, a 1/6 wave P-V of spherical aberration worth of
correction error in the central wavelength (0.91 Strehl), the
poly-Strehl drops to 0.86-0.87 level. 34 - Pentax 75/105/125 SDHF astrograph refractorsThese fast doublets - the field flattening meniscus has negligible effect on longitudinal chromatism - generally went under the "apo" label, and were designed with astrophotography in mind. The smaller two were f/6.7, and the 125mm was f/6.4. Published prescriptions are for 1000mm focal length, so that all three had to be downscaled to their actual values. Since the original prescriptions use d-line (588nm) as the central wavelength, it is kept that way, instead of the usual e-line. Raytracing these prescriptions showed that none of the three qualifies as a "true apo", and the bigger two instruments are closer to the achromat correction level.
The main problem with fast doublets is that they have to use lanthanoids in order to avoid too much of a higher-order spherical residual due to insufficient Abbe# differential. But lanthanoids are less than perfect mating glass for extra- and super-low-dispersion glasses, with generally unfavorable dispersion in the violet. Also, the larger their Abbe# differential vs. low-dispersion glass, the larger their relative partial dispersion (RPD) differential, i.e. secondary spectrum as well. Since these doublets are pushing the envelope (for a doublet) speed-wise, it is the main part of their chromatic error. The 75mm unit comes close to 0.95 photopic Strehl, that can be considered a "true apo" entry level, only due to the very low photopic sensitivity to both violet and deep red. With the average CCD sensitivity, its poly-Strehl (in the same 430-670nm range) drops to 0.71. Error in the blue/violet could be reduced, but only at the expense of larger errors in the red - already quite large. Correction mode in the 105mm unit is similar, with the errors somewhat larger, except in the violet with disproportionally larger error. The 125mm unit has somewhat reduced error in the violet, at a price of somewhat increased error in the blue and red. Photopic poly-Strehl for this design is only marginally (less than one index point) better than for a 100mm f/12 achromat. At first, it seems illogical, since its C/F averaged error is little less than 1/2 wave P-V, vs. 1 wave in the achromat. But the LA plot, showing elements of primary spectrum (red and blue/violet on the opposite sides of the central line) gives a hint as to why. Looking at the chromatic shift curves (below) we see that the familiar parabolic curve of secondary spectrum (achromat) remains close to zero defocus for an extended range of wavelengths around the central wavelength, while that of the Pentax is similar to the typical primary spectrum curve, crossing the zero value in the central wavelength and generating defocus more quickly toward both, red and blue/violet side.
Defocus plot scale is ten times larger for the achromat, but defocus error is in inverse proportion to the focal ratio. The plot itself is not showing the actual error, since it follows shift in paraxial focus, which is not determining defocus error in the presence of significant spherochromatism (the error is determined by the location of best focus). But it shows what is it that makes the difference, and that is the pace of defocus change away from central wavelength, which is higher for the Pentax. In other words, wavelengths close to the central wavelength are more affected with the Pentax (in a smaller part, it is also due to the Pentax being designed around d-line, which has lower photopic sensitivity than e-line). In short, these astrographs are not as well corrected as the use of FPL53 glass would indicate - the larger aperture, the more so. Realistically, it is about as much as could be done with a doublet. Replacing FPL53 with fluoride (more exactly, calcium fluoride) would somewhat improve correction level, but it would still remain safely distanced from a "true apo" in the 125mm aperture. It is not because fluoride is better a glass, it is because it is higher than FPL53 on the RPM diagram, thus having less of a RPD differential vs. lanthanoids (below). Diffraction images (d-line right, polychromatic for the five wavelengths, even sensitivity, left) show some lateral color error residual remaining; it can be cancelled by making the meniscus little more strongly curved.
Keeping the same level of error in F (blue line) as in the FPL53
design, the poly-Strehl
increases to 0.863. However, it is not the best possible correction,
photopic-Strehl-wise, since reducing the error in F-line by slightly
weakening a positive lens radius, also reduces the error in red,
with the increased error in violet being near negligible due to
its very low photopic sensitivity. In the optimal mode (box at left),
photopic poly-Strehl reaches 0.90 (similar poly-Strehl improvement
would take place with optimizing the FPL53 lens, but Pentax apparently
preffered lower violet error, which becomes more important in the
CCD sensitivity realm). 35 - 100mm f/11 refractor: SD vs. EDHow much difference makes super(low)dispersion vs. extra(low)dispersion glass in a slowish refractor, such as a 100mm f/11? One established European vendor (TS Optics) offers a choice: SD doublet for 1449€, and ED doublet for 849€. Is the SD doublet substantially better than the ED, to justify the price difference? That question cannot be answered conclusively, since the glasses used are not disclosed (except that the SD glass is Ohara FPL53), but using generally available, suitable glasses, one can get a good idea of what the difference is. When it comes to the SD doublet, the choice of mating glass is rather obvious: Ohara S-BSL7, or equivalent (e.g. Schott N-BK7). No other glass is cheaper, of higher optical quality and better performing in this particular combination with FPL53. The TS Optics site states that the lens uses "two special glasses", but looking at the raytrace below (1) it can only be understood as a marketing talk. The central line design limit is 0.998, and the polychromatic Strehl (photopic, 430-670nm) design limit is 0.993 - practically perfect. The only question is how close to it come the actual units, due to fabrication limitations. Considering relatively relaxed inner radii, polychromatic Strehl in excess of 0.95 is quite possible.
The ED glass used is not specified but, at least raytracing-wise,
there is little difference between the major brands. Staying with
Ohara, its FPL51, also combined with BSL7, would produce a viable
lens with the poly-Strehl limit just short of 0.95 (2; replacing it,
for instance,
with the Chinese counterparts, H-FK61 and H-K9L, would produce
practically identical outcome). But better combination is available,
using Chinese K4A glass (Schott N-ZK7 analog). In combination
with either FK61 (shown) or FPL51, it produces output only slightly
inferior to the SD lens, but practically indistinguishable (3). There
are other viable combinations, such is
the one using Hoya glasses (4). Ohara analogs produce
a bit inferior output, and CDGM's are slightly better (their dense barium-crown
equivalent H-ZK21, is listed as fairly inexpensive at 1.8 the H-K9L price).
The conclusion seems to be that the SD
glass, in this particular case, is not necessarily significantly better than the
ED glass; at the worst, the ED lens is a 2-3 poly-Strehl index points behind,
unless is made worse than it can be, on purpose or by neglect.
Where SD glass really can make difference are the fast
apo doublets.
36 - APM Telescopes 152mm f/6 SD ApoAs per APM's good tradition, they give a good bit of specific information about the objective performance level. No glasses are specified, but there is little difference between SD (super-low-dispersion) glasses, and for this fast and big doublet the mating glass has to be on the far end of the RPM (relative partial dispersion) diagram: some short flints, and glasses containing special metals, like tantalum, niobium or lanthanum. The latter have in general similar optical properties, but those made with lanthanum are the most likely choice. The farther off from any given SD glass is the mating glass on the RPD diagram, the greater the RPD differential, i.e. the more of secondary spectrum created. In other words, lens objectives using a glass from this group as the mating element inevitably have some secondary spectrum, despite the other element being SD glass. It is a compromise between having highly corrected (i.e. with very low secondary spherical aberration residual) central wavelength, and as low secondary spectrum as possible. In this respect, the best SD glasses are fluoride (FPL51, an ED glass, is as high on the RPD as well), followed by FK61 (ED), FPL53, OK4, FCD100, FK95 and FPL55. Taking that the SD glass here is Hoya's FCD100 (FK61 would have more of a secondary spherical residual than what the plot shows), the mating glass producing output very similar to the published one is Hoya's lanthanoid LaC10 (nearly identical to CDGM's H-LaK54). It should be noted that published data have some inconsistencies: the Strehl-across-the-wavelengths plot indicates that the optimized wavelength is around 580nm, while the LA plot shows the 588nm wavelength not being minimized, and also being off its best focus significantly more than it would have been if the 580nm line has its error minimized. What is the best focus (0) on the LA graph corresponds to the best focus for ~550nm wavelength, when it is minimized. Since there is no use of optimizing for yellow-orange wavelengths for a general purpose instrument (even for the "red planet", optimizing for d-line, as opposed to e-line, results in a nearly two index points lower polychromatic Strehl, due to the shift away from peak eye sensitivity), raytrace below is for a system optimized for e-line; it results in the error for d-line only little larger than the one shown on the published LA plot.
Secondary spectrum, measured by the separation between optimized and the common F/C focus is nearly 0.12mm, or f/7600. That is more than four times less than with the standard achromat, corresponding to a 150mm f/25 achromat level. But, unlike long-focus achromat, this objective also generates significant spherochromatism. The OPD plot indicates that the F/C averaged error is little over 0.6 wave P-V, which nominally corresponds to a 100mm f/16 standard achromat level. The 0.849 polychromatic Strehl (photopic, 430-670nm), measured at the best diffraction focus (shifted 0.018mm from the e-line focus), corresponds to a 100mm f/15 achromat. While it can be regarded as a good chromatic correction, it is not as good as described on the APM site, or even by some of its users. Any possible explanation?
One of the reasons is that the violet g-line error of little over
2.5 waves P-V of the SD lens is significantly smaller than nearly
4 waves P-V in the f/15-16 achromat. By that measure, it is
comparable to a 100mm f/23-24 achromat. Since photopic sensitivity
renders the violet error nearly negligible, it has little effect
on the photopic Strehl (but becomes significant shifting toward
the nightime eye sensitivity, and more so with CCD). Another
reason is that chromatic spherical aberration (i.e. spherochromatism)
in general spreds energy less wide than defocus error, dominating
in the mid- and long-focus achromats. Encircled energy plots (bottom)
illustrate this for the F and C-line of the SD lens. While that for
the F-line is somewhat of a mixed bag, with a smaller central
maxima, but more energy around it, the C-line shows significantly
more concentrated light in a point image than defocus error of
the same magnitude (PSF simulations are normalized to 0.1 and 0.02
of the peak intensity, with all brighter areas showing uniform
white). In general, the larger error, the more is energy spread
wider with defocus vs. spherical aberration. So, in addition to less noticeable violet, the red and blue
are also less noticeable, making the view be, or appear better corrected
chromatically than in what would be the
Strehl-wise comparable achromat.
37 - Zeiss 63mm f/13.33 TelementorThis little telescope from the early 1970s that comes on an equatorial mount, was made with such attention to design and detail that probably anyone who laid an eye on it wanted to have it - I certainly did. Its objective, designated by C63/840 is a cemented doublet consisting of the crown (BK7) front element, followed by flint (SF2). It has practically identical overall correction to the standard BK7/F2 combination, except that it has lower central line corection limit: λ/44 vs. λ/12.5 wave P-V of overcorrection, which carries over to non-optimized wavelengths. Raytrace below shows it in more detail; assumed is correction mode with the blue (F) and red (C) lines' error balanced.
With the F/C error at 0.6λ P-V it compares to a 100mm f/20 standard achromat (violet g-line and deep red r-line are at that level as well). The corresponding polychromatic Strehl (photopic, 430-670nm) is 0.867 at the e-line (546nm) focus, and 0.900 at the location of best, diffraction focus, shifted 0.08mm toward the blue and red foci. Correction level is not quite as good as that of Telementor's predecessor, with AS63/840 objective, using a short-flint negative element (KZF2/BK7 combination, bottom), labeled as semi-apo. This particular combination cannot be cemented w/o aspherizing, because of unacceptably large spherical aberration residual as a result of the equal inner radii requirement. Despite being Steinheil arrangement, with the negative element in front, hence requiring stronger inner radii, its central line correction limit is still as low as λ/34 wave P-V. The corresponding poly-Strehl is 0.901 at the e-line focus, and 0.923 at the location of best, diffraction focus, shifted 0.07mm toward the blue/red. From RMS=0.24(-logS)0.5, with S being the Strehl ratio, best focus Strehl values for the two objectives correspond to 0.051λ and 0.045λ RMS wavefront error for the C and AS objective, respectively, analog to λ/5.85 and λ/6.63 wave P-V of primary spherical aberration. Plots below show how much the two differ in contrast transfer (photopic sensitivity.
The semi-apo, as the Strehl value implies, has little over 2.5% higher
average contrast transfer, and less than 1.5% higher cutoff frequency
for bright low-contrast (BLC) details. With respect to the perfect
aperture, the achromat reaches 94% of its BLC cutoff, and the semi-apo
96%. The difference is similar for the square wave contrast transfer
(top right). 38 - Zeiss 200mm f/10 APQ tripletOn the bottom of a printed list of Zeiss objectives someone added by hand data for 200mm f/10 triplet. According to the Company Seven's Zeiss page, this triplet didn't get to the APQ production line (although could have been made as a prototype). Nevertheless, it is an interesting lens - as all Zeiss lenses are - and raytracing will also show how does it compare to some new apo objectives of similar size. Company Seven states that the APQ project started back in 1979. with air-spaced objectives using calcium fluorite as one of the elements, evolving in the mid-1980s to the APQ triplet series with the gaps filled with a special oil that could accommodate for the fluorite's relatively high coefficient of expansion. While strictly talking this 200mm objective should be an oiled triplet (Q denotes "liquid" in German nomenclature, AP stands for "apochromat"), considering its size it could also be air-spaced. If oiled, it has to have one radius aspherized to minimize spherical aberration. If airspaced all-spherical, it needs to have one of the inner radii slightly altered if keeping narrow air gaps, or can have equal inner radii with somewhat wider second gap. Since there is no appreciable difference in chromatic correction between these modalities, any of them well represents the design. Here, the air-spaced triplet with wider second gap is shown. Correction mode is chosen so that the objective satisfies the technical "true apo" requirement, with the violet g-line error below 1/2 wave P-V.
Despite the handwriting stating that the RC index for this lens is 0.49, the actual secondary spectrum, defined as the separation between green and the common red/blue focus, is practically non-existent. All axial chromatism comes from spherochromatism, not from secondary spectrum. Even if the red/blue error is minimized (625.2mm inner radii), or the red and blue paraxial focus are brought together (622mm inner radii), the green focus remains practically coincident with them. Hence, it is not clear where the 0.49 value, indicating defocus blur equaling half the green Airy disc diameter - or, in this case, 0.07mm F/C defocus - comes from. As the magnified axial raytrace for red (C) and blue (F) above the LA graph show, the actual blurs are larger than half the Airy disc, and they are a consequence of spherical aberration, not defocus. If the F and C paraxial focus are brought together without adjusting for spherical aberration, the separation between common F/C focus and best green focus (nearly 1/20 wave P-V) would correspond to 0.48 RC index. But it is only an arbitrary construct, as the RC index generally is whenever it is applied to a lens with spherochromatism dominant over defocus. Polychromatic Strehl (photopic, 430-670nm) for the "true apo" mode is 0.979 (only slightly higher at the location of diffraction focus, shifted 0.01mm from the e-line focus). With the blue/red error minimized to about 1/14 wave P-V (violet g-line goes over 0.6 wave), the poly-Strehl increases to 0.985. This is, of course, the design limit. An actual unit with the central line at 0.95 instead of 0.999 Strehl - and all else equal - would come to a 0.936 poly-Strehl. For comparison, an actually produced APQ lens, 150mm f/8 (bottom), has very similar correction level, only slightly behind the 200mm f/10, as its larger relative aperture outweighs a bit the benefit from its smaller size. The higher-order spherical aberration residual, visible on the LA graph, increases error in the blue-violet, and decreases it in the red, but the effect is negligible.
This particular triplet combination uses two glasses that straddle around
fluorite on the RPD diagram: BSL7 has negative RPD differential vs. fluorite
and less of Abbe# differential, while NSL has positive RPD
differential and larger Abbe# differential. Either one alone would
produce unacceptably large secondary spectrum with fluorite (e.g. close
to 0.4 wave P-V in the case of BSL7), but of opposite sign, so that
combined they offset one another, with secondary spectrum practically
canceled out. Interestingly, BSL7 paired with FPL53 would produce a
triplet with a slightly higher poly-Strehl: 0.988.
39 - 102mm f/7 ED doublets (revisited)These attractively priced fast ED doublets come with a fit and finish similar to the high-end apo refractors. The ED element is either Ohara FPL51 (e.g. Svbony SV503), or CDGM FK61 (Astro-Tech AT102ED). Optically, these two glasses are for all practical purposes identical; the only difference can come from the quality of fabrication. No prescription was published and, to my knowledge, not even the mating glass is specified for any of these doublets. Based on what hasn't been said, it is fair to assume that the mating glass is not lanthanoid, since these have a good reputation, hence positive marketing effect. That leaves us with the crowns and, considering the price, probably those at the cheaper end. The mating glass is probably Chinese (CDGM), since if it was Japanese (Ohara, Hoya) or German (Schott) that would likely be mentioned in their marketing presentation (also, it is more likely considering the price level). The heavy crowns (ZK in the CDGM nomenclature) are not suitable since, as a transitional glass toward lanthanoids in that respect, they have significantly higher refractive index, requiring also stronger dispersion (i.e. lower Abbe#) in order to keep the secondary spherical aberration residual acceptably low - and they don't fulfill that condition. It is similar with the Barium Crown (BAK) glasses. What is left is a group of common crown glasses, most likely those from CDGM. According too the OSLO Edu catalog, they range in price from 1.6 times the K9L (Schott BK7 equivalent) for K51, to 12.6 times for K1. Price itself does not correlate with how well they perform: it is mainly result of their Abbe# differential vs. ED glass - the higher it is (i.e. the lower Abbe#), the less strongly curved inner radii, and the less of higher order spherical aberration residual. Chromatism wise, they are similar, with those with higher Abbe# differential tending to have somewhat more of chromatism, particularly in the violet. Taking a crown toward the low price end, but not the bottom - K10, equivalent of Ohara S-NSL3 and now obsolete Schott K3 - gives output shown below.
Taking default correction mode, with the blue (F-line, 486nm) and red (C-line, 656nm) errors balanced at about 0.4 wave P-V each, the violet g-line (436nm) exceeds 1.6 wave P-V. While it is far from the "true apo" limit of 1/2 wave, it is comparable to the violet error in a 100mm f/36 achromat: i.e. still low. With respect to polychromatic Strehl (photopic, 430-670nm), much more significant is the error in F and C, and the wavelengths between them and the central wavelength (e-line, 546nm). It is the main reason the Strehl clocks at 0.854 (diffraction focus, 0.014mm from the e-line focus) - not much better that the 0.818 poly-Strehl for a 100mm f/12 achromat. It is somewhat surprising, considering that the F/C P-V error is about 2.5 times lower in the ED doublet, but only as long as the central line error is not factored in. With the achromat, the design limit is practically at the Strehl value of 1, vs. ED lens with a 0.95 limit. It implies that chromatic correction is as much better with the ED lens, i.e. effectively 0.854/0.95=0.90, vs. achromat's 0.818 coming entirely from the error in non-optimized wavelengths. The central line limitation can be overcome with only moderately more expensive crowns. For instance, replacing K10 with K12 (equivalent of now obsolete Schott ZK5 and Ohara O-ZSL5, 3.6 vs. 4.7 times the K9L price) brings the poly-Strehl to 0.887, and replacing it with K8 (5 times the K9L price), takes it to 0.903. On the other hand, with the cheapest crown available, K51 (equivalent of now obsolete Hoya C12 crown), the e-line limit is 0.932, and the poly-Strehl is 0.799. All considered, it is likely that the poly-Strehl of these ED objectives is near, or at 0.90 which is probably close to what the common perception is. As an update, I run into an ad for the SV503 on the Belgian Amazon stating that the mating element is lanthanum (no specifics). Available inexpensive CDGM glasses that would work with FK61 seem to be limited to lanthanum flints, H-LaF3B and H-LaF2. With the latter having a lower price (3 vs. 3.3 times the K9L price), and similar overall correction, it is the likely choice. Raytrace below shows it having somewhat inferior chromatic correction - to expect from a glass that far at right on the RPD diagram - but nearly perfect central line correction.
It averages out a little over 0.6 wave P-V in the F and C line, which is
comparable to a 100mm f/19 achromat, and has 3.2 waves P-V error in the
violet g-line, comparable to a slightly faster achromat. Its polychromatic
Strehl design limit is 0.87, less than two index points better than the
crown combination. In other words, it's somewhat inferior chromatic correction
is more than compensated with its better central line correction, but the
difference remains relatively small. Lanthanoid
glass is more likely choice for this objective, because requires much more
relaxed inner radii, thus having significantly less stringent fabrication
and alignment tolerances.
40 - The cheapest 200mm f/7 FK61 tripletHow good is the cheapest FK61-based 200mm aperture triplet, which fits the price of a newly announced big apo by Askar? Slapping together the cheapest CDGM heavy flint (H-ZK11, equivalent to Ohara S-BSM18 and now obsolete Schott SK52) in front, H-FK61 ED glass and the cheapest CDGM crown (H-K9L, equivalent to Schott BK7) in rear, produces raytrace output shown below (it doesn't work that well in reversed order). OSLO Edu catalog lists ZK11 price same as that of K9L, which makes this triplet combination as cheap as possible. Being the cheapest, of course, doesn't qualify them as a good match. They straddle FK61 on the relative partial dispersion (RPD) diagram so that K9L is with negative RPD differential, inducing negative secondary spectrum, and ZK11 with positive RPD differential, nearly offsetting K9L. The smaller K9L Abbe# differential vs. FK61 averages out with the larger differential of ZK11, producing enough of the differential for these two glasses not to produce unacceptably high secondary spherical aberration residue.
The LA graph shows only a trace of secondary spectrum, with the colors in the visual range tightly bound together. Nearly all chromatism comes from spherochromatism, i.e. from spherical aberration increasing away from the optimized wavelength. Defocus becomes significant only in the violet which, at 1.3 waves P-V of defocused spherical aberration, nominally compares to the violet defocus error in a 100mm f/45 achromat. The red and blue are just below "diffraction limited" (0.80 Strehl), the latter being the maximum allowed for a "true apo". Polychromatic Strehl (photopic, 430-670nm) is just short of 0.91, implying that the difference vs. "true apo" (>0.95 poly-Strehl) should be detectable, but should remain relatively small. The compounded ray spot plot fits into 0.038mm circle, but 90% of polychromatic (photopic) energy fits into 0.02mm circle. For the average CCD sensitivity, the circle is nearly twice as large, with 80% of the energy contained within 0.017mm diameter circle. In all, its correction level can be envisioned by a double comparison: it is more ahead of the two bigger Pentax astrographs above, than behind a 200mm f/7 triplet that would fulfill the minimum "true apo" condition, 0.95 poly-Strehl. A bit more on the nominal equality of defocused spherical aberration (with respect to the best focus) vs. pure defocus. While they are both 1.3 wave P-V, they have different wavefront shapes and, consequently, different effects (defocus has lower RMS wavefront error, which is in general more competent, but only for low aberration levels). As shown below, the former encircles significantly more energy up to nearly three Airy disc radii from the center, after which it is defocus that encircles more energy, up to beyond 0.04mm radius. But this higher distant energy translates into a larger blur, as PSF simulations show. When normalized to their respective PSF peaks, much lower with defocus (0.0488 vs. 0.244 with defocused spherical aberration), simulations show relative intensity distribution vs. peak. But the intensities become comparable when normalized to the same value, in this case 0.1 of the intensity of aberration-free aperture; it shows the actual difference in brightness (since the defocus peak is lower than 0.1, the entire pattern is in effect darker than when normalized to its peak).
Larger defocus blur also translates into lower contrast transfer
for mid- and high frequencies, extending partly into low frequencies
(bottom). Even if defocused to its paraxial focus, when the P-V error
increases to 2.8 waves P-V, defocused spherical still forms a smaller
central blur (roughly 50% larger in diameter than at the 1.3 wave focus
location), which is also fainter than the pure defocus blur when
normalized to 0.1. All this implies that the effective
violet error for both, visual and imaging, is still significantly
smaller with defocused spherical aberration than defocus error.
In other words, the effective violet error in this 200mm f/7
triplet apo is significantly smaller than in a 100mm f/45 achromat
(or, at the same aperture level, 200mm f/90 achromat). 41 - SW Espirit 150mm f/7 "Super Apo"This objective by Sky Watcher is advertised as "Super Apo", with "virtually eliminated false color". They also specify the glasses used for it (FPL53 and two BK7 elements), which allows it to be raytraced i.e. putting exact numbers on its performance sheet, as far as the design limit is concerned. The two BK7 elements imply a NPN (negative-positive-negative) lens arrangement, since the lower index element has to be of positive power. This particular combination has too much of spherical aberration residual with all four inner radii equal to correct it by bending the middle element, so the only option - other than aspherzing - is to make one of the radii different. The color mode is, by default, the one with blue F and red C lines nearly equal in error magnitude.
The LA plot shows that secondary spectrum (i.e. color defocus) is practically eliminated, with the only form of chromatism remaining being spherochromatism. According to both, OPD plot and polychromatic Strehl (photopic, 430-670nm), the objective satisfies the "true apo" requirements (no more than 1/4 wave P-V in F and C, 1/2 wave in the violet g and deep red r line, no less than 0.95 poly-Strehl). Considering the 0.998 Strehl design limit in the central wavelength, the only contrast degradation factor is spherochromatism, reducing photopic Strehl to 0.963 (slightly defocused; 0.961 at the e-line best focus). However, with the "true apo" definition requiring the central wavelength to be corrected to at least 1/8 wave P-V (primary spherical, 0.95 Strehl), this objective would hold it as a "true apo" by the technical definition with the poly-Strehl down to 0.96x0.95=0.91. With eye sensitivity to the non-optimized wavelengths generally increasing under darker, real-life conditions, the effective (mesopic, or photopic/mesopic) poly-Strehl would certainly drop below 0.9, i.e. roughly down to 1/5 wave P-V of primary spherical aberration level. Yet, atmosphere allowing, such objective is still delivering contrasty, stunning, "color-free" views.
As a side note, spherochromatism, even when low as in this case,
results in unsightly, "bad hair" ray spot plots, significantly
larger than the Airy disc. Knowing that the ray spot plot at
1/4 wave P-V of primary spherical aberration is more than 3.5
times larger than Airy disc - as opposed to, for example,
0.8 times the Airy disc spot size for the same magnitude of defocus -
helps understand that the blur size is not a reliable indicator
of quality. Shifting focus location toward marginal rays' focus
will result in smaller ray spot plots; making the common focus
area that at about 0.866 zone minimizes the blur size, but
significantly increases the wavefront error (bottom, boxed).
As a result, the poly-Strehl drops from 0.96 to 0.82.
Yet, most
people would consider the smaller-spot modality better corrected. 42 - Askar 151PHQ Flatfield ApoThis modern-day apochromatic refractor combines a triplet objective with a separated field-flattening meniscus. Its description doesn't specify glasses, but the optical scheme supplied indicates two ED-glass elements in the triplet, hence a PNP (positive-negative-positive) lens arrangement. Since the special glass is given only as "ED", it probably belongs to the less potent group with Abbe# number around 82. There is no meaningful difference between the few of these glasses from different manufacturers, so it will be assumed it is (likely the cheapest) Chinese FK61. One of the best matching glasses for it is H-ZK3, analog to the Schott N-SK5 heavy crown. It also happened to be nearly as cheap as BK7 and analogs. For the meniscus, assumed is the cheapest and also of highest quality Chinese (CDGM) BK7 analog, H-K9L. In a configuration similar to that given by the manufacturer, they produce output shown below.
Correction level at the design limit is close to perfect, with the only exception being the violet end, slightly exceeding the "true apo" 1/2 wave P-V limit in the g-line. This is in a good part compensated by a very high correction in the deep red r-line. Also, by a small increase in the F/C-line error, the g-line error can be brought below 1/2 wave, with all other wavelengths still highly corrected (below).
The more reliable true-apo indicator, polychromatic Strehl
(photopic, 430-670nm), clocks at 0.97, only one index point
below the level with the F/C-line errors minimized, still
well above the "sensibly
perfect" minimum of 0.95. It indicates that this objective, at
their respective design limits, has a higher correction level than
the SW "Super apo" above, despite being using a cheaper, less potent special glass.
Its flat field comes as an extra bonus. As raytrace shows, in the
given prescription it is not perfectly flat, but deviation is
small, and can be still smaller after optimization.
From the designing standpoint, the simplest way to do it is
to increase meniscus thickness. It reduces already low astigmatism,
while also reducing somewhat Petzval curvature, and by that
significantly lessens already low field curvature.
For instance, making corrector 21mm thick would reduce the error (e-line)
from over 0.9 waves P-V (0.23 wave RMS) at 1° off axis to 0.36 waves
P-V (0.081 wave RMS),
i.e. close to "diffraction limited" maximum. It would require only small
changes in lens radii (R2-5 to |341|, R1 to 400, R6 t0 -1930, and R8 to
106.59mm), with the two gaps increased to 2.02mm to minimize the central
line error. Further increase in meniscus thickness would result in
relatively insignificant improvement, since astigmatism at this point is already
practically zero. 43 - TS Optics 130mm f/6.25/5 apoHow well corrected can be this fast triplet of this size? TS optics only specifies glass type for the ED element - Hoya's FCD100, practically identical to Ohara's FPL53 - but the matching glass is not too hard to guess: there is no better overall candidate from BSL7 (Hoya's equivalent of Schott BK7). No other glass is cheaper, of better quality, and offering better balanced, high correction. Below is how this combination raytraces.
Its design limit places this objective into "true apo" category, both, with respect
to the error in five widely separated wavelengths and polychromatic Strehl (photopic;
peak diffraction intensity is slightly shifted from the e-line focus).
Rectilinear ray spot plots show more clearly ray distribution for the five colors
(bottom right, somewhat magnified vs. standard plots). This apo is marketed as f/5
system, coming with a 4-element
corrector/flattener. It is not clear whether corrector does other corrections in
addition to flattening field, but it is to expect that the stand alone objective
is corrected to its limit, or nearly so. 44 - ES 102mm f/7 "Essential" triplet apo, revisitedSome more considerations on this air-spaced, NPN (negative-positive-negative) type triplet, with different possible glass combinations. It uses Hoya's FCD1 ED glass, a lower grade comparable to Ohara's FPL51. Explore Scientific site states it is a true apochromat, which "virtually eliminates chromatic aberrations". Matching glass(es) are not specified, which limits reconstruction attempt to finding out whether this kind of triplet can be a "true apo", and what is its typical correction level with available matching glasses. FCD1 has relative partial dispersion very similar to that of calcium fluorite, so it has the same matching glasses, except that due to its lower Abbe# it can't support as fast objective lenses. Several combinations with a single matching glass did not produce the true apo level which, in its wavefront error level requires F and C line to be below quarter wave, and deeper red r- and violet g-line below half a wave P-V. Better correction is achievable with two different matching glasses, the most likely candidate for one of them, considering its low price and quality, being Schott BK7 or equivalent. Pairing it with H-K7 as the rear element does produce correction that in its design limit qualifies as a true apo (below, top).
However, this Chinese crown is listed as "low availability" and doesn't have analog with other glass producers. Replacing it with H-ZK2, listed as "common", falls just short of the "true apo" 0.95 polychromatic Strehl, despite its P-V errors being within those required (middle). The reason is its higher-order spherical aberration residual, limiting its Strehl in the optimized wavelength to "only" 0.97. In other words, it does have color correction of a true apo, but its contrast transfer would lag just behind due to the slight error in the optimized, and wavelengths around it. Considering that 0.97 Strehl corresponds to a slightly more than 1/11 wave P-V of lower-order spherical aberration, hardly any actual unit with this level of color correction would qualify as a true apo. Still, putting H-ZK2 in front clears the lens of higher-order spherical residual, and it now qualifies as a true apo in its design limit (bottom). Note that the violet g-line error is slightly over 1/2 wave P-V, but because it is a mixed 4th/6th order spherical aberration form, its RMS error is lower than 0.15 wave - corresponding to 1/2 wave P-V of primary (i.e. 4th order) spherical aberration - resulting in a significantly higher Strehl value (0.52 vs. 0.39). Some other Chinese crowns would also work with H-K9L (Chinese Schott BK7 equivalent) producing similar correction level. They often have Hoya's counterpart - for instance, M-BACD12 dense barium-crown is equivalent to H-ZK2, BACD4 is equivalent to H-ZK6, etc. - but those are all listed as "unavailable", which makes Chinese glasses a very likely choice. In all, this Explore Scientific "Essential triplet" can indeed be a true apo, at least in its design limit. Virtually eliminating chromatic aberrations? Maybe in some other world. 45 - TS Optics 150mm f/8 Photoline apo doubletThis lens objective uses FPL53 with unspecified lanthanum glass. Since no graphs nor ray spot plots are supplied, the best that can be done in order to assess its level of correction is to consider available glasses and opt for what is overall most likely choice. Glass description is the same as for the TS Photoline 125 f/7.8 considered earlier, for which the bast matching lanthanum glass found was Ohara S-LaL14 (note that glass combinations using Hoya FCD100 and lanthanum, like Astro-Tech 150EDL, are practically identical with respect to the end result). This time other lanthanum and common glasses will be included, in order to get better picture of what the alternatives are. Also, since most lanthanum glasses from Ohara and Schott seem to be of low availability, or unavailable (similar with Hoya), the most likely actual glass is Chinese (CDGM). The equivalent to S-LaL14 here is H-LaK51A. In chosing a good match for FPL53 there is several factors to consider: 1-the relative partial dispersion (RPD) differential, determining the magnitude of secondary spectrum, 2- sufficient Abbe# (dispersion) differential, needed to avoid too strong inner radii (i.e. too much of higher order spherical residual), 3-cost, 4-availability and 5-chemical durability. Section of RPD graph below shows position of FPL53 vs. potential matching glasses: ideally, RPD differential should be near zero, i.e. the line connecting such glass with FPL53 should be near horizontal. There is lanthanum with near-zero RPD differential, H-LaK4L (near equivalent to Ohara S-BSM81) but it has insufficient Abbe# differential, resuting in unacceptably high higher-order spherical aberration residual. Moving toward the higher Abbe# differential glasses, however, increases RPD differential, i.e. secondary spectrum; secondary spectrum is proportional to the ratio RPD vs. Abbe# differential, and going left to right that ratio increases, i.e. RPD differential grows faster (in effect, secondary spectrum increases with the inclination of imaginary line connecting two glasses, as illustrated). In general, crown glasses are the closest, followed by heavy (or dense) crowns and lanthanum crowns, with lanthanum flints having the largest Abbe# differential, but also the largest RPD differential (relative to FPL53; FPL55 is somewhat lower on the RPD diagram, hence so much worse a match to the same glasses, CDGM H-FK95 is in between, Hoya FCD100 and LZOS OK4 are nearly the same as FPL53, CDGM FK61 is higher, and fluorite is the highest - together with FPL51 - at about 0.456 level, hence matching better with the more distant glasses on the diagram).
Longitudinal aberration (LA) graphs below show how correction level changes going from the glasses closest to FPL53 to those farther away. Included are, for comparison purposes, some crowns (K) and barium crown (BaK), heavy crowns (ZK) and a short flint. Overall design limit is indicated by the e-line and polychromatic (430-670 photopic) Strehl numbers. While there are other glasses too, they should fit fairly well into the picture outlined by these 15.
The best overall match is H-LaK51A, together
with H-LaK7A. The OPD plots show that they are not quite at the level of a "true apo",
which agrees with the polychromatic Strehl value. The only "true apo" combination would
be with the Schott N-KzFS2 short flint, but this glass is, according to OSLO Edu,
unavailable. It is also generally avoided due to its low stain, alkali and phosphate
resistance (similar short flint is available from Hikari, but its correction level
with FPL53 is somewhat lower, producing 0.943 polychromatic Strehl).
Chemical glass inadequacies with respect to exposure can be remedied with protective
coating, but those with respect to the fabrication process effectively prevent its use.
46 - Takahashi TSC225: 225mm f/12 Schmidt-CassegrainTSC225 was in production only for a few years, at the end of 1980s and beginning of 1990s. Widely seen as the best commercial SCT ever made (noting that it earned it back then when other major brands were of inconsistent, and generally lower quality than today) this system doesn't have published prescription, but what is known is sufficient to reconstruct its design close enough to the original that there is no appreciable difference in the output. The primary is around f/3 - which makes it comparable to the larger Maksutov-Cassegrains in that respect - with the final focal ratio of f/12. Assuming back focal length around 200mm, everything falls together as shown below. Central obstruction is 29%, with the minimum secondary size little below 26% of the aperture diameter.
Quality field is limited by coma, which is 40% lower than in a 200mm f/2/10 SCT angularly.
For the same linear field, it is 2.3 times lower, or at
the level of an f/8 paraboloid. For the same angular field, coma is 42% lower.
Spherochromatism is more than four times lower than in the
standard 8-inch SCT, practically non existent (curve on the corrector is as much shallower,
which makes it significantly easier to make accurately). If made coma-free, it has more
astigmatism and stronger field curvature, as well as about a third more of spherochromatism,
the consequence of the deeper aspheric profile on the corrector needed to compensate for making
secondary aspheric.
Secondary conic needed to correct coma is stronger than in an f/2/10 SCT, due to the lower
secondary magnification (i.e. weaker and smaller secondary). In all, optically, an f/3/12 SCT
is in every respect superior to f/2/10 SCT, with its lower sensitivity to miscollimation adding
to its easier fabrication. Its only disadvantage is about 50% longer tube.
47 - Nikon 100mm f/12 apo doubletDespite it not being in production for decades, this refractor still maintains reputation of a top-class instrument. There is no published prescription, and glass used for its ED element is Nikon's proprietary glass, described as "very similar to fluorite". However, Nikon patent documentation from the early 1970s gives ED glass specifications nearly identical to Ohara FPL51 (before Nikon developed their own ED glass, they used Schott FK51, which has somewhat different - higher - dispersion, indicating that the ED glass from the patent is Nikon's own). The matching glass is described by Nikon as being "high refraction low dispersion" which generally fits lanthanoids. Based on that, it is likely that the correction level of this refractor can be closely approximated using FPL51 and appropriate lanthanum glass. Image below shows how it changes with the choice of lanthanum glass.
The first combination is with one of the two lanthanum glasses from the same patent (top), whose refractive index and dispersion correspond to now obsolete Ohara LaL8 (LaL=low-index lanthanum glass, LaM=medium and LaH=high index lanthanum glass, with the dispersion generally increasing in strength with the index). It has superb color correction, except for the violet end, which does not satisfy the "true apo" requirement of less than 1/2 wave P-V in the g-line (436nm). However, its limit to polychromatic Strehl - more relevant, direct indicator when it comes to contrast transfer - is comfortably within the true apo zone, at 0.978 (photopic, 430-670nm; top number under "PSF" is the e-line Strehl. How stringent is this requirement for the violet can be illustrated with the fact that nearly 3/4 P-V of defocus in the g-line corresponds to a 100mm f/80 achromat - and it is still not good enough for the "true apo". The only way to improve correction in the violet (and to a smaller extent overall chromatic correction) is to use lanthanum glass with lower index/dispersion, but it comes at a price of increasing higher order spherical aberration residual, due to the more strongly curved inner radii required. With a moderately weaker lanthanoid, such as LaL14, the violet can be brought within the "true apo" limit, with the overall color correction improved to 0.985 not due to the smaller error in the g-line (which has a microscopically low photopic sensitivity of 0.012), but due to somewhat lower error toward F (486nm) and C (656nm) lines. Going to the weakest lanthanoids, like Ohara BSM81, further improves correction in the violet, but at a price of the central line Strehl lowered to 0.966 due to increase in the higher-order spherical aberration residual (since that affects all wavelength for which the eye is highly sensitive). Somewhat better correction is possible with heavy (dense) crown, like Ohara BaL41 (equivalent to Schott SK11), which due to its lower index vs. Abbe# requires less of a differential between the two inner radii, hence generating less of the higher-order spherical aberration residual (nearly identical correction is possible with lanthanoids like LaL7). While all of these examples are within the "true apo" poly-Strehl zone, a glass like LaL14 is the most likely choice, minimizing error in the violet without compromising the central line correction. In practical terms, the radii are still relatively weak, requiring lower fabrication and alignment tolerances. FWIW, if instead of its own ED glass Nikon used Schott FK51, combined with BSM81, this objective would have probably the highest possible correction (below).
Due to FK51 having somewhat higher Abbe# (i.e. weaker dispersion) than FPL51, the inner radii are more
relaxed, allowing for a nearly 0.99 Strehl in the optimized wavelength. The polychromatic Strehl is 0.987,
implying 0.997 Strehl degradation factor due to chromatism - practically none. That said, one needs to
keep in mind that those numbers relate to the photopic eye sensitivity, effectively insensitive toward
either end of the visual spectrum. Night time observing expands eye sensitivity toward either end of the
visual spectrum, and particularly toward blue/violet. This is why chromatic correction needs to meet
such a stringent requirement
for a "true apo", even for a primarily visual instrument such as this Nikon refractor. Still, with 0.92+
Strehl in the g-line, even with mesopic eye sensitivity no color error would be noticeable, more so with
spherochromatism, which is for the same error magnitude much less colorful than
secondary spectrum.
48 - One and only 12" f/12.5 Maksutov-CassegrainThis telescope was designed by Roland Christen, had optics made by Intes, with the mechanical part taken care of by Astro-Physics. Even if it is a single unit, made for Roland Christen personally, it is still a commercial telescope, simply because is neither ATM, nor professional (observatory). There is no published prescription, but its optical tube data imply ~f/3.5 primary mirror, and its secondary is separated from the rear corrector surface (Rumak type); with 29% central obstruction (28.8%, if 0.2% matter), give all information needed to reconstruct this system as close to the actual one to make the difference negligible. The only unknown before raytracing was would such system benefit from aspherizing. The answer is: no.
With f/3.5 primary and secondary separation of 800mm, there is over 100mm left for tube extension past primary and secondary surface, which is about right. Minimum secondary size is slightly over 27%, which barely fits into the published total obstruction size, indicating a minimum size secondary. The field edge illumination would remain practically unaffected for visual use, and acceptable for imaging (for instance, with 42mm clear aperture at the secondary, vignetting at that location for 0.35° beam would be 10%, likely less than at the rear end of the baffle tube, hence a non-factor).
Raytrace shows that this system is free of both, coma and astigmatism (the latter is about 1/10 wave
P-V at the field edge), with the central line correction limit at 0.982 Strehl (equivalent of
1/16.5 wave P-V of primary spherical aberration), set by the higher-order spherical aberration residual.
Since the purpose of aspherizing (usually the primary) is to reduce error in the central wavelength,
or to reduce/minimize coma - or both - there is no gain in aspherizing this system. In fact, aspherizing
the primary would inevitably induce coma, and the system wouldn't be coma-free anymore. The central line
error could be somewhat reduced with a (significantly) thicker corrector, but it would also increase
lateral color error. Longitudinal chromatism is practically non-existent. In fact, I don't
remember seeing polychromatic Strehl (photopic, 430-670nm) higher - even ever slightly, like here - than the
optimized line Strehl (which indicates that some of the non-optimized colors actually are better
corrected than the optimized one, even if the difference is very small). Best field curvature is quite
moderate, inconsequential for visual use. Practically, this system's correction level is limited only by the
accuracy of fabrication.
49 - Lichtenkneker 190mm f/4 Schmidt-Cassegrain flat-field cameraThis camera, in production decades ago by Lichtenknecker Optics, Belgium, is still used by some amateurs, and can be found sometimes on the used market. It is a flat field aplanatic anastigmat, in its basic configuration similar to the non-compact Baker-Schmidt camera, but unlike it having aspherized secondary, not primary mirror. Also, it uses internal stop, which does not influence optical output. It is positioned so that the corrector and primary mirror are approximately identical in diameter, and also has baffling effect. Another peculiarity of this system is a curved Schmidt corrector which, again, does not differ in its optical output from the flat form, but helps aleviate unwanted reflections. There is no published prescription, only system drawings and description. Based on the tube length for this particular instrument (just over 1m), the primary is about f/2, and the rest of parameters are determined by the known properties of the system. While not the exact replica of the original design, it is close enough to make differences in the output negligible. Field size was referrenced to according to the size of 24x36mm film frame, i.e. with 21.6mm semi-diagonal. Minimum secondary size is 45% of the primary's diameter, and the obstruction is taken as 50% (for a full illumination of the very corner it would have to be somewhat larger).
At 1.6° off axis, astigmatism is less than 0.01mm, translating to 1/7 wave P-V. With traces of residual coma (it can't be completely cancelled because the higher-order is large enough, and it doesn't offset perfectly with the lower-order form), the e-line Strehl is still as high as 0.98+. Chromatic correction is nearly perfect (as a camera, it uses wider spectral range than the one shown, but correction remains impecable: at 400nm the P-V error is still no larger than 0.3 (0.067 wave RMS), and less than 1/10 (0.026 wave RMS) at 900nm. If the effective area of the secondary is limited by 50% linear obstruction, vignetting in the very corner is 13.3% (as shown with the transmission map of the aperture stop, total vignetting is 35%, with 25% being caused by central obstruction). Correction wise, this system does not offer advantage over the flat-plate design, and removing internal stop would actually improve off axis correction a bit, but its practical benefits are reduced level of unwanted reflections from the corrector and probably better baffling. It is not as well corrected as an f/4 Schmidt camera of the same aperture, and it is even little longer, but the difference is not practically important, and the Lichtenkneker's system offers the advantage of the flat field. It can cover larger fields than the one determined by the 12x18mm film frame: at 2° off axis its e-line error in this particular design is still only 0.024 wave RMS, and 0.061 at 3°, well within "diffraction limited". However, much larger field would also require significantly larger secondary, in order to avoid outer field vignetting (as diffraction images illustrate, even as low as 13% vignetting already causes visible elongation of the diffraction pattern, consequence of the effective aperture shape becoming ellipsoidal). As mentioned, bending corrector does not affect its optical output. With very mildly bent corector, the rear radius is given as a differential of the front radius and the flat corrector radius factor, i.e. 1/R2=1/R1+1/Rc. Since the flat corrector radius has negative sign (here, Rc=-122,000mm for the rear side, opposite sign for the front), R2 is somewhat weaker, but as the corrector becomes more significantly bent, due to increasing optical powers of its surfaces, differential between R1 and R2 diminishes, until they equilize (here, for R1~800mm), and after that R2 becomes increasingly stronger than R1. It is possible that the actual unit has identical corrector radii, more so if it also works well for the primary purpose of bending, which is minimizing unwanted reflections. In comparison with the Baker-Schmidt with identical mirror radii and separation, Lichtenkneker is slightly longer, but has somewhat smaller width due to its smaller primary mirror. Due to its stop placed closer to the primary, it also needs smaller secondary for fully illuminated field.
Correction wise, the two systems require nearly identical corrector profile depth (w/neutral zone at 70.7%
radial height, for minimized spherochromatism), so their spherochromatism is
practically identical. Due to its spherical secondary, astigmatism in the Baker-Schmidt practically vanishes,
with the remaining off axis
aberration being oblique spherical (it can be made nearly symmetrical vertically by moving corrector about
0.5mm closer). Another small advantage of aspherizing the primary is minimized higher-order coma, resulting
in a cleaner ray spot plot (the wavefront error is also significantly lower numerically - 0.01 vs. 0.018 wave
RMS, but of no practical significance at this focal ratio and aperture). In comparison with an f/4 Schmidt
camera of the same aperture, Lichtenkneker is inferior correction-wise, but the Schmidt would be very
impractical due to its length. For the same tube length, the Schmidt would need to be about f/2.5, requiring
about 20% stronger corrector than the Lichtenkneker, hence with about as much more of spherochromatism. For
the same angular field, the Schmidt would have practically zero aberrations in optimized wavelength, and
for the same linear field
it would fall between the Lichtenkneker and Baker-Schmidt. But unlike these two, it would require either
field flattener, or curved detector surface (-475mm radius, i.e. convex toward mirror).
50 - Levenhuk Ra R80 ED DoubletThis doublet uses the same glass combination as earlier raytraced Omegon 110mm f/6 ED doublet: Ohara FPL53 and NBM51 short flint. Does it being smaller, and somewhat slower - 500 f.l. i.e. f/6.25 - produces appreciable better correction level? Assuming again the positive element in front, allowing for significantly weaker inner radii, hence less stringent fabrication/alignment tolerances, in addition to 31% lower higher-order spherical aberration residual, raytrace shows that to be the case.
Design limit in the optimized line is 0.99+ Strehl, but the blue F- and red C-line, averaging 1/2 wave P-V, are significantly below "diffraction limited" (0.80 Strehl). Still, being at the level of a 100mm f/24 achromat implies very good overall correction of chromatism, reflected in the 0.91 polychromatic Strehl - significantly better than the 0.81 Strehl of the Omegon. If Schott's near-equivalent of NBM51 (N-KZFS4) was used, correction would have been better, more than negligibly so, at the level of a 100mm f/27 achromat (0.921 polychromatic Strehl). The longitudinal aberration plot clearly shows presence of secondary spectrum, which is a consequence of the mismatch in the RPD values for the two glasses. However, due to the fast focal ratio spherochromatism is also present, so that the wavefront errors in F- and C-line are a mix of defocus and spherical aberration (the blue line is left slightly better corrected, because the error increases much facter toward violet than deep red). The wavefront shapes indicate that defocus is dominant in the blue, while a peculiar shape in the red, with the error increasing nearly linearly toward the edge, is somewhat puzzling with respect to which aberration form - if any - dominates. Both, P-V and RMS values for the two wavelengths are of similar magnitude, but the Strehl value indicates there could be more of a difference in the actual effect. Since the Strehl itself is less reliable at this error magnitude, the only way to find out is there a difference in the actual effect between the blue and red line is to look into energy distribution, PSF and MTF. Encircled energy plot shows that the F-line has significantly better concentrated energy than C-line. The PSF simulations confirm that defocus is dominant in the blue, while in the red it is spherical aberration, with presence of defocus (all simulations are normalized to 0.1 of the peak intensity, in order to show more clearly the aberration-free pattern). Despite the F-line having only slightly smaller nominal error - 0.47 wave P-V and 0.127 wave RMS vs. 0.54 and 0.148, respectively - the actual energy distribution and ensuing error are disproportionally larger for the red line, due to its particular wavefront shape, i.e. aberration mix. The corresponding ray spot plots are also very interesting: the F-line spot is significantly larger than its Airy disc, appearing more as defocused spherical aberration, than defocus. The C-line spot is just slightly larger than the Airy disc, with rays most densely concentrated within a narrow ring bound around Airy disc line (more obvious on the magnified spot below, with a higher ray density). Peculiar wavefront - peculiar ray spot plot. But it is another illustration of the spot size vs. Airy disc being unreliable indicator of the magnitude of aberration, more so at moderate-to-low aberration levels.
The difference in energy distribution carries over to the diffraction MTF, which shows that the blue causes significantly less effect on contrast transfer than the red (somewhat surprisingly, pure defocus has better contrast transfer than pure spherical near cutoff, which should be caused by MTF "object" being not a single pair of lines, but a continuum of lines, with the energy of underlying diffraction patterns overlapping). The PSF plots (bottom right) are only for 0.15 wave RMS of pure defocus and primary spherical aberration, with aberration-free plot, to illustrate the basic difference in energy distribution. All this shows that small nominal differences in the wavefront error may not reflect the actual difference in the effect on image quality, when a mix of aberrations is present. And that is generally the case with fast apo objectives. How does 1/2 wave P-V of mixed aberrations in F and C measure up against 1/2 wave of pure defocus (slower achromats), or either vs. 1/2 wave of pure primary spherical (some apo objectives) is only partly indicated here, but the general rule seems to be that the same nominal error still allows for potentially significant differences in the actual effect. If a similar exercise is done with the violet g-line, for which the wavefront shape indicates nearly pure defocus, it shows that nearly 2.5 waves P-V of spherical aberration differs more in its appearance, than in the effect (at left is the actual g-line error in this objective, and at right nearly identical wavefront error of primary spherical aberration). That generally should hold for large magnitude aberrations.
PSF shows that spherical aberration has significantly higher Strehl, but lags behind defocus when it comes to
encircled energy. Unlike defocus, it has some low contrast transfer over mid- and high-MTF frequencies,
but the range of significant contrast transfer is nearly identical for both. Note that the simulated
PSF patterns are by default normalized to the peak pattern intensity; to make brightness of the extended
areas comparable, they should have identical normalization (spherical aberration PSF at right vs. defocus PSF).
PSF for the optimized wavelength (0.546μm) is shown normalized to the peak intensity (1, top), and to
0.1 (bottom) to bring out its pattern more clearly.
51 - FPL53 doublet, or FPL51 triplet?Talking about f/7 refractor (believe it was 115mm aperture) different forum posters stated that they would rather have an FPL53 doublet than FPL51 triplet. Is that opinion well founded? Among the refractors analyzed above there is a FPL53 doublet not even coming close to what is considered to be "apo" level. How well corected that fast FPL53 doublet can be? The answer is within the frame described recently (#45). There is no great matching glass for FPL53 in general, unless a lens is slow enough that it can use a few suitable glasses relatively close to it on the relative partial dispersion (RPD) diagram. An f/7 is well outside that range. Out of the two best choices for an 150mm f/8 FPL53 objective described above, the f/7 focal ratio is too fast for H-LaK51A, which would have ~0.95 Strehl design limit in the optimized wavelength, but H-LaK7A would take it well. Raytrace below shows how it would perform in an FPL53 f/7 doublet, and FPL51 f/7 triplet, both with 130mm aperture diameter. All designs are coma-free, and with similar levels of astigmatism, so the raytrace is focused on the axial correction level.
Except for having marginally higher error in the violet g-line, the triplet is better corrected, and have higher polychromatic Strehl (photopic, 430-670nm). Its advantage over the doublet is relatively small, but not negligible. More relaxed inner radii allow for more relaxed fabrication and alignment tollerances, which should more than compensate for having an extra element with respect to its actual performance. As mentioned under #45, the best match for FPL53 with mid-fast and fast objectives is Schott N-KzFS2, a short flint not suitable for fabrication due to its chemical sensitivities (things may be changing, because lately we saw use of another short flint, Ohara S-NBM51, near-equivalent of the Schott N-KzFS4, in some fast objectives). Raytrace below illustrates how well it works here, with FPL53 doublet and FPL51 triplet.
Again, it is immediately noticeable that the FPL51 triplet has better correction than FPL53 doublet. Both objectives satisfy the minimum 0.95 polychromatic Streh criterion for the "true apo", but neither one satisfies the less than 1/2 wave P-V formal requirement in the violet g-line. Considering that the violet error in the doublet is at the level of a 100mm f/58 achromat, and f/72 for the triplet, its effect is visually negligible. Another advantage of any triplet is that it can combine two glasses with RPD differentials that nearly offset each other, widening range of usable glasses and potentially making possible to achieve higher correction levels. One example is shown below, using H-K9L (CDGM equivalent of the Schott BK7), which have a negative RPD differential vs. FPL53, and insufficient Abbe# differential for this fast a system, with H-ZK11 dense (or heavy) crown, analog to Ohara S-BSM18, with a positive RPD differential and ample Abbe# differential. The two average out to a negligible RPD differential vs FPL53, hence negligible secondary spectrum, and sufficient Abbe# differential. The combination is the cheapest possible, with ZK11 being listed at the same price as K9L.
This objective is about as good as FPL53 doublet with KzFS2, and better than the best possible combination using a viable matching glass. Some other, more or less similar combinations could be put together in an FPL51 triplet, making its choice of glasses significantly wider than for FPL53 doublet. In all, this brief comparison shows that there is no realistic basis to favor FPL53 doublet over FPL51 triplet. In fact, the latter has a small, but consistent advantage, even if inexpensive matching glasses are used. FPL53 has significantly higher Abbe# than FPL51, but that is more than compensated by a triplet allowing for more relaxed inner radii than a doublet. And, in the end, actual correction is not determined by any one glass alone, but by both - or all three - together. An interesting, a bit puzzling detail with the raytrace output is that the P-V errors in the violet g-line are roughly similar with all systems, unlike the corresponding Strehl values that vary in a range of nearly 1:4. Taking a closer look of the first four systems, shows that the main discriminating factor is a shape of the wavefront. Pure defocus has more detrimental effect than defocus mixed with spherical aberration, and the reason is rather obvious: spherical aberration widens the mid-wavefront area staying relatively close to the line of zero deviation, while defocus moves away of it immediately, after the very center, increasing the error exponentially toward the edge.
All PSF simulations are normalized to the PSF peak, i.e. those that have higher Strehl value are
shown correspondingly
dimmer than what they are nominally. The actual brightness is relatively unimportant to the eye, which
due to its nearly logarithmic
response to light intensity will detect little difference in brightness of the central maxima from one system
to another, but will
see surrounding energy much brighter than what its nominal brightness imply,
relative to the central maxima. Encircled
energy plots show that even the two systems with a higher, nearly equal Strehl values, differ considerably
in their 80% encircled energy radius. That also shows that the Strehl becomes less reliable indicator at this
P-V wavefront error magnitude, although less so than the nominal P-V wavefront error itself.
52 - APM LZOS 510mm f/12.7 apo tripletRefractor of this size - over 6m long - is certainly an observatory instrument, but it is still within amateur enthusiasts' daydreaming - or, rather, nightdreaming - domain. With optics made by LZOS, how well corrected this large refractor can be? There is no published prescription, but with just a few LZOS glasses that can be the potential match to their only ED glass, OK4, it is not hard to find that winning combination. It is K8/OK4/K8, with the K8 crown being a LZOS near-equivalent to Schott BK7. There is no glass less expensive and, at the same time, of better quality - particularly in such large diameters - on top of best correction level it provides with OK4 (which is close to so called "super" extra-low-dispersion glasses, like FPL53, but not quite there). Raytrace below shows correction level of this triplet (considering large diameter, lenses are probably somewhat thicker, but it doesn't affect correction level).
Axial chromatic correction easily meets the "true apo" criteria, both, with respect to wavefront error for five widely separated wavelengths, and the 0.98 polychromatic Strehl. It is slightly F/C unbalanced, but making them nearly even wouldn't have appreciable effect, since small improvement in the blue would come at a cost of small worsening in the red and violet. Field correction is impecable over best image surface (-2000mm radius), but field curvature is mild enough to allow the edge point be safely within "diffraction limited" on flat field.
It is a bit puzzling why f/12.7, since even at f/10 such triplet would still be nearly meeting "true
apo" requirements, and at f/11 would be safely within them. This triplet was made as a special, private order,
and that little extra correction was, apparently, deemed as being worth the extra length by the customer.
53 - Skywacher HAC125DX 125mm f/2 minigraphThis small, fast astrograph is marketed by the Skywatcher as being "Honders Advanced Catadioptric optical design". The basic form of it consists of a positive front lens, catadioptric element (Mangin mirror) and a field lens. Optical material used is quoted as borosilicate glass, central obstruction is 42.5% (linear) and image circle diameter is 16mm. No other information about the design is given, including any specifics with respect to its correction level. Published optical scheme on some vendors' sites shows what should be the actual system configuration. Since no prescription is published, this is where one can start for getting an idea on the correction level of this instrument. The published scheme is shown below (top left), and used to determine approximate radii of the optical elements.However, when put through raytrace (top right, with the corresponding prescription below at left), it is not viable. The problem is not that it focuses before the field lens; the radii are approximate, so it could be causing it, although it would exceed expected error margin in measuring the radii. For one, the front lens of such power would produce significantly more steeply converging cone than what the scheme shows. But rays may have been drawn only for illustration purposes, and the elements do correspond to the actual design? That doesn't work either, since when making the final focus form at about 30mm behind the field lens by weakening reflecting surface radius to 510mm (the simplest way to get to the supposed configuration), the excessively strong field lens not only producess unacceptably large lateral color error, but also generates strong Petzval surface. Such surface can be made flat only with introduction of astigmatism of opposite sign, but the outer field correction would be compromised. Specifically, the Petzval coefficient of 0.01mm (PTZ3, for 1.8° field radius), means that the radius of defocused spot due to image curvature is 0.01mm or, in this case, blur equaling 7.5 Airy disc diameters. Since the correcting Petzval requires longitudinal astigmatism to be equal to that of the longitudinal defocus due to Petzval curvature, and for any given longitudinal aberration value the defocus blur is twice larger than that for astigmatism, it implies astigmatic blur 3.75 times the Airy disc diameter. Since it is easy to make correction much better, the published optical scheme can't be assumed to be accurate. But the overall arrangement can serve as a basis for determining what is achievable with this design. It is illustrated with three arrangements, conforming to the given element separations and thicknesses, but with the radii altered so that a well corrected system is achieved.
Correction of longitudinal chromatism sets the requirement for relative powers of the front lens vs. Mangin mirror, with the field lens mainly affecting lateral color. Any front lens power can be mached with the corresponding Mangin mirror power in that respect, but spherical aberration in an all-spherical arrangement will be corrected only in a narrow range of powers. In this case, with given element separations and thickness, it requires front Mangin mirror radius of 320-330mm, and the rear radius as determined with the requirement of back focus distance (#1). That is significantly more relaxed than what the optical scheme indicates. This level of powers still leaves the Petzval curvature - i.e. astigmatism needed to flatten the field - significant, barely acceptable. Flat astigmatic surface is generally preferred to the astigmatism-free curved surface, as in the system shown (astigmatism is modeled by reshaping the field lens). Once longitudinal chromatism and spherical aberration are corrected, coma is corrected by reshaping the front lens, with minor adjustments to other radii in order to maintain overall correction near-optimal. The field lens has a role of balancing both, lateral color and Petzval curvature, with both requiring it to be significantly weaker than what the optical scheme implies. As a result, the system is somewhat slower, at ~f/2.2; an f/2 would have to be shorter. However, correction level difference between the two is near-negligible. If the front Mangin mirror surface radius is to be kept close to the one shown on the scheme, one surface has to be aspherized in order to control spherical aberration (#2). Best choice for that is the fron't lens' surface, since it does not introduce other aberrations. Field correction of this arrangement is significantly better. The conic is rather strong, at 3.8, but it is a function of the Mangin mirror front radius value. The closer radius to the one allowing for all-spherical design, the lower conic is needed; as the radius becomes weaker than the one needed for all-spherical design, needed asphere shifts from oblate elipsoid to prolate ellisoid, and through paraboloid to hyperboloid. With relatively minor deviations from the published scheme, significantly better correction can be achieved with all-spherical arrangement. Making the field lens thinner, and having the final image form at ~25mm behind it, allows strenghtening of the field lens, which significantly lessens Petzval curvature, hence also astigmatism needed to flatten the field (#3). Further reduction in Petzval curvature to a practical zero is possible by increasing somewhat the first two elements' separation. It weakens the blue/violet dispersion, allowing for strengthening of the field lens, i.e. further reduction of Petzval curvature. However, there is no practical gain from it, since the correction level is already excellent. In all, this simple design is capable of producing well-corrected field of this diameter, with the actal design most likely being somewhere between acceptable and excellent in that respect. As an illustration of the difference between a curved, zero-astigmatism field, and one flattened by introduction of astigmatism, raytrace below shows the #1 (all-spherical) arrangement from above as already presented, with a flat astigmatic field (A), with astigmatism cancelled and the remaining non-zero Petzval curvature (B), and with astigmatism partly reduced and somewhat defocused (C). Astigmatism is changed by reshaping the field lens, with minor adjustments to other radii in order to keep the overall correction intact.
The astigmatism-free, curved image has larger wavefront error, although not nearly as much as indicated
with the blur size (for the same RMS wavefront error, defocus blur is larger by a factor of 20.5).
Note that a residual of some other aberrations are are also present, hence it does not correspond to
the pure astigmatism vs. defocus picture, but it is close to it. Diffraction image simulations are
proportional to the Airy disc diameter (they show nominal intensity, hence differ from the visual image).
The partial astigmatism reduction (C) results in a lower P-V/RMS error, with the diffraction image
mainly preserving desirable shape (i.e. not becoming too elongated). This is not consistent with pure
astigmatism and defocus, where going from best astigmatic focus toward either line focus the RMS
wavefront error steadily increases. What is causing this particular reduction here is a presence of higher-order
aberrations, mainly quatrefoil, which to some extent mimics primary astigmatism and, if of opposite sign,
combined with defocus, makes it smaller. The encircled energy graph confirms what diffraction images
suggest, i.e. that the flat - or nearly so - astigmatic field has significantly better concentration of
energy, with the 80% encircled energy radius almost twice (0.54) smaller. That correspondingly affects both,
contrast transfer and resolution limit.
54 - Omegon Pro APO AP 85/510 Triplet EDThis small, fast apo is described as "high-quality, true-color, for first-class astrophotoraphy and observation" and alike. Its lens objective is made in Japan, a NPN (negative-positive-negative) triplet with the middle ED element being Hoya's FCD100. The mating glass shouldn't be much of a mistery, with the Schott BK7 and near-equivalents being among the best matches for this class of ED glasses. They are also the cheapest, and highest quality glass. Raytrace below shows lens using BK7, but the correction is only slighly worse - or, rather, less good - with the Hoya's BK7 equivalent, BSC7.
The g(436nm) to r(707nm) Strehl values show that this objective in its design limit comfortably passes the "true apo" requirements. Polychromatic Strehl (430-670nm, photopic) is 0.9685 with BK7, and 0.9678 with BSC7. The two aberrations that are not negligible are field curvature and astigmatism. Astigmatism is strong enough to start forming cross-like pattern at 9mm off axis. Its size is little over 0.01mm, or ~4.5 arc seconds. In a 10mm ultrawide eyepiece (80-90° TFOV), which has ~9mm field stop radius, it is about 3.5 arc minutes, still near point-like for most people. Polychromatic diffraction image (even sensitivity) indicates vertical elongation at 9mm off, but it is less noticeable with 10 wavelengths in the same range (smaller box). Omegon offers dedicated 3-lens 0.92x reducer/field flattener, that goes under "field corrector", which may indicate that astigmatism is reduced as well. As an illustration, a 3-element 0.78x reducer/corrector below shows two scenarios: (1) astigmatism practically eliminated, with some field curvature due to non-zero Petzval remaining (top), and (2) field nearly flattened with introduction of astigmatism (bottom).
Correction difference between the two is greater than what the blur sizes imply, and favor flat astigmatic surface.
All it requires is making the rear element more strongly curved. Field correction also changes significantly
with the focus plane: if it is the one containing best focus on axis (solid-line astigmatic plot), off axis
correction is lower, and with
the focus plane containing the smallest blur - with lower Strehl - on axis (dashed asigmatic plot),
off axis correction improves (shown boxed). Axial shift between the two planes is 1/45 mm. Astigmatism is
reduced to less than half with respect to the scope alone, in the process changing its sign, i.e. with the
tangential surface switching from left to right side on the astigmatic plot. Making the rear
element a bit more strongly curved would probably make the best axial and field-edge focus nearly coincide, but
difference would be near-negligible for imaging purposes. Entirely eliminating astigmatism would require
near-zero Petzval curvature, which might be possible with a 3-lens corrector, but the gain would be relatively
small, at least for this field size. Diffraction images show still compact central maxima at 1° off,
with well controlled lateral color
(for comparison, perfect Airy pattern for this system is in the top left corner).
55 - LOMO 102mm f/6.5 Triplet SuperApoFor some time out of production, this LOMO (Leningrad Optical Mechanical Association) triplet shared good reputation earned by this manufacturer. No prescrition was published, but a technical drawing of this lens can be found online. With the radii and spacings based on it, and assuming the most likely glass combination, it clicked in almost perfectly, with only slight adjustment needed to cancel the tiny coma residual. The front inner radii are equal, and the rear nearly so; it may be possible to make the latter equal as well, but it wouldn't affect correction.
This robust lens uses LZOS ED glass, OK4, and its BK7 equivalent, K8. It easily passes the "true apo" criterions, with its limiting polychromatic Strehl (photopic, 430-670nm) at 0.974 (best possible poly-Strehl is 0.98, with R1=299.5, and R4=-206.75). Over best image surface (-230mm radius), quality field is limited by astigmatism. At 1° off, 0.21mm of longitudinal astigmatism indicates 1.1 wave P-V wavefront error (0.21/(8*6.52)), which is level at which its diffraction image has cross-like form. It is about 0.02mm in size (varies with the star brightness), or 6-7 arc seconds suspended on the sky. In a 6mm 100° AFOV eyepiece at 110x magnification, it would be near the very edge of field, with angular size of ~12 arc minutes, thus clearly recognizable by the eye. It would become near point-like at about half the field radius (neglecting possible effects of field curvature of either objective, or eyepiece, or combined).
Being all but certain that this objective uses the K8/OK4/K8 glass comnination makes it more likely that
it is also the case with the APM/LZOS 130mm f/6 SuperApo (#23).
56 - The venerable short-tube 114mm f/8.8 "Jones-Bird" telescopeThis Newtonian configuration uses fast spherical primary with a simple lens corrector on the bottom of the focuser, correcting for spherical aberration and doubling, or so, the focal length. While some established companies also gave a shot to this configuration, it is mostly known as a low-quality product from annonimous sources. That earned to it "best to avoid" reputation. No official prescription is to be found, but as a low-cost telescope it is all but certain that it uses a simple doublet made of cheap glasses (there doesn't seem to be significant difference between air-spaced and cemented doublet). Such system is illustrated below, using an f/4 primary. Correction level changes somewhat with the focus height, so the two arrangements shown approximately outline the range between the near-maximum (#1) and near-minimum (#2) focus height.
Between the two, correction level for the central line gravitates to that of the mirror alone, if it was a paraboloid (box at right; the actual Airy disc of mirror alone is more than twice smaller, but it is made of even size for easier comparison). Center field correction can be practically perfect, with quality field limited by coma, and fairly strong field curvature (the latter is inconsequential in the presence of strong coma). Field curvature is more than twice stronger in the #1 arrangement. Off axis, it is somewhat better with the higher image plane, and somewhat worse with the lower. Chromatic correction is good, comfortably meeting the "true apo" criteria, except for the violet g-line, which is at the level of a 100mm f/50 achromat (as an average between the two arrangements). Unlike monochromatic correction, chromatism is lower with the lower focal plane, and higher with the higher. This telescope usually comes with simple, narrow-field eyepieces, which somewhat ameliorate bad effect of the strong field coma. It is certinly more portable than all reflecting f/8.8 Newtonian, but it has field correction comparable to an f/4 (with significantly stronger field curvature, which is, as mentioned, mainly irrelevant). And, it is not a Jones-Bird system (which corrects for coma too, and does not work well with the lens corrector so close to the focal plane). If placed in front of the diagonal, this simple "Barlow" corrector would reduce coma somewhat more, down to about 2/3 of coma with #1 arrangement. For the complete picture, the eyepiece has to be included. As already, mentioned, the run-of-the-mill variety of this telescope comes with simplest eyepiece types, usually Huygenians. Below is shown performance level with 10mm and 20mm units, for 100x and 50x magnification, respectively. Imaging element is OSLO "perfect lens", with 17mm focal length, which means that image scale corresponds to that of human eye. At 50x (20mm f.l. eyepiece), dominant off-axis aberration is coma, which is over 5 waves P-V at 0.3° (i.e. 15° distorsionless AFOV). That makes "diffraction-limited" (0.80 Strehl, or larger) field radius 1/40 degrees (0.44mm, or less than 0.4° AFOV). Required field edge accommodation is 0.66mm which, with one diopter of accommodation equaling 202/1000=0.4mm, little over 1.5 diopter on a convex toward the eye field. Since that implies that the edge point light pencil enters the eye slightly converging, the accommodation required is unnatural, requiring eye lens to relax beyond infinity - not as easy for the eye as natural accommodation by contraction, where it would correspond to accommodation from infinity to 0.6m object distance. At the field edge, tangential coma is about 0.07mm which, considering that 1mm on the retina corresponds to ~3.5 degrees, translates to about 1/4 degree, or 15 arc minutes. That makes it obvious to the eye, which on the average starts recognizing shape at about 5 arc minutes object size. In that respect, quality field - over which stars appear point-like - is about 1/4 of the full field.
At 100x magnification (10mm f.l. eyepiece), edge coma is 2.3 waves P-V, but its linear size is nearly as
large as at 50x. This is because the focal ratio is, due to the smaller exit pupil, twice larger, and so is the
image scale onthe retina. The aberration magnitude is smaller, but there is not much gain from it - at least not
in the outer field - as the diffraction images show. Required field-edge accommodation is 0.95mm, or 9.5 diopters,
well beyond the range for most people. 57 - Takahashi TOA 130mm f/7.7 triplet Ortho-ApoSome time ago I desided not to include it on this page, since it is already shown on the page with apo examples, but it does deserve more detailed presentation. No official prescription is given, not even an illustration of the objective, but the actual objective configuration hints at widely separated front element, and a near-contact rear pair. It is a PNP (positive-negative-positive) triplet configuration, which means it uses two ED-glass elements, specified by some vendors (but not Takahashi) as Ohara FPL53. Assuming it is FPL-53, the most likely glass for the middle element is BSL7, Ohara's equivalent of Schott BK7. There is a little wiggle room left after these assumptions are made, and the output matches the extraordinary correction level assigned to this objective.
Sherochromatism is practically cancelled, with the only remaining error being due to the residual - miniscule -
secondary spectrum. With 0.995 polychromatic Strehl (430-670nm, photopic) in its design limit, it offers
correction potential a cut above "super-apos". Note that here is given slightly faster, at f/7.5, so that it
can be directly compared to the "Chinese TOA". Interestingly, there is no appreciable difference
correction-wise between the two, even if one uses ordinary ED, and the other SD glass. 58 - Early Astro-Physics apochromatsEra of apochromatic telescopes in the US starts with Astro-Physics (AP) and Roland Christen. At that time, back in the 1980s, no today's extra-dispersion (ED) glasses where available, but were glasses with abnormal dispersion which was possible to use for a significant reduction in secondary spectrum, particularly with triplet objectives. Following information given in an article by Thomas Back (A Brief History of Astro-Physics Lenses, May 5. 1999.), several of these early glass combinations were raytraced, to find out how their level of correction - paricularly chromatic - compares to today's apochromats. All those objectives can be made coma-free, with similar, generaly low levels of off axis astigmatism and field curvature, so the results concentrate on axial correction. First models with specified glasses are from the period between 1981. and 1984. and relate to the "Super Planetary" series. They used either BK7/KzFS1(NASA)/BaF-10 or BaK1/KzFS1/BaFN10 combination (all Schott glass, except the NASA short flint KzFS1, a unique one-time production by Kodak/Baush&Lombard). There is no specific data on the NASA KzFS1 (it was made for NASA, hence the name); Roland Christen stated that it had better dispersion characteristics than the Schott version. The latter has significantly better performance, than a group of short-flint glasses that all share identical 613443 code (first three digits for the first three decimals after 1 in the index of refraction, and last three for the first three digits of their Abbe number). Despite sharing identical code, the difference in the blue/red and violet correction can be quite significant; for instance, the Ohara S-NMB51 would, in a 5" f/12 triplet have ~0.7 waves P-V in F and C, and over 3 waves in the violet g-line, while the closest to the Schott KzFS1, Corning FBC13-44, only comes to ~0.3 waves P-V in the blue and red, and ~2 waves in the violet (compared to less than 0.2 wave P-V in F/C and ~1.45 wave in the violet, as shown below).
The BaK1/KzFS1/BaFN10 is unusual in that has better correction in the violet than deep red. Both combinations are comfortably above the 0.95 polychromatic Strehl (430-670nm, photopic) at f/12, although falling a little short in the "true apo" requirement that deep red and violet need to be less than 1/2 wave P-V (both lines have very low sensitivity in the photopic mode, and have little influence on the polychromatic Strehl; they, however, become more significant in typical field conditions, when eye sensitivity shifts toward mesopic mode). Note that the KzFS1 is the Schott variety hence the triplet using BK7 - the actual AP objective - has a better correction than shown. At f/6, correction level expectedly drops, but not far from "diffraction limited" in its design limit. Later versions of the Super Planetary used as the abnormal glass Schott KzFS4, either with BaK1 or K7 for the front element. Correction level is nearly identical with either, with a small difference coming from a slight change in the positive-to-negative power balance. While the error in violet is far too large to satisfy the P-V requirement for a "true apo", the polychromatic Strehl at 0.96 is more than high enough for it.
All these objectives are similar in that they are close to the minimum of spherical aberration with all four inner radii equal. Here, optimizing for spherical aberration is done by making a small change in one of them. It can be also done by refiguring the middle element, which results in two pairs of equal radii. Such objective can be either left air-spaced, or filled with oil - or cemented, for that matter - without appreciable change in its color correction. By 1990, the modern ED glasses became available, and Astro-Physics switched the gear up: its EDT series now uses FPL52 and (little later) FPL53 glass, making possible faster, and still better corrected triplets. These mark the beginning of apochromatic refractors as we know them today. Exampless below illustrate the improvement in color correction made possible with the new generation of abnormal glasses.
What earned to the Astro-Physics' apochromats exceptional reputation, in addition to the use of glasses producing
high level of chromatic correction, is as much its great attention to lens smoothness and central line correction,
necessary for a high overall optical quality. Coupled with uncompromising finish quality, it spelled a recipe for
high-quality refractors by other refractor makers that followed. 59 - Sky-Watcher K100 100mm f/10 Klevtsov-CassegrainAvailable overseas, this small version of Klevtsov-Cassegrain comes with the Mini Virtuoso GTi mount. While no prescription is published, system drawing that can be found on vendor sites supplies information needed to closely reconstruct it optically. With ~f/2/4 primary, ~6mm thick meniscus, and given primary-to-meniscus and meniscus to secondary separation, the rest of parameters is closely determined by the requirement of having an optimally corrected f/10 final system. Central obstruction of the system below is fairly large at 42%, linearly, and the actual system could have it a bit larger.
At its design limit, central line Strehl is 0.97, and polychromatic Strehl (photopic, 430-670nm) is only slightly lower at 0.969, implying practically zero axial color error. The 0.46mm longitudinal astigmatism at 0.5° off axis implies 1 wave P-V wavefront error, resulting in a cross-like diffraction image. Best image curvature seems exeptionally strong at -64mm radius, with the corresponding 0.5mm longitudinal displacement from axial focus for this zonal height converting to 5 diopters accommodation requirement with 10mm f.l. eyepiece (infinity to 0.2m). Since a standard 10mm f.l. eyepiece has about that large linear field, it would be barely passable for most people, and wider-field units would require even more accommodation. Partial accommodation would result in a more or less vertically elongated star image. With 20mm f.l. standard eyepiece, field displacement is four times larger, with the accommodation requirement also 5 diopters (with diopter of accommodation closely approximated by f2/1000). This, of course, neglects astigmatism and field curvature of the eyepiece itself, which can significantly change the final best image field curvature.
System baffle tube extends to the final focus, which means that the limit to the image field is set by
the inner baffle tube diameter. Illustration shows the rear baffle tube (RBT) opening to be ~27mm in diameter,
with the front baffle tube (FBT) opening somewhat wider, ~31mm. The latter allows for nearly fully illuminated
field, but could compromise baffling efficiency. In all, if well made it can have high correction level, but
field edge performance may be compromised (varies individually),
due to the very strong best image curvature. 60 - Astro-Physics 155mm f/7 StarFire EDFIntroduced back in 1993. this oil-spaced triplet (aspherised) uses FPL53 sandwiched between two unspecified crown glasses. It's been marketed as a telescope optimized for astrophotography, featuring 4-inch focuser and field flattener. Its prescription hasn't been published, but Company Seven did publish its LA graph, which can be used to extrapolate its color correction parameters. The original graph has somewhat rough, broken plots, so for the purpose of evaluating it a smoothly curved plots - as they are supposed to be - interpolated to the original ones are used (below). Due to aspherization, higher order spherical aberration is absent, and the longitudinal aberration (LA) for 4th order spherical are related to the corresponding best focus P-V wavefront error as P-V=LA/64F2. The error is four times larger at either paraxial, or marginal focus location, with the relative error magnitude (1 at the best focus) for any point in between given as w = [16 + 15Λ(Λ-2)]1/2, with Λ being the relative placement of the focus location within the longitudinal aberration normalized to 2 (i.e. Λ=0 for focus point coinciding with paraxial focus, Λ=1 for point midway between paraxial and marginal focus, and Λ=2 for point conciding with marginal focus). It is all that's needed for obtaining the coresponding best focus P-V wavefront error, which is for primary spherical 3.354 times larger than the RMS wavefront error, with the latter determining the Strehl ratio value. Error at the location of e-line focus is then obtained by using Λ value corresponding to that point for each wavelength. Error in the e-line is too small to be measured with sufficient accuracy (it is also low enough to be affected by the very low higher-order aberration residual), but its Strehl value is known, being specified as 0.99.
Extracted values for best focus location - which for primary spherical corresonds to 0.707 zone - are very low. Even the violet h-line is close to the "diffraction-limited" level, and infrared t-line is below 1/2 wave. However, since their best foci are more or less separated from the e-line best focus - which is evidently the optimized line - their errors at that focus location are larger. Still, the lens comfortably passes the technical "true apo" criterion, requiring less than 1/4 wave P-V wavefront error in F (486nm) and C (656nm), and less than 1/2 wave in g (436nm) and r (706nm) line. Considering that far red and violet have very little influence on the photopic Strehl, and F and C still relatively small, it is likely that the photopic Strehl is above 0.95, also satisfying the "true apo" requirement.
But this is for the correction mode optimized for CCD/photography.
With a slightly weaker positive power, all wavelengths except those beyond g-line would have best foci shift closer
to the e-line focus, resulting in significantly smaller errors. In other words, the overall correction is
compromised just in order to keep violet light beyond g-line - which matters little to none for visual observations -
from disintegrating beyond certain level (perhaps determined by having the h-line plot completely contained within
the +/-0.3mm LA range). Even so, as already mentioned, the lens easily satisfies the
"true apo" criterion. 61 - 190mm f/16 Popp-MaksutovRecently, question was raised on astro forum whether an older Maksutov-Cassegrain telescope, made by Eugen Popp (Switzerland) probably in the late 1970s, can be regular Gregory-Maksutov (i.e. with aluminized spot on the rear site of meniscus corrector as secondary mirror), considering its unusually short tube. It is specified as 190mm aperture and 3200mm focal length (f/16.8), which somewhat differs from the official offering by the company from that time, consisting from 110,150,200,300, 450 and 600mm apertures, all f/16, and all with f/2.5 primary. Taking it is a 190mm f/16 system - which makes it very similar to the 200mm f/16 system, here's what raytrace shows. With canonical D/10 meniscus thickness, an all-spherical system nearly fits in the given configuration, with the tube length about twice its width. Central obstruction is 0.24D, also nearly corresponding to the size of the aluminized spot.
As expected with an f/2 primary, the longitudinal aberration (LA) graph shows significant higher-order spherical aberration residual which, even when optimally balanced with the lower order, limits center-field correction to 0.064 wave RMS, or 0.81 Strehl (with most aberrations, this RMS wavefront error value would result in ~0.85 Strehl, but the balanced secondary spherical, due to its extra wrinkle on the wavefront and high zonal slopes, has more detrimental effect on phase combining). Off axis, quality field is primarily limited by coma, although spherical aberration and astigmatism farther off are not quite negligible. Diffraction limited field (0.80 Strehl) is quite small, about 3.4mm (less than 4 arc minutes) in diameter, due to the large center-field error. At 21mm off axis, point displacement due to the field curvature is little over 1mm (away from the eye), which would require less than 1/2 diopter of accommodation with a standard 50mm eyepiece. Hence, even if appearing significantly curved, the visual field is essentially flat (even if using 30mm eyepiece with 83° field, required accommodation would be little over 1 diopter). Chromatism is practically non-existent, with the center-field polychromatic Strehl (photopic) at 0.81. Configuration can't be changed, because the rear meniscus radius value is determined by the need to minimize spherical aberration and longitudinal chromatism. Change in meniscus thicknes would result in small changes of back focal length and meniscus-to-primary separation. With a 15mm thick meniscus, for example, meniscus radii are somewhat stronger, and for f/16 focal ratio meniscus-to-primary separation is about 2mm smaller, and back focal length about 20mm shorter. The center-field RMS wavefront error is stil below 0.07 wave, but the corresponding Strehl falls below 0.8.
Apherizing the primary to -0.2 would take coma away, and increase center-field Strehl to 0.92+, but due to the
more relaxed meniscus radii an f/16 system
would require both larger central obstruction and significantly more of back focal length (290mm), which
rules out this option. On the other hand, just putting 6th order term on the primary would make possible to
practically eliminate spherical aberration, with back focal length about 10mm shorter than in the all-spherical
arrangement. It would make off-axis coma stronger, putting diffraction-limited field radius at 3.7mm
(comparable to f/6.9 paraboloid). However, considering generally low price of these telescopes, and their less
than stellar performance level, such configuration is unlikely. It would be certainly desirable for larger
Popp-Maksutov units, since the center field error scales with the aperture. Another option is to make the
primary slower. It could be what has been done, since some Popp-Maksutovs appear to have longer tubes than
this unit.
◄ 14.3. Observatory telescopes
|


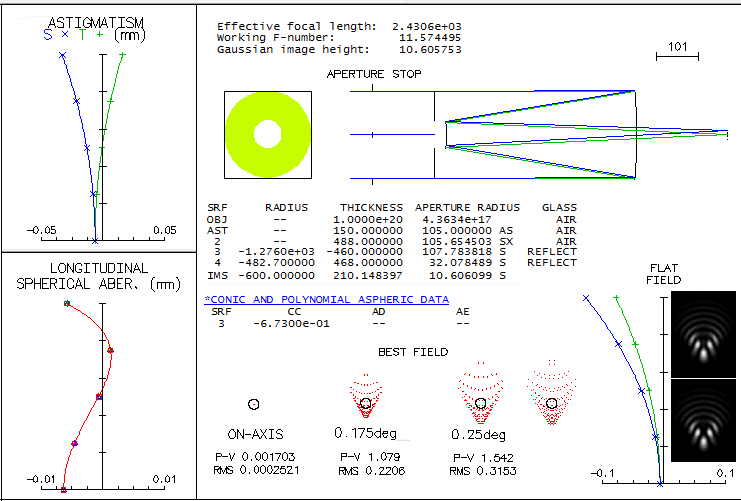
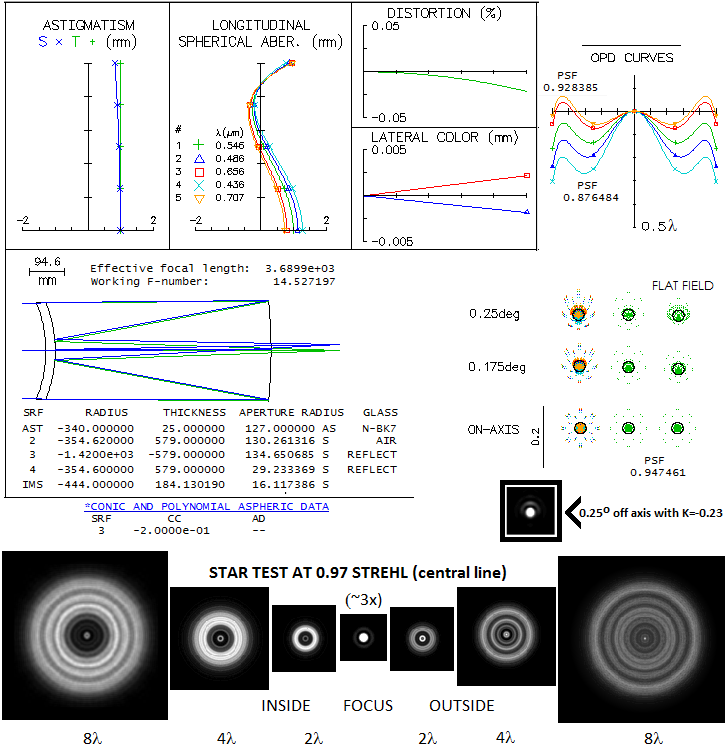
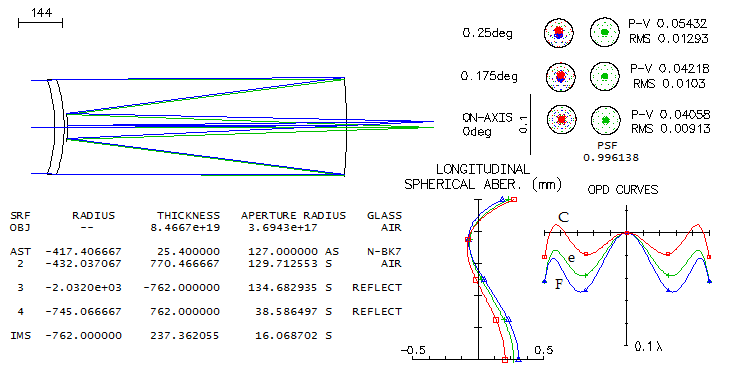

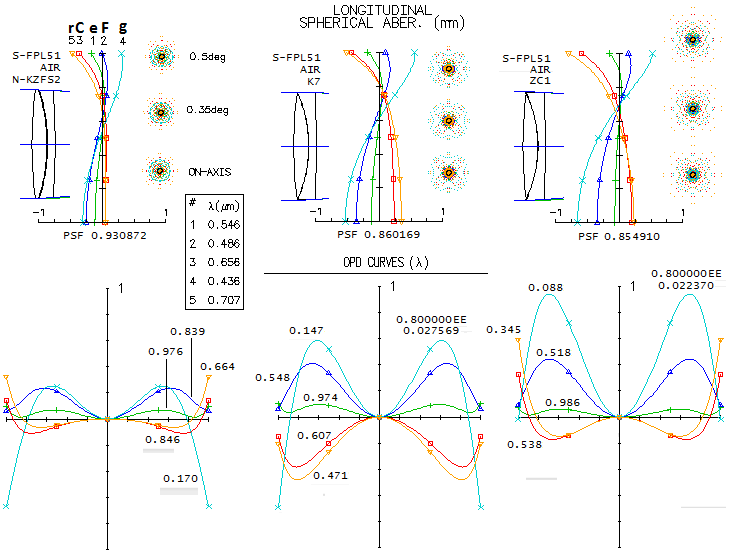 Performance level is near-identical with either ED glass. Chromatic and
overall correction is better when combined with K7 than K10 (not shown),
despite the latter allowing for significantly more relaxed inner radii.
Best correction level - near the "true apo" minimum - is with N-KZFS2, but it is
unclear why it is not better known as a lens objective glass choice.
Note that the Chinese (CDGM) equivalent to the Schott K7, H-K6, is
quoted as being 4.5 times more expensive than their BK7 equivalent
(H-K9L), with Schott K7 being only 2.10 times the N-BK7 price. Another
possible Chinese match, H-K10 (equivalent to the Schott K3, now obsolete),
quoted at 3.2 times the H-K9L price, produces similar output,
somewhat tighter in the red and blue, but with larger error in the
green and violet. There is no Chinese equivalent for the Schott N-KZFS2
short flint.
Performance level is near-identical with either ED glass. Chromatic and
overall correction is better when combined with K7 than K10 (not shown),
despite the latter allowing for significantly more relaxed inner radii.
Best correction level - near the "true apo" minimum - is with N-KZFS2, but it is
unclear why it is not better known as a lens objective glass choice.
Note that the Chinese (CDGM) equivalent to the Schott K7, H-K6, is
quoted as being 4.5 times more expensive than their BK7 equivalent
(H-K9L), with Schott K7 being only 2.10 times the N-BK7 price. Another
possible Chinese match, H-K10 (equivalent to the Schott K3, now obsolete),
quoted at 3.2 times the H-K9L price, produces similar output,
somewhat tighter in the red and blue, but with larger error in the
green and violet. There is no Chinese equivalent for the Schott N-KZFS2
short flint.
 It has practically perfect achromatism, but spherical aberration sets the
correction limit to a nearly 0.92 Strehl in the all-spherical version, and ~0.96 in
the one with aspherized primary (aspherization is determined by eliminating coma;
further aspherization would make spherical aberration still lower, but would start
inducing coma of opposite sign - for instance, putting -0.3 conic on the primary
would produce a system with 25% less coma than with spherical primary, and the
limiting axial design Strehl of 0.99). Astigmatism is negligible, but it is present:
the 0.34mm longitudinal error at the field edge implies 0.37 wave P-V, or 0.80 Strehl
level.
It has practically perfect achromatism, but spherical aberration sets the
correction limit to a nearly 0.92 Strehl in the all-spherical version, and ~0.96 in
the one with aspherized primary (aspherization is determined by eliminating coma;
further aspherization would make spherical aberration still lower, but would start
inducing coma of opposite sign - for instance, putting -0.3 conic on the primary
would produce a system with 25% less coma than with spherical primary, and the
limiting axial design Strehl of 0.99). Astigmatism is negligible, but it is present:
the 0.34mm longitudinal error at the field edge implies 0.37 wave P-V, or 0.80 Strehl
level.
 Arrangements A and C are very similar in their design limit, while B
has more spherochromatism, as indicated with its deeper aspherics. The starting all-spherical
system has about 1 wave P-V of secondary spherical, about 0.2 wave of tertiary spherical (of
the same sign), and little over 1/90 wave of 10th order spherical. The reason why A and C
have less spherochromatism is that reducing 4th order spherical to near zero by
manipulating corrector radii makes them more relaxed, hence all higher-order terms are
smaller. How deep are these higher order curves, that need to be carved into the
existing surface radius? Since OSLO calculates values for the correction at the
paraxial focus, each higher-order term grows from zero on axis to the maximum
at the edge, with the exponent equaling the order. So the secondary (6th order)
spherical aberration term of 1.8e-13, needed to reduce it to near zero, gives
the depth of glass to be taken of the edge when multiplied with the surface
semi-diameter raised to 6th power - in this case 0.0014mm (this is about 2.5 times
larger than the error at the best focus location, which is about 1 wave P-V; if correction
was made at this focus, the needed curve depth would be 2.5 times smaller, maxing out at the
0.76 zone and falling back to zero at the edge). Since all terms are of the
same sign, they add up (note that the 4th order aberration term is
only a small correction of about 1/14 wave P-V that was little easier for me to put here, than
to fiddle with corrector radius).
Arrangements A and C are very similar in their design limit, while B
has more spherochromatism, as indicated with its deeper aspherics. The starting all-spherical
system has about 1 wave P-V of secondary spherical, about 0.2 wave of tertiary spherical (of
the same sign), and little over 1/90 wave of 10th order spherical. The reason why A and C
have less spherochromatism is that reducing 4th order spherical to near zero by
manipulating corrector radii makes them more relaxed, hence all higher-order terms are
smaller. How deep are these higher order curves, that need to be carved into the
existing surface radius? Since OSLO calculates values for the correction at the
paraxial focus, each higher-order term grows from zero on axis to the maximum
at the edge, with the exponent equaling the order. So the secondary (6th order)
spherical aberration term of 1.8e-13, needed to reduce it to near zero, gives
the depth of glass to be taken of the edge when multiplied with the surface
semi-diameter raised to 6th power - in this case 0.0014mm (this is about 2.5 times
larger than the error at the best focus location, which is about 1 wave P-V; if correction
was made at this focus, the needed curve depth would be 2.5 times smaller, maxing out at the
0.76 zone and falling back to zero at the edge). Since all terms are of the
same sign, they add up (note that the 4th order aberration term is
only a small correction of about 1/14 wave P-V that was little easier for me to put here, than
to fiddle with corrector radius).
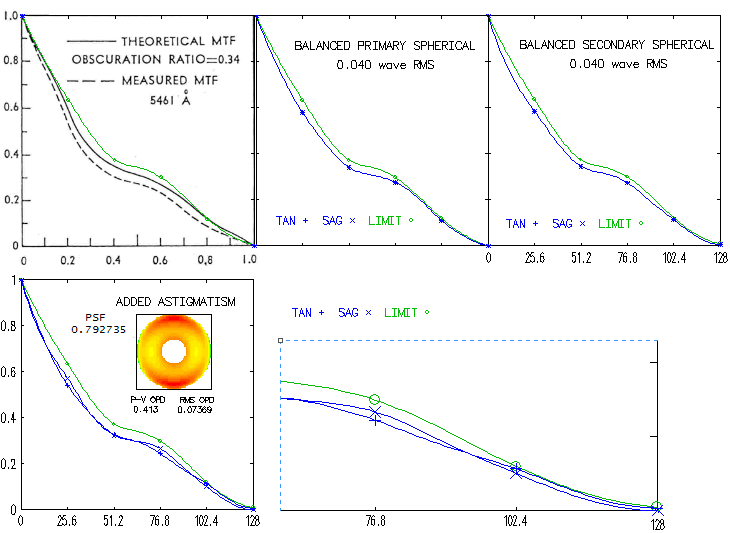 Worse yet, its limiting contrast for the 0.34 relative obstruction size is not acurate, and the
measured "typical" MTF has an odd
form, with the most of contrast loss toward high frequency range (top left, with the green
line representing the proper MTF for 0.34 relative central obstruction). No known aberration
produces such an MTF. It would require enlargement of the central maxima, without
spreading energy beyond it. The closest that comes to it is astigmatism, and only
in one orientation. Adding astigmatism to the all-spherical arrangement,
to make the two MTFs roughly similar (bottom left, more contrast loss in the lower frequencies range,
less in the high frequency range), results in the overall error at the
level of 0.80 Strehl. In other words, the Questar's own graph implies this level of
correction: 0.80, or so, Strehl wavefront on top of 0.34 relative central obstruction.
The question is, if the telescope has "
Worse yet, its limiting contrast for the 0.34 relative obstruction size is not acurate, and the
measured "typical" MTF has an odd
form, with the most of contrast loss toward high frequency range (top left, with the green
line representing the proper MTF for 0.34 relative central obstruction). No known aberration
produces such an MTF. It would require enlargement of the central maxima, without
spreading energy beyond it. The closest that comes to it is astigmatism, and only
in one orientation. Adding astigmatism to the all-spherical arrangement,
to make the two MTFs roughly similar (bottom left, more contrast loss in the lower frequencies range,
less in the high frequency range), results in the overall error at the
level of 0.80 Strehl. In other words, the Questar's own graph implies this level of
correction: 0.80, or so, Strehl wavefront on top of 0.34 relative central obstruction.
The question is, if the telescope has "