|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
9.2. Refracting telescope objectives: Apo
and semi-apo
▐
9.3. Designing doublet achromat
►
9.2.1. Semi-apo and apo lens objective examples
Within constraints given on previous page, a number of apochromatic and some viable
semi-apochromatic glass combinations are possible. More than a few have
been, at some point in time, used for commercial refracting telescopes.
Following table lists examples of such objectives, from those with
small reduction in secondary spectrum, to those fulfilling the formal apochromatic condition. All achromats in comparison are assumed with near-equal
wavefront error in F and C (Δf is the
secondary spectrum in units of that in a comparable achromat, and SP
is the polychromatic Strehl for the 440-670nm spectral range, photopic
sensitivity; WFE=wavefront error). Somewhat arbitrarily, objective's
mode of correction is classified based on its secondary spectrum vs.
that in the standard achromat as enhanced achromat (EA) if less than
two-fold reduced, semi-apochromat (SA) if two-fold to nine-fold reduced,
and apochromat (A) if reduced by tenfold or more. According to their polychromatic Strehl, objectives range
from sensibly perfect (SP>0.95)
to fair (0.7<SP<0.8)
depending on two variables: their mode of correction, and their relative
aperture (glass dispersion: ● "normal" i.e.
common, ● partly
abnormal, ●
"abnormal" i.e. very low dispersion).
| # |
D
(mm) |
f |
GLASS
RADII / THICKNESS // SEPARATION
(mm) |
Δf1 |
RMS WFE
(RATIO v. ACHR) |
SP
(ACHR) |
| Element 1 |
Element 2 |
Element 3 |
e |
(F+C)/2 |
g |
r |
| 1 |
100 |
12 |
BAK1
789, -267/11//0.6 |
BASF52
-277, -1430/6 |
- |
.79
EA |
.007 |
.22
(.76) |
1.2
(.85) |
.36
(.82) |
.86
(.81) |
| 2 |
150 |
10 |
BK7
910, -330/16//1 |
KZFSN4
-339.5, -1818/9 |
- |
.75
EA |
.017 |
.37
(.71) |
2
(.78) |
.69
(.74) |
.75
(.71) |
| 3 |
100 |
15 |
BK7
880, -187.3/11//0.15 |
KZFN2
-188, -3900/7 |
- |
.73
EA |
.003 |
.18
(.78) |
.88
(.78) |
.32
(.77) |
.89
(.84) |
| 4 |
150 |
15 |
BALF5
1494, -372/17//0.7 |
BASF52
-391, -1800/9 |
- |
.72
EA |
.017 |
.25
(.73) |
1.35
(.80) |
.40
(.64) |
.83
(.77) |
| 5 |
150 |
12 |
BAK1
1000, -310.4/17//2.1 |
KZFSN4
-31, -6630/9 |
- |
.47
EA |
.017 |
.20
(.46) |
1.26
(.59) |
.28
(.36) |
.86
(.73) |
| 62 |
150 |
6.5 |
BAK1
484, -1440/12 |
KZFSN4
-1440, 203.8/8 |
BAK1
203.8, -7300/16 |
.47
EA |
.020 |
.37
(.37) |
2.3
(.45) |
.54
(.39) |
.76
(.61) |
| 72 |
150 |
10 |
BK7
1862, -365.4/14 |
KZFS1
-365.4, 365.4/6 |
BAFN10
365, -1343/14 |
.15
SA |
.018 |
.07
(.13) |
.56
(.22) |
.084
(.09) |
.94
(.71) |
| 82 |
150 |
8 |
BAK1
1711, -235/16 |
KZFSN4
-235, 277/9 |
BAFN10
277, -1430/14 |
.13
SA |
.018 |
.10
(.24) |
.85
(.40) |
.10
(.13) |
.87
(.67) |
| 9 |
150 |
15 |
BALF4
603, -244.25/18///0.09 |
KZFN2
-243.75, 166.6/6.2//6.4 |
K7
172.4, 927.7/16 |
.1
A |
.015 |
.039
(.11) |
.52
(.31) |
.021
(.034) |
.954
(.77) |
| 10 |
127 |
9 |
KF3
551, 192/8//0.15 |
FK01
192.2, -13600/12 |
- |
.22
SA |
.006 |
.10
(.21) |
.62
(.26) |
.18
(.20) |
.93
(.72) |
| 113 |
100 |
7 |
FK51
390, -127/15//0.6 |
ZKN7
-127, -1464/7 |
- |
.01
A |
.046 |
.10
(.20) |
.24
(.10) |
.13
(.15) |
.83
(.71) |
ZKN7
348, 100.5/6//0.6 |
FK51
100.5, -2727/15.5 |
|
.059 |
.10
(.20) |
.23
(.10) |
.11
(.13) |
.78
(.71) |
| 123 |
100 |
7 |
FPL53
384, -156/14//0.37 |
ZKN7
-159, -750/6 |
- |
.01
A |
.024 |
.063
(.13) |
.15
(.06) |
.067
(.08) |
.93
(.71) |
ZKN7
278, 117.1/6.//0.46 |
FPL53
115.7, -3080/14 |
- |
.029 |
.066
(.13) |
.16
(.06) |
.062
(.07) |
.92
(.71) |
| 13 |
100 |
7 |
ZKN7
386, 204/7 |
FK51
204, -178/15 |
ZKN7
-170, -1500 |
.01
A |
.010 |
.050
(.10) |
.11
(.05) |
.077
(.09) |
.97
(.71) |
| 143 |
100 |
7 |
CaF2
379, -166/13//0.75 |
K5
-169.7, 699//6 |
- |
.07
A |
.022 |
.073
(.15) |
.15
(.06) |
.078
(.09) |
.93
(.71) |
K5
264, 121.2/6//0.22 |
CaF2
119.3, -3544/13 |
- |
.022 |
.074
(.15) |
.155
(.06) |
.081
(.09) |
.92
(.71) |
| 15 |
100 |
10 |
ZKN7
396, 165.3/6//0.4 |
FPL53
163, -4400/14 |
- |
.01
A |
.005 |
.025
(.07) |
.06
(.035) |
.020
(.033) |
.99
(.78) |
| 16 |
100 |
10 |
K5
378, 172/6//0.9 |
CaF2
169.3, -5060/13 |
- |
.07
A |
.004 |
.034
(.1) |
.07
(.04) |
.041
(.066) |
.984
(.78) |
| 172 |
140 |
7 |
K10
479, 277/12 |
FPL53
277, -359/21 |
BK7
-359, -1252/12 |
.124
A |
.011 |
.052
(.075) |
.33
(.1) |
.066
(.054) |
.955
(.64) |
| 182 |
140 |
7 |
ZKN7
420, 222/10 |
FPL53
222, -486/19 |
ZKN7
-486, -1880/10 |
.01
A |
.013 |
.040
(.058) |
.17
(.05) |
.068
(.056) |
.970
(.64) |
| 192 |
140 |
7 |
K7
448, 268/10 |
CaF2
268, -360/21 |
K7
-360, -1300/10 |
.03
A |
.012 |
.043
(.062) |
.16
(.047) |
.045
(.037) |
.965
(.64) |
| 20 |
130 |
7.7 |
FPL53
2380, -262.2/12///22.9 |
BSL7
-239.8, 2580/7//1 |
FPL53
444, -926/11 |
.025
A |
.003 |
.029
(.048) |
.029
(.017) |
.065
(.032) |
.987
(.64) |
| 21 |
140 |
7 |
ZKN7 580,
293/9//1
FPL53
293, 2500/13//920 |
920mm
interspace |
FPL53
537, -227.7/12//
1
ZKN7
-232.1, -1170/7 |
.01
A |
.003 |
.033
(.048) |
.06
(.017) |
.027
(.032) |
.983
(.64) |
1Measured as the
longitudinal separation between the common C/F focus and best
e-line focus, in units of that in a comparable standard achromat
(not a reliable indicator of chromatic correction in the
presence of significant spherochromatism)
2Triplets with two
pairs of conforming inner radii and zero lens separation can be
assumed to be oiled triplets; for simplicity, oil medium is
omitted, with zero lens separation (it generally has a minor effect)
3Top specs are for
the ED glass element (the positive one) in front, bottom for ED
glass in rear; in general, the latter requires more strongly
curved inner radii, with more spherochromatism
4Approximately; based
on the offsetting RDP differentials for K10 and BK7 vs. FPL53,
the former nearly four times greater, but the latter in a nearly
twice stronger lens, resulting in an effective RPD differential
of roughly twice that of BK7 |
TABLE 12:
Examples of lens objectives with enhanced chromatic correction vs.
standard doublet achromat, starting with combinations of normal and
partly abnormal glasses, toward objectives using abnormal (very low
dispersion) glasses:
#1, 2, 3, 4
- enhanced doublet achromats with one somewhat abnormal glass;
#5 - further enhanced
doublet achromat, with less than half the secondary spectrum of the
standard achromat (#3 is the Zeiss AS objective),
#6 - triplet achromat with the same glasses as
previous, having only slightly more of higher-order spherical in the optimized
wavelength (it would have made the doublet useless at this f-ratio);
#7 - triplet using one of
glass combinations in the early AstroPhysics triplets, approaching 0.95
Strehl at
f/10;
#8 - triplet with a similar
correction level at
f/8; note how much use of different
glass for the second, positive element, with an offsetting RPD
differential versus first element, further reduces secondary spectrum
#9 - an early triplet
form (Zeiss B type), modification of the Taylor's photo-visual triplet;
#10 - older Meade doublet
apo;
#11, 12 - two apo
doublets with similar reduction in secondary spectrum, but with
significant variation in the level of spherochromatism due to their
respective Abbe differentials,
#13 - same glasses as in #11, but in a triplet form, greatly
reduce spherochromatism; #14
- calcium fluorite doublet at the same focal ratio doublet as #11-13
(it is hard to find a better match for CaF2 at this fast focal ratio
even among lanthanoids - with the Chinese H-Lak52, similar to the
Schott N-Lak34 and Ohara S-Lal18, it reaches 0.95 polychromatic
Strehl, but that could be about as good as it gets);
#15 and #16 - doublets
with the same glasses as #12 and #14, respectively, become practically
perfect at
f/10;
#17 - triplet with glass
combination used in TEC's 140
f/7 apo;
#18, 19 - triplets with
identical aperture/f-ratio
and different glass combinations;
#20 - Takahashi TOA type
triplet #21 - same aperture/f-ratio
objective with identical glasses as #18 triplet in the Petzval
arrangement
Some of the above objectives do not have the optimum, even acceptable
relative aperture if the principal criteria is highest level of
chromatic correction. The purpose is to illustrate the limitations of
particular type of objectives. Numerical data is graphically illustrated
by the respective longitudinal aberration (LA) plots and ray spot plots (FIG.
149; note that the black circle is the Airy disc in the e-line,
which is of
constant size for any given objective; variation in its size is due to
the need to fit blurs of often very different sizes together).
Most of LA graphs for doublets and fast triplets show
mixture of 6th
and 4th order spherical aberration.

FIGURE 149: Secondary spectrum and spherochromatism in the objectives from
Table 12. While formally defined as the longitudinal separation between
the common red blue (F/C) focus and green (e-line), all paraxial (here,
on the horizontal scale; note that the size of scale varies), actual
location of these foci is shifted due to the presence of
spherochromatism. In general, the paraxial blue focus is shifted closer,
and the red focus about as much farther away from where that common
focus would have occurred. Obviously, if they would be
nearly coinciding, the wavefront error would have been significantly
greater in the shorter wavelength, more so due to it being overcorrected
(when reading these plots, it is important to keep in mind that all the
zones at the aperture radius - represented as the vertical scale - focus
at the horizontal scale; the foci are merely projected up to the zonal
height, forming the
longitudinal aberration plot).
The magnitude of F/C
paraxial separation for given level of spherical aberration is somewhat
arbitrary; it is often such that F and C-line ray spots are
nearly equal in size. Since in that case the wavefront error is greater
in the F - not the best mode considering that eye sensitivity is higher
in the blue line, even in the photopic mode, and more so toward mesopic
mode - refracting objective here are generally brought to a near equal
wavefront error in F and C.
Plots for objectives
#1-5 show F and C lines
clearly separated from the
e-line, indicating the presence of secondary spectrum (these five
objectives only show these three lines, since r and ,
particularly, g, are far enough to squeeze F, C and
e too close together on this image scale). Secondary spectrum is
significantly reduced in #6,
a fast triplet using somewhat abnormal short flint for its central
element (typically for short flint combinations, the violet end runs
away). It is still more reduced in
#7, a triplet combo of
the early NASA Christen triplet combo;
#8, also an Astrophysics'
triplet combo from the 1980s, uses another short flint, originally made
for NASA (reportedly, a bit better than Schott's KZFSN4 available today
only as a special melt); it does form a typical apo C/F/e crossing
at about 76% zone, but some residual secondary spectrum is still
evident, since F and C paraxial foci are at unequal
separation from paraxial e focus (by slightly strengthening the
negative power, F could be brought to coincide with C but,
since C is farther away from e than F, this common
focus would be be falling somewhat behind e). In
#9, an early Zeiss
triplet, secondary spectrum is nearly eliminated, but higher order
spherical creeps in due to the strong surface radii, even at
f/15. A more recent doublet, the older Meade
"apo" at #10, with
Hikari's FK01 ED glass (near-equivalent to Ohara FPL51), still has some
relatively significant secondary spectrum (at 127mm
f/9 its is still quite close to 0.95 visual
polychromatic Strehl). At #11,
very similar Schott FK51 ED glass, in combination with a common crown,
has secondary spectrum all but eliminated, but clearly shows
spherochromatism at
f/7 (both combinations, with the ED first,
and following the crown, are shown). Using ED with higher Abbe number
(i.e. lower dispersion), like FPL53 (#12),
or calcium fluoride (#14),
reduces spherochromatism, and even more does using the triplet form (#13).
Spherochromatism with these same glasses in a doublet form is, as
expected, significantly reduced at slower
f-ratios (#15,
16). Larger fast objectives require triplet form for good
chromatic correction: #17
shows plots for TEC 140mm f/7 triplet combination optimized for visual
mode (the actual instrument is said to have 0.92 polychromatic Strehl,
which implies that the violet is being pulled closer, at the expense of
the optimum F/C correction, to improve its photo/CCD performance). If
such triplet was made with ZKN7 for the 1st and 3rd element (at a small
increase in the glass cost), secondary spectrum is practically
eliminated, but the overall gain is relatively small, because it is
spherochromatism, i.e. spherical aberration in non-optimized wavelengths
that causes most of the chromatic error (#18).
For the same reason, replacing FPL53 with fluorite and ZKN7 with one of fluorite's matching crowns
(K7), produces nearly identical correction (#19).
With somewhat wider air gap between the front and second lens element,
it is possible to practically eliminate spherochromatism (#20,
Takahashi TOA type triplet). Using the same glasses as in #18 in a 2-doublet Petzval arrangement reduces spherochromatism by reducing
the lower-order residuals due to index
variations and eliminating higher-order spherical, but it is still
present (#21).
However, the
added bonus of the Petzval is the flattened image surface (which is
curved to about 35-40% of the focal length in doublets and triplets);
residual astigmatism left in for that purpose is still less than half
the astigmatism of the triplets.
Aspherizing for reduction of higher-order spherical
aberration
All above systems utilize only spherical surfaces.
While it is a plus with respect to ease of fabrication, it is also a
limitation with respect to correction of higher (6th) order spherical
aberration (secondary astigmatism is generally negligible, and secondary
coma low in comparison, easy to reduce to negligible by balancing it
with the primary coma). Aspherizing a surface does not appreciably
change the ray height on it, but it does change surface profile,
bringing it either closer or farther away (depending on the sign of the
aspheric) from the 6th order surface approximation (FIG.
37), as well as changing the incident angle.
When significant, higher-order spherical affects
not only the level of correction in the optimized wavelength, but also
adds to spherochromatism (since it changes surface profile, it also
affects longitudinal chromatism, and may require slight adjustment in the
radii power balance). Removing 6th order spherical by way of aspherizing
also tends to lessen the violet 4th order error, producing better color
balance. The effect is generally small, and may be marginally
significant in oiled objectives, due to the stronger aspherization
required to remove 6th order spherical aberration on an oiled surface.
The manner in which aspherization affects
spherochromatism is somewhat different in triplets vs.
doublets.
In doublets, the typical form of secondary spherical is undercorrection.
With it uncorrected, and with primary spherical corrected in the optimized
wavelength, a doublet is more undercorrected in the red (which is
undercorrected in primary spherical for zero primary spherical in
optimized wavelength, thus the two aberrations add up), while to some
extent balanced in the blue (which is overcorrected for zero primary
spherical in optimized wavelength, hence opposite in sign to that of
secondary spherical). When this residual secondary spherical is balanced
with primary spherical of opposite sign (overcorrected) by a slight
adjustment in one of the inner radii, it can be minimized only in one,
optimized wavelengths, while added primary overcorrection reduces error
in the red (tending to produce predominantly higher order spherical,
since added primary overcorrection partly offsets its primary undercorrection
component) and increases it in the blue/violet, by enlarging its primary
overcorrection component. Taking as an example the FPL53/ZKN7 doublet (#12),
those two stages are shown as first and second from left, respectively.
Since most of the lens' secondary spherical is generated by the slight
excess on the second vs. third surface, it can be eliminated by slightly
aspherizing either of the

two radii (prolate ellipsoid for the second, and oblate for the third
radius). To compensate for the induced primary spherical imbalance, one
of the other two surfaces, with the relatively low secondary-to-primary
aberration ratio, needs to be aspherized. The result is shown on the
third plot. Removing secondary spherical by aspherizing had no
appreciable effect on spherochromatism. The only significant change is
in the correction level in the optimized wavelength, but since it is
sufficiently low with all surfaces spherical, aspherization is not worth
the extra cost. Even if the 8TH order residual (about 0.05 wave RMS,
minimized to 0.012 wave by balancing it with the opposite in sign
primary spherical) is removed by putting a Schmidt-type aspheric on one
of the surfaces, the overall correction is not significantly better.
In the typical triplet, the residual secondary
spherical is most often overcorrected, while for cancelled primary
spherical in the optimized wavelength, the red and blue/violet are, like
with the doublet, undercorrected and overcorrected in the primary
spherical, respectively. Hence balancing this residual overcorrected secondary
spherical by adding primary spherical of opposite sign now lessens the error
in the red, producing a partially balanced 6th/4th order aberration, while increasing it in the blue/violet. Since the latter
typically already has significantly larger error, this creates more of a
red vs. blue/violet imbalance than in the doublet. Thus lessening this
imbalance through removing the lens' secondary spherical residual by aspherizing one or two surfaces will generally produce more of a
beneficial effect on overall correction than in a doublet. The
difference may and may not be significant.
It can be
illustrated on the ZKN7/FPL53/ZKN7 triplet (#18). While triplets with
equal pairs of inner radii are usually intended for oil-type lens, they
were given above as a cemented objective, without spacing and oil specs,
because small spacing of this type (usually a small fraction of a mm),
with or without oil, does not appreciably change lens' output (in this
particular case it only added about 1/20 wave P-V of primary spherical,
which can be corrected by a slight bending of the inner two radii pairs,
to 220/496mm). That's
because the aberrations at the inner four radii, which are dominant,
tend to change evenly, in proportion. However, the conics that works
with air-spaced triplet (which are nearly identical for the cemented as
well) will not work with the oil-spaced one. For instance, this
particular triplet if air-spaced will have its higher-order spherical
aberration excess nearly eliminated by putting -0.03 conic on the second
surface, and the primary spherical induced by that offset by putting
-0.225 conic on the front surface. And if lens' interspaces is filled
with oil, the needed conics are -0.5 and -.538 for the third and first
surface, respectively (third surface requires significantly less
aspherizing in this case). The output is also very different for the
air-spaced and oiled objective, as shown below (since OSLO Edu doesn't
list lens oils, prescription uses Schott KF6 crown which has similar
refractive index to some commonly used oils).

Compared to the non-aspherized air-spaced lens with all other specs
identical, removing higher-order spherical with aspherization did
somewhat reduce the error in the blue vs. red, but only by about 10%.
Thus removing 6th order spherical aberration residual with aspherization
wouldn't be justified with this particular lens, less so considering
that it would require double aspherization. The results are, however,
very different with the oiled lens. Due to the refraction being very
much suppressed by the higher refractive index in the interspace (1.52
for KF6 vs. 1 for air), the inner surfaces act as of significantly
weaker radii, requiring a higher nominal conic for canceling the 6th
order spherical imbalance. But the required change of surface profile to
remove 6th order spherical here also affects spherochromatism in the 4th
order spherical, simultaneously removing both, 6th and 4th order
spherochromatism. The result is a nearly zero-spherochromatism lens,
which is at
f/7 better corrected than TOA-type lens at
f/7.7 (note that a slight change in radii was
required to offset the effect of aspherization on longitudinal
spherochromatism; it increased the focal length about 1%).
Unfortunately, putting -0.5 conic on such a strongly curved surface (f/0.8
if mirror) - more so considering it is a hard to work with glass - is highly unappealing in terms of
related cost. The alternative of aspherizing non-FPL53 surfaces (0.4
conic on the first and -39 last surface) would eliminate the 6th order
residual, but with no reduction in spherochromatism.
However, the manner in which the 6th order excess is generated varies
with the glass combinations and lens configuration. The above example
is not a "good candidate" for aspherization, with double aspherization
required, and little to gain from it. The reason for double
aspherization here is that one surface needs to be aspherized in order to
minimize 6th order spherical, but this cannot be compensated for by
bending the mid element, due to the 6th order spherical aberration total
for the two inner surface pairs remaining significant. Thus
compensatory aspherization of another surface is necessary. This may
change with different glass combinations, different lens arrangement, or
both. For instance, this same glass combination but in the
positive-negative-positive (PNP) element arrangement - hence with the
matching glass sandwiched between two ED elements - only requires a single
aspherization, as shown below, can have its 6th order spherical
aberration residual eliminated by aspherizing a single non-FPL53
surface, with the primary
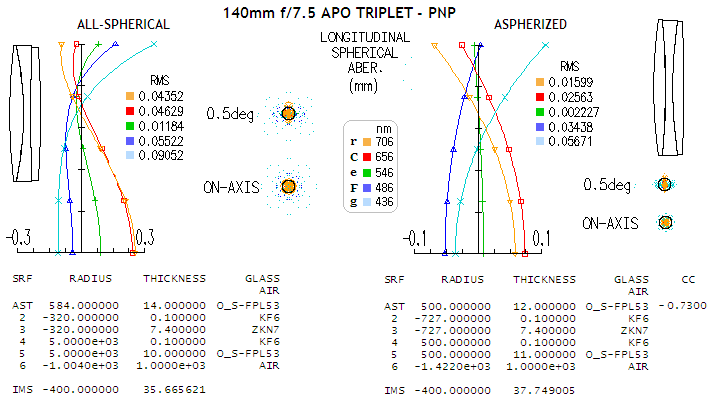
spherical induced by aspherizing neutralized by the aberration of
opposite sign induced by reshaping the mid element (first and last
radius are changed in order to minimize coma which was to a smaller
extent also induced by reshaping the mid element). As the LA graphs and
RMS numbers show, spherochromatism is significantly reduced with
aspherizing (note that F/C correction can be made still better, by
slightly weakening the positive vs. negative power, i.e. shifting red to
the left, and blue/violet to the right, at a price of g/r error
increase). The negatives are the relatively strong aspheric required,
and two ED glass element needed in the PNP triplet arrangement.
In order to be viable for aspherization, an NPN triplet has to use
different matching glasses. Here's an example where the matching crowns
are also Ohara, as well as the glass used to simulate the oil (nearly
identical to the Schott KF6 in the index and dispersion).

The aspherized LA plot is very similar to that of the published plot for
the AP 140mm
f/7.5 EDF triplet apo (in the published
lines, which are somewhat different, with the 460nm instead of 436nm, no
706nm and unspecified line in between e and F). There is
no way to know how close are these specs to the actual ones - except
that we know it is a NPN arrangement with FPL53 as the mid element - but
this fast and large triplet had to be aspherized in order not to show
the 6th order residual. While the spherochromatism is somewhat reduced
in the aspherized version, the gain is rather small. The red/blue-violet
imbalance is also slightly smaller with aspherizing (which should result
in a slightly whither white-star image), but even both combined make for
a rather small difference. It is important to note, though, that the
g-line LA is 25% smaller in the aspherized version, hence optimizing for
the violet would give the aspherized version a slight edge in this
respect. Still, the only rationale for aspherizing here would
be to bring the lens as close to perfection as possible (note that the
mid element in the AP lens is not equi-convex - the first surface is
more strongly curved, which may make it possible to aspherize only the
5th surface, perhaps less than in this example - but the point here is
to examine the gain from aspherizing, which should remain similar,
considering that the aspherized version's LA graph is nearly identical
to the published data for the AP lens).
However, this is only so in the context of the error magnitude expressed
as RMS wavefront error, or corresponding Strehl. Neither accounts for
the differences in the pattern of the disturbed energy and its possible
effects. Looking from the standpoint of distribution of the energy lost
from central maxima, the benefit from aspherization can be significant
even in this case (as well as in the case of the
doublet example). Even if
the RMS error decrease is relatively small, the effect on
ensquared energy
just from replacing balanced secondary spherical - and to a smaller
extend its partially balanced forms - with primary spherical at best
focus can result in appreciable benefit in imaging applications. It
could also be beneficial in visual use, since balanced 6th/4th order
(i.e. secondary) spherical aberration throws energy lost to the Airy
disc significantly farther away than primary spherical of similar
magnitude (FIG. 98). This generally
makes the wavelengths with the largest error - commonly the blue/violet
- more readily visible as a separate fringe coloration, particularly on
bright objects. While contrast-wise this shouldn't have significant
effect if the magnitude of aberrations remains similar, it could still
produce a noticeable cosmetic, i.e. color purity improvement in such
instances. It could also enhance imaging performance in these
wavelengths. Combined with the possible reduction in the 4th order
spherical due to aspherization, it could produce tangible overall
benefit in the performance level.
Spherochromatism and lens spacing
General rule for secondary spectrum is that it doesn't change appreciably
for any given combination of glasses, regardless of how many elements we
put together, or how we change the configuration. With spherochromatism,
however, things are different: change in configuration can cause change in
the level of different orders of spherical aberration. Certain configurations
can have these different orders have compensatory effect, significantly
reducing spherochromatism. It is more pronounced with the change of
lens spacing. An example are Takahashi TOA objectives, but since
they use unortodox configuration with two ED glass elements, the effect
will be illustrated on a stundard NPN triplet with a single ED glass.
Picture below shows a triplet modified to reduce spherochromatism (top)
vs. standard triplet form (middle). The former was posted on Cloudy Nights
forum, by user RayG, and uses very wide second spacing to constructively
change the proportions of spherical aberration orders (all graphs are with
the same scale, so they can be directly compared; the ray spot plots are
twice smaller for the mid and bottom objective). As a result, the LA graph
is significantly tighter than for the standard triplet, as well as the OPD (optical
path difference, i.e. wavefront error) curves. Reduction in spherochromatism
is reflected in the respective polychromatic Strehl values, 0.951 vs. 0.934 photopic and
0.849 vs. 0.788 average CCD. Chromatic focal shift graphs - which show how
paraxial foci of different wavelengths deviate from the paraxial focus of
optimized wavelength - are noticeably different, with the modified triplet
having, expectedly, smaller deviations, except in the infrared (chromatic
focal shift is not the primary indicator when spherochromatism dominates,
but becomes more meaningful as spherochromatism diminishes).
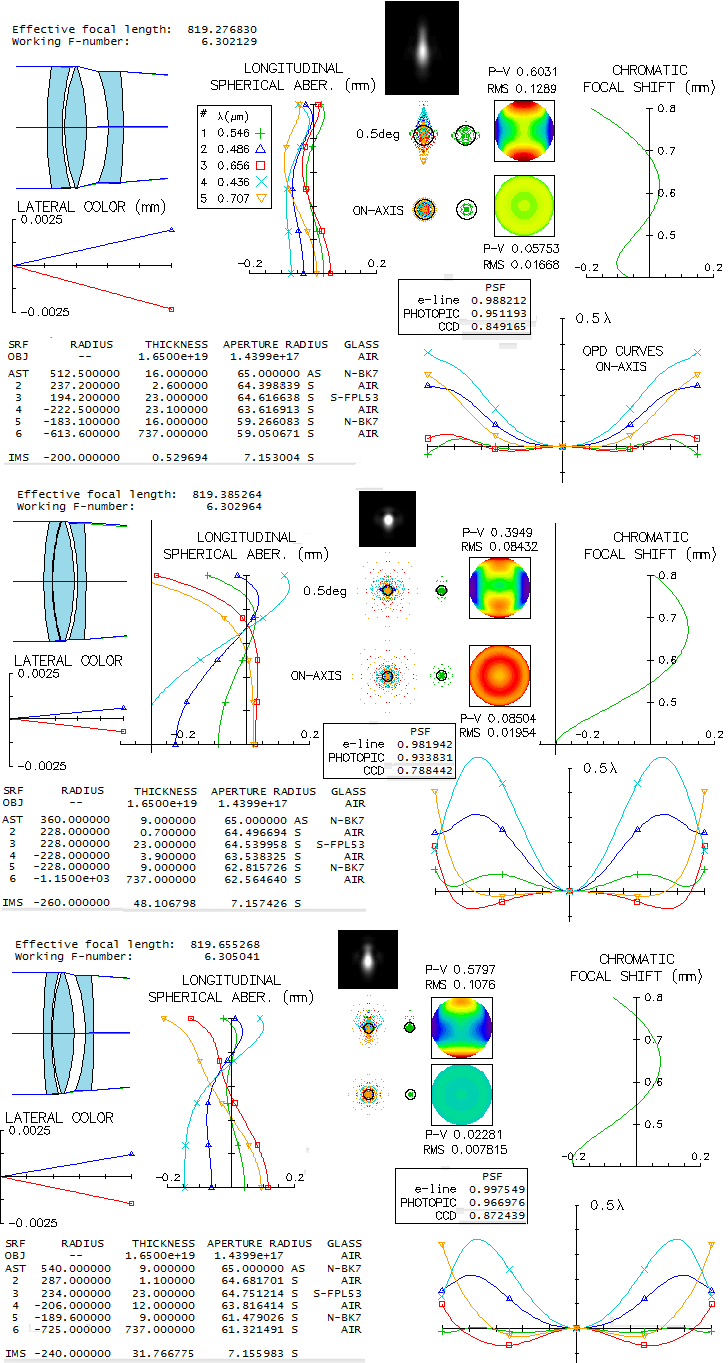
In addition to somewhat stronger astigmatism/field curvature, a price to pay
for the spherochromatism reduction is the increased lateral color, about three times
larger than in the standard triplet. Diffraction simulations show its affect at
0.5 degrees off axis, for the five wavelengths and even sensitivity. While
maybe tolerable visually, it is not acceptable for CCD. Since lateral color here
is caused by the rear gap, the only way to lower it is a reduction in the lens
separation. By nearly halving the gap, and strengthening the gap radii in order
to maintain reduction in spherochromatism, lateral color is reduced by nearly 40%,
with even somewhat higher Strehl values vs. wide gap (despite more than twice
wider LA graph span in the former; bear in mind that for any given longitudinal
error, the wavefront error for spherical aberration at the best focus location
is eight times smaller than for defocus). Note that the Takahashi TOA, due to its more
sophisticated design, doesn't suffer from a significant lateral
color error.
Spherochromatism and lens shape
Change in the lens shape also affects spherocromatism, primarily with
triplets, since doublets have their lens shape determined by
constraints related to their single gap. As an example here is
taken BSM81/FPL53/BSM81 air-spaced triplet, using Ohara super-low-dispersion glass
in combination with the closest to it on the RPD diagram lanthanoid.
This is probably a combination used for the Astro-Physics 110mm f/6
StarFire GTX apo refractor. Starting point is configuration
with all four inner radii equal, with their nominal value
determined by such needed to bring all colors close together.
In this case it is aproximatelly R2,3,4,5~210mm
(absolute value; weaker radii would bring blue-violet closer
while pushing the red end farther away, and vice versa).
However, with all four radii equal spherical aberration is grossly
uncorrected. In order to minimize it, at least one inner
radius has to be either changed, or aspherized (#1,2,3).
Also, more often than not, it is possible to minimize spherical
aberration by reshaping the middle element, while keeping the
paired radii equal. In this case, keeping them equal would
require significantly widening the gaps (#4). Keeping the lenses
in near contact requires one radius changed to correct for
spherical aberration (with every change, the first and last
radius also need to be adjusted in order to minimize coma).
Changing either R2 (#5) or R5 produces similar output, with
the former being a tad better. Changing both makes it a bit less
well corrected than either (#6). Aspherizing is, of course,
also an option, producing similar rezult (#7). Finally,
arrangement similar to #5, but having a bit better correction,
best of all variations shown (it is very similar to the design
posted on Cloudy Nights forum by RayG, only with R4 and R5
made equal, and some minor changes to compensate for the effect).

To make objectives comparable, they are nearly balanced in
F and C line, and have the central line error at near-minimum.
The first two variants, having only a single radius altered,
are less well corrected than the rest, particularly #2, mainly
because of its relatively significant higher-order spherical
residual. Aspherizing R5, with all four inner radii equal,
produces the best correction (#3), although not significantly
better than #1. Yet better correction is achieved by reshaping
middle element (#4) but the gaps required, although still
moderate, are not "near contact" anymore. Practically the
same level of correction offers its near-contact option with a
single radius changed (#5). Adjusting two radii produces slightly
lower correction level (#6), as well as aspherizing R5 (#7).
The best option (#8) has the F/C Strehl average at 0.95+, and
polychromatic photopic Strehl at 0.98. That is numerically equal
to the arrangement with somewhat wider gaps (#4), and only slightly
better than #5. No eye would be able to tell the difference (making
the rear two radii another 5mm weaker in #5 doesn't change the
poly-Strehl value, implying it is the design limit).
In all, differences in the level of correction do exist, but are
near negligible, except when there is a significant increase in
the higher-order spherical residual.
Common glass apochromats
The modern choice of glasses allows achieving apochromatic
correction in mid-range focal ratios even without the use of ED glasses.
For some reason, the market did not make a serious move to that
direction, but it could happen. ED glass is not a must for apochromatic
correction; what it requires is simply a large enough Abbe differential
and negligibly small relative partial dispersion (RPD) differential.
There is a relatively few non-ED glasses that can be used to that
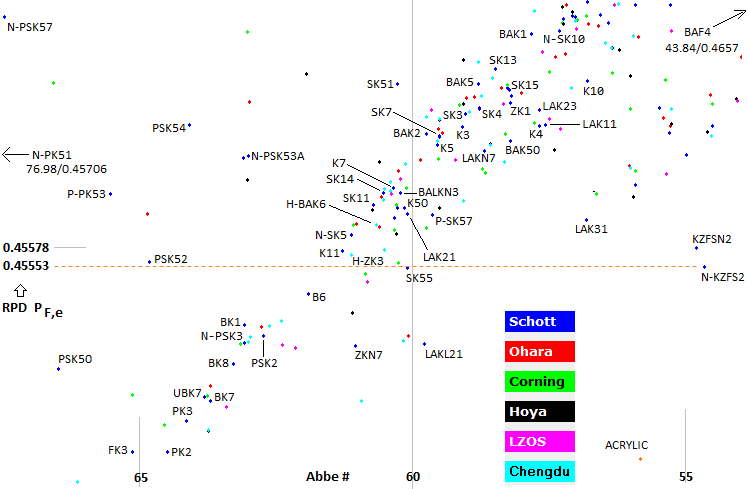
effect, and probably the best positioned is the Schott N-KZFS2 (as short-flint, not a
"normal" glass, but the main criteria here is the price, as given in the
latest OSLO Edu glass catalog). Being in the latest Schott catalog, it should have sufficient quality for
the purpose. On a diagram below, it is positioned center left. For a
more complete picture, glasses from other companies are included, but
those marked are mainly Schott, and a few others used in the examples.
Can it produce a 6" f/15 apo triplet combined with ordinary crowns like
BK7 and K5? You bet.
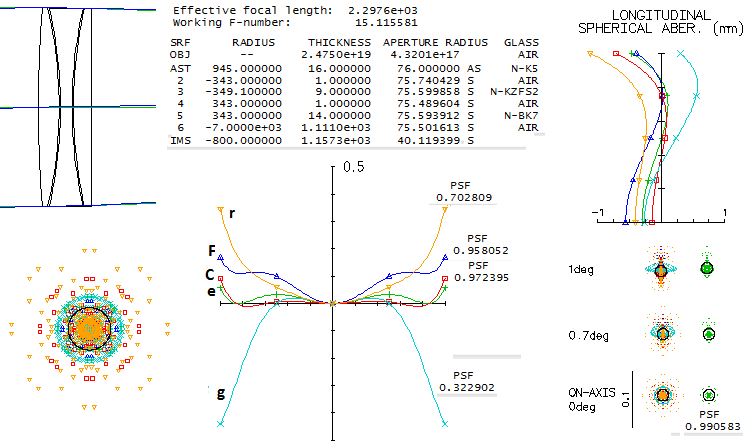
With g and r lines below λ/2, and very low error in e,
F and C, this objective satisfies the "true apo"
criterion. Average cost per glass element is 1.13 in units of the BK7
cost. The higher order spherical aberration residual can be reduced if all four inner
radii are allowed to be unequal: R1-6 1080/-424/-429/321/317/-4000, interspaces 0.65mm.
The e-line RMS goes down to 0.0065 wave (0.998 Strehl).
Similar performance can be achieved with a simpler combination, with
N-SK5.

With N-SK5 being 1.6 times the BK7 price, it comes out at 1.4 times per
lens element. Unlike the previous combination, using one matching
element with a relatively significant RPD differential and offsetting it
with the other element of similar differential of opposite sign, this
lens combine two glasses with a small RPD differential, for the
negligible secondary spectrum. If their Abbe differential was larger, it
would work with the faster f-ratios as well.
Or, going farther left, for a glass with larger Abbe differential,
would make possible faster objectives. Ohara's S-PHM53 (analog of now obsolete
Schott dense phosphate-crown PSK52) is just far enough to be border-line in an f/10
triplet, with the central line Strehl just over 0.95. But seems that going farther left
on the RPD diagram increases cost, whether a glass is with abnormal dispersion, or not.
OSLO doesn't list price for either Ohara or Schott variety, but for the CDGM analog the
price is over 8 times their BK7 equivalent. If so, better matches can be found still farther left,
such as Schott N-PK52A, listed at 7 times the N-BK7 price (this replaces N-PK51 which was
shown here before for the triplet and doublet combination; either for an error in OSLO catalog or, more likely,
on my side, it was asigned price iqual to that of N-BK7, while the current OSLO catalog has it
at 21 times more expensive). At f/8, triplet nearly passes the "true apo" minimum requirement.
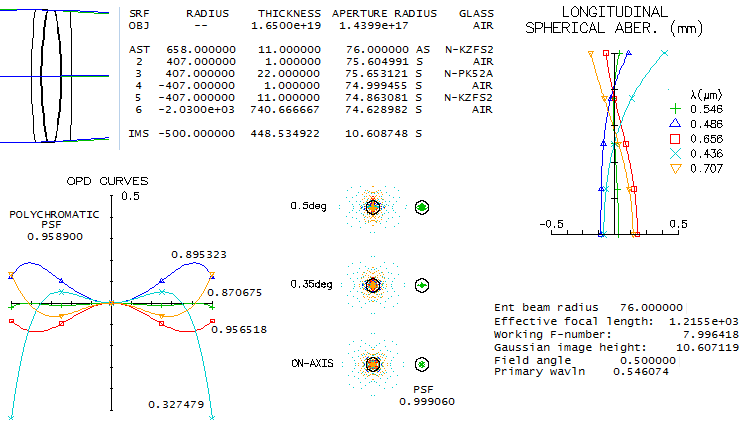
The only line somewhat running away is the violet g, but with the deep red
being significantly better than the limit, energy-wise the lens passes the "true apo"
requirement - as confirmed with its 0.95+ polychromatic Strehl.
The N-PSK52A vs. N-KZFS2 Abbe differential is large enough to work well in
a doublet too. At f/10 it has a better poly-Strehl than the triplet af f/8.
.
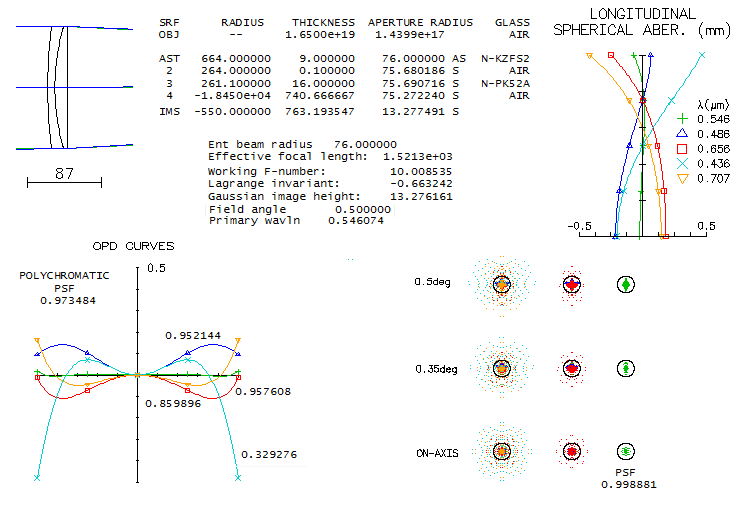
A bit farther to the left there is a very affordable ED glas, Schott N-FK51A,
listed at a price equal to that of N-BK7. Paired with N-KZFS2, it has
very similar performance to that of N-PK52A, only being a bit softer in the violet.
All at the cost equal to that of BK7 glass.
Can N-KZFS2 do it at f/12 with, say, Chinese glasses. Almost (but this
is not necessarily best possible combination, so the answer could be
"yes").
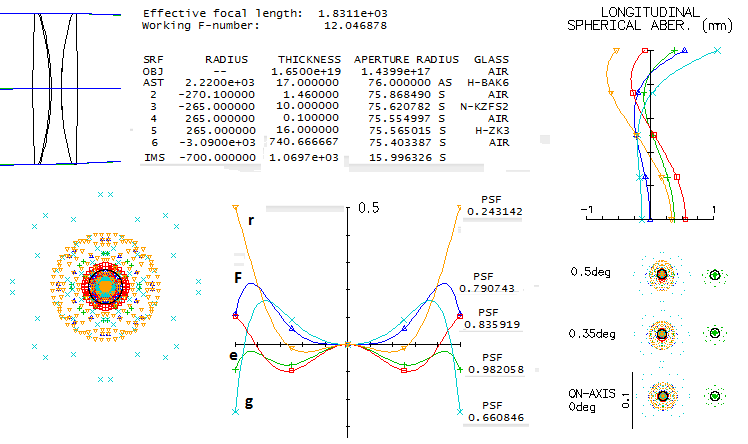
The lens is just short of the "true apo" minimum in the r and
F line. The two Chinese crowns are a bit more expensive than the
Schott's, coming out to 1.4 times the BK7 cost per lens.
Other current Schott short flints also can achieve the "true apo" level
in f-ratios faster than f/10. For instance, N-KZFS11, being somewhat
higher on the RPD diagram than N-KZFS2, does not have potential mating
glasses with as much of Abbe differential, but still can produce similar
performance level, either with glasses of a similar RPD, or combining
it with a pair of glasses of significantly different RPD differentials of opposite
sign, nearly offsetting one another for cancelled secondary spectrum.
In combination with N-SSK8, priced at 1.7 times the BK7, triplet
objective has 0.96 polychromatic Strehl at f/9, and also passes the
"true apo" g/F/e/C/r criterion.
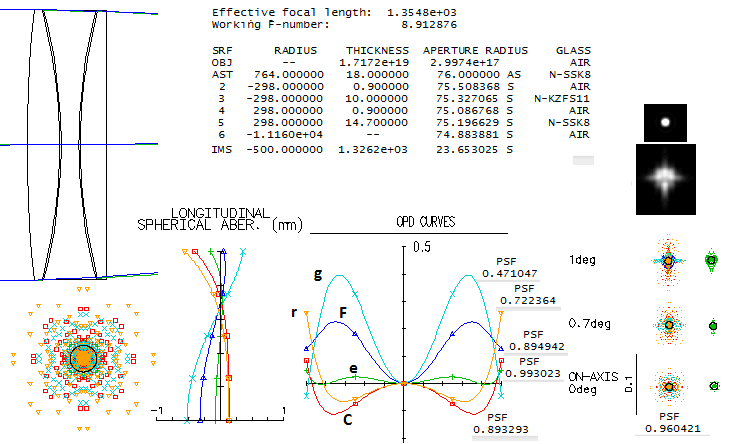
In a doublet, this combination has the "true apo" color correction at
f/15, but due to the residual higher order spherical only 0.95 Strehl in
the central line, and 0.92 polychromatic Strehl. As an example of using
glasses with significantly different RPD from N-KZFS11 that offset one
another, a N-SK5/N-KZSF11/LF5 combination has 0.934 polychromatic Strehl
at f/9, and passes the "true apo" criterion at f/10.
Dialyte apochromats
Apochromatic correction can be achieved without extra dispersion
glasses, but in general it requires widely separated lenses, in
order to generate correct sum of dispersions in the final image.
That, in turn, makes these systems longer than their effective
focal length. More disadvantages due to the wide interspaces
is that these systems are very sensitive to miscollimation
and have to meet very tight fabrication tolerances. For those
reasons, a very few of them were marketed, including Tal Apolar
and Zerochromat by Peter Wise (the well known Shuppman system was
never marketed to my knowledge, being in fact a tited elements,
broken axis design). Examples here are axial systems, with
published prescriptions (technically, Petzval systems would also
belong here, but they are already given elsewhere, since they became
relatively common).
Designs by Roman Duplov range from those using ordinary flint
and crown (two-glass systems) to those using a wider variety of
glasses, but still within normal dispersion. Image below
shows two such systems raytraced.
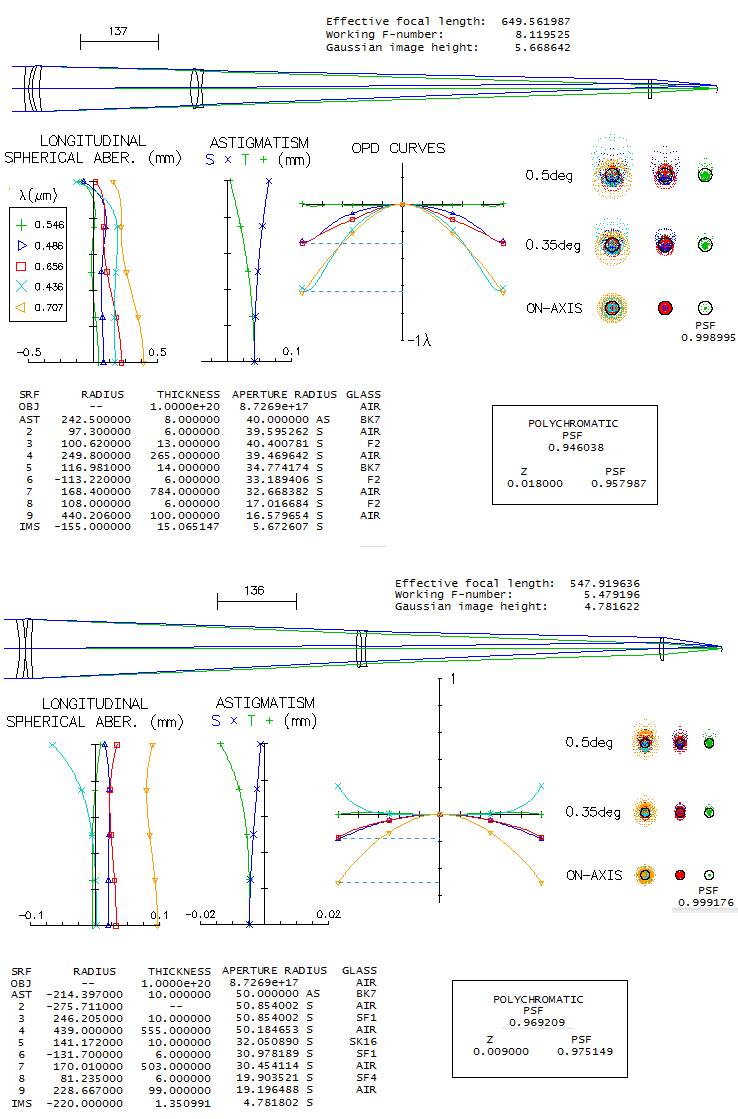
With only the common crown and flint (top) a 80mm f/8.1 system
does not quite satisfy the "true apo" P-V wavefront error
criterion in g and r lines (λ/2 wave presumably
defocus), but it does satisfy the λ/4 requirement for
F and C lines. However, it does exceed the 0.95 "sensibly perfect"
polychromatic Strehl (photopic), when defocused 0.18mm from e-line
focus). But it comes at a price of system length being more than
twice its effective focal length (note that the system is slightly
modified in order to bring F and C lines in balance).
Using more than two different glasses (bottom) allows for
better correction and shorter tube. Despite its very fast focal
ratio, the system now satisfies the "true apo" P-V wavefront error
requirements and its polychromatic Strehl at the best focus
location reaches 0.975 (note that the graphs and spots are for a
slightly changed R5, to 141.1, needed to nearly balance F and C
and to bring the r line below λ/2).
Use of ED glasses in a cost-efficient manner allows for yet
shorter, better corrected designs. Good example is 152mm f/6.5
system by Joseph Bietry, which uses FPL51 element in its
middle doublet (below; this sytem is also known as Melior apo).
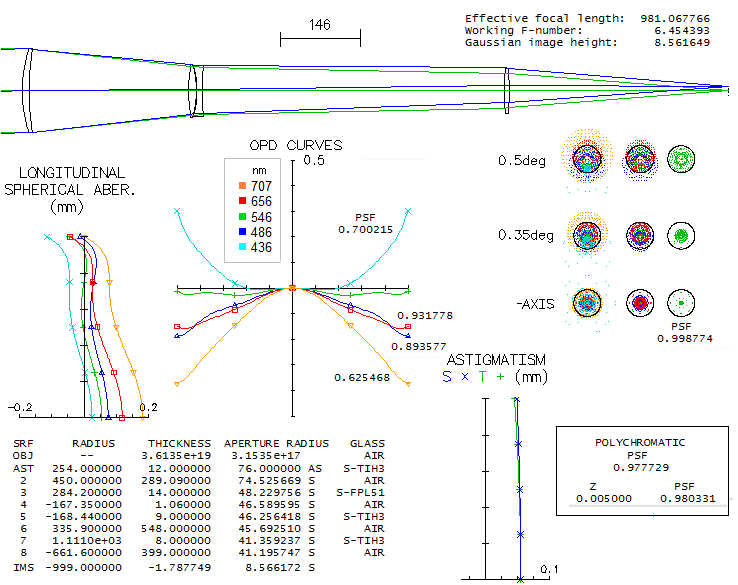
The system is more compact, safely within the "true apo" P-V
wavefront error requirements, with the best focus poly-Strehl
of 0.98 and significantly less field curvature (note that it
is also slightly changed to balance F and C -
originally it has 0.41λ P-V wavefront error in the F-line -
with R1=254.14, R2=450.6 and R7=1139.6, the likely reason being the smaller
ray spot plot). With R7=1122 it has
all colors within Airy disc up to 0.5° radius, and F and C
better balanced. The ray spot plots shown are for flat field, with the
error being still within "diffraction limited" at 0.5° off axis.
Ideally, the image field is flat. Example of such a system is
Strahov/Babaev/Mashinyan (RU 2,784,320). It employs two FPL51
elements, but the other two lenses are cheap crowns. The original
patent prescripton (below, top) uses very thick lenses, but nearly
identical performance can be obtained with thin lenses, in a slightly
different configuration (bottom).

Original design has superb correction in all wavelengths, except
violet which is lagging behind somewhat. By a slight change in lens
power violet could be improved (with the blue becoming nearly as
well corrected as the central line), at a price of larger error
in the red. For instance, with R4=348 and R2=-168.5 (to minimize
spherical aberration), the violet g-line drops below 1/2 wave P-V, with
all the other lines also satisfying the "true apo" P-V wavefront error requirement.
Design limit at 102mm f/6 is well above 0.95 photopic polychromatic Strehl,
with the best focus slightly shifted toward the F/C focus due to the
residual secondary spectrum (boxed). Mesopic polychromatic Strehl is somewhat
lower, due to the increased sensitivity in both blue and red (according
to the sensitivity model from experimental study).
The CCD polychromatic Strehl would have been still lower, and probably
a bit better for the thin lens arrangement - or, rather, for its color
correction mode - due to the average
CCD sensitivity (unlike photopic and mesopic) being higher in the
blue/violet than in the red.
_____________
Summing it up, the magnitude of secondary spectrum is only a part of the
equation - and not necessarily the most important one - when it comes to
the chromatic correction level of refracting objectives. Its existence
itself does not prevent achieving sensibly perfect chromatic correction.
Even the standard achromat will do if left long enough, and it only gets
easier with glass combinations that have it reduced or even eliminated.
But as the secondary spectrum diminishes, another chromatic aberration -
spherochromatism, or variation of spherical aberration with wavelength
(also called tertiary spectrum) - takes the front seat. In
general, it increases exponentially with the relative aperture (D/f),
and in proportion with the aperture diameter. Thus, a zero secondary
spectrum does not necessarily mean great chromatic correction, and
could, in fact, accompany a less than perfect, or sub-standard one.
Similarly, the number of color crossings itself does not guarantee high
level of correction. It does imply that the wavelengths over the visual
range are packed tightly together, but what will ultimately decide the
level of chromatic correction is the magnitude of spherochromatism. And
it is, at any given focal ratio and aperture, mainly determined by the
form of objective (doublet, triplet, quadruplet, Petzval) and Abbe
differential of the glasses combined.
Using adjective apochromatic in any form to imply the level
of chromatic correction is fundamentally inappropriate, since its
primary meaning is for the specific mode of chromatic correction.
Apochromatic objective can be poorly color corrected and, on the other
side, standard achromat can be sensibly perfect. Does that make them
"fake apo" and "fake achromat"? Of course not. They still have those
same respective modes of color correction. What determines their actual
error level is not their color correction mode, but the size of
aberration over the wavelength range. And it should be expressed in the
standard form for all aberrations, the RMS wavefront error and Strehl
ratio. Combined with the particular spectral sensitivity of the
detector, they determine the actual diffraction intensity at the focus
point, the polychromatic Strehl. According to generally accepted
criteria for visual observing, refracting objective is sensibly perfect
if its polychromatic Strehl exceeds 0.95.
◄
9.2. Refracting telescope objectives: Apo
and semi-apo
▐
9.3. Designing doublet achromat
►
Home
| Comments |











