14.3.RAYTRACING OBSERVATORY TELESCOPES

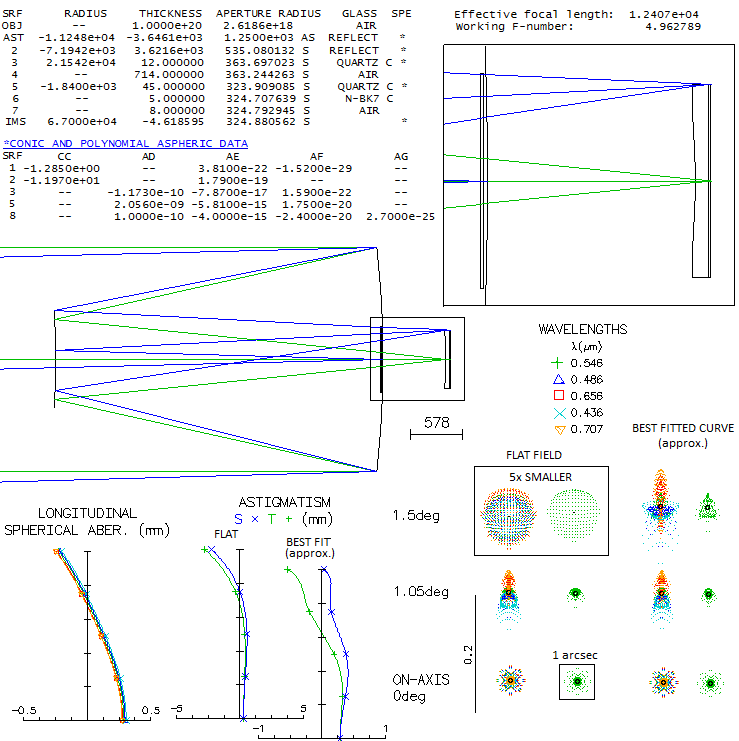
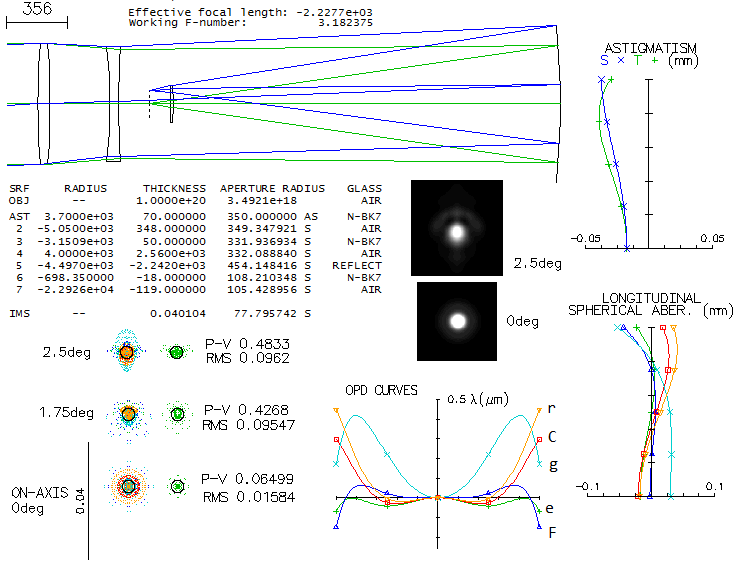
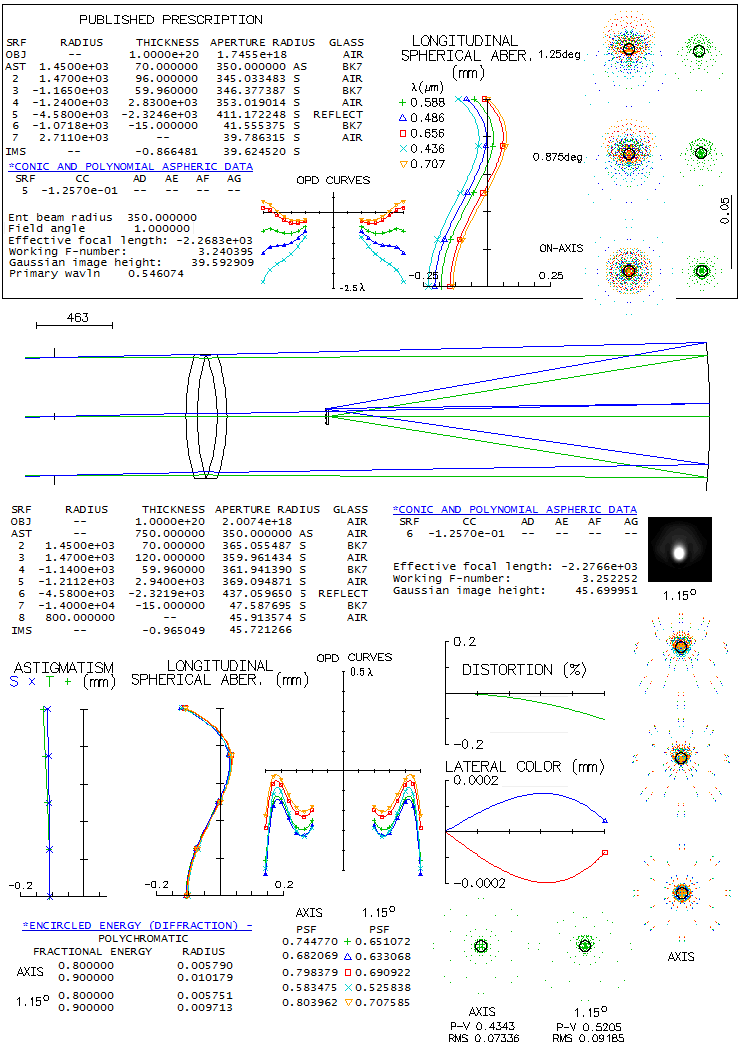
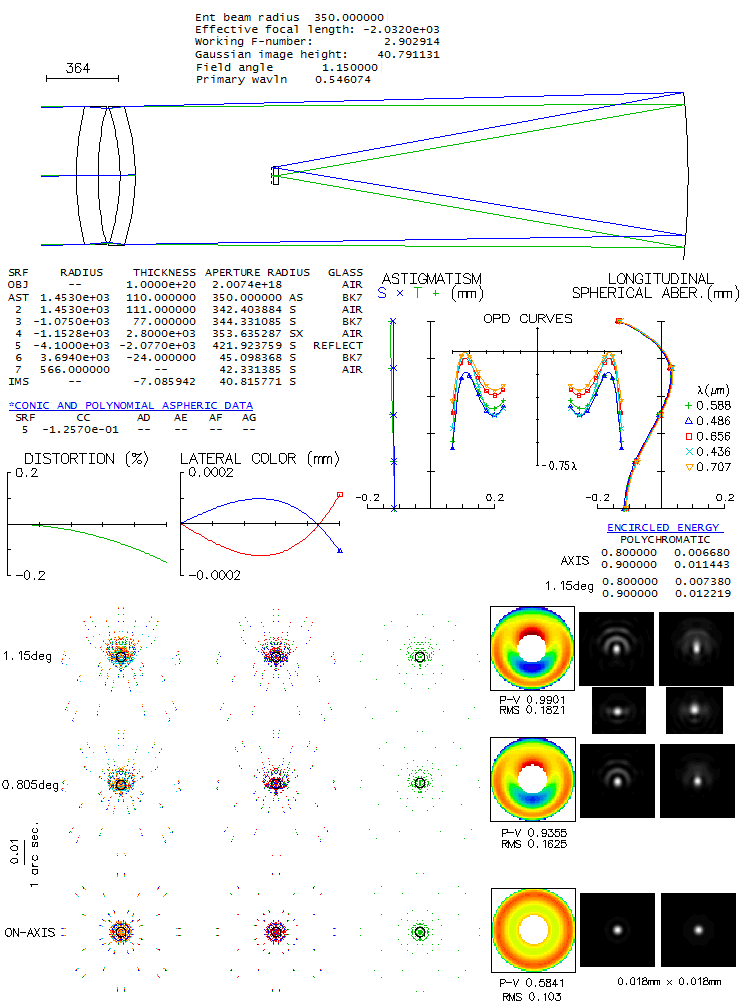
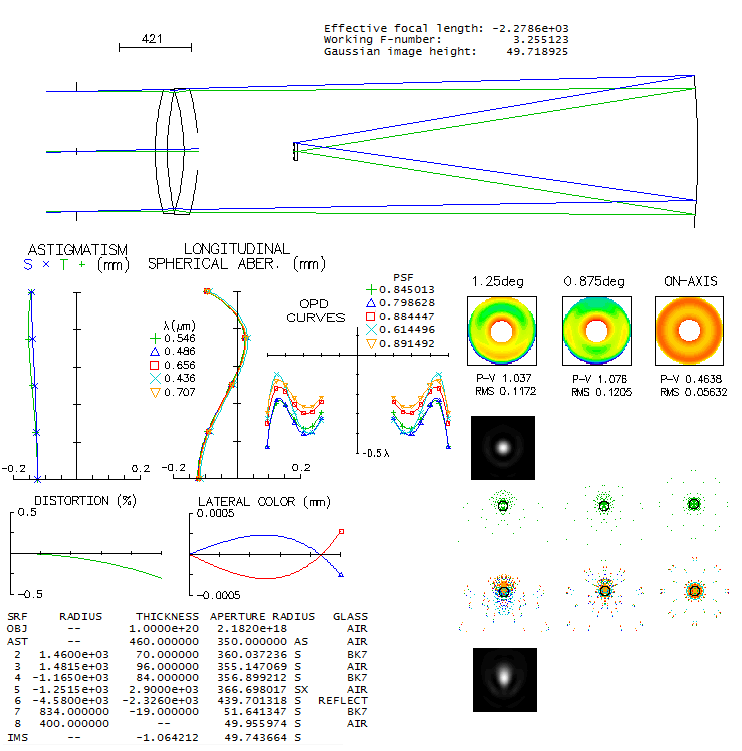
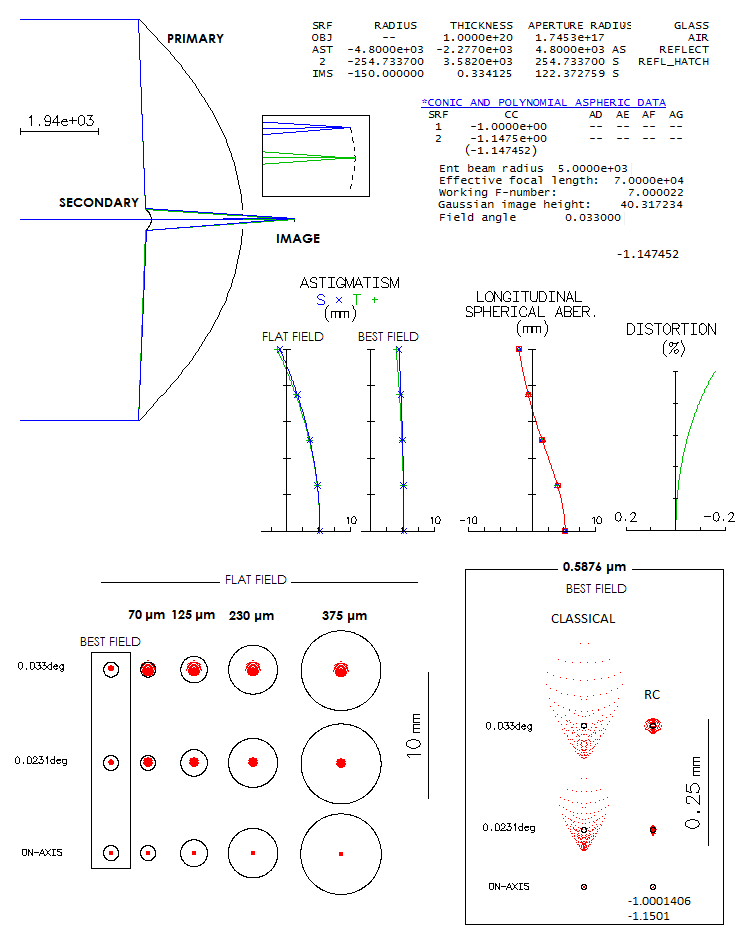
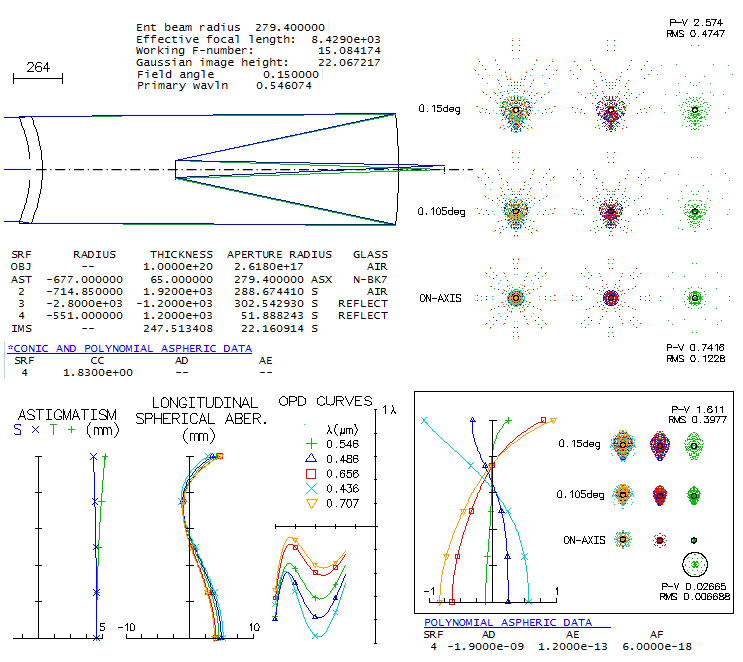
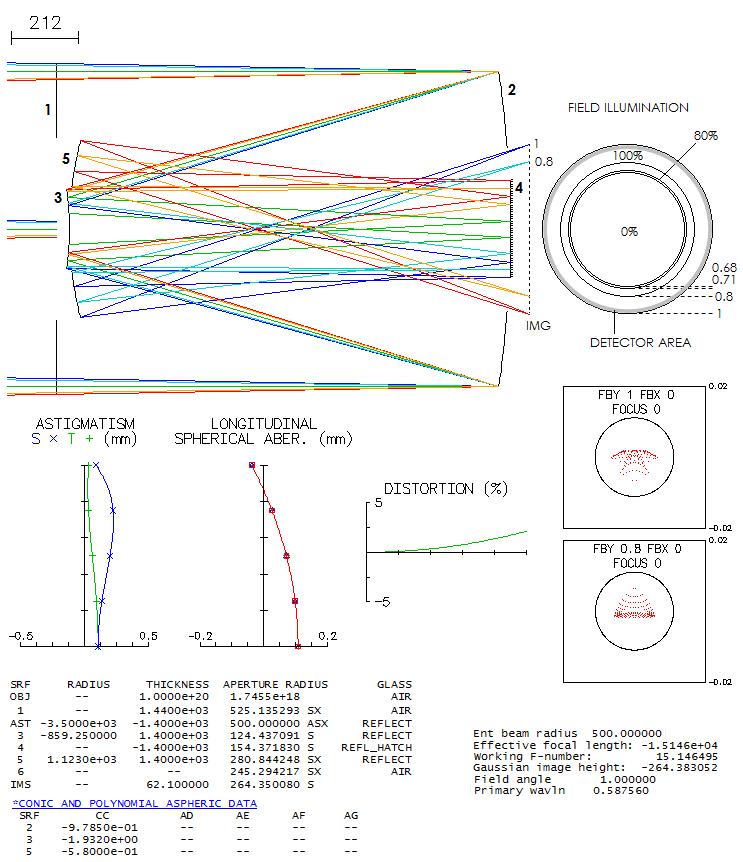
Arguably one of the best corrected simple systems is the three-mirror system known as Paul, or Paul-Baker telescope. So when a group of astronomers from the University of Arizona's Steward Observatory were looking for a very large, ultra-fast widefield design for the Dark Matter Telescope project, it led them to the Paul-Baker, since no two-mirror system, or a Schmidt-like telescope, could achieve the needed level of correction. The telescope would be limited only by atmospheric seeing and sky background photon noise, which means it has to produce star images smaller than 0.5 arc seconds, achievable occasionally with large telescopes on best sites. The goal was the largest telescope possible with 10m focal length, needed for sufficient sampling with a 15-micron pixel (1 arc second=51 micron).

Their first design, a 6.5m f/1 Paul-Baker telescope with all three mirrors aspherized in Zemax, was capable of producing required image, but had suboptimal plate scale, and unacceptable chromatism from the dewar window. That led to the revised design, a 8.4m f/1.25 telescope with a curved dewar window and added correcting lens. This design was the starting point for the 8.4m f/1.234 Rubin Observatory Simonyi Survey Telescope (El Penon, Cerro Pachon, Chile), with even wider, 3.5-degree field, and a bit better correction (less than 0.3 vs. less than 1/3 arc seconds design image). Since there is no prescription for the Rubin telescope, the University of Arizona's design will be used to illustrate this, we could say unique kind of a telescope. Unfortunately, prescription given in the paper isn't working, but a system with comparable performance can be reconstructed from it.

The main parameter of optical performance is ensquared energy. It is given on the bottom of every 1-arcsec square containing ray spot plots for the 0.80 energy square all values are in meters, so the 7.77^-6 for the axial e-line 0.80 energy square is 7.77 microns). At 1.5 degrees off axis the polychromatic 0.80 energy square side is 24.9 microns, or nearly 0.5 arc seconds. It would probably be the subject of final optimization, generally by near-equalizing error over the field, by allowing more of an error in the inner field. At 1-degree off, the 0.80 energy square is 1/3 of arc second, becoming significantly better toward axis. Astigmatism is minimized, near zero at 1.5 degrees off, with the dominant aberration there being trefoil.

The small dot in the center of each box is the Airy disc; entirely irrelevant here, but illustrates the magnitude of aberrations in this highly corrected large telescope.

More complete picture of the aberrations is given by the Zernike terms. The main contributors are in red (piston is not an aberration in the single-aperture system, just a nominal artifact, and the defocus value - which translates to 0.33 wave RMS, i.e. 1.16 wave P-V - is evident on the astigmatism plot (best focus is not necessarily where astigmatism is at its minimum; in the presence of other aberrations it can shift to another location).

The largest single contributor is trefoil (#9). The next highest one, quadrafoil (#16) is already near negligible, adding only 15% to the trefoil (because Zernike terms add up as square root of their squared values), and even less considering secondary trefoil (#18). Most of the terms are negligible individually, but do have significance as a total, creating a higher-order aberration "noise" in this large and fact telescope.

At 1 degree off axis dominant aberration is astigmatism, but it is significantly smaller than what the longitudinal aberration graph indicates (nearly 6 waves P-V, from W=L/8F², L being the longitudinal aberration, and F the system focal ratio). The reason is that a mix of lower- and higher-order astigmatism of opposite signs has up to four times lower error at the best focus for given longitudinal aberration, and that large central obstruction also lowers the error.

2 - SDSS TELESCOPE: 2.5m f/5 MODIFIED RITCHEY-CHRETIEN

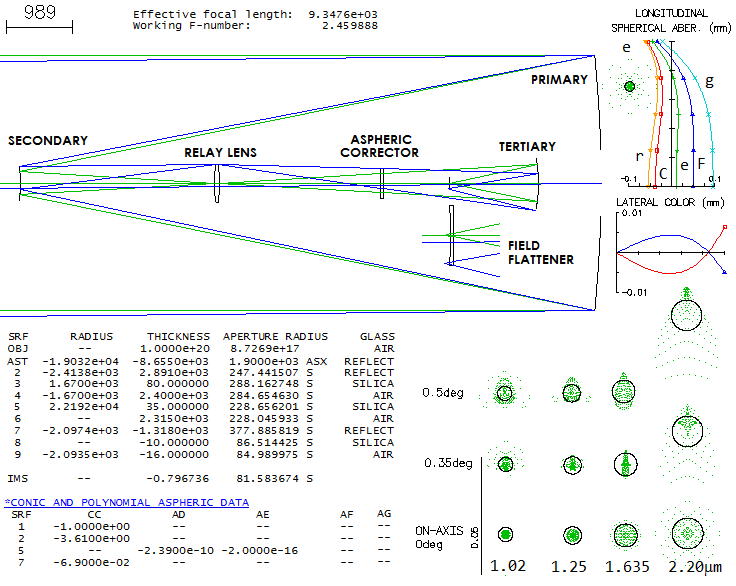
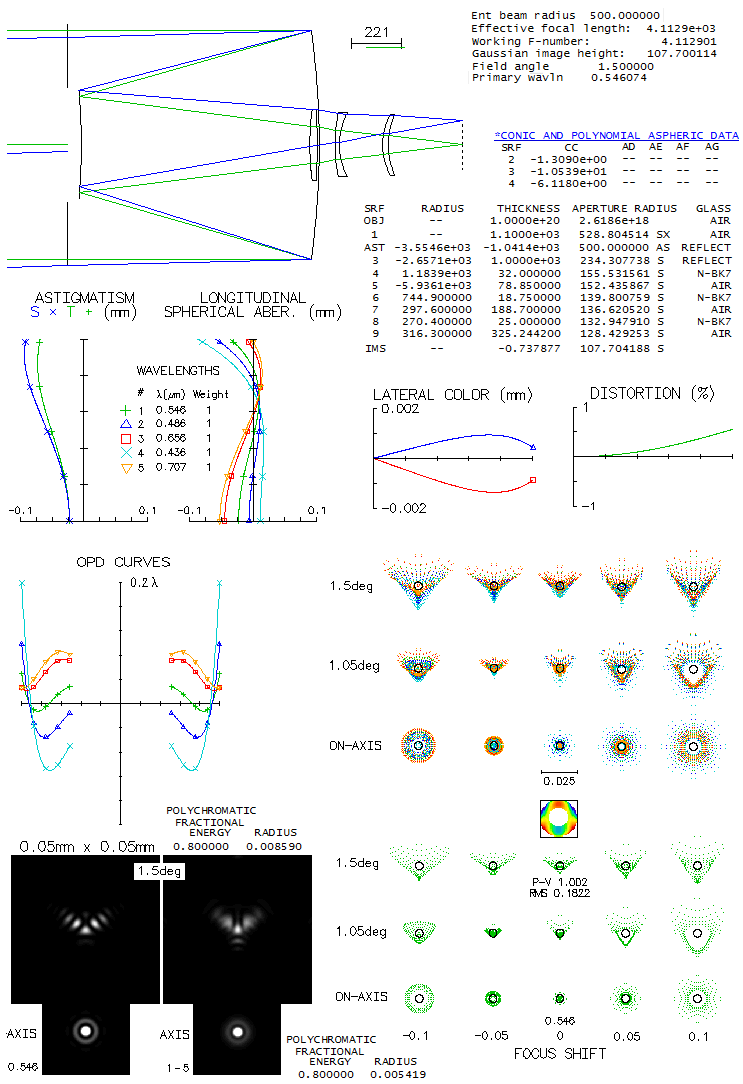
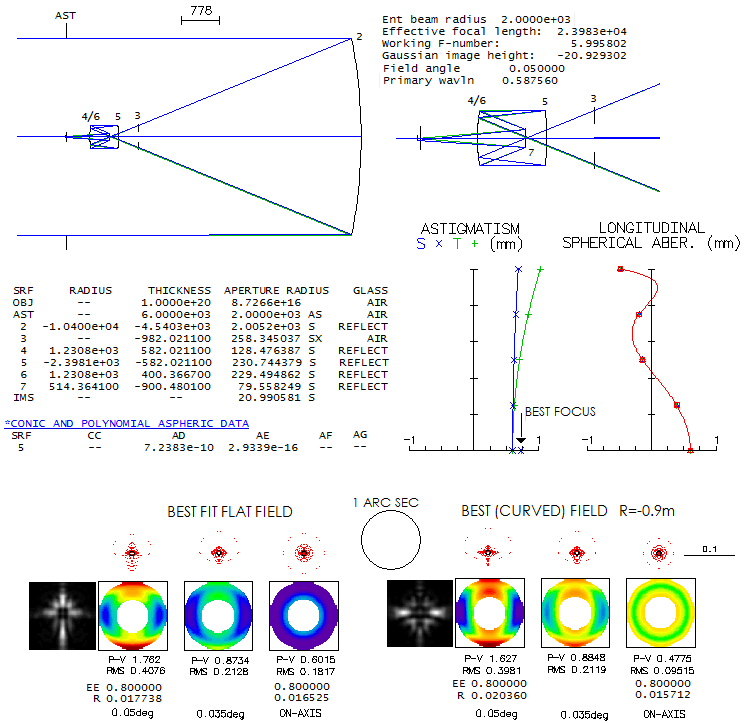
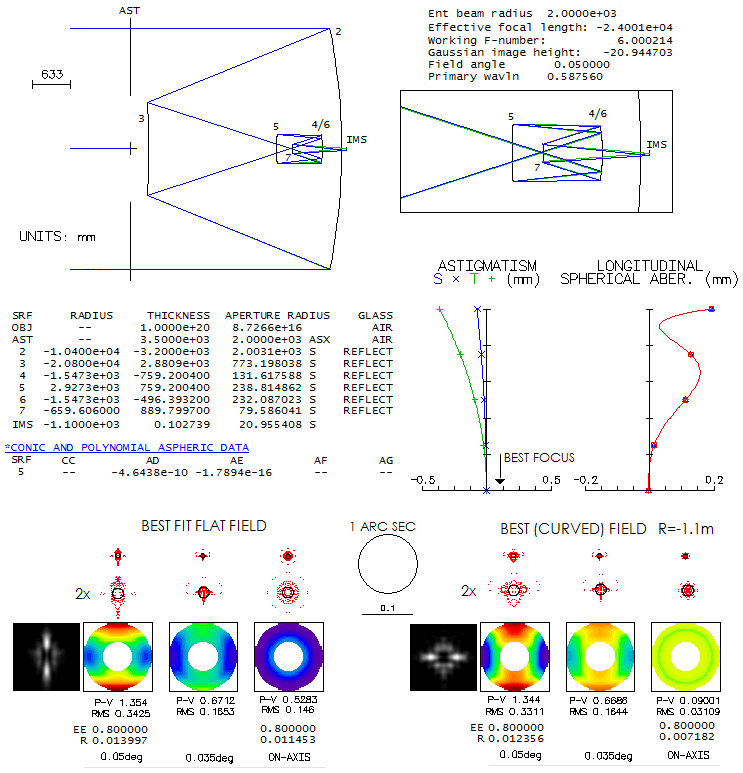
Located at Apache Point Observatory in New Mexico, the main tool of the Sloan Digital Sky Survay project, this telescope uses a two aspheric lens field correctors to achieve a well-corrected 3-degree field. As described in paper by Gunn et al. its second corrector lens is interchangeable, allowing it to be optimized for camera and spectroscopic mode. It is used to map the depths of our Universe.

The two corrector lenses have their radii given indirectly, through the value of a2 coefficient, whose full expression is a₂=d²/R[1+(1-K)(d/R)²], with d being the the surface radial height, R the radius of curvature and K the surface conic. It is not clear why, because the surfaces are spherical (K=0), and (d/R)² is negligibly small, especially for the first corrector, hence for all practical purposes a₂=d²/2R, and R could be expressed directly (for the second corrector, it would give about 3% longer radius, but it would have little consequence).

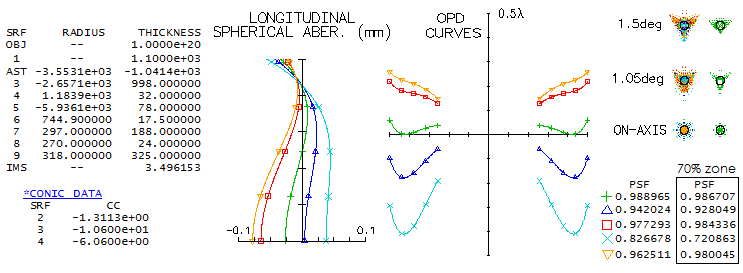
Raytracing the prescription for camera mode shows, perhaps, less than expected correction-wise. The field is, as described in paper, nearly flat up to about 80% of the 1.5-degree radius, curving inward rather strongly after that. Color correction is good overall, but widely separated lines show significantly different forms of aberrations toward field edge, i.e. their best foci do not coincide. One of the requirements was near-zero distortion; according to OSLO, it just exceeds 0.1% at the field edge.

The outer portion of the field required adjustment of the detector shape. It cannot be fitted with a near-spherical curve, and requires higher order aspherics. Here, the asherics are combined with 67m curvature, which resulted in a good, but still someone uneven fit (the edge is for the best green focus; the red becomes roughly round at 99m curvature, but green out of best focus).

The paper gives no specific performance criteria for the camera mode. Final images were calculated as convolved with 0.8 arc seconds seeing FWHM, which proved to be too optimistic. For the system focal length, one arsecond is 60 microns. On the fitted field, the green line 80% energy square is 18.7 microns on axis, 15.5 microns at 1-degree, and 35.8 microns at 1.5. It indicates that the seeing is limiting factor, rather than optics.

Full spectral range of the telescope is 0.3-1 micron, but the familiar visual 0.43-0.70 range well illustrates its chromatic correction.

3 - EELT: THE 39m, LARGEST-EVER-TO-BE OPTICAL TELESCOPE

European Extremely Large Telescope is designed as a three-mirror anastigmtic aplanat. As described in a paper by Cayrel, the 39-meter f/0.93 ellipsoidal primary consists of 798 hexagonal segments, each 1.45m across. The 4.2m convex secondary and 4m concave tertiary are each a thin meniscus. All three mirrors are active: the primary to make possible for it to conform to the proper shape, and the other two - particularly tertiary - to correct wavefront errors, mainly those caused by atmospheric turbulence, but also those caused by mechanical deformations.

Two folding flat mirrors direct light beam to the side (Nasmyt focus). The first, 2.5m in diameter, is also active, "specified to deliver near infrared diffraction limited images with over 70% Strehl ratio in median atmospheric conditions (0.85 arcsecond seeing, t0 of 2.5ms)". The second flat, 2.2 by 2.7m, corrects for tip-tilt errors. 

Field radius is nearly 5 arc minutes, limited by the central hole in the fourth mirror (even such a small angular radius produces almost 1m image radius). The prescription gives a final f/16.6 system, somewhat faster than f/17.5 cited in the paper; not sure what is causing the difference, but the design correction level is very high.

Even at the field edge, correction is still at the level of 1/12 wave P-V of lower order spherical aberration. With the ~660m focal length, one arc second at the detector is whooping 320 microns - about 1/3 mm. The only significant aberration is field curvature (ray spot plots shown are for the best image surface, of 11.2m radius; on flat field, error at the 5 arc minutes field angle - i.e. 0.94m off center - is as much as 30 waves P-V of defocus).

4 - THE 40-inch YERKES AND 36-inch LICK REFRACTOR

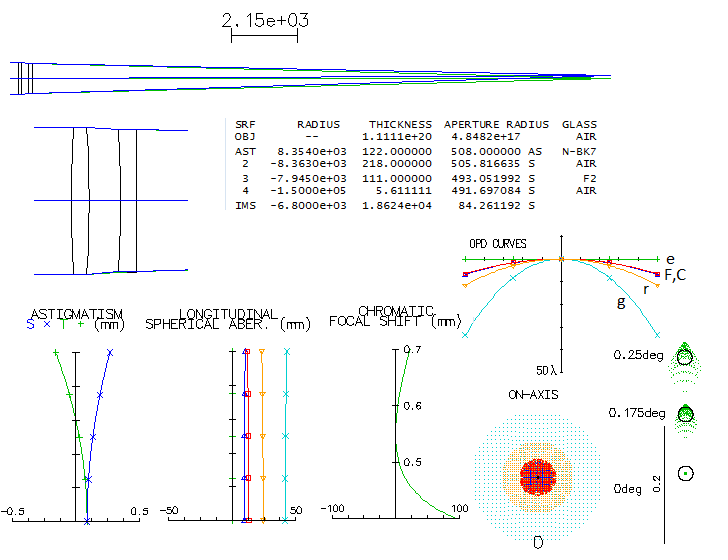
Keeping in the company of the largest - ever wondered how much chromatism there is in the largest refractor ever built: the 40-inch Clark refractor at the Yerkes observatory in Wisconsin? It is a common crown/flint achromat; according to the most relaxed criterion (Sidgwick), its focal ratio for acceptable (roughly 1/4 wave level) color correction should be f/120 - and it is f/19. I was always curious, just how much of color this quarter tone of achromat glass generates. Using general data on the Clark doublet, and Barnard's measurements, gives following picture.

On axis, Airy disc is a barely visible dot in the center of defocused C (656nm), F(486nm), r (706nm) and g (436nm) lines. The F/C error is nearly 7 waves P-V, which puts it at the level of a 100mm f/1.8 achromat. At the field edge, coma is nearly three times the Airy disc - or 0.8 waves P-V - visually unnoticeable (about f/16 paraboloid level). As a side note, Yerkes refractor actually is not the largest ever built. It was the 48-inch (122cm) refractor built for the Great Exhibition in Paris in 1900. It had 57m focal length (f/46.7), so it used siderostat mirror to reflect light into immovable objective lens, with the focuser in a form of a carriage on rails. With thermal issues and bad location on top of that, it performed poorly and did not attract buyers. The Yerkes refractor - the idea of George Ellery Hale, paid for by Charles T. Yerkes and becoming a telescope in October 1897. - is the largest ever used as a full-capacity astronomical telescope. Now, as it is not in use anymore, the largest used refractor is its 36-inch f/19.3 cousin at the Lick observatory. So let's take a closer look at this second largest refractor built by Alvan Clark & Sons.

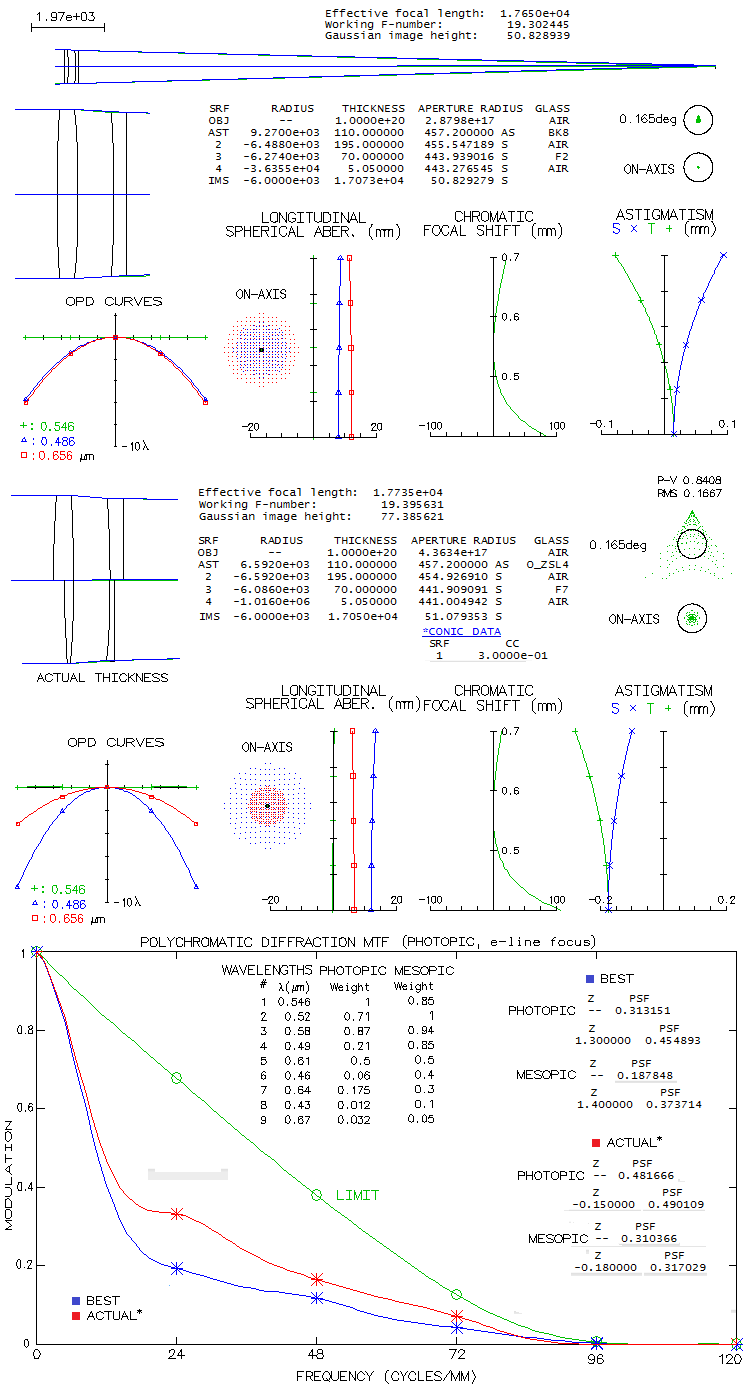
The James Lick Telescope was built nearly a decade before the 40-inch, in 1888. According to a brief description by its maker, it consisted of a biconvex crown 1734 front lens (n=1.52), and a negative meniscus of flint 1588 (n=1.64) as the rear element (Note on the loss of light in the 36-inch Lick objective, J.H. Moore, 1904.). Lens radii are specified, but the separation is not, so it will be assumed as nearly proportional to that in the Yerkes refractor (comes to ~195mm; some sources state as little as 25mm, but it is highly unlikely, since the main purpose of the gap was to make possible lens maitenance w/o having to take front lens out). The lenses were exceedingly thin - 1.98 and 0.93 inch center - for a few good reasons (light transmission, weight, glass homogeneity) - but it certainly didn't help figuring accuracy. Raytrace below uses less thickness comparable to those used in the Yerkes refractor raytracing, but it is of little significance for the raytracing output. First is presented such design with the standard achromat glasses of this era, with balanced F/C aberration, corrected for coma (top), and then the actual objective - i.e. nearly as close to it as reasonably can come - below (O-ZSL4 is an obsolete Ohara krown; very similar output is produced by the Schott K3 crown).

The first, contemporary correction mode results in a defocus ranging from some 22mm at the 0.7 micron wavelength to zero in proximity of e-line and to 86mm at 0.4 micron wavelength. In the blue (F-line) and red (C-line), defocus is evened up at about 6 waves P-V. Monochromatic aberrations are negligible across the field 1/3 degrees in diameter, over best image surface of 6m radius (it is still well within "diffraction limited" at 0.165° off flat field).

However, according to measurements, the actual C focus of the Lick refractor is midway between its "minimum" (i.e. optimized, 0.565 micron wavelength) and blue (F-line) focus (On the chromatic aberration of the 36-inch refractor of the Lick observatory, J.E. Keeler). If so, the error on the blue spectral end becomes significantly larger, while smaller on the red end. An MTF graph (photopic, for the e-line focus) showing the respective contrast levels is surprising at first: it shows significantly better contrast for the actual correction mode, favoring the red end (nominal cutoff, probably due to the short wavelengths lingering just above zero, is significantly higher than the practical cutoff, which is somewhere around 100cpm). However, it is not too hard to see that it results from the significantly lower photopic sensitivity to the blue/violet end. Also, with achromats generating significant secondary spectrum, best diffraction focus is always shifted from the optimized focus. In this case, the shift is much more significant with the first, balanced correction mode, but even at the best photopic focus its polychromatic Strehl is still somewhat lower than for the Clark's lens: 0.455 vs. 0.490 (focus shift in mm is under "Z"; zero focus shift represents the e-line focus).

For the complete picture, however, both lenses also have to be measured against mesopic sensitivity, since during night time observing eye sensitivity shifts toward that mode. While there is no accurate data on the actual mesopic mode sensitivity (the official version merely takes the average between photopic and scotopic), it can be approximated from experimental studies. The sensitivity is, in general, higher on both ends of visual spectrum (and lower for the photopic peak), but more so on the blue/violet end. The result is that the balanced mode now have higher mesopic poly-Strehl than the Clark's lens: 0.374 vs. 0.317. It indicates that the actual Lick refractor lens performs better with eye in photopic mode, but becomes inferior in the mesopic mode. This level of chromatism is roughly comparable to that in a 100mm f/3 achromat.

With respect to monochromatic aberrations, the original lens had sigificant spherical aberration residual (reportedly, about two waves P-V), and had its front surface aspherized at a later time in order to have it corrected. This arrangement (Clark's radii prescription with the glasses closely matched) has, if all-spherical, 1.5 waves P-V of overcorrection. It could be corrected by changing R3 to -6295mm, but it would throw color correction out of balance (blue F-line focusing about 2mm before e-line, and the red C-line 19mm beyond e-line focus), so it would require regrinding/repolishing of at least one more surface. Aspherization of the front surface is much simpler, in this case requiring 0.32 conic (oblate ellipsoid).

5 - 1m KLEVTSOV-CASSEGRAIN VARIETY (Vihorlatska Observatory, Slovakia)

In his book "New serial telescopes and accessories" (2014), Klevtsov gives prescription obtained from the Slovakian observatory, as a big-scale example of a telescope of the Klevtsov type.

The telescope was made in Odessa, SSSR. Original prescription is with BK7 glass (i.e. K8, its LZOS analog), but K7 glass reduces longitudinal error in the blue/violet to less than half, so that this 1-m telescope easily passes the "true apo" requirement. As with every system of this type, dominant aberration is off axis astigmatism.

6 - 0.7m 5° HOUGHTON-TEREBIZH SURVEY TELESCOPE

One of many designs of Valery Terebizh, the Russian "master designer" as referred to by M.R. Ackerman, is a simple Richter-Slevogt (known as Houghton on the Western side) modification with widely separated corrector lenses, making possible significantly wider fields. Survey telescopes are usually of relatively small apertures, with large corrected field being the primary concern, but larger apertures can be needed for detecting fainter targets.

The Houghton-Terebizh offers 5-degree field at f/3.2. The system shown is slightly tweaked to have the axial error minimized (at no expense to off axis performance).

 Color correction even at this aperture size and relative aperture passes the "true apo" criterion. The 80% energy square is 6.6 microns on axis, and 8 microns at 2.5 degrees off (diffraction images are for the 5 wavelengths with even sensitivity).

This design can also be used as a typical survey telescope, smaller in size and faster. If rescaled to 350mm aperture and f/2.4 focal ratio - parameters of a telescope of this design used in the gamma-ray burst system observatory near Moscow, Russia (The Mobile Astronomical System of Telescope-Robot) - it still preserves a very satisfactory performance.

Note that the actual telescope is somewhat shorter, with the corrector lenses more widely separated and with the final image that would form behind the rear corrector lens, if not directed to the side with a diagonal flat).

7 - 3.8m f/2.5 UK INFRARED TELESCOPE

While designed for work outside the visual spectrum, the UKIRT is based on unusual relay lens design which, with minor adjustments, could be used in the visual range as well. Here is presented its Wide Field Camera mode, as described in this online paper.

System is simplified by omitting optical window and filters, which has a minor influence on its output. The entire field covers 0.93-degree diameter, but the actually used are only four rectangular portions of it, as illustrated in the paper. The telescope is optimized to operate in four IR ranges: Y (0.97-1.07 microns), J (1.17-1.33), H(1.49-1.78) and K(2.03-2.37). As given here, the is somewhat biased toward the lower three, possibly the consequence of omitting mentioned elements.

Sub-aperture aspheric plate helps correct not only spherical aberration, but also coma and astigmatism.

The ray spot plots are given for the central line of each of the four wavebands, when refocused to their respective best focus. Above right are plots for this same system in the visual wavelengths (focused on e-line). Only minor optimization is needed to have it perform satisfactory as a visual telescope.

8 - 8.4m f/1.24 SIMONYI SURVEY TELESCOPE

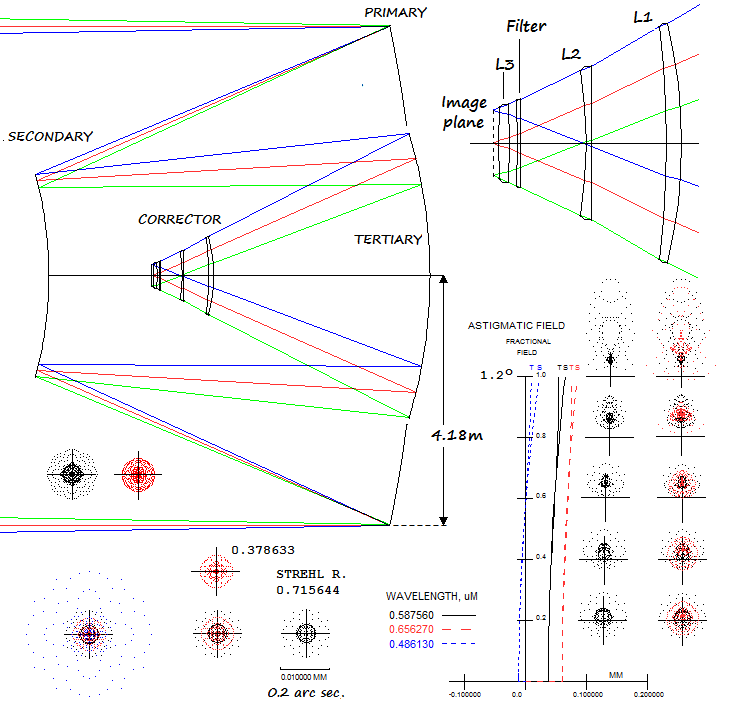
The Large Synoptic Survey Telescope (LSST), a compact version of the 8.4m telescope on the top of this page, is one of a kind, in that it sports etendue - as a product of its clear aperture and field area - of 318m²deg², over 50 times more than the first next contender. Located on the Cerro Pachon, Chile (60 miles from La Serena), this modified Paul-Baker, or Laux telescope uses three mirrors and a 3-lens corrector to produce a 3.5-degree field diameter with less than 0.2 arc seconds (0.01mm) FWHM star images over its 0.63m diameter detector, with over 3 billion 10-micron pixels. In 5 spectral bands from 400-1030nm it will be used to create by far the most complete picture of the solar system, Milky way and transient optical sky, as well as for exploring dark energy and dark matter.

Based on the published prescription (LSST Camera Optics, Olivier et al, 2006), I raytraced design with SYNOPSYS (free edition). Despite the prescription being unclear in some istances - namely, not specifying front radius of the second lens, what is the filter substrate, and to which surface of the second and third lens were applied given conics and higher order aspherics, the assumed choices - flat 2nd lens front surface, aspherics on the front radius of the 2nd and 3rd lens, filter made of BK7 glass - produced performance level sufficiently close to the description (the only change was in the value of the 6th order aspheric coefficient on the second lens front radius, to 1e-19). It is possible that some other choices would work better.

The field is limited to 1.2-degree radius, when definition begins to deteriorate; but even at 1.75° the condensed core of the roughly four times longer blur (the width is about 0.025mm) is about 0.02mm long by 0.007mm wide, or 0.4 by 0.14 arc seconds. No effort has been made to optimize either axial or edge performance, but there is certainly room for it. Should be noted that this particular setup is optimized for R-bend (red); the blue line is given only to illustrate the overall correction in this particular mode; in its optimized setup, it is further corrected by filter shape and small changes in lens spacing, and should be at the similar level as the red. Despite the prescription being optimized for the red, this take on it still has better correction in the d-line (despite the red blur appearing somewhat smaller, it is more compact, and significantly larger than the dense core of the d-line ray spot, as better show spots above with twice as many rays; note that the ray spot size for highly obstructed aperture is significantly larger than for unobstructed one, for any given level of spherical aberration).

This version of SYNOPSYS doesn't give encircled energy, which would be the best measure for verifying the actual energy spread at any field point, but the size of ray spot plots does confirm, qualitatively, that the field is corrected to FWHM better than 0.2 arc seconds (0.01mm). Another useful indicator of performance level, MTF, shows that better part of the contrast loss comes from the aberrations in the low frequency range, and from the 0.60D central obstruction in the mid-frequency range. In the high frequency range, the telescope performs

slightly better than perfect aperture (MTF plot for 1° off axis roughly coincides with the axial plot). The actual MTF, however, is obtained by multiplying the system MTF with the pixel MTF. Since the 10-micron pixel here is somewhat larger than the FWHM in absence of seeing error, the actual MTF would be lower approximately by a sin(νπ)/νπ factor, with "ν" being the MTF frequency. Since this large aperture even on the best sites will have a substantial seeing-induced error, the pixel MTF degradation factor will likely be superseded by seeing (i.e. the seeing FWHM will be significantly larger than the pixel, reducing pixel MTF degradation to negligible).

9 - HUBBLE SPACE TELESCOPE

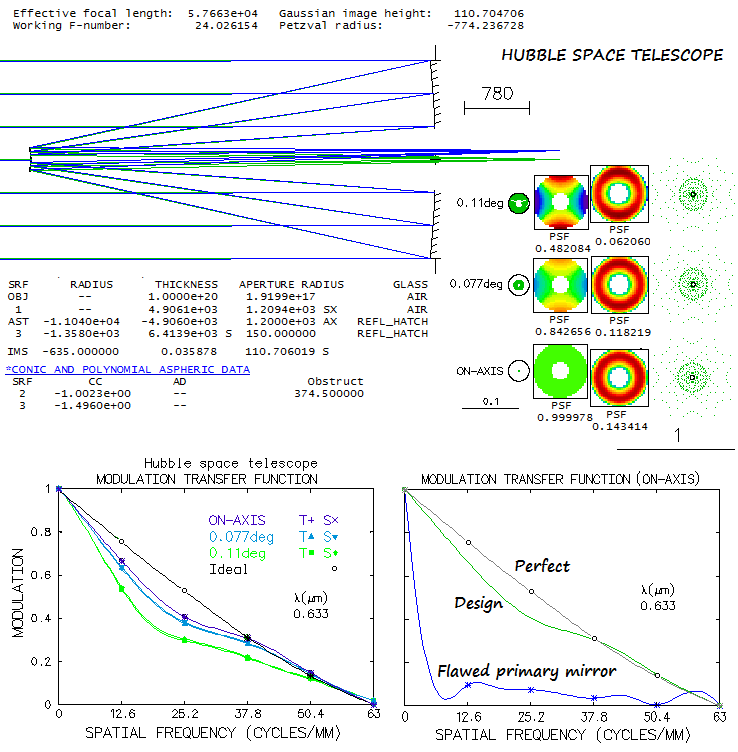
As NASA brings our space eye back to life, it warrants taking another look at it. This 2.4m f/24 Ritchey-Chretien system could, with only two perfect conic surfaces, achieve perfect axial corection. The real instrument, after accounting for non-figure errors (i.e. smaller than 1/10 of the mirror diameter), as well as <0.01 arc second pointing error, expected to deliver 1/20 wave axial RMS, or better. Off axis, limiting aberrations are 0.63m field curvature and astigmatism, with the latter limiting "diffraction-limited" (0.80 Strehl) field radius to 4.8 arc minutes (81mm).

Due to testing errors, HST was sent to space with incorrectly figured primary mirror: it was a hyperboloid 2200 nanometers shallower than what it was supposed to be (in terms of mirror conic, -1.0137 instead of -1.0023). The four-wave surface error translates into twice larger error at the paraxial focus, but at the best focus location it diminishes fourfold, to "only" two waves P-V wavefront error of spherical aberration (picture below; note different scales for the flawed and design ray plot spots). While not making the telescope useless - even in 0.5 arc second seeing the seeing-induced long exposure error would have been larger - but it was taking away most of the atmosphere-free environment advantage. Lackily, the error was correctable: all it took was a pair of small, coin-size mirrors placed close to the focal plane of each of the instruments (the first is a plain tilted sphere, reflecting light to the actual corrective mirror with appropriate aspheric, as well as apropriate shape to correct for tilt-induced astigmatism, reflecting light back toward instrument).

While the secondary size needed to fully illuminate the field is only 1/8 of the aperture diameter (D), the effective central obstruction is around 0.31D, needed for proper baffling. MTF graphs show the effect of field astigmatism (left) and figuring error (right) for the base wavelength.

10 - 1.24m f/2.5 U.K. Schmidt Telescope (UKST)

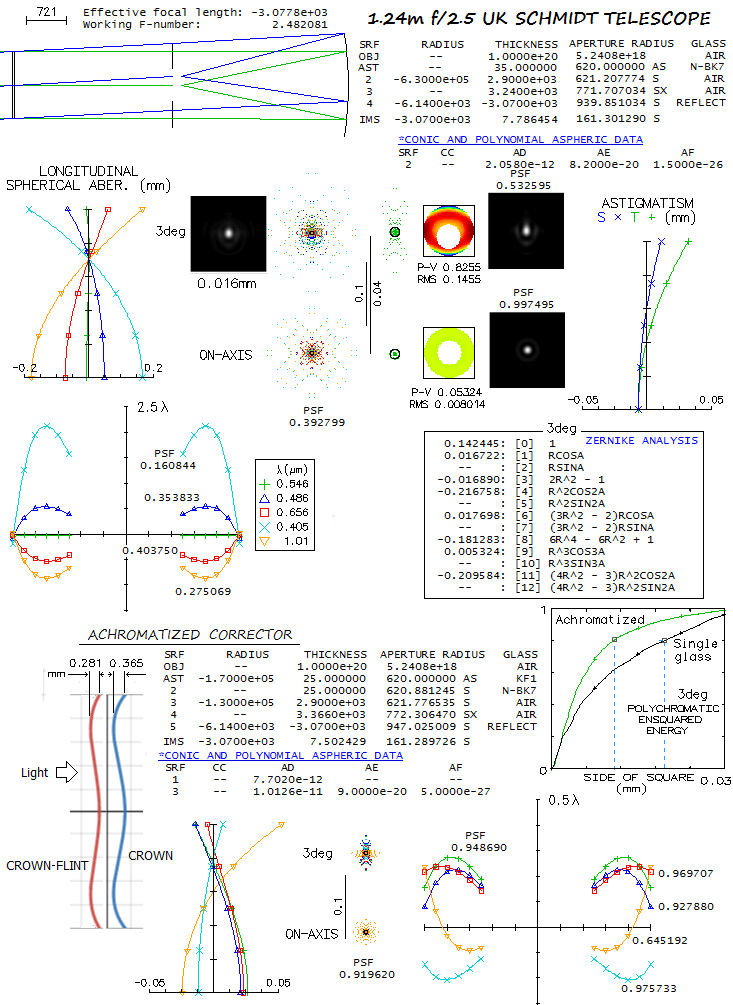
This headline is a bit misleading, because this instrument is not in the U.K. - it's at the Siding Spring Observatory, New South Wales, Australia - nor it is a telescope. While meter-classs professional telescopes are never used for visual observations, they do have accessible image and could, technically, use eyepieces. The UKST, as all Schmidt "telescopes", can't - it is a camera. It is a younger cousin to the Oschin Schmidt "telescope" at the Palomar Observatory, U.S. They are nearly identical in all respects, except that the Oschin Schmidt started out (1948) with a single-glass corrector, replaced with achromatized one in the mid-80s, and its original photographic plate detector was replaced with CCD. On the other hand, UKST had achromatized Schmidt corrector from the get go in 1973. and kept ist photographic plate detectors; from the 2001th on, it was used mainly for multi-object spectroscopy and radial velocity measurements.

The UKST covers field of 6.5x6.5 degrees, which requires 1.9m mirror for zero vignetting (the actual mirror is 1.83m in diameter). Below is what its performance looks like in raytracing, for the single-glass corrector (top) and achromatized one. I didn't find what glass combination was used for the latter, and relied on the achromatic Schmidt coverage in Schroeder's "Astronomical Optics". Given is the one that worked the best, even if KF1 (Schott) is obsolete now, because the corrector is not fully optimized, and the other possible combinations - for instance BALF4/BK7 or NSL36/BSL7 - are close behind. Also, based on the size of the field, central obstruction is approximated at 0.6m in diameter; the actual one shouldn't be significantly different.

At 3° off axis, Zernike analysis for the single-glass system (top) shows only three significant aberrations: primary astigmatism (4), primary spherical aberration (8) and secondary astigmatism (11). However, the first two are not the actual aberrations. This configuration is free of primary aberrations, except field curvature. The "primary astigmatism" is actually a secondary aberration that has identical form, but increases with the 4th power of the field height (lateral astigmatism). Likewise, the "primary spherical" is a secondary aberration, identical in form, that increases with the square of field height (lateral spherical). Obviously, if we have less than 0.01 wave RMS of primary spherical on axis, we can't have 0.081 wave RMS of it at 3° off (as determined by the Zernike term value, 0.181, divided for primary spherical by 5^0.5).

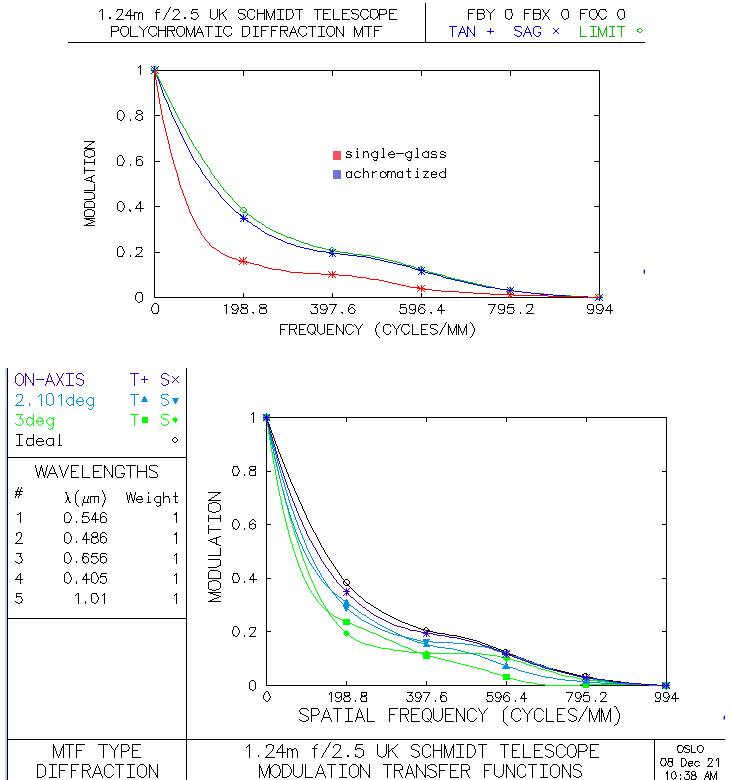
Achromitezed corrector (bottom) significantly improves performance level. Polychromatic Strehl jumps from 0.39 to 0.92 (400-1000nm, even sensitivity), and the square with 80% energy at 3° off axis drops from 0.02mm to 0.011mm (0.74 arcsec; 0.5 and 1.3 arcsec on axis, for the achromatized and single-glass, respectively). This directly determines both, limiting resolution and contrast transfer efficiency. However, achromatized corrector requires significantly deeper curves: 0.281mm and 0.365mm vs. 0.076mm for the single-glass curve (all three have point of inversion, i.e. maximum deviation at ~0.71 zone).

Of course, these figures are valid only for zero atmospheric error, tube currents and misalignment. The first factor is the most significant: even in 1 arcsec seeing, this aperture is subjected to a D/r₀~9 turbulence, with its diffraction pattern broken into a speckle structure, bloated into a blur several times the Airy disc size. In order to have its atmosphere-free PSF maxima still intact, the camera would need 0.2 arcsec, or better seeing. 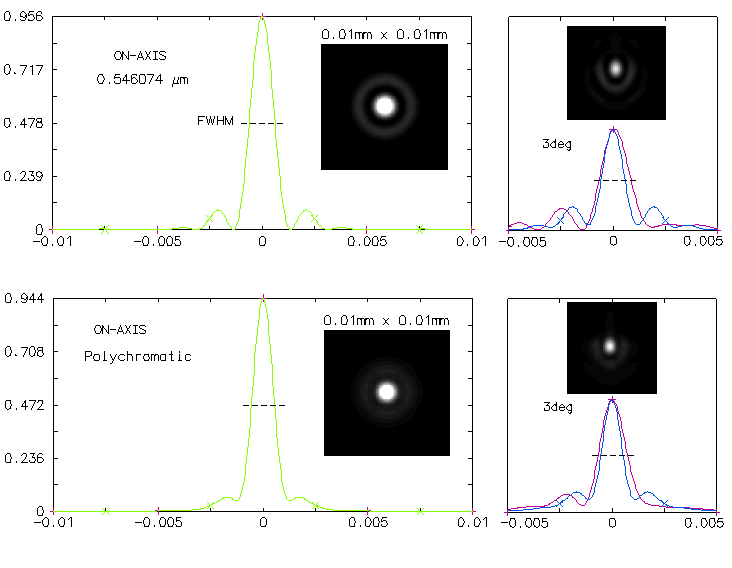Image below shows the system PSF for achromatized corrector; due to the 0.48D central obstruction, the central maxima diameter is about 20% reduced, and the FWHM for the e-line little more than 7%, at less than 0.0013mm, or below 0.09 arc second (PSF simulations are in different proportions to the graphs, and among themselves for center vs. off axis).

In 1 arcsec seeing, the FWHM would be enlarged to roughly 0.5 arcsec - little better than FWHM of the 8-inch aperture. PSF simulations are normalized to 0.5 intensity, thus the bright central disc approximates the FWHM. The polychromatic FWHM is smaller than the e-line FWHM due to wave interference; neither changes appreciably in size at 3° off axis, although some elongation - mainly due to lateral astigmatism - is noticeable. Either FWHM encircles less than 50% of the energy. Atmospheric enlargement of the FWHM would significantly lower the sytem's design contrast transfer efficiency, shown below.

The MTF shows that the effect of obstruction - determining the contrast transfer limit (green plot) - is much more of a factor than system aberrations with achromatized corrector (top). Transfer efficiency decreases toward outer field, but remains effective, except for the cutoff frequency reduction in tangential plane, due to the aforementioned FWHM elongation (bottom, for achromatized corrector).

11 - The Vatican Advanced Technology Telescope (VATT)

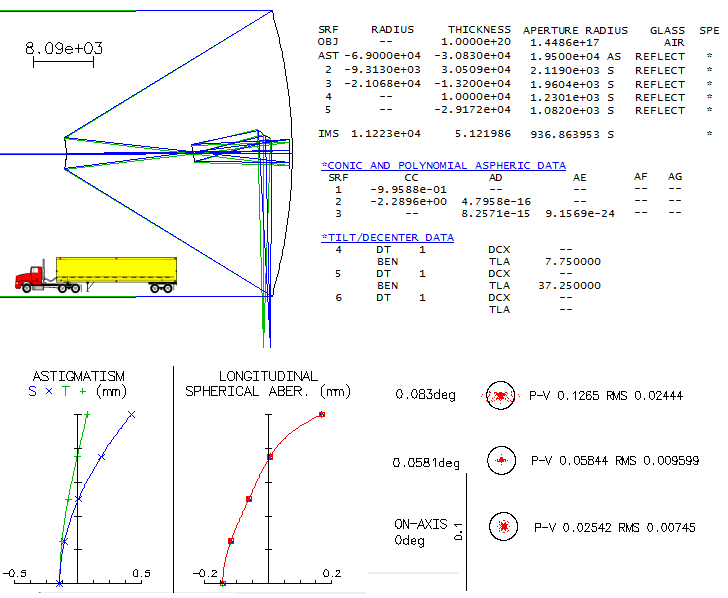
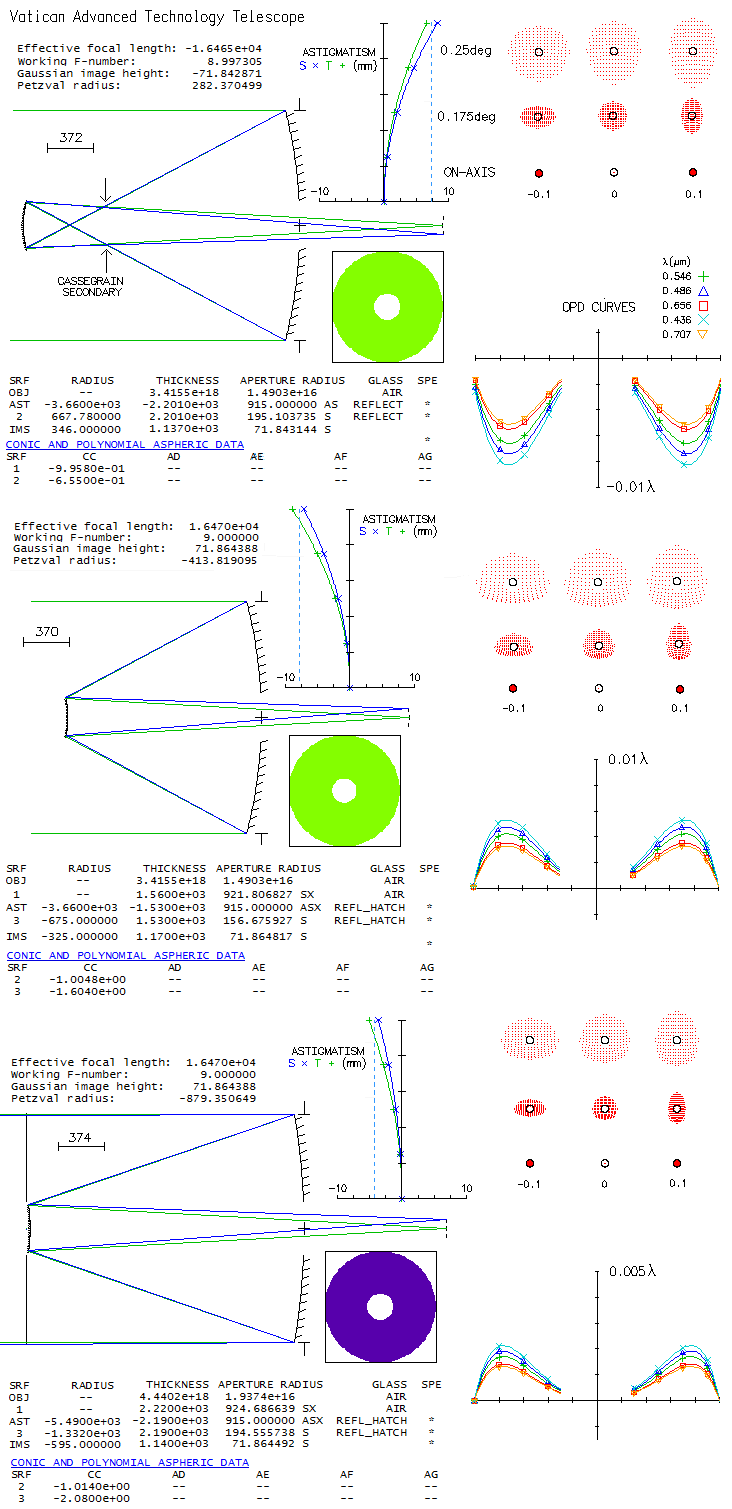
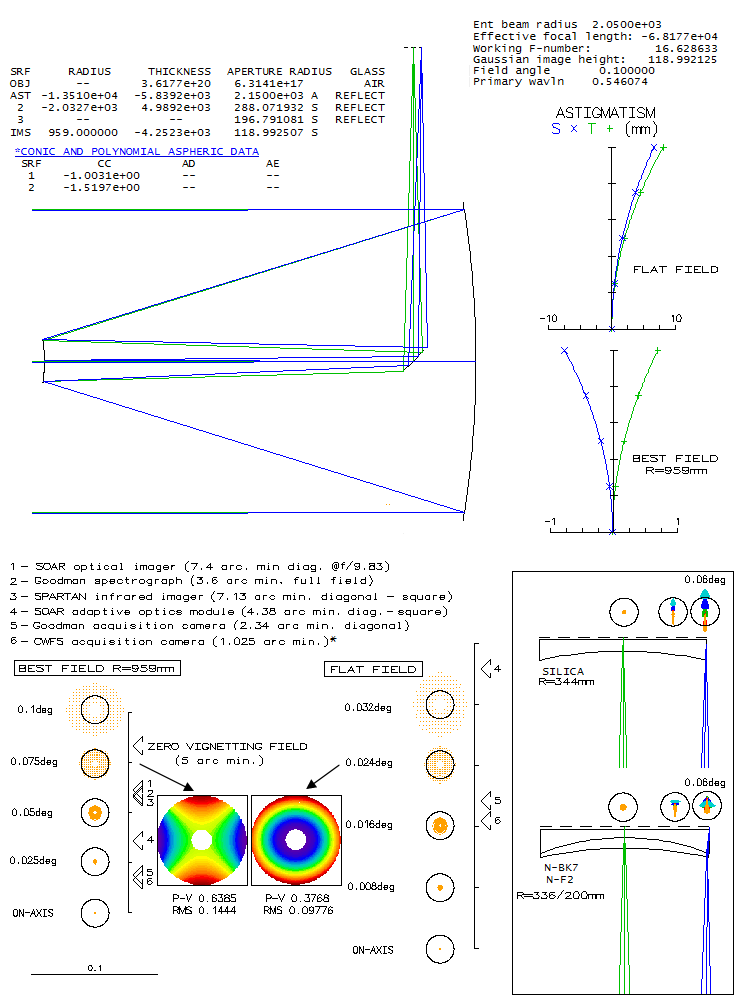
A part of the Mount Graham International Observatory, Arizona, this 1.83m with f/1 primary is rare exception in that it employs aplanatic Gregorian two-mirror system, instead of the usual aplanatic Cassegrain, also known as Ritchey-Chretien. Is there something in the optical properties of its image that makes it the favorable choice, since the compactness obviously is not its advantage? Here's what raytrace shows.

Compared with aplanatic Cassegrain with the primary of the same focal ratio, and with nearly identical focal length (middle), the Gregorian has slightly less curved best image surface, and slightly less astigmatism. The Cassegrain, on the other hand, has slightly smaller central obstruction (0.4m vs. 0.43m, as the secondary diameter needed to fully cover 0.25° field radius, enlarged 10% as the minimum needed for the secondary housing), and 18° shorter secondary-to-final-image separation.

But comparing the VATT with a Cassegrain of nearly identical secondary-to-final-image separation seems more appropriate. In that case, the Cassegrain sports an f/1.5 primary, significantly more relaxed field curvature, nearly 20% lower astigmatism and identical central obstruction (bottom). Hence, the Cassegrain offers better overall performance level, although the difference is still small.

Interesting detail is that all-reflecting systems do have non-zero chromatism (other than that caused by different diffraction pattern size at different wavelengths). In presence of spherical aberration, the magnitude of aberration is inversely proportional to the wavelength.

12 - James Webb Space Telescope

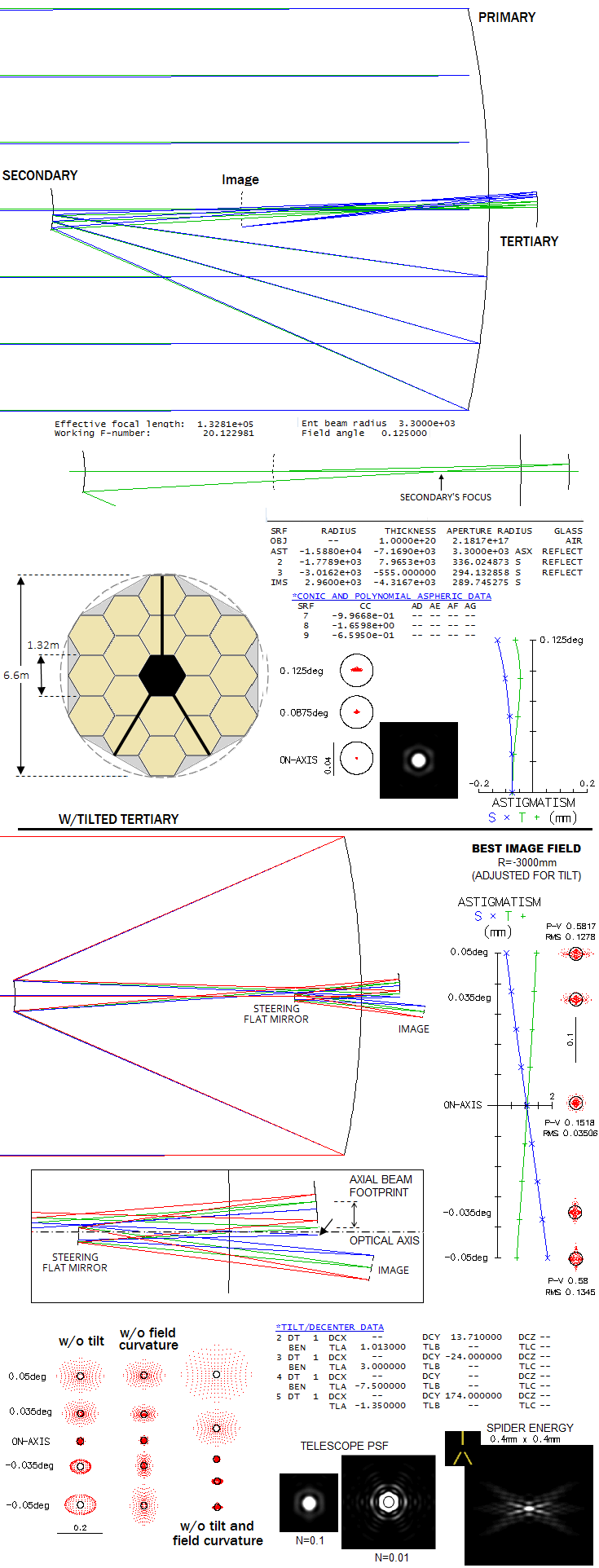
JWST came as a replacement for the Hubble Space Telescope. It is a 6.6m f/20.1 three-mirror Korsch anastigmatic aplanat. The primary is made of 18 hexagonal mirrors forming near-paraboloidal f/1.2 ellipsoidal surface (gray area around it fills in to the simplified shape used for the raytrace). The secondary is a hyperboloid, and tertiary prolate ellipsoid. In order to make it more practical for use with instrumenation chamber, the tertiary is tilted to reflect converging light onto the flat steering mirror placing the final image behind the primary. It will operate in a wide infrared spectrum (0.6-27 micron), with one of primary purposes being collecting information about first light sources in our Universe, within the first galaxies, red-shifted to near-infrared and centered around 2 micron wavelength, at which it should be "diffraction limited" (0.80 Strehl). Apparently, JWST already discovered what should be the oldest known galaxy - GLASS-z13 in Ursa Major - 13.4 billion years old (at the time it formed, it was 3 billion light years from where we are now; light traveled 13.4 billion years to reach us, but the distance between us today is, due to expanding Universe, over 33 billion years). At the time it formed, Sun didn't exist, and the galaxy probably doesn't exist now.

Image below shows the optical system, performance of the basic design (top) and the actual design with tilted tertiary and added flat mirror (bottom). Design data is from "James Webb Space Telescope: large deployable cryogenic telescope in space", P.A. Lightsay et al. (prescription given there does not contain tilt and decenter data, so the design is in that respect approximation). Field angle shown with the basic design is somewhat larger than in the actual telescope (up to 0.1 degree radius, judging on the size of tertiary mirror on a system drawing) in order to make ray paths discernible. Design correction is excellent over the best image radius (2600mm, concave toward secondary). Over flat field though, the edge spot bloats to 3/4 of a milimeter.

Tilting the tertiary induces strong astigmatism, much less of coma, as well as image tilt. Here, field radius is 0.05° (3 arc minutes), which is probably closer to the actual telescope (also, it is about the maximum for the 3° tertiary tilt). After adjusting for image tilt and curvature, correction level is excelent, from better than 1/8 wave P-V equivalent of lower order spherical aberration on axis, to a little over 1/2 wave at 1/20 degree off (minimizing spherical aberration requires slightly lower primary conic, -0.9967). The field could be still slightly corrected for tilt, but it wouldn't produce appreciable gains. Best image surface radius is now -3000mm, concave toward flat mirror. The only point image aberration is low-magnitude primary astigmatism. Ray spot plots bottom left show what the field looks like without corrections for tilt and field curvature. There are big discrepancies between decenter stated in the article (0.19mm for the tertiary) and workable values. If the tertiary is tilted, it induces very strong astigmatism and coma; astigmatism can only be offset by tilting the secondary (which is evident on both published drawings and raytrace presentations), while decentering it induces coma. To have it all balanced requires also decentering the tertiary, which also induces coma, but primarily astigmatism. One peculiarity is that tertiary can't be centered around axial cone; it is shifted up with respect to it (small arow shows bottom of the blue diverging cone at the tertiary). In effect, light falling onto it is using an off-axis section of that ellipsoid. When the tertiary is positioned axially, minimizing astigmatism requires decreasing its tilt angle, and that cannot be done since it is necessary for placing the flat out of the light cone.

Note that the Airy disc shown is for 0.5876 micron wavelength, just below the lower end of the telescope's operational spectrum. Airy disc size changes in proportion to wavelength, so at the 2 micron wavelength it is 3.4 times larger - with the aberration proportionally smaller - and at 27 micron as much as 46 times larger. With the effective focal length of nearly 133m, one arc second spans 0.64mm. Resolving power of the aperture (neglecting central obstruction effect), λ/D ranges from 0.0188 arc seconds at 0.6 micron wavelength (0.0006/6600 times 57.3x60x60, to convert from radians to arc seconds), to 0.84 arc seconds at λ=27 micron. This implies that quality field varies significantly with the wavelength.

Simulated PSF (bottom right) show that the axial diffraction pattern, due to near-hexagonal shape of the primary, has also hexagonal 1st bright ring; central maxima appears slightly non-circular, but larger images show it perfectly round. With intensity normalized to 0.01 - note that scale for these two patterns is different - the pattern shows low-energy regions forming hexagonal wide-spike pattern (intensity points equal and higher than 0.01, or 1% of the central intensity are white). Energy spread by the spider vanes, shown as an inverse aperture, has most of the concentration in the central maxima, roughly 1/30 mm long, two pairs of V-shaped spikes and two elliptical spots above and below the maxima. The approximate width of the vanes is 6 inches. Central obstruction, determined by the missing central segment, is approximately 20% by diameter (23% when extracted from the area).

As already mentioned, this design is approximation, since no complete prescription was available. In the final optimization astigmatism can be even further reduced, but the correction is already very satisfactory. Axial correction error could be further reduced by making the primary figure accurate to yet smaller decimals, but it is neither necessary nor realistic (at the optimum primary conic, -0.996754, coupled with -1.66 secondary conic to keep the coma minimized, axial correction is 1/74 wave P-V of mainly primary astigmatism and some secondary coma, with the error at 0.05° off axis reduced by less than 10%). This design shows that the design limit for JWST is significantly better than 0.80 Strehl in 2 micron wavelength, on and off axis. But fabrication is always less than perfect, and collimation, pointing and thermal errors cannot be entirely eliminated. 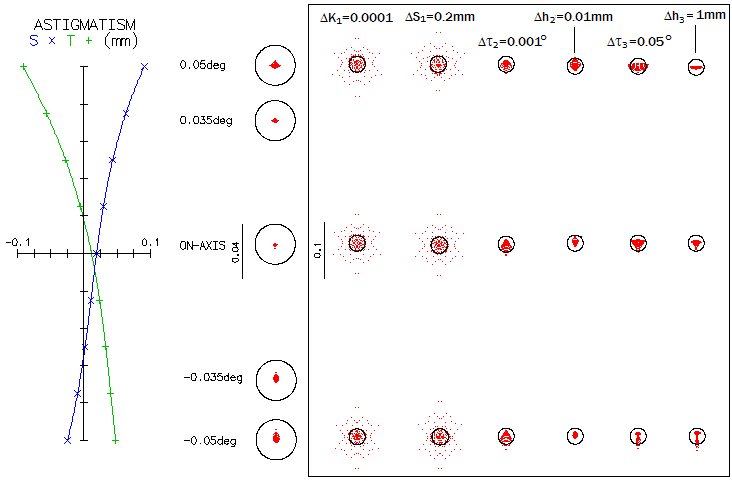Below is illustration of the sensitivity of this system to some of the basic possible errors. For clarity, aberrations at the system limit are further reduced (left). It is achieved by tilting the tertiary somewhat more, to 3.15°, with slight changes in the decenter of the secondary (13.705mm) and tertiary (-19.7mm; putting -19.69mm brings zero astigmatism point to the field center, but has no practical significance); optimal primary conic is -0.996755, and -1.66 on the secondary.

Inside the box, effect of very small changes in the figure (primary) and position of the mirrors on the ray spot plots (note that the scale is 2.5 times larger in the box; Airy disc is, as before, for 588nm wavelength). From left, change in the primary conic, primary-to-secondary separation, secondary tilt and decenter, and tertiary tilt and decenter (all changes are smaller in their absolute value than the optimum). In general, induced aberrations change in proportion to the deviation: doubling the deviation doubles the (induced) aberration. As little as 0.0001 deviation in the primary conic - and that is an f/1.2 18-segment surface - induces 0.075 wave RMS (slightly below 0.80 Strehl) of primary spherical aberration in the 588nm wavelength; at 2 microns, it will be smaller in inverse proportion to the wavelength, i.e. 0.022 wave RMS. The sensitivity to the secondary tilt is not a typo: as little as 1/1000 of a degree induces about 0.045 wave RMS (@588nm) of all-field coma.

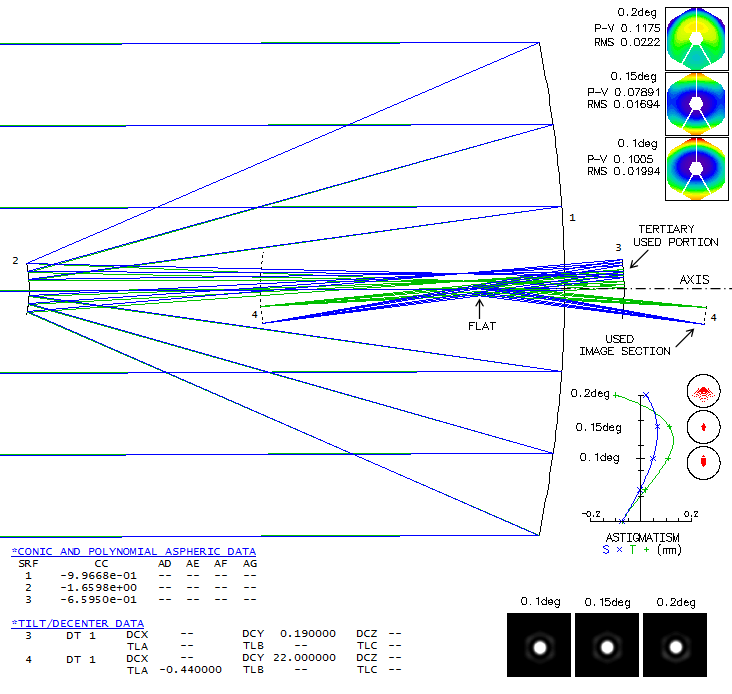
ACTUAL DESIGN - After I've put here on what appeared to be approximation of the JWST optical design, I had a whisper to my ear (Mike Jones) telling me what the actual design should look like. I'll keep the above system here as a tilted-mirror alternative, but the actual design keeps them orthogonal to the axis. Except above mentioned slight tertiary decenter - purpose of which is to tilt the image so that the used portion becomes nearly perpendicular to the optical axis - there is no other perturbations in the mirrors' rotational symetry vs. optical axis. As image below shows, the flat is centered around optical axis, but it is not in the light path because JWST uses only off-axis section of the image field (that's why it appears that both secondary and tertiary are tilted). In this case, the green cone forms image point at 0.1° off axis, and the blue cone point at 0.2°. Usable image is between 0.1 and 0.2 degree off axis.

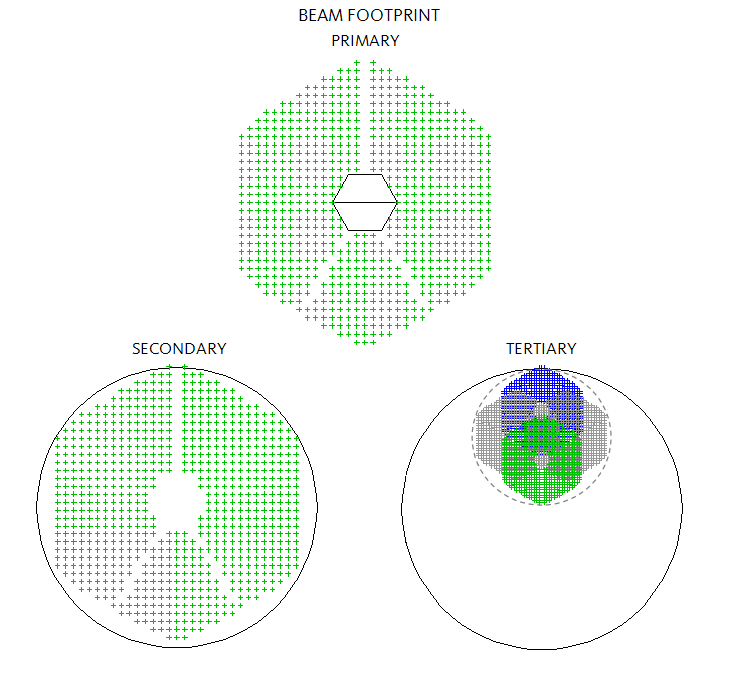
Due to this geometry, light forming the image uses only part of the upper half of the tertiary, with the rest being removed to allow light reflected from the flat to form image beyond the tertiary. Beam footprint for the 0.1° field point at the primary (aperture stop, 1), secondary (2) and tertiary (3) is shown below. Since aperture stop is on the primary, any field angle has identical footprint on it. It is differs only slightly on the secondary, while on the tertiary all footprints fit on the upper half of it (for 0.1° field radius on the primary and secondary, for both on the tertiary; needed tertiary radius for zero vignetting is 398mm, and 345mm for the secondary). The dashed circle is the off-axis section on the tertiary containing all beams for a circular field.

Tilt and decenter of the image are only to show its characteristics over the used portion, when positioned optimally vs. cameras. Correction - as the design limit - is still exsquisite (note that this is the same astigmatic field shown above with the basic design, only expanded to 0.2° radius; in the outer field, higher-order astigmatism kicks in causing tangential surface to cross over the sagittal). The field could be extended outward by manipulating astigmatism, without significant effect on the correction level, but the limit to its size is set by the need to keep it nearly flat. In this case, the diameter is 0.1°, or six arc minutes. The field could also be extended toward axial cone, but no more than one arc minut, or so (w/o vignetting).

13 - EXTREMELY ACHROMATIC 19-INCH f/1* CAMERA

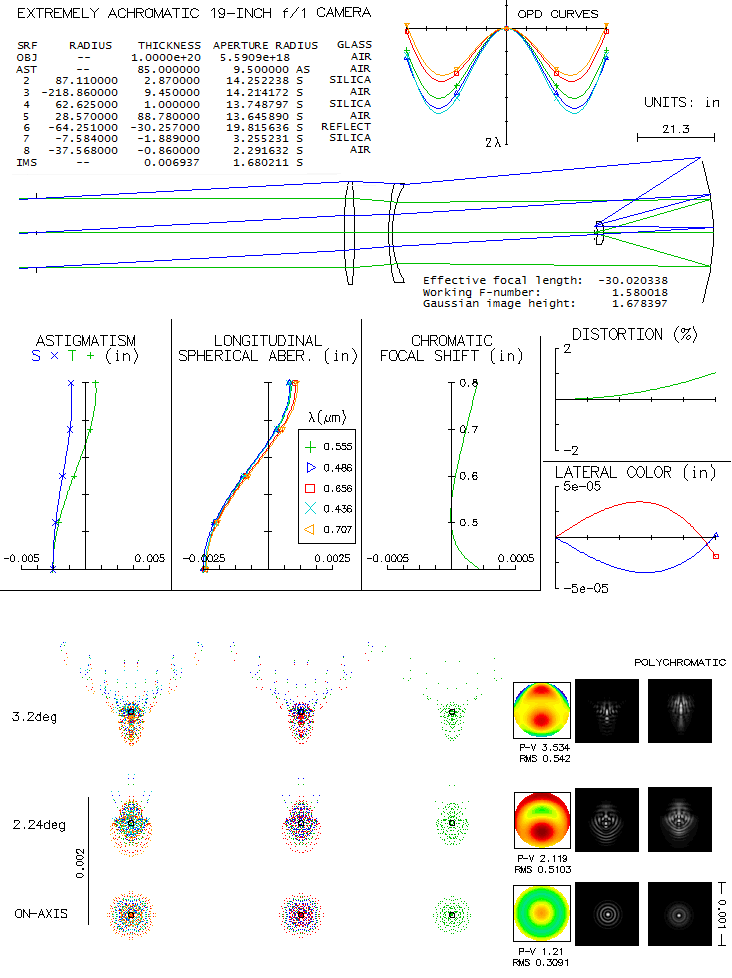
"Extremely achromatic" is how Epps and Vogt described the camera they designed for the Keck telescope spectrometer in 1993 (Extremely achromatic f/1 all-spherical camera constructed for the high-resolution echelle spectrometer of the Keck telescope; drawing by Epps with the prescription data published online is from 1990). It is probably as simple as such a camera can be: all-spherical, consisting of a two-singlet full aperture corrector, mirror, and a single field lens made of the same glass as the front end corrector. Unlike the old-fashioned Schmidt/Houghton cameras, it comes with flat field (a comparison could be interesting). Below is how it raytraces with OSLO Edu. As both, LA and OPD plots show, there is no longitudinal chromatism to speak of, although the colors could be made yet little tighter (camera was intended for 0.3-1.1 micron range - and beyond - but here it is raytraced only for the conventional visual 0.43-0.67 micron range; obviously, there is enough room to go toward longer wavelengths, since the red end here is beter corrected than the central line).

The spherical aberration leftover on axis could be minimized to better than "diffraction limited" (0.80 Strehl), but may have been left in on purpose, in order to make the point image energy spread over the field more even. Field seems to be limited to less than 4° radius by departure from flatness and higher order aberrations (in the sense that star images remain similar in size). At 4°, trefoil becomes the dominant aberration form, and quadrafoil becomes the third, after primary astigmatism (which probably includes significant portion of Schwarzschild's lateral astigmatism). Paper cites 1.8 inch (3.4°) field radius, but here it is 3.2°, which gives more even field quality. Diffraction simulations show fairly even blurring accross the field, with the dense blur portion well within 0.001 inch (0.0254mm). 80% energy radius is 0.0072mm at the 70% radius, and 0.0089mm at 4 degrees (2 and 2.4 arc seconds, respectively).

There is a discrepancy between the claimed f/1 focal ratio, and the actual f/1.58. Aperture stop radius on the drawing is given as 9.5 inch, and the focal length given in the abstract is 30 inch; that produces f/1.58, not f/1. With a bit larger field, the front lens radius needed to accept all incoming light goes to 15 inches, but it is not the aperture stop, and the focal ratio remains f/1.58. Pulling the stop all the way back to the font lens changes little in the magnitude of aberrations. If the stop at this location would increase to 15 inch in radius, it would produce a f/1 system - but it would be a different configuration, with significantly inferior performance (although better than with the stop expanded to a 15-inch radius at its original location).

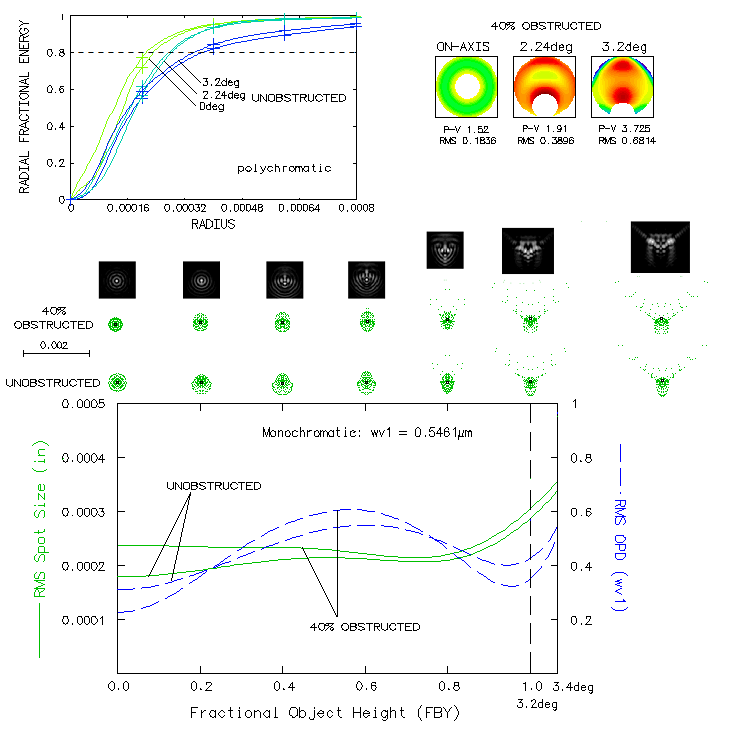
Below are ploted encircled energy (top) and RMS spot size/OPD for the field (bottom). So far, central obstruction effect was omitted, but it obviously cannot be avoided, and has to be relatively significant. For 3.2° field, minimum central obstruction size, determined by the size of field lens (for full field illumination) is about 40% linear (image itself is about half as large). Encircled energy plots for the five wavelengths, even sensitivity, (top left) indicate that obstructed aperture has smaller 80% encircled energy radius up to 70% of the field radius, but keep in mind that the starting point, i.e. unit energy in the obstructed aperture is over 10% smaller PSF (linearly), whose central maxima contains less than 71% of the energy of the unobstructed central maxima (the unmarked plots are for unobstructed aperture, with identical color code field-height wise).

Ray spot plots for obstructed and unobstructed aperture are generally similar. Diffraction simulations (for the actual, obstructed aperture) are about twice larger, for clarity. Patterns are similar to those of unobstructed aperture over most of the field, but closer to the edge they spread wider. The RMS spot size (radius) is generally smaller for unobstructed aperture, even on axis, due to the smaller obstructed spot here being of even density, while the unobstructed spot has two denser inner areas (most dense around the center), not clearly discernible at this scale. The RMS spot size (given as radius) is nearly constant up to 90% of field radius, after which quickly increases, mainly due to trefoil-like deformation. Over about 80% of field radius the RMS spot is little over 0.0002" (0.005mm, e-line) vs. 0.0126mm (diameter) cited in the paper as the whole (3.4°) field average, making it suitable for 7-15 micron pixel chips. Diffraction images above match this averaged RMS spot size fairly well.

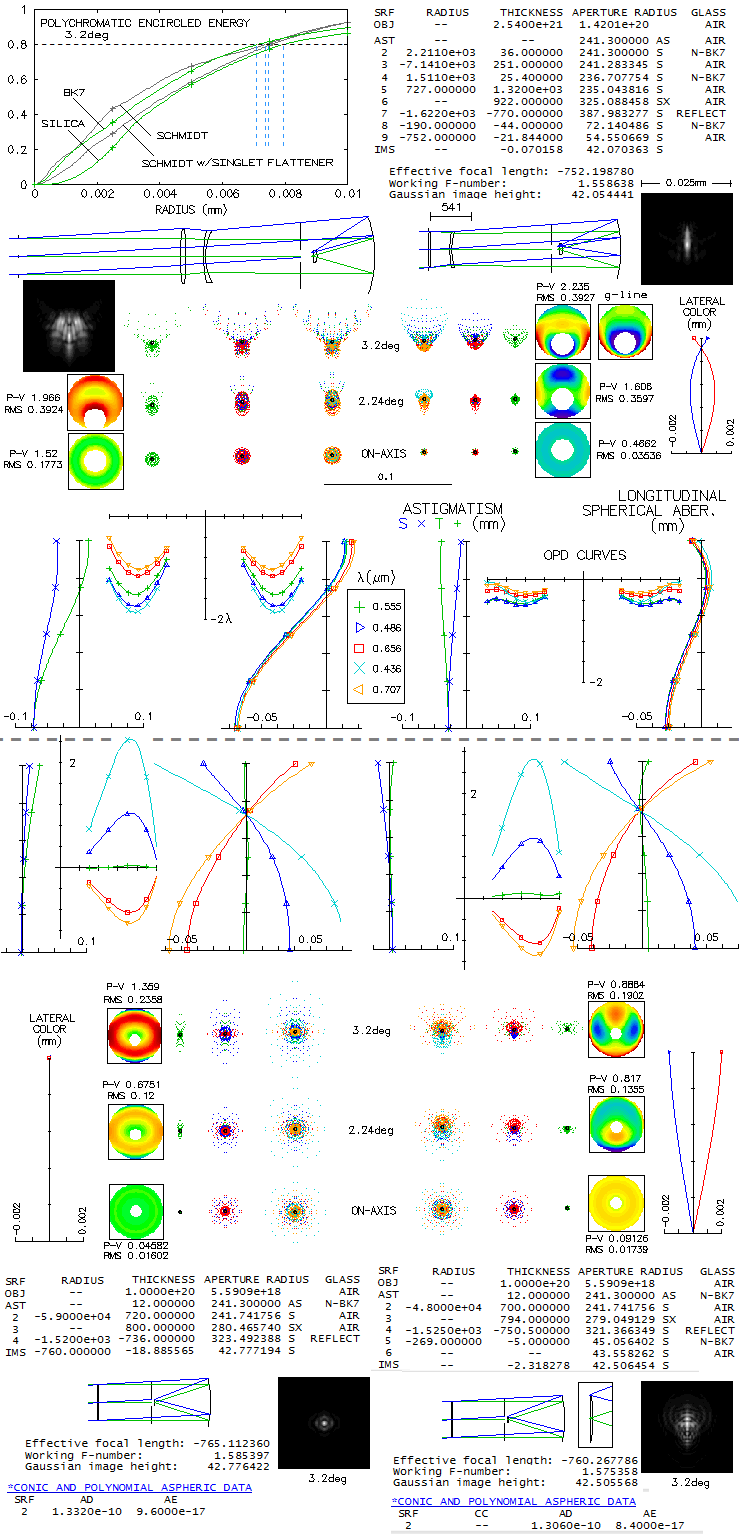
This optical arrangement is simple enough to be within reach of the advanced ATM. Scaling it down to, say, 6 inch aperture, would have the blur size reduced by a factor of 0.4, to some 4-5 microns. Below is described system of this kind, using BK7 glass and with the stop at the fron lens, suitable to be used as a stand-alone camera. Still, at this fast focal ratio tolerances are very tight. For instance, just 1mm shorter front field lens radius would negatively affect lateral color correction. As mentioned before, significantly reducing stop separation, even placing it at the front lens, would have relatively minor consequences. As mentioned, minimum central obstruction, due to the assembly that would house the field lens and detector is about 40% linearly at this field size (image itself is always significantly smaller).

To have better idea of the degree of chromatic and overall correction of this arrangement, we'll compare to a known standard, the Schmidt camera of the same aperture and focal ratio. Linear central obstruction is 40% in the Ebbs-Vogt systems, and 20% Schmidts. In addition to the above system (top left), standard Schmidt (bottom left) and flat-field Schmidt (bottom right), included is the above system with silica replaced with the Schott BK7, with the stop at the front lens (stand-alone camera, top right). It compares favorably to the system with a distant stop both, size wise, and with respect to overall correction. In order to make chromatic correction easier to compare, both Schmidt systems and the "short" Epps-Vogt have minimized error on axis; that influences somewhat field correction. System drawings are nearly on the same scale, thus directly comparable size-wise (note that the Schmidts and "short" Epps-Vogt prescrptions are in mm).

The two Epps-Vogt systems have very similar level of chromatic correction, but the "short" version is easier to compare to the Schmidts. Its superiority in the axial chromatic correction is obvious immediately, in all four non-optimized wavelengths (note that the nominal P-V error is not representative in obstructed systems, since measured from the non-existing vertex, while the RMS is measured only over the annulus area). Better overall axial color correction for 0.3-1.1 micron range would have the blue/violet focusing longer - as in the original design, or even more - because yet shorter wavelengths focus shorter, and the error on the violet end is much larger than on the infra-red.

Epps-Vogt systems have about half the lateral color of the flat-field Schmidt, while that of the standard Schmidt is practically non-exsistent on the given scale. Polychromatic encircled energy (top left), however, shows that there is not so much difference in the 80% encircled energy radius (the five wavelengths, even sensitivity). Better chromatic correction of the Epps-Vogt is mainly offset by the better field correction of the Schmidt. Diffraction simulations for 3.2° field radius (polychromatic, the five wavelengths, even sensitivity) show significantly more difference in the intensity distribution pattern, than in encircled energy. Note that placing stop at the front surface produces similar type of field edge pattern in the original Epps-Vogt; for some reason, they opted for somewhat wider, but more evenly mixed color-wise spread toward field edge, even at the price of a widely separated stop (some stop separation is inevitable with spectrographs since the camera has to be preceded by the collimator and dispersive element). The coma-like ray spot plot is actually produced by a wavefront deformation closer to astigmatism; as the wavefront maps show, it affects a narrow outside wavefront side strips, mainly on the bottom half, with the edge wrinkle spreading to the bottom, and becoming nominally larger toward shorter wavelengths. The relative area of deformation is quite small, and so is the amount of energy spread out.

14 - The 500mm f/9 Solar Optical Telescope

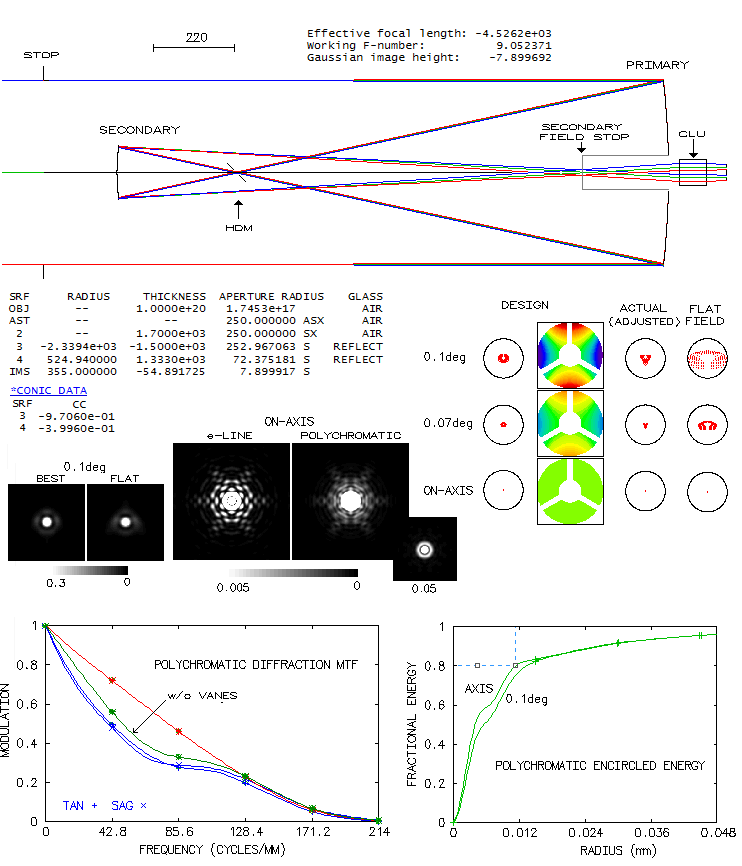
Described as "the largest state-of-the-art solar telescope (...) ever completed and flown in space" (The Solar Optical Telescope of Solar-B (Hinode): The Optical Telescope Assembly, Suematsu et al. 2008), it was designed for high-precision photometric and polarimetric observations of the Sun in the visible spectrum (388-668nm). Placed out of the atmosphere - Solar-B satellite, later renamed to Hinode - it is capable of resolving magnetized structures down to 0.2 arc seconds, out of reach of ground based telescopes. This requirement was the main factor determining the aperture size. The system can be separated into two components: (1) Optical Telescope Assembly, consisting of a two-mirror Gregorian, collimating lens unit (CLU), polarization modulator, tip-tilt mirror and astigmatism-correcting lens, added to correct axial astigmatism generated at the primary most likely due to a mounting stress, and (2) Focal Plane Package with CCD detector, where the final image is formed. The collimating lens unit, consisting of six singlets, is in effect a double apochromat, each having opposite sign of low-temperature sensitivity. The tip-tilt mirror stabilizes image and folds collimated beam to the side, toward Focal Plane Package, where it passes through re-imaging lens unit before falling onto a 4000x2000 pixel detector.

The two-mirror optical system is aplanatic Gregorian, with 0.344D central obstruction by the secondary. Secondary is supported on a 120° 3-vane spider, with 40mm wide vanes. Entrance aperture is 200mm ahead of secondary's surface, i.e. 1700mm from the primary. Small diagonal mirror placed at the prime focus is a heat dump mirror (HDM, with an opening about twice the diameter of the solar image). At the final focus, there is a secondary field stop - 361.3x197.4 arc seconds rectangular hole (about 6x3.3 arc minutes, or 8x4.4mm) in a conical mirror of 65mm outer diameter. It determines the usable field.

Gregorian offers the advantage of having two field stops between the primary and secondary mirror. Also, in a similar configuration with f/9 focal ratio, a Cassegrain would require a small, strongly curved secondary, resulting in a twice larger wavefront error at 0.1° on flat field. Ray spot plots on the left are for a perfectly executed design. With a very minor fabrication imperfections in the mirror conics and radii, the error - mainly spherical aberration - exceeds 1/4 wave P-V, but it is practically entirely cancelled increasing the mirror separation by 1.6mm (right). At 0.1° flat field error is still less than "diffraction limited" (0.80 Strehl). Error budget for the system is 0.80 Strehl (36.5nm RMS WFE), or better, with 0.9 Strehl limit (25.8nm RMS) alocated to the optical tube, and as much for the focal plane package. Actual measurements came out better, at the level of 12nm on individual mirrors (about 17nm combined, for the 0.034 wave RMS WFE at 500nm wavelength). The mirrors use protected silver coating with 96% reflectivity and 6.5% solar absorbance.

The vanes are fairly massive, but the good side is that it creates short spikes. Still, MTF shows that they do significantly lower contrast transfer over the entire range of frequencies (there is also relatively small dependance of the contrast transfer on image orientation). They are more pronounced in polychromatic light, along with a loss of inner structure of the diffraction image (peak normalized to 0.005 means that every point with a higher intenity shows white). Polychromatic encircled energy (even sensitivity 430-670nm) gives 80% radius of 12 microns (on axis), wich at this image scale corresponds to 0.56 arc seconds. This is mainly due to loss of energy to the first bright ring, caused by the central obstruction and vanes. Resolution limit for high-contrast details is determined by the size of the central diffraction disk, nearly three times smaller.

15 - 3.6m f/200 AEOS telescope

The U.S. Air Force Advanced Electro-Optical System (AEOS) telescope, located on the Hawaiian volcano Haleakala, uses 3.67m (3.63m clear diameter) f/1.5 primary and two interchangeable secondaries: one with effective diameter less than 5% of the primary diameter, for f/200 and 62"x62" (0.016°x0.016°) field of view, and the other about three times larger, for 202"x202" field of view (in either case about 8x8 inches image area). Primary's shape is controlled with 132 actuators, and the adaptive optics system incorporates CCD wavefront sensor coupled with a 2mm-thick 288mm diameter deformable mirror with 941 actuators. While constructed for space surveillance - primarily satellite tracking - the telescope is also used for astronomical purposes. It operates in spectral range from 540nm into infrared.

System below is a raytrace of similar configuration. Since no prescription is given, it is only a close approximation of the actual system. It is assumed the system is Classical Cassegrain, since there is no benefit from making it aplanatic. The length of converging beam from the secondary is over 30m, with a series of flat mirrors bending it through a couder path around the primary (through the altitue axis, and than through the azimuth axis) to the basement where are located instruments.

Shown is a system with the smaller secondary (the actual secondary is probably a bit smaller, with correspondingly shorter back focal length). Despite the fairly strong field curvature, due to the very small field of view there is no appreciable effect on off-axis performance. Ray spot plots top left are the actual shapes over best field, too small to be recognized within the Airy disc. With the larger secondary and three times larger field, off axis performance is similar over the best field, but over flat field the field edge at 0.024° has 0.32 waves P-V (0.09 waves RMS) of defocus - about three times more than with the f/200 secondary (approx. three times weaker field curvature results in about 1/3 as much of linear defocus, but the wavefront error is inversely proportional to the square of focal ratio). Average measured 200ms FWHM with 850nm filter is 0.13 arc seconds (6.5 pixels), which is 2.7 times the theoretical limit (High resolution imaging with AEOS, Patience et al. 2001). Scaled linearly down to 550nm wavelength, it would come to less than 0.09 arc seconds.

16 - 150mm f/15 Zeiss-Coude-refractor

This rather a small aperture refractor for observatory setting was not intended for professional-level use. It was designed by Zeiss as an observatory/educational instrument for public use, i.e. for popularization of astronomy. Its Coude-style mount makes the final image stationary, independent of the movements of optical tube. The mount is very massive, requiring a permanent, observatory-like setup. Both axes are supplied by an electrical motor, and the tube can also be moved manually.

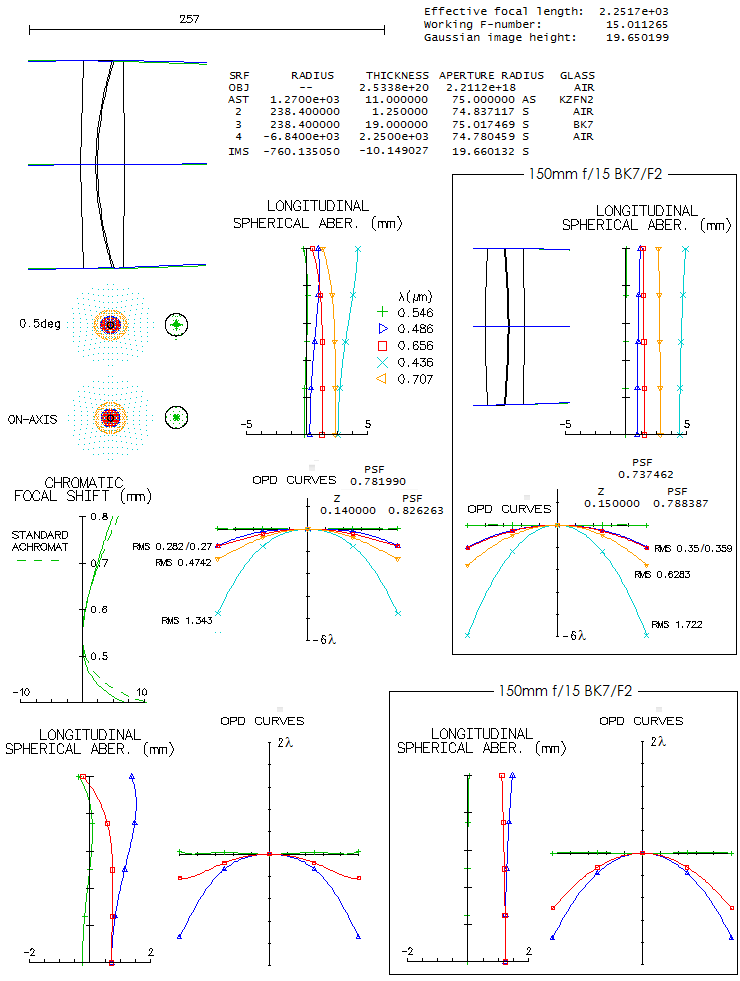
The standard version uses Zeiss AS objective, doublet achromat using Schott KzF2 "short-flint" as the front element and BK7. It is in reverse to the standard achromat, having positive element (crown) in front, and negative (flint) behind. There is no gain in chromatic correction, but the reverse arrangement - known as the Steinheil configuration - requires more strongly curved lens surfaces, thus all else equal produces more of higher-order spherical residual, as well as more spherochromatism. There is no formal eplanation known to me of why Zeiss opted for the Steinheil arrangment for its AS-objective.

The KzF2 seems to be beyond obsolete nowadays, with hard to find refractive properties data, and was raplaced for raytracing purposes with the Schott KzFN2, its more environmentaly friendly, now obsolete near-equivalent.

While it is commonly cited that this objective has significantly - three-fold, or so - reduced chromatism vs. standard achromat, raytracing shows it is much more modest: about 22% in the F and C lines (when nearly balanced defocus-wise), and in the violet g line. Chromatic focal shift graph shows about half as much of defocus between paraxial F and e focus for the AS objective (and no significant difference vs. achromat in the position of paraxial C-line focus), but that is not relevant in the presence of significant spherochromatism. What matters is where the best focus is, which is displaced from paraxial focus due to spherical aberration, generaly stronger in the reverse, Steinheil configuration. Note that this particular objective has correction set for nearly balanced error in F and C; the actual objective could have somewhat different correction mode, closer to the one with the paraxial F and C foci coinciding (i.e. favoring the red end).

Bottom graphs show the imbalance in the F vs. C defocus error when their paraxial foci coincide: it is significantly larger in the Steinheil configuration, favoring the red line correction. When the two lines are balanced, this AS objective has chromatic correction at the level of the f/19.2 standard achromat.

The second flat can be rotated, allowing alternating between the lower and upper focus position. According to Zeiss, standard accessories include five eyepieces (one of them for Sun image projection), one finder eyepiece, one reticle with illuminating device, one pointing eyepiece, one neutral density glass filter, color filters, one ring micrometer, eyepiece spectroscope, and two 2-fold eyepiece revolvers (one for stelar observtions, the other with light-attenuating device for visual and photographic solar observations). On request, the standard AS achromat can be replaced by a 150mm f/15 or f/11 triplet apochromat (F-objective).

17 - 2m Universal Mirror-Telescope

Introduced back in the 1960, this unusual telescope was the largest reflecting telescope in Europe at the time, and still is the largest Schmidt telescope in the world. It is the main telescope of the Tautenburg Observatory near Jena, Germany. Beside Schmidt configuration (f/3), it can also be used in Nasmyth (f/21) and Coude (f/46) configurations, when the corrector is removed, and a Cassegrain secondary placed at 3.44m from the primary. In the Schmidt configuration, its aperture at the corrector is 1.34m, and in the other two it uses the entire 2m mirror. The main 2m f/2 mirror is spherical, made by Carl Zeiss company, originally from low-expansion ZK7 crown, in 1996 replaced by identical mirror made from Sittal. No specifics seem to be given on the size of central obstruction (s), but the minimum dictated by a configuration is 24% linearly in the Schmidt, and 14% in the other two configurations. The actual obstruction is probably larger, particularly in the configurations with secondary mirror, due to baffling requirements. For that reason, central obstruction is omitted in raytracing; its effect shouldn't significantly change the output.

In the Schmidt mode, it originally used 24cmx24cm photographic plates, corresponding to 3.3°x3.3° angular field. Nowadays it uses nearly 1° square CCD with up to 4096x4096 pixels. Either had to be bent to match the best curved field of -4000mm radius. As the astigmatic plot shows, field curvature induced defocus at 2.3° off axis is 3.2mm, which translates to some 80 waves P-V of defocus (2.3° field radius corresponds to the very corner of the photographic plate, with the 0.7 field, or 1.6° is near the plate sides). Even with the much smaller CCD detector, if flat, the curvature-induced defocus would have been 3.9 waves P-V near the side, and twice as much in the corner. Over the best field, the dominant off axis aberrations are oblique spherical and astigmatism, creating a peculiar wavefront shape with roughly flat outer area horizontally, while bent down vertically. The resulting ray spot plot has a shape of wings oriented vertically.

Over the entire photographic plate field, correction is excellent; in the very corner, it is still as low as 1/20 wave RMS in e-line, well within the "diffraction-limited". Spherochromatism is relatively low, the highest in the violet (still, the g-line error is at the level of a 100mm f/65 achromat). Radius encircling 80% of the energy is 0.0027mm on axis, and 0.003mm at 2.3° off. It translates to a circle 0.28 and 0.31 arc seconds in diameter, respectively, for photopic sensitivity (to illustrate correction level in the visual domain), and 0.0043mm/0.0047mm for the average (roughly) CCD sensitivity.

In either configuration with secondary mirror, the imperative is to correct tons of spherical aberration induced by the 2m f/2 spherical mirror. Needed secondary deformation, as well as secondary's radius of curvature for the Nasmyth focus are shown in the box next to it. It requires 8.18 conic (oblate ellipsoid) for the correction of primary spherical aberration (it could be also expressed as a 4th order coefficient, but the conic is more telling), and another three higher order terms, 6th, 8th and 10th, with the yet higher order residual remaining at 0.067 wave RMS. Coma cannot be corrected at the same time, limiting usable field size to a few arc seconds. Although one source states that the usable field is 10-20 arcseconds, raytrace shows that already at 0.001 degree field radius (0.75mm, or 3.6 arc seconds) coma is sufficiently large to mainly desintegrate central diffraction maxima. This small fields are still sufficient, since unlike the Schmidt camera, the long-focus configuration are intended for studying individual, generally very small objects. Both are used as spectrographs; the Nasmyth for faint stars and galaxies (Nasmyth spectrograph is mounted on one of the two fork arms), while the Echelle spectrograph at the Coude focus, with 30-100 times higher resolution, is located in the basement of the dome building (it is used for more detailed studies of relatively bright stars). Angular field wise, correction is practically identical at the Coude focus, only the image scale (i.e. linear field) is larger in proportion to the f-ratio. The needed secondary conic is somewhat lower, 6.9733, with somewhat different higher-order terms.

18 - Willstrop-Paul-Baker 5m f/1.6 and f/2.6 wide-field telescopes

Back in 1984. Roderick Willstrop of the Cambridge University Observatory came up with a design for large survey telescopes - a three-mirror system similar in configuration to the Paul-Baker telescope. The later has a great simplicity, using a paraboloid for the primary, and two spherical smaller mirrors to achieve impecable correction over wide field (the flat-field variety uses ellipsoidal secondary). However, large fast systems of this kind generate unacceptable level of higher-order aberrations, setting the relative aperture limit at about f/3 (it varies somewhat with the aperture size). Willstrop found that higher-order aberrations can be greatly minimized, or completely eliminated by putting appropriate higher-order aspherics on all three mirrors. Since it was Bernhard Schmidt who first introduced this type of surfaces, Willstrop presented his new design as Mersenne-Schmidt (Mersenne telescope is a Cassegrain system using confocal secondary, hence producing collimated beams). While it has its merits, the system is still directly related to the Paul-Baker telescope, and hereafter will be referred to as Willstrop-Paul-Baker (WPB) telescope.

The first system, 5m f/1.6 published in 1984., had a curved best field, and the second one, 5m f/2.6 published the following year, was flat-field. In his papers, Willstrop gave a complete prescription for both systems, but they are not usable with raytracing programs. The reason is that Willstrop himself - according to Bob May's page (the other two related articles can be opened by replacing 3 in the address bar by 2 and 4) - didn't use raytracing software, and his prescriptions use forms not compatible with raytracing software, possibly to some extent even personal (for instance, he describes 2nd and 3rd mirror as "approximately spherical", yet the sagitta given with the a2 term implies paraboloid as the base shape for both; the 2nd mirror radius - probably related to the sign of sagitta - is given as a positive number, which in any Cassegrain configuration implies concave, not convex surface, and alike). In order to make prescriptions workable, it was necessary to asign to the 2nd and 3rd mirror the base shape different than a sphere (paraboloid and oblate ellipsoid with eccentricity 1 for the f/1.6 system, and paraboloid and a weaker oblete ellipsoid for the f/2.6) and, of course, to asign to the 2nd mirror a negative radius value. Even then, this was only taking care of the 4th order aberrations; in order to minimize 6th and higher order aberrations it was necessary to tweak the higher-order coefficients. This means that the systems presented here are different in prescription from the original, but they are within Willstrop's main frame, and the correction level is comparable.

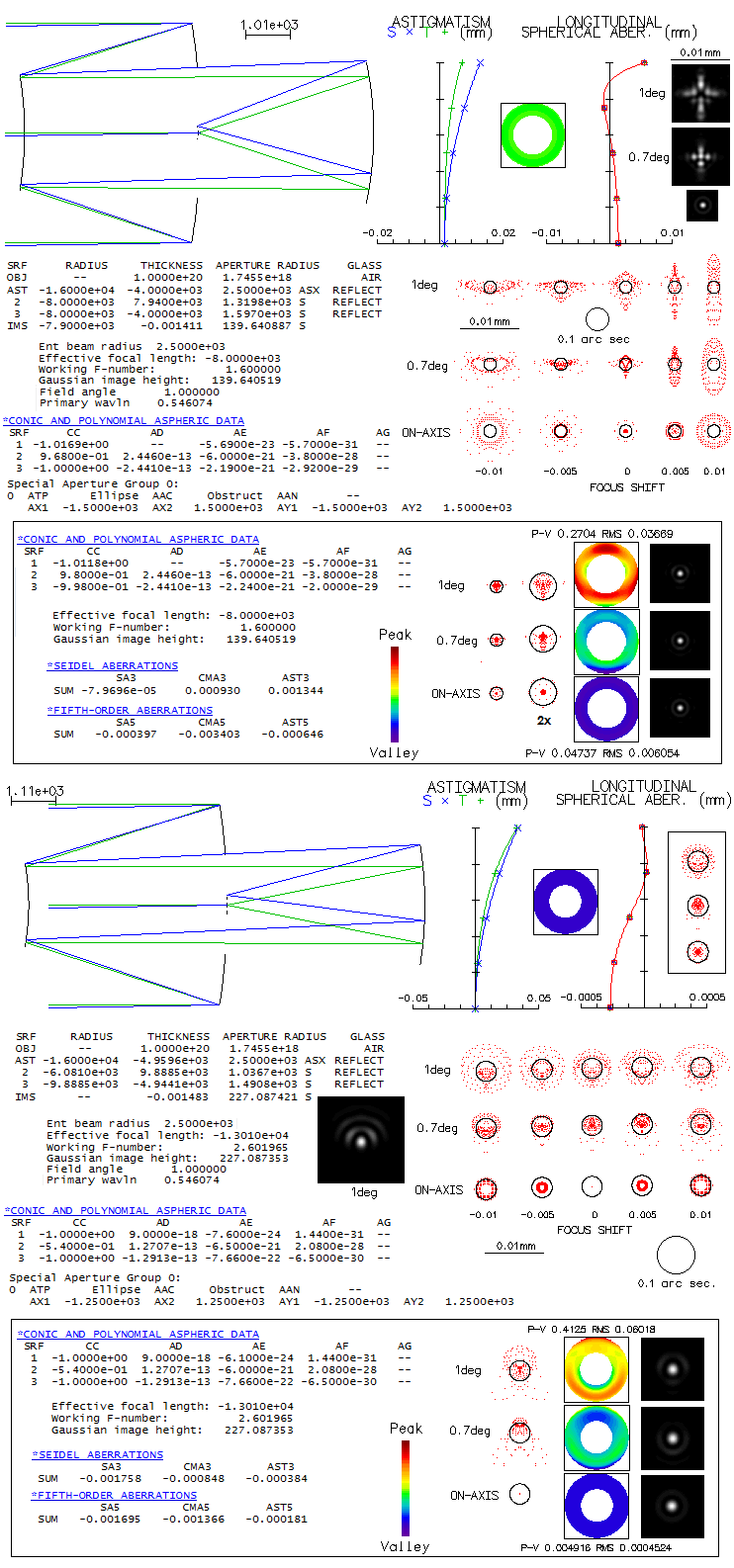
The first system, f/1.6 with a curved best surface (top) has a hole in the primary of nearly 60% the aperture diameter, and it is assumed to be the effective central obstruction. Willstrop gives two versions for the curved field configuration, for 2° and 4° field diameter. Also, for the flat-field version gives spots for 3° diameter, but in either case full illumination is provided only for 2° field diameter. Only the 2° field version will be considered here for the curved-field WPB, as well as 2° field size for the flat-field arrangement (spot size increases significantly in the 4° curved-field version, and beyond 1° field radius in the flat-field arrangement). To demonstrate the fine tuning system performance by balancing the coefficients - i.e. the corresponding aberrations - the first system is shown with a low residual astigmatism, corrected with rather small changes in some of the coefficients (box below).

The second system, f/2.6 with flat best surface, has somewhat smalle hole in the primary, determining the minimum central obstruction to 50% of the aperture diameter. After the initial correction of higher-order aberrations (mainly coma, corrected by changing 4th order coefficient on the secondary for primary coma, and 6th order coefficient for secondary coma, with the resulting spherical aberration corrected by adjusting primary's conic and 6th order coefficient) had some low residual coma left in, not visible in the ray spot plot (bottom), and was corrected in a similar manner (box below). In effect, both systems can be made to be better than "diffraction limited" over 2° field diameter. In general, designs here are shown with minimized spherical aberration on axis. It is not uncommon that allowing for some spherical aberration results in a reduced off axis spots. Box next to the spherical aberration plot shows that introducing a tiny amount of spherical aberration in this case results in a small, but noticeable reduction in the off-axis spot size.

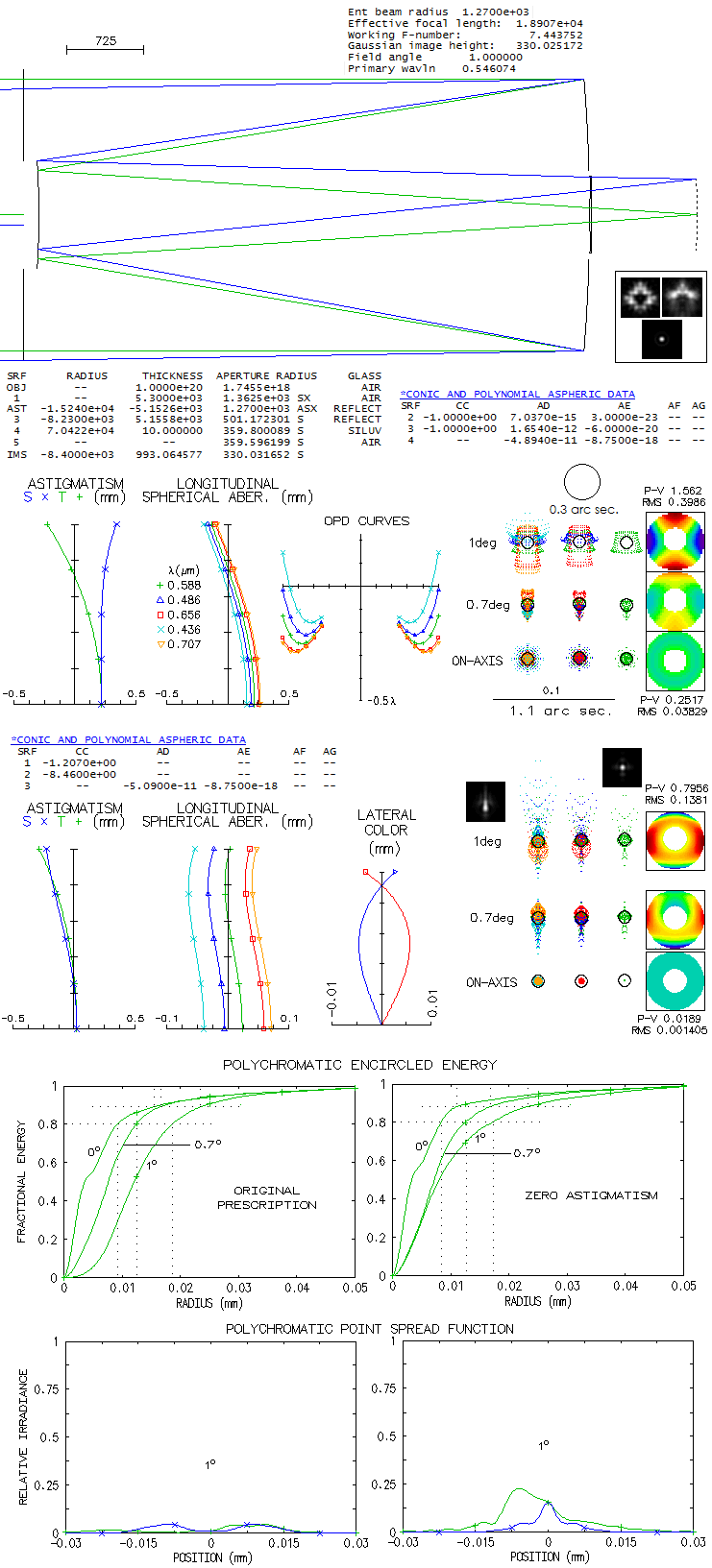
To illustrate how much of improvement it represents vs. Paul-Baker with paraboloidal primary and spherical secondary and tertiary, the f/1.6 configuration would have practically zero 4th order aberrations (except Petzval curvature and distortion, which are the same as in the WPB), but its best focus secondary spherical would be as much as 71 wave P-V, making its ray spot plot 1.2mm in diameter (about half as much for the dense core). With spherical aberration made negligible putting aspherics up to 10th order on the primary, remaining secondary (mainly) coma would be 37 waves P-V (nearly 0.5mm ) at 1° off axis. Putting appropriate higher-order aspherics on the secondary and tertiary significantly reduces blur size (below, top), but the blur is still about 0.02mm, or 1/2 arc second at 1° off axis. While it could be further reduced in final optimization, for "diffraction limited" level - or better - over the field, more higher-order aspherics, as well as conics on the secondary and tertiary are needed.

In the standard Paul-Baker flat-field arrangement with the same primary and obstruction size, secondary spherical (mainly) would have been "only" 5.6 waves P-V, with secondary coma little over 5 waves P-V at 1° off axis (with secondary spherical corrected). Limited aspherizing here is sufficient to achieve very good correction (middle). However, such system would have been significantly longer, and also slower, than the WPB. Viable alternative is to use smaller secondary, which allows for a faster, much more compact configuration with smaller central obstrution (bottom, minimum secondary size 30%, primary hole 50%). Limited additional aspherization results in a good overall correction, and full aspherization, as the one used with the WPB, would further improve correction. As the prescription shows, even if this system is formally flat-field, the actual best field does have not negligible curvature, due to the higher-order Petzval curvature. It can be compensated for by making tertiary radius of curvature weaker - in this case -6960mm, with the secondary-to-tertiary separation made equal to it - which, with small adjustments in some coefficients, nearly reproduces this output on flat field.

A note on the puzzling inconsistency between zero astigmatism showing on the plot, and the apparent significant astigmatism in the diffraction image for the top arrangement. Aberration coefficients also don't confirm presence of astigmatism, yet it is showing nevertheless?! Also, the wavefront maps (central obstruction omitted for clarity) show the presence of a significant off-axis spherical aberration as well!? A look at the coefficients given by Synopsys finds that most of the astigmatic-like deformation comes from oblique spherical aberration, which is nearly twice stronger in tangential vs. sagittal orientation (it is also "helped" by some coma and trefoil). By definition, oblique spherical is secondary aberration identical in form to primary spherical, but proportional to the square of field angle; SYNOPSYS - at least this ancient version I'm using - seems to be misbranding secondary astigmatism as "oblique spherical", while its "secondary astigmatism" could be actually the lateral astigmatism form, also secondary aberration which changes with the 2nd power of field angle and in-pupil height, and 4th power of field radius (unlike 2nd, 4th and 2nd power, respectively, with secondary astigmatism). Zernike coefficients do not include oblique spherical term, since it is not needed, and point to astigmatism as the dominant component of the wavefront error. It seems logical that OSLO uses the same secondary astigmatism form (lateral astigmatism), and does not list the other secondary astigmatism form, which is listed as secondary astigmatism by Mahajan.

19 - 6.5m f/5.36 converted MMT

Multiple Mirror Telescope, with a primary consisting of 6 hesagonal (honeycomb) mirrors, each 1.8m in diameter, was completed in 1979. at the Whipple observatory on Mount Hopkins, Arizona. In 1998. as new technologies made feasible production of large lightweight mirrors, the primary was replaced with a single 6.5-meter mirror of slightly larger outer diameter, but with more than twice larger collection area. New telescope is a versatile, multipurpose instrument with as many as three interchangeable secondary mirrors, providing f/5, f/9 and f/15 focal ratios in a classical Cassegrain design. The widefield, f/5 mode has two configurations, one spectroscopic and the other one imaging. Both use field correctors for achieving wide, well corrected fields. The one presented here is the MMT widefield imaging configuration, as described in a paper by Fabricant, McLeod and West.

By design, field diameter of this version is 35 arc minutes, or just under 0.6° in diameter. It is not particularly wide angularly, but linearly it extends 0.365m in diameter. While in the paper this arrangement goes as f/5 (which is a focal ratio of the bare Cassegrain configuration), prescription given there produces f/5.36 system. Ray spot plots presented here are for the minimized axial spherical aberration - for that purpose the secondary conic was slightly changed - although the actually used imaging plane may be somewhat defocused. Field corrector consists of three lenses, followed by field flattener placed near image plane; in front of the flattener is a glass filter. System is raytraced in the usual visual spectral range, but telescope is used in a wider range, 330-1000nm. Size of central obstruction wasn't specified; considering that the minimum secondary size in this configuration is about 25% of the aperture diameter, it is assumed to be 30%.

Design limit for the central line (here 546nm) exceeds 0.97 Strehl in the field center. The corresponding ray spot plots for the central wavelengths, as well as all five - shown next to the field corrector - indicate excelent longitudinal color correction, confirmed by the tightly woven together OPD plots (the 0.0072mm scale represents the 0.546nm Airy disc diameter). Off axis ray spot plots for angles larger than 0.1° become significantly larger than Airy disc, with correspondingly bloated diffraction pattern. Still, the plots, and the patterns' dense areas remain within 0.05mm, or 0.3 arc seconds circle (for clarity, diffraction patterns are about 25% larger). According to the paper, 80% encircled energy circle diameter averages out at 0.018mm, and 90% EE at 0.024mm - about 0.11 and 0.14 arc seconds, respectively, roughly three times the Airy disc diameter (which is about three times smaller than in the spectroscopic configuration).

20 - 2.5m f/7.5 Irenee du Pont telescope

In operation since 1977 at Las Campanas observatory in Chile, this telescope was designed for direct astrophotography. It is a modified Ritchey-Chretien (RC), which uses single aspheric plate as a field corrector (Gascoigne corrector). Details, including prescription data, are given by its designers (The optical design of the 40-in telescope and of the Irenee DuPont telescope at Las Campanas observatory, Chile, Bowen and Vaughan, 1973.). It is designed to cover field of 2.1° in diameter. Correcting plate removes astigmatism, but induces significant coma, which requires more strongly aspherized secondary (to correct for coma) and primary (to correct for spherical aberration induced by the stronger secondary) than in an all-reflecting RC. The field is moderately curved (9m), requiring bending of the detector. Secondary diameter is 95cm, and central obstruction somewhat larger (not specified), taken to be 40% of the aperture diameter.

Raytrace below (top) shows low residual astigmatism, good color correction and somewhat stronger best field curvature. Part of the difference could be that the published ray spot plots show roughly even spot size across the field, implying that the field was somewhat defocused and/or shifted from the best image surface in order to equilize the spot size. Diffraction images at 1° off - monochromatic (left) and polychromatic (right, even sensitivity for the five wavelength) - and on axis (small box at right of the system drawing) show that the blur at the field edge is smaller than 0.3 arc seconds, as was claimed. For comparison, an RC telescope in this configuration but without corrector would have as much as 59 waves P-V of astigmatism at 1° off axis, on the best image surface, slightly over 1mm (nearly 11 arc seconds) in diameter. Also, best image surface is nearly four times more strongly curved.

Making corrector's 4th order coefficient slightly stronger, reduces astigmatism to zero, producing better corrected outer field (middle). Best image curvature is now 9m, with the chromatic correction remaining, as expected, nearly unchanged (vertical elongation in the diffraction image at 1° would have been somewhat less pronounced with the actual, CCD sensitivity). Encircled energy plots show better energy concentration for the second system (in which the center field error was also minimized), although the difference is relatively small. The respective PSF, however, show what is evident on the diffraction images, that the astigmatism-free version has smaller area of energy concentration, translating to a higher detecting/resolving potential.

Note that the two conic/aspheric data columns appear to differ significantly, but the actual difference is small. The original prescription describes surfaces through the sagita (a2 coefficient times aperture radius squared), adding to it the (conic) a4 coefficient (which multiplies with a 4th power of the radius to produce surface sag which in effect corrects value of the conic), and a6 coefficient (multiplies with a 6th power of the radius for the 6th order surface sag). The a2 value in the original prescription defines a sag of paraboloidal surface as the starting shape, with the a4 coefficient effectively correcting the conic value, and the a6 coefficient addressing the 6th order surface/aberration domain (for instance, taking a4 coefficient for the primary, it gives the conic value from K₁=8R³a₄-1=-1.2, where -1 represents the starting paraboloid; if starting shape is a sphere, the a4 value simply needs to be six times larger to represent -1.2 conic). The other prescription uses simpler notification, defining starting surface shape as a sphere - raytracing default - with a conic alone added (which puts the value of the effective conic correction, a4 coefficient, at zero), with the higher-order coefficients omitted as having relatively small effect (they can clean up the vertical ray scatter, but wouldn't appreciably reduce the RMS wavefront error, nor improve diffraction image). The conic values (obtained from a2+a4 values in the original prescription, and as a conic alone in the zero-astigmatism system) are very close.

21 - 0.7m f/3.2 AZT-16 astrometric astrograph

A telescope with unusual destiny. It is the last observatory telescope for which the optics was designed and superwised by D.D. Maksutov. It is considered one of his best, if not the very best design. In the early 1964. when the optics for AZT-16 ("AZT" stands for "Astronomicheskiy Zerkalyniy Telescop", or "Astronomical Mirror Telescope", and 16 is merely the number in a series of various reflecting telescopes) was in its finishing stage, Maksutov was at the institute around the clock, even slept there, to make sure the optics will be completed (his health was poor, died in August that year). In 1968. AZT-16 was installed at the peak of Cerro El Roble mountain, Chile, to be active till 1973, when due to Pinochet coming to power the Soviet astronomers were forced to leave, with AZT-16 staying behind, conserved. After four decades, Pulkovo observatory, who owns the astrograph, regained access to it. The instrument has been found to be in serviceable condition, but needs modernization/automatization. Chilean astronomers were taking care of it, considering it to be a very special instrument; so much so, that they've put a plate on it, reading: "Este es el Maksutov mas lindo del mundo y sus alrededores" ("This is the best Maksutov on Earth, and in the Solar system").

The AZT-16 uses double meniscus - a positive, and negative one - instead of a single meniscus of the standard Maksutov, with a singlet lens corrector (Piazzi-Smyth lens) nearly touching the image plane. It allows better overall correction, in particular flat field, near negligible lateral color error and better central line correction. The primary is a mild prolate ellipsoid (K=-0.1257), which does allow for somewhat more relaxed meniscus radii (also, as the article mentions, provides the convenience of two foci for testing purposes). A single-mirror system with such field corrector can have either astigmatism or lateral color corrected, but field curvature remains unacceptably large (it requires negative field lens, adding to field curvature of the base configuration), and the overall correction level is somewhat lower. Also, the field remains strongly curved. Maksutov's design flattens the field and reduces all aberrations, with a relatively low higher-order spherical aberration residual remaining (it could be cancelled by putting 6th order aspheric on one of the meniscus surfaces, but wouldn't appreciably improve field performance).

Below is a complete system drawing, showing placement of the front opening, front and rear meniscus (1), 1-meter primary mirror (3) and field corrector (2) in the optical tube assembly. The glass used for all three refracting elements is LZOS K8 crown, a Schott BK7 (used in the raytracing model) equivalent.

AZT-16 prescription was published in an article by Maksutov and his associates (Трудах 15-й Астроннмической конференции, i.e. Proceedings of the 15th astrometric conference, 1960). This prescription, however has an error, as raytrace below shows: central correction is somewhat off and, more importantly, colors are not as tightly bound together as they should be (top, in a box). It is not known to me if correction has been made in that, or some other publication. Nearly all of the longitudinal chromatism is induced by the field corrector, i.e. the two menisci are nearly optimally corrected. But taking the field corrector out increases spherical aberration residual to nearly 0.11wave RMS, from 0.073 wave with corrector, and the possible minimum of 0.064 wave (either with a slight adjustment an a meniscus radius, or by increasing mirror conic to -0.152).

The only way to bring colors together keeping the field corrector is either to change radii on one of the meniscus correctors, or change the thickness and radii of one of them. Since the latter requires more extensive alterations (including making the field lens a positive meniscus), in order to illustrate near peak performance of the design, radii of the rear meniscus vere changed in order to bring colors tightly together, with some minor compensatory changes of some other parameters (including minimizing error in the central line). Resulting system is shown below the box. Field is taken to be 2.3° in diameter, as given in the article, although fields in excess of 5° were used. Central obstruction size wasn't specified, but from above drawing it should be about 1/3 of the aperture. The stop is not given in the prescription, but it is mentioned in the text (460mm in front of the first surface); its effect is minor, as article puts it, it somewhat reduces "tails" of the ray spot plots off axis.

The field is very even correction-wise, with the central diffraction maxima at 1.15° of axis showing only mild elongation due to lateral color error (the five wavelengths, even sensitivity). Encircled energy is even slightly tighter at the edge, than in the center, with the 80% energy circle radius below 6 microns (about one arc second; but resolving limit for contrasty details is, with the central maxima intact, approximately the Airy disc radius, i.e. 2 microns, or 0.2 arc seconds). On axis, such system can be "diffraction limited". Best balance between astigmatism, lateral color error and Petzval curvature (which represents image curvature for zero astigmatism) is achieved by adjusting the thicknes and rear radius value of the field lens.

The above AZT-16 drawing does not agree with the prescription: front meniscus is noticeably thicker than the rear meniscus, and using primary's diameter (1m) as a measuring unit also implies that the primary is faster, with the entire assembly shorter. There is no specifics on the source or date of the drawing on the site, for which is not clear is it related to the Pulkovo observatory. But since it appears to be a legitimate technical drawing of what would be at least a version of the instrument, it deserves consideration. Raytrace (below) shows that the drawing implies an f/2.9 system, not quite as well corrected as the f/3.25, but not significantly worse. The only discrepancy is in the menisci-to-mirror separation, which is about 2.4m according to the drawing, but has to be nearly 0.5m wider in the raytracing model in order to fully correct for coma (both, front and rear meniscus are thicker than in the article prescription, with the radii adjusted to achieve best color and central line correction).

Field lens is thicker, and it is assumed that the lens-to-image separation is somewhat wider (as could be indicated by the drawing). At the 2.8m separation, low residual coma is showing in the diffraction image (monochromatic @546nm left, polychromatic for the five wavelengths, even sensitivity, right) farther off axis. It does not appreciably affect encircled energy, and can be cancelled by moving the menisci 9cm farther out (diffraction images below at 1.15°). There is no displaced stop, as it doesn't seem to be present on the drawing; its effect is very small, anyway. Whether the actual instrument is closer to the first, prescription-based, or the second arrangement, it can be made to be a highly-corrected, low-distorsion flat-field astrograph. OPD curves imply nearly 20% larger chromatism vs. f/3.25 system. Note that the P-V wavefront error on axis (e-line) is numerically inflated due to the manner in which OSLO calculates it in the presence of central obstruction; the RMS error value implies that the actual error is at the level of 1/3 wave P-V of primary spherical aberration. It corresponds to the canonical balanced 6th/4th spherical aberration with the marginal and paraxial foci of the LA graph coinciding. But the actual minimum here is when the two foci are somewhat separated, 0.078 wave RMS (with, for instance, R4=-1152.5mm), probably due to the presence of a not quite negligible 8th order spherical aberration. The overall chromatism is lower to a similar degree.

The main advantage of double meniscus is that it makes possible to flatten field with astigmatism kept negligible. A single-meniscus system with a singlet field lens for lateral color correction can achieve nearly as good correction, but the negative field lens adds to the system's Petzval curvature, leaving as the only option a flat astigmatic field with rather significant magnitude of astigmatism (or aplanatic strongly curved image surface). A f/3.25 system would have somewhat better correction, as shown below (the mirror keeps the same conic, to make systems fully comparable).

The central line is well within "diffraction limited" on axis, and even 1.25° off diffraction patternn is still fully preserved. Most of the 0.3% distortion comes from the field lens. It can be practically cancelled by reshaping the lens, but it would induce other aberrations; however, it is likely that there is systemic solution for yet lower distortion without compromising overall output (the thicker meniscus is probably related to keeping lateral color error low, while optimizing the field lens shape for minimum distortion).

22 - 10m f/7 infrared space telescope: Millimetron

Sub-millimeter and millimeter (far-infrared, FIR) wave range is where most of the progress in our knowledge and understanding of universe is to take place. A space telescope that would span uniquely wide range of radio frequencies, combined with exceptionally large aperture was concieved in the mid 1980-s, in then USSR, and the project carried over to the Russian Federation, as Millimetron space telescope (also known as Spektr-M), due to become operational by 2029. Initially, diameter of the antena was supposed to be 12m, but later on was reduced to 10m. Its spectral range varies somewhat with the source, spanning approximately 0.05-10mm range. It will work as a single dish, and as a part of sub-millimeter space-ground VLBI interferometer, making possible sub-microarcsecond resoultion. It will be able of collecting new information on formation and evolution of planets, stars and galaxies, including processes near the event horizons of black holes.

Among instruments that will be used with it are Mmtron Heterodyne Instrument for Far-Infrared (MHIFI, 0.3-7mm), Short-wave Array Camera Spectrometer (SACS, 70/125/230/375 micron camera, 50-450 microns spectrometer) and Long-wave Array Camera Spectrometer (LACS, 0.4/0.7/1.2/2.3 mm camera, 0.3-3mm spectrometer). Camera covers 1.75'x3.5' field, spectrometer significantly smaller, and it can be as small as 2x2 pixels with heterodyne receiver (data from 2008 paper; actual fields may be somewhat different).

Optical system is classical Cassegrain, consisting from 10m f/0.24 paraboloidal primary and a very small secondary (little over 5% by diameter effective area), for the final f/7 focal ratio (the actual system will employ a diagonal placed behind the primary, but it doesn't affect optical output). Raytrace shows the perfect-system output for the four SACS bands, where the off-axis aberrations are most pronounced. The -150mm field curvature effect is insignificant even at the shortest wavelength. As a curiosity, the system output at 0.588 micron (d-line), over best field surface (bottom right). Making it aplanatic significantly improves off axis performance, as the ray spot plots show (surface conics given at the bottom), but the difference is negligible with much longer wavelengths used by the radio-telescope.

23 - 1m f/4.1 observatory-class wide-field Ritchey-Chretien

Ritchey-Chretien (RC) two-mirror system had become the system of choice for large observatory telescopes. However, its quality field is limited by astigmatism and field curvature, and for that reason observatory telescopes of this type commonly use field corrector to improve field quality when it is needed. For very wide fields, the system has to have large relative aperture, which makes field correction more complex. A paper from Siberian State Aerospace University describes such system, using a Wynne-type integrated field corrector (OPTICAL SYSTEM RITCHEY-CHRETIEN AS PANORAMIC WIDEFIELD TELESCOPE, Veselkov, Zemtsova, Shilova, 2014). Note that the glass in prescription is LZOS K8 crown, which is practically equivalent to the Schott BK7.

Since the corrector is integrated into an optimized system, the mirror conics differ from what they would be in a stand alone RC (-1.292 and -11, respectively). The 1-m primary mirror has somewhat stronger, and the secondary somewhat weaker conic, with the front surface of the corrector also being aspherized. Expectedly, central obstruction is large, around 50% by diameter (assumed in raytracing; minimum secondary size is 41.4%). Prescription given in the paper has a typo, because the final back focus falls more than 4mm closer than specified, and the blurs are larger than those presented. The simplest way to bring the final focus to nearly coincide with the one given in the paper is to make either primary slightly weaker, or secondary slightly stronger. The former gives a bit better result, so the primary radius of curvature is changed from -3553.14mm given in the paper, to -3554.6mm (it also brings the ray spot plots very close to those published). The primary focal length that produces exactly the same back focal length is -3554.885, but it nearly doubles e-line error in the center, and also slightly worsens it at the edge.

The 215mm field is flat and well corrected, with the only significant aberration remaining being trefoil. Due to it, the 80% encircled energy diameter increases from 11 microns on axis to 17 microns 1.5° off. Field edge polychromatic blur is within 0.025mm circle (1.26 arc seconds), and so is the bright part of the diffraction image. Since the bright core is still present, the corresponding limiting field edge resolution is significantly below 1 arc second. For comparison, the stand-alone RC would have as much as 76 waves P-V of astigmatism at 1.5° off, with ~0.6mm blur size (best image surface).

While the longitudinal color correction seems to be at or near optimum, with the colors crossing at approximately 70% zone, and the OPD plot about as tight as it can be, a better overall correction is with the crossing at nearly 90% zone. This is not usually the case, and the main reason it is here seems to be the large central obstruction.

Despite the OPD for this crossing location appearing significantly more stretched out, the corresponding RMS wavefront errors average favor it, producing 0.922 polychromatic Strehl, vs. 0.890 with the 70% zone crossing (the five wavelengths, even sensitivity). The OPD is misleading here, inflated, because it is constructed based on the way OSLO calculates the P-V wavefront error in the presence of central obstruction, where it is measured vs. wavefront center, which practically does not exist. What matters is only the actual wavefront, and how it measures up against the scale.

24 - 4.1m f/16.6 SOAR telescope

Situated on Cerro Pachon, Chile, at an altitude of 2700m, Southern Astrophysical Research (SOAR) telescope is said to be designed to produce the sharpest images possible with a ground-based telescope. It uses active optics on both, primary and secondary mirror, with the rotating flat tertiaty mirror having tip-tilt correction. The mirrors are made of Corning Ultra Low Expansion (ULE) glass. Under average seeing, it enables it to have image quality of ~0.5 arc seeconds at 0.8 micron wvl, and the addition of Adaptive Optics Module (ground layer addaptive optics) in 2013 took FWHM down to 0.25 arc seconds (for comparison, HST resolution is 0.05-0.1 arc seconds). It is a two-mirror system with two Nasmyth foci and three bent Cassegrain foci (which, unlike Nasmyth foci, are not positioned on the altitude axis); prime focus is not accessible. Each Nasmyth focus has a cluster of three interchangeable instruments, plus one instrument on each bent Cassegrain focus. Instruments operate in spectral range from the atmospheric cutoff in the violet at ~0.32 micron, to the near-infrared. Central obstruction is 23% linear, probably the smallest one allowing for efficient baffling. Fully illuminated field with baffling on is 10 arc minutes, or 198mm in diameter.

As an optical system, SOAR 4.1m telescope is just another observatory Ritchey-Chretien. What was puzzling to me was that nowhere in the description there was a mention of field corrector. Is the field small enough not to need any? A closer look shows that this is not the case.

OSLO gives best field curvature radius of 959mm, concave toward diagonal. While the six instruments with widest fields would have at least acceptable outer field quality over the 959mm radius best field (bottom left), only two (5 and 6) would have it over flat field. Considering that Latter on, I saw a passing remark of a new CWFS Acquisition Camera (#6) having also field flattener replaced, which indicates that all of these instruments have individually incoroprated field flatteners. Even if it has the smallest field of all six instrument, its field edge error is 0.052 wave RMS for 550nm wavelength, more than 17nm surface error of the primary (depending on the surface profile, it can be anything from twice as much to 1/4 of it in the wavefront). The entire field could be flattened (and partly corrected for astigmatism) with a simple field flattener; a singlet would exhibit some lateral color in the outer field, but a cemented doublet would perform satisfactorily (bottom right; five wavelengths shown are g,F,e,C and r-line, from light blue to orange, respectively). However, with as many as five different focus locations, there would have to be as many field flatteners, one for each. It was probably better solution to couple up each instrument with its individually taylored flattener.

As a side note, the dominant field aberration over best field is astigmatism, and over flat field it is defocus. Ray spot plot for 0.075° field point over best field is nearly identical in size and appearance to the ray spot plot for 0.024° flat field, yet their respective P-V and RMS wavefront errors differ significantly. Another reminder that the ray spot plot size and appearance is not tightly releated to the wavefront error.

25 - Stanford Observatory 22-inch Maksutov-Cassegrain

This 22-inch Maksutov-Cassegrain was designed by John Gregory, who at the time worked as an optical engeener for the Perkin-Elmer Corporation, where the optics was fabricated. It saw its first light in 1965, and in 2022 was relocated to New Mexico, to a better location. The design is unusual, having two secondary mirrors: one, small, permanenetly mounted onto the meniscus, providing an effective f/15 system with visually accessible focus, and the other, large flip mirror providing f/3.7 system with focal plane in front of the primary mirror for astrophotography. It is among the world largest Maksutov-type telescopes: there are two 70cm systems (both build during the Soviet Union era, one the double meniscus system described above (#21), and the other one is at the Georgian National Astrophysical Observatory near Abastumani), and several 50cm systems, most of them also from that era. However, it could be the largest one that can be used for visual observations, since the double meniscus system is astrograph, and tube length of the other one strongly suggests it is also a single mirror system. Oddly enough, there is almost no information on the design and optical system of these large observatory Maksutov telescopes. The Stanford 22-inch is a partial exception: there is no published prescription, and even the basic information, like focal length of the primary, are missing, but based on the optical scheme, a detailed article by the long time curator of the observatory (A short history of Stamford Observatory, Charles Scovill 1995), and photograps of the actual instrument making possible to approximate element separations, a system similar to the actual one can be reconstructed. The overall dimensions imply quite a fast primary mirror, around f/2.5, which inevitably results in a significant level of higher-order spherical aberration, which can't be affected if keeping surfaces spherical. For that, a higher-order aspheric needs to be put on one of the surfaces and, as the article states, in this case it was the secondary mirrors. In all-spherical arrangement, f/15 system requires somewhat stronger meniscus radii for optimally balancing spherical aberrations, and consequently has a larger residual axial error than the f/3.7 system (0.21 vs. 0.14 wave RMS). The latter could probably function well enough w/o aspherization, with the error remaining nearly unchanged over 0.5° field radius, (aspherization mainly improves inner field performance), but both possibilities will be addressed. The field is practically flat with the f/3.7 system, due to the near-zero Petzval and astigmatism, and is effectively flat with the f/15 system, due to the small angular field. Central obstruction is assumed to be 12cm (0.215D) with small secondary, and 26cm (0.465D) with the large one; it shouldn't be far from the actual values.

The question of meniscus shape seems to be answered with the requirement of corrected coma being imperative for the photographic use. If the starting shape is the one optimal with the small secondary, the f/3.7 system can't be coma free with or without higher-order aspheric. The same applies to the f/15 system if the starting meniscus shape is the one optimal for f/3.7 system (i.e. for having optimally balanced 4th and 6th order spherical), but coma would in this case be acceptable, not affecting appreciably visual observation (and for the small secondary it seem to be causing astigmatism, as shown little later). Thus, starting with all-spherical f/3.7 system (below, top), it does have an overall acceptable correction for photographic instrument, the only exception being lateral color error in the outer field. It doesn't affect the encircled energy value, because a lot of energy is spread away from the central maxima (which is still clearly defined, and smaller than that in a perfect aperture, as it is with spherical aberration), but it would cause severe elongation of the star image. It can be corrected with a negative singlet placed close to the focal plane, without inducing significant other aberrations, and it is probably what was done in the actual instrument.

As mentioned, putting higher order aspheric on the secondary mainly benefits the inner field correction, which may, and may not be significant, depending on target. The reason is that adding 6th order term induces higher-order coma, which is different in form than its lower-order cousin, hence the two doesn't cancel out completely. The higher 6th order term, the more of this residual. At the 6th order term value needed to reduce 6th order spherical to zero, the field edge error woul have been more than twice larger than without it. Best approach seems to be to do only a partial correction of the 6th order aberration, without significantly worsening field edge correction (bottom). Optimizing such system would call for minor changes, in this case reducing meniscus-to-primary separation by about four inches, requiring reduction of the conic from 1.86 to 1.6 (conic can be approximated with a corresponding value of the 4th order coefficient, i.e. 4th order curve, according to CC~8[AD]R³, which is nearly identical for all but very strongly curved surfaces; in the bottom system above, the effect of 1.6 conic is practically identical to that of -7.4^-12 4th order term). Chromatic correction is significantly better across the field.

If, keeping the same meniscus, large secondary flips down exposing the small secondary, which only has conic added to optimally re-balance 4th and 6th order spherical, correction is poor, at a level between 1/3 and 1/2 wave P-V of primary spherical aberration on axis (below). Adding higher-order aspherics to remove higher-order spherical aberration results is still nearly flat field, with significant astigmatism toward the edge (bottom right, boxed). Here, again, plausible option is a partial correction of 6th order spherical, and better outer field correction.

A closer look at the two secondaries - specifically at their aspherization - shows that the large secondary needed somewhat peculiar shape, due to its large size effectively making the deviation in the 4th and 6th term very similar in magnitude. In fact, when the coefficient value multiplies with d⁴, i.e. d⁶, respectively (d being the surface radius) they give nearly identical edge deviation. Since the two are of opposite sign, this means that no glass is to be taken off the edge. Unlike the conic curve (here parabola) vs. sphere, where deviation changes smoothly, aspheric on the secondary deepens toward the edge forming a wrinkle to meet the sphere at the edge (aspheric curves are greatly exaggerated, in order to show the profile shape). Due to the two aspheric factors (8th order factor can be neglected in that respect) having nearly identical maximum deviation, there is no difference between the paraxial and best focus correction, since the quadratic terms in the two respective best focus relations, x⁴-x² and x⁶-x², cancel each other out for any zonal height, reducing to the paraxial focus relation x⁴-x⁶. So, if the f/3.7 secondary had higher-order aspheric put on, it would have this type of profile.

Unlike the large secondary, the small one has 4th vs. 6th order deviation closer to their usual relative magnitudes, i.e. the 4th term deviation significantly larger. As a result, when aspherizing is done using direct terms (i.e. x⁴ and x⁶, for correction at the paraxial focus), it requires aspherization that removes glass in even progression toward the edge (top). For the best focus correction (x⁴-x² and x⁶-x²), just as in the case of parabolizing sphere, aspherization requires removal of significantly less glass, with the process being inverse to that of parabolization (instead of flattening 0.71 zone with a concave surface, here the ~0.6 zone is left untouched, with the removal increasing toward center and edge; note that raytracing can just configure surface without changing position of its vertex, but with a real glass surface aspheric profile needs to be shifted so that it is entirely within the glass).

Overall, putting a higher-order curve on the secondary is the easiest way to reduce the 6th order spherical aberration residual, but it is limited by generating higher order coma. Putting higher-order aspheric on the primary doesn't have that limitation, and putting it on the meniscus (as in Maksutov's "Astronomical Optics"), is still better. Roughly, higher-order coma in a large, fast Maksutov system fully corrected for 6th order spherical aberration is several times larger with the aspheric on the secondary vs. primary, and the later has it twice larger vs. aspheric on the meniscus. In general, the latter two can have coma minimized by relatively small changes in the miniscus-to-mirror separation, while it would be much more challenging with the aspheric on the secondary. But that is a formal point of view; in practice, a complete correction of the higher-order spherical aberration is usually not necessary, or may not even be desirable. Chances are, the unique 22-inch Maksutov designed by John Gregory was fit to meet its tasks. Non-design factors, such is the inhomogeneous meniscus glass, or turbulent air above observatory building didn't help, but that is different story.

POST SCRIPTUM: After finishing above analysis, I came to realize I forgot what was mentioned earlier, about best focus change in presence of large central obstruction, particularly with Maksutov systems with a relatively significant 6th order spherical aberration residual. Best focus shifts away from the location w/o obstruction and, consequently, the LA graph for best focus location is tilted to the left. So, leaving raytrace at the best focus w/o obstruction for illustration of the effect, here's what the large secondary system (small secondary does not cause appreciable focus shift) looks like for the system at its actual best focus.

Correction significantly improves across the field with all-spherical system (left), coming fairly close to "diffraction limited" 0.80 Strehl on axis (that same RMS wavefront value would with primary aberrations produce ~0.78 Strehl, but balanced 6th/4th order spherical aberration, due to the high slope areas on its wavefront, has less favorable phase, i.e. wave interference). Putting higher-order aspheric on the secondary still improves inner field correction, but at a price of less well corrected outer field, due to the higher order coma induced by the aspheric (right). The all-spherical system is, overall, probably better for imaging, which would imply that the large secondary was probably left spherical. Note that in both cases meniscus radii are slightly more relaxed, in order to optimize longitudinal color correction.

26 - APM 20-inch f/8.5 Maksutov-Cassegrain

This is an example of a modern large Maksutov-Cassegrain. While APM mainly markets commercial telescopes, it also does smaller observatory instruments. Prescription was posted online back in 2017. on multiple sites. At that time, the telescope was in pre-production phase, with a prototype made. Mostly due to a massive mount, the quoted price was quite high: $300,000. However, online search does not return any more recent information on this telescope, hence it is unknown wheter or not there is such unit(s) in operation. Regardless, it is worth a look, and can be also compared with its older cousin: the Stamford Maksutov-Cassegrain above.

At f/8.5, the system is somewhat faster than the usual Maksutov-Cassegrain, with still moderately large central obstruction (D/3). The prescription does not mention aspherics, so the starting point is an all-spherical system. With 0.91 axial Strehl in the optimized wavelength, and somewhat soft outer field correction, it is acceptable, but leaves something to be desired (below, top). Correction can be improved by putting aspheric on any of the four surfaces. One indication that it was done is the thinner than the standard D/10 meniscus; it does generate less of lateral color error, but also adds to the spherical aberration residual. The former remains beneficial, and the latter doesn't matter if spherical aberration is corrected using aspherics. Trying with aspherized primary, or secondary, or meniscus, shows that the higher order coma - a consequence of using 6th order term to remove 6th order spherical aberration residual - is nearly optimally balanced with the 4th order coma (necessary to minimize the overall coma residual) with the aspheric on the secondary, but not when it is on the primary, or meniscus. 6th order coma nearly doubles when aspheric is on the secondary vs. primary, and is nearly six times higher vs. meniscus. Field correction remains nearly unchanged, since with given meniscus' radii 4th and 6th order coma are more out of balance with aspheric on the primary, and still more with aspheric on the secondary (in other words, less of 6th order coma is offset by more of 4th order coma). Since it is easy to manipulate 4th order coma by balancing 4th order term with one of the meniscus' radii, it implies that the likely aspherics were put on the secondary.

For full correction of higher order spherical aberration are needed 4th, 6th and 8th term. Keeping the published radii, chromatic correction is slightly overcorrected in the blue/violet, but it is still excellent. Off axis correction is better, due to the removal of spherical aberration, with the best image surface having significantly stronger radius than the best astigmatic surface (generally, due to the presence of other off axis aberrations).

However, despite the aberration coefficients for 4th and 6th order coma being nearly balanced, the edge point wavefront still shows presence of deformation similar to unbalanced coma, and the diffraction simulation confirms it. Taking a closer look of the OPD graph, the deviation is similar to unbalanced coma (bottom left; for some reason, OSLO gives it uncorrected for tilt, so the dashed line approximates reference line for wavefront deviation with tilt corrected). It is different from the shape of ballanced 6th/4th order (bottom left corner, boxed). The culprit are other off axis aberrations, most likely astigmatism (primary and secondary), tertiary coma and the ever elusive oblique, or lateral spherical aberration (showed by Synopsys as roughly half the magnitude of the 4th and 6th order coma combined), undoing the coma balance. The solution is obvious: since the wavefront has nearly comatic shape, the two coma terms need to be rebalanced, effectively adding more of coma needed to minimize the existing wavefront deviation. It is 4th order coma that can be manipulated, and since it has the same sign as the existing wavefront deviation, it was lowered by lowering the 4th order term, to effectively add 6th order coma in the amount needed to minimize the deviation (4th and 6th order coma have a similar profile). Disbalance it caused in the spherical aberration correction is compensated for by slightly changing the rear meniscus radius. Graph in the middle shows the corrected wavefront at 0.3°, along the axis of aberration (coinciding with the vertical cross section of the wavefront map). Field correction significantly improved, as can be seen on both, the ray spot plot and diffraction simulation (with aspheric on the primary, off axis error would be about two and a half times lower, due to the 6th order term on it inducing less of 6th order coma; with aspheric on the meniscus the error would be still lower, however, aspherizing primary or - more so - meniscus, is significantly more involved).

For optimized color correction, the two meniscus radii would have to be slightly stronger, which suggests that this optimization step didn't take place in the actual design. Axial color correction is close to the optimum, with the blue/violet end overcorrection nearly eliminated (it is easy to accomplish with a slight change in the two radii). The overall correction is better than with the Stamford Maksutov, but for a fair comparison they should be using primary mirror with identical f-ratio (f/3.1 APM vs. f/2.5 Stamford), and a similar size secondary.

27 - 1-m f/15 RAFTER ring telescope

Designed for high-precision astrometry, this peculiar arrangement is derived from Korsh's TMA (Three-mirror anastigmat, which are also aplanatic) analisys. RAFTER stands for "Ring Astrometric Field Telescope for Exo-planets and Relativity", as described in a paper by Riva et al. (2022). As illustrated below, detector area is a small fraction of the available image area. Purpose of the very narrow annular field is to preserve near constant signal response for points separated by up to 2 degrees, as a condition for astrometric precision down to a fraction of the diffraction image. Detector area is 3.4 arc minutes (14.4mm) wide, i.e. 0.25 sq. degrees, containing 66 4000x4000 50mas-pixel detectors (mas=milliarcsecond, 1/1000 of arc second, in this case implying 3.4-micron pixel).

As the ray spot plots show, correction across the entire illuminated field is well within "diffraction limited". Distortion is significant over 1-degree field angle, but about 25 times smaller over the detector ring. Central obstruction is not specified, but it is close to 60%. It is caused by secondary and tertiary mirror - the latter being somewhat larger than the opening in the primary needed to accommodate the image-forming light beams - with the flat merely obscuring the mid-field, and causing some vignetting between the 0% and 100% illuminated field areas.

◄ 14.2. ATM telescopes   ▐    14.4. Commercial telescopes ►

Home  |  Comments