◄ 10.2.3.3. Maksutov-Cassegrain   ▐    10.2.3.5. MCT off-axis aberrations ►
 

10.2.6.4. Maksutov-Cassegrain aberrations: axial

Aberrations of the Maksutov-Cassegrain system are a sum of the aberrations of the meniscus corrector and the two mirrors. In that sense, they are no different than system aberrations of a Schmidt-Cassegrain, given with Eq. 113-119, with the only difference coming from the aberrations induced by a corrector. System aberration coefficients for two mirror systems with meniscus corrector are found from the sum of the coefficients for the three system elements. The main difference, as already mentioned, is that higher-order spherical aberration (HSA) is significantly greater with the meniscus-type corrector, making the third-order expressions for spherical aberration more approximate even with relatively slow mirrors. Designing a two-mirror Maksutov-Cassegrain is considerably more calculation extensive also due to the relatively significant corrector power.

Lower-order spherical aberration (LSA) of a two-mirror system with full aperture Maksutov-type corrector is a sum of spherical aberration contributions of the corrector and two mirrors. Thus, the system aberration coefficient can be written as s=sL+sP+sS, with sL, sP and sS being the aberration coefficients for the meniscus, primary and secondary mirror, respectively. The system wavefront error is given as W=sD4/64 as the best focus P-V wavefront error (D being the aperture diameter).

Lower-order spherical aberration aberration coefficient for the meniscus is, according to Eq. 121.1, approximated by:

with the meniscus focal length ƒL=-n2R1R2/(n-1)2t, and the lens center thickness t=n2(R1-R2)/(n2-1), n being the glass refractive index, R1 and R2 the front and back surface radius, respectively. Since the lens focal length ƒL is numerically negative, the meniscus aberration coefficient is numerically positive, expressing over-correction. As already mentioned on the camera page, this approximation gives a few percentage points larger than the actual value for the third order term alone, but for ~ƒ/3 primary mirror typical for the MCT configuration, it is near exact for the first two terms (lower- and higher-order) combined. Also, due to its greater center thickness, it acts more like a thick lens, with more of the lower- and higher-order aberration generated at the rear surface than what the thin lens concept implies. As a consequence, the actual aberration of the meniscus is some 10-15% lower than what the above approximation gives.

For the primary, the lower-order aberration coefficient is given by

with K1 being the primary conic and σ the corrector-to-primary separation in units of the primary's radius of curvature RP. The p factor p={1+[(n-1)t/nR1]+(σRP/ƒL)}4[1-(RP/ƒL)]2, with σ being the primary-to-corrector separation in units of the primary's radius of curvature, shows dependence of the primary's aberration contribution on the corrector power and location vs. primary, which determine both, ray height at the primary (the fourth power term) and the effective object distance for the primary due to the ray divergence by the meniscus (the quadratic term). The second factor in the fourth power term expresses the increase in ray height at the rear corrector surface, due to refraction at the front surface, which is compounded by the ray height increase due to the corrector-to-primary separation, expressed by the third term. As mentioned, the quadratic term expresses the drop in the aberration level at the primary due to the ray divergence caused by the corrector, effectively placing object for the mirror at the distance approximated by the corrector's focal length.

   This p factor is neglected in calculations for the single-mirror system (Eq. 122-125), because it partly offsets with the factors neglected in Eq. 121.1, thus making the approximation more accurate. It will be, however, included in the two-mirror system consideration, because the ray height factor is roughly cut in half due to reduced corrector-to-primary separation which, with the increase in the effective object distance for the primary due to the weaker corrector, sufficiently reduces offsetting between these factors to make them significant.

The purpose of going through the Maksutov two-mirror system aberration coefficients is primarily to show how it generates the aberrations, not to have them precisely calculated; as already mentioned, due to the likely significant higher order terms generated (mainly) by the corrector, this cannot be done by calculating the third-order aberrations alone.

For spherical primary K1=0 and the aberration coefficient is approximated by sP~p/4R3. It is numerically negative (under-corrected), opposite in sign to the lens aberration.

For the secondary, the aberration coefficient expression is identical to that for the SCT secondary (Eq. 113.1). However, due to the relatively significant negative power of Maksutov corrector, all three parameters, height of the marginal ray at the secondary k (in units of the aperture radius), secondary radius of curvature in units of the (effective) primary's curvature radius ρ and secondary magnification m, have changed with respect to those for the two mirrors alone. The increased height of the marginal ray at the primary, coupled with the slight reduction in its effective relative aperture, results in the increased height of the marginal ray at the secondary as well, and larger k. While to the primary's nominal focal length is effectively reduced by a factor of ~[1-(σR/ƒL)], the actual cone length is larger by a 1/(1-RP/ƒL) factor (FIG. 188), hence the effective ρ' is slightly smaller than ρ, and the effective secondary magnification m' is larger than that for the mirrors alone. So the system aberration coefficient for spherical aberration can be approximated as:

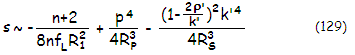
with the first, second and third term being the aberration contribution of the meniscus, primary and secondary mirror, respectively, and R1, RP and RS the radii of curvature of the first meniscus surface, primary and secondary, respectively. The relation is for spherical surfaces; conics can be added, as given for the SCT primary and secondary. Contributions of the meniscus and the secondary are of the same sign (positive), and opposite to that of the primary. For given primary mirror, the system needs to be configured so that its aberration contribution is cancelled by those of the meniscus and secondary. With R1/R2~1, the meniscus' focal length is approximated by ƒL~(nR1)2/(n-1)2t, and the needed first meniscus radius - after substituting ρ'RP for RS - can be approximated as:

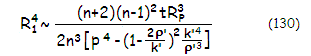
The extraction is not straightforward, as all three of the secondary's parameters are affected by the corrector's power, an unknown beforehand. Probably the simplest initial configuration can be arrived at by starting out with the primary and meniscus alone. Taking again R1/R2~1 and ƒL~(nR1)2/(n-1)2t, the meniscus lens focal length ƒL is approximated in units of the primary radius of curvature as:

For n~1.5 and the average value for p1/2 of ~1.1, it gives the meniscus focal length ƒL~3(RP3/t)1/2, which in turn gives the appropriate front lens surface radius as R12~3(n-1)2(tRP3)1/2/n2 or, for n~1.5, R12~(tRP3)1/2/3. The rear corrector radius for best chromatic correction is, as before, R2=R1-[1-(1/n2)]t/0.97, t being the corrector center thickness.

This gives the first approximation of the meniscus radii needed to correct primary's spherical aberration. Adding the secondary offsets more of the aberration of the primary, requiring somewhat weaker corrector for the system. The degree of weakening can be approximated, most simply, by neglecting the corrector for a moment, and figuring out the aberration coefficient for secondary mirror that would be produced by a system similar to the intended MCT in regard to the relative aperture, obstruction ratio etc. (the level of aberration will change on both mirrors after the introduction of meniscus lens, but the proportion will not change by much). The resulting ratio of the secondary to primary aberration contribution, given by s'~sS/sP (Eq. 154), approximates the ratio of reduction in the needed corrector's contribution vs. that needed for primary mirror alone. Since the aberration contribution of the corrector is (approximately) inversely proportional to the 3rd power of R1, (4th power before factoring in the R1 term in the corrector thickness t) the above value for the front lens radius needs to be increased by a factor of [1/(1+s')]1/3.

The above procedure would result in the first outline of a system, most likely not yet at the optimization level. The main reason is that the meniscus radii approximation would nearly cancel the lower-order spherical, which leaves higher-order spherical aberration - significant with faster mirrors - unbalanced. Thus, radii adjustments are needed to produce usable system. Since it is normally the corrector's properties that need to be adjusted in the first place, the calculation is complicated due to the changes at the corrector causing changes in all other parameters down the optical train: p, k, ρ and m, hence in the aberration contribution of the two mirrors as well. In order to maintain needed geometric properties of the system, effects induced by the adjustments of the corrector's power need to be compensated for with the appropriate changes in mirror separation. Obviously, the two-mirror Maksutov system is more complicated than the single-mirror system, and warrants even more the use of ray tracing software for system optimization and final verification.

Still, MCT system approximation that usually needs only minor optimization can be determined using empirical relation given for the Maksutov camera. The needed front corrector radius for the primary mirror alone is determined from Eq. 126 and Eq. 128 (slightly modified Eq. 128, as R1~[1-2τ-0.01F)R1" should be better suited for faster MCT primaries). This value is then corrected for the aberration contribution of the secondary mirror, by multiplying it with [1/(1+s')]1/4 - noting that s' is according to Eq. 154 numerically negative - and the rear radius value is then obtained from Eq. 128.1. It can be all summarized in an initial approximation for the corrector surface radii given as:

As shown in the section on off-axis aberrations, coma and astigmatism are inherently low in the typical MCT system (k~0.25, m~4) with separated spherical secondary.

In the arrangement with an aluminized spot on the back of the corrector that acts as the secondary (Gregory-style), R2=RS and R1=R2-[1-(1/n2)]/0.97. As mentioned, achieving needed level of the compensatory spherical aberration at the corrector here requires more strongly curved - hence smaller for given back focal length - secondary, producing more of coma and astigmatism. The common radius constraint of this arrangement can be illustrated by substituting n~1.5, R1~0.95R2, t~R2/14, σ~0.4, R2=ρRP, ρ=mk/(m-1)=(1+η)m/(m2-1), and setting RP=1 and back focal length η=0.3 in Eq. 129. Relative aberration contributions of the three elements (in units of RP) now can be approximated as:

1/400ρ3-0.28+1.34/2(m+1)4ρ3 = (m2-1)3/880m3-0.28+(m2-1)3/1.5(m+1)m3

for the meniscus (blue), primary (red) and secondary mirror (green). Plots at left illustrate how the primary spherical aberration contributions of the three Gregory-Maksutov optical elements determine secondary magnification at which the sum will be zero (about 6-inch aperture with the standard ~ƒ/3 primary and ~0.1D meniscus thickness).

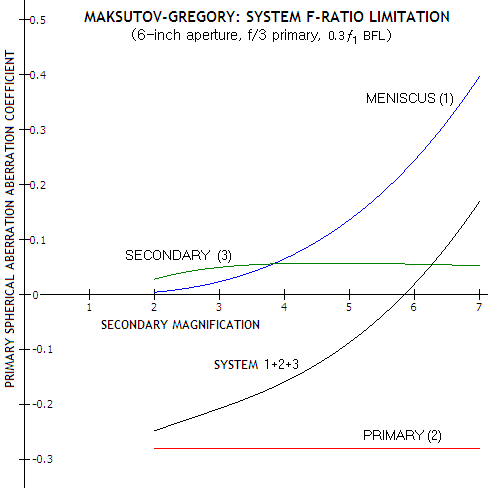The primary mirror undercorrection contribution is nearly constant (it does change but only slightly with the meniscus' radius/power). Secondary's overcorrection is fairly constant for secondary magnifications larger than 3, due to the effect of smaller secondary being mainly offset by the effect of stronger surface radius.

It is overcorrection of the meniscus that changes rapidly with its radii strength - as the relation at left indicates, approximately with the third power of it.  At low secondary magnifications (i.e. large secondary with weak radius of curvature, imposing it onto rear meniscus surface) it is near negligible. Even at m~5, it is still not sufficient to result in near-zero system coefficient, with the system having about 2 waves P-V of undercorrection.

The zero sum occurs at the secondary magnification of ~5.8, i.e. system focal ratio ~ƒ/17.4. The zero-sum secondary magnification doesn't change significantly with faster primaries; at ƒ/2.5 it is still about 5.8 (for the same nominal BFL, nearly 140mm, which is about the practical minimum for this aperture; thus it does decrease somewhat for the same relative BFL). Increasing corrector thickness beyond the standard ~0.1D (D=aperture diameter) lowers the minimum secondary magnification only slightly within the practical thickness range.

    Note that the above consideration is for chromatically corrected meniscus that is corrected for both, spherical aberration (as minimized secondary spherical) and chromatism. Spherical correction - in the form of minimized spherical aberration - can be achieved for any rear meniscus radius - i.e. back focus - value with the appropriate front radius, but for given meniscus thickness there is only one radii combination that will correct both, spherical and chromatism. At secondary magnifications lower than the above minimum, meniscus corrected for both does not have enough of rear side curvature to create sufficient back focus distance.

   Extending BFL by a slight reduction in the corrector-to-mirror separation will also increase the secondary magnification and system focal ratio. The effect on spherical correction is minimal, and can be compensated for by a slight change in the front meniscus radius value. In practice, this means that the range of secondary magnification for the optimum correction extends to up to 10%, or so, above the secondary magnification for near-minimum BFL.

    Similarly to spherical aberration, chromatism can be corrected for any rear meniscus radius value, but with a weaker than needed rear radius (i.e. lower secondary magnification) spherical aberration will not be. Solution to it is to aspheize the primary, which would also allow use of somewhat faster primary (thus more compact design), since correcting residual spherical even at the secondary magnification of about 4 requires significant aspheric (up to -0.4, or so, conic) on the primary, and that in turn allows for a weaker corrector and less of the higher-order spherical residual.

An interesting aspect of the commercial Maksutov-Cassegrain is the question of its star test. There is a notion that its optics has special properties, making it sort of exception in that its intra and extra focal pattern are not supposed to be identical, even when it is near perfectly corrected. Or, put somewhat differently, that it doesn't need to have near-perfect star test for near-perfect performance.

The answer to this special status is in its higher order spherical aberration. Due to its steeply curved optical surfaces, especially those of the meniscus corrector, Maksutov-Cassegrain systems generate 6th-order spherical aberration that can't be cancelled (w/o aspheric surface terms), only minimized by balancing it with the 4th-order aberration. While roughly as much noticeable in the star test as the lower-order spherical aberration for given P-V wavefront error (FIG. 189), the balanced form is considerably less detrimental to image quality.

In an MCT, the higher-order aberration originating mostly at the corrector, needs to be minimized by balancing it with a similar amount of lower-order aberration. Ideally, they are near-optimally balanced one against another, in which case the error reduction factor is about 0.2 (1/5 of the HSA aberration RMS error alone, balanced with nearly identical amount of the opposite in sign LSA). Thus, if an MCT system is, say, 0.95 Strehl, it has ~1/28 waves RMS of combined higher-and lower-order aberrations. In a near perfectly balanced system, each form alone would be over 1/6 wave RMS. Of course, it is possible that the two are less than perfectly balanced, which makes quantifying the star test more difficult, unless the higher-order component is clearly dominant, when it tests similarly as LSA.

The difference between balanced higher-order (BHSA) and lower-order (primary) spherical aberration (LSA), at a similar error level, is that the former affects contrast at lower MTF frequencies somewhat more, and those closer to the mid-range somewhat less than LSA. This is due to BHSA's more steeply curved wavefront edges, causing energy transfer farther away from the Airy disc.

This mysterious property of the seemingly compromised star test combined with an excellent performance level, is also characteristic of other systems with steeply curved optical surfaces, like apo refractors. Schmidt-Cassegrain telescopes also can have the higher-order component present, if the higher-order term is not accurately put on the corrector.

◄ 10.2.3.3. Maksutov-Cassegrain   ▐    10.2.3.5. MCT off-axis aberrations ►

Home  |  Comments