telescopeѲptics.net   ▪   ▪   ▪  ▪ ▪▪▪▪ ▪ ▪  ▪   ▪    ▪     ▪      ▪       ▪        ▪         CONTENTS
 

◄ 8.4.4. Off-axis Newtonian   ▐    9.1  Refracting telescope objective: Achromats ►

In addition to the effect of secondary spectrum, this section will give more details on the effects of monochromatic aberrations and spherochromatism on the refracting telescope performance. There are many types and variations of refractors, but the consideration here is limited to the general case of a contact doublet (FIG. 141), or triplet objective, either achromat or apochromat. In a well executed lens objective the only significant aberration can be chromatism, with moderately curved field and low-level field astigmatism. Misalignment induces primarily coma (tilt/decenter), while despace induces spherical aberration.

FIGURE 141: Refractor doublet objective, contact type, in its standard form with positive front lens and negative rear lens. The final image is formed by the negative rear lens, which is in effect re-imaging the image formed by the front lens to the final focus. The fictitious image formed by the front lens at F1 can be considered to be the object for the rear lens, and the final image is real as long as the front lens has more power; the top point of the (reversed) final image at F is formed at the intersection of the chief ray, which can be approximated as passing through the doublet's center point, and a ray extended from the focus of the negative rear lens F2 (when the two lenses are of identical opposite powers, the two are nearly parallel, and the image forms at infinity). Depending on glass types used for the objective, chromatic correction of a lens doublet can be anywhere from an ordinary achromat level to that of an apochromat. Astigmatism and spherochromatism are negligible in long-focus systems, but may become significant at larger relative apertures.

For over a century since the first recorded refracting telescope with a singlet lens was invented, the only significant advancement to it was that by Johannes Kepler, who just a few years later, in 1611, explained its working principles, and proposed significantly better configuration, replacing the negative eye lens of the Galilean refractor with a positive one. In order to minimize chromatism of a single-lens objective, refractors of this type grew in length well beyond practical limits, but their aperture remained quite limited: the 57mm 11-foot lens with which Christian Huygens discovered Titan in 1655 was comparable to a 100mm f/3.5 achromat chromatism-wise. His largest, 8-inch 210-foot lens had chromatism comparable to that in today's 100 f/6 standard achromat (these are two different forms of longitudinal chromatism, primary vs. secondary spectrum, respectively, but the comparison is possible via polychromatic Strehl). Similar instruments used by Cassini, Hevelius, and others have the same limitations, and were very difficult to use.

The idea that two lenses of different glass types can help break through severe limitations imposed by chromatism came from Chester Moor Hall in the 1730s. He may had a few small refrators made for him according to his invention, but it is unclear how achromatic they actually were. It wasn't until John Dollond had it patented in 1758, that doublet achromat came to life (commonly referred to as "Dollond", but the ~1800. replica of his 50mm refractor has engraved "Dolland, London"). Dollond may had heard of Hall's invention before patenting his doublet. Prior to its pattent application, Dollond did read a paper by Swedish astronomer and mathematician Samuel Klingerstierna, describing theoretical principles of doublet achromatism (he also had correspondence with Euler, who was experimenting with achromatism). Since then, a number of doublet types have been developed, with various levels of correction of chromatism and monochromatic aberrations.

Details of the secondary spectrum and field curvature of a doublet are given elsewhere. Doublet's monochromatic aberrations are a sum of the aberrations of each lens. They are commonly expressed in terms of lens shape factor q and position factor p. Since the two lens elements of a doublet can be considered a thin lens (i.e. one whose thickness is negligible with respect to object  and image distance), at least in first approximation, aberration coefficients for primary spherical aberration and coma for either doublet lens are given by Eq. 8 and Eq. 14.1, respectively; once the coefficients are known, the corresponding wavefront error is found from Eq. 7 and Eq. 12, in the same order.

The same principle applies to the triplet objective.

Graph below (FIG. 142) illustrates the relation between these two aberrations, lens shape and object distance, for the lens' refractive index n=1.5 (common variations in the index value do not affect form of the graph, which remains parabolic, only cause relatively small changes in its vertical position). Minimum spherical aberration for any given lens shape q varies with the position factor p (relative object distance); for n=1.5, spherical aberration is at the minimum when qmin=-(5/7)p, with the corresponding aberration coefficient s=[9-(3p2/7)]/32f3 dropping to zero for |p|=√21. Thin lens is coma free when q=-0.8p, which means that a coma-free thin lens corrected for infinity (p=-1) will also have near minimum spherical aberration.

That would apply to the front lens of a doublet; for the rear lens, the object is the image formed by the front lens, so its p value - and the coma-free shape factor q - varies depending on whether the lens is positive (p~0) or negative (p>1). Correspondingly, q~0 for cancelled coma and minimum spherical aberration for the positive rear lens, and q<-0.8 or q<-(5/7) for the negative. For the usual negative rear lens, with the front lens' image somewhat inside its focus (thus, according to FIG. 69, with the position factor p somewhat larger than 1), the corresponding zero coma (and near minimum spherical aberration) shape factor q is roughly somewhat over -2.

A q~0.8 shape factor makes the front lens biconvex, with the strong first radius and weak second. The q<-2 makes the rear lens a negative meniscus, convex toward the front lens. Coma of such a doublet is negligible, but spherical aberration is still very large. Most of it comes from the front lens which, despite being near its possible minimum, is still extraordinarily high (for instance, in a 100mm f/10 doublet  like this, it would be near 18 waves P-V). For that reason, the approach in designing a doublet is different; in  principle, the two lenses are shaped up so that their spherical aberration and coma (for an aplanat), very significant at each element separately, nearly cancel out when combined.


FIGURE 142: Primary spherical aberration and coma of a thin lens, given as a product of the aberration coefficient (s and c, respectively) and the focal length factor from the coefficient relation (Eq. 8 and 14.1, respectively, for n=1.5) as a function of its shape factor q, for given values of the position factor p. Spherical aberration follows parabolic curve, with the point of minimum aberration shifting along much milder curve as a function of lens position factor p (since p=1-2f/I, f being the focal length and I the final image separation, p is zero for object at 2f, when I=2f, and it is -1 for object at infinity and I=f). In effect, for given lens refractive index n, the parabola describing spherical aberration glides along the minimum aberration curve as p - i.e. relative object position vs. lens - changes, changing its position accordingly. From different angle, for any given lens shape, the aberration changes with the relative position of the object. The value of the coefficient is positive (overcorrection) for negative lens, and negative (undercorrection) for a positive lens, thus the respective plots have opposite orientation. The aberration coefficient for primary spherical is zero for p=√21, i.e. for object, or image well inside the focal point (cannot be zero for actual object and image). Thin lens' coma changes linearly with q and, unlike spherical aberration, can be zero for an actual object and image. Also, unlike spherical aberration, the coma plot has similar orientation for both, positive and negative lens, and it's identical for given n, p and q.
As object distance increases from 2f to infinity, zero point shifts from q=0 (equiconvex or equiconcave lens) to the shape closer to plano-concave/plano-convex, with the more strongly curved surface facing incoming light.
 For illustration, plots are given for the negative rear lens in a 100mm f/10 Fraunhofer dublet (blue), whose shape factor is 1.63. For this shape both spherical aberration and coma are opposite in sign and nearly equal in magnitude to that of the positive front lens (Sn vs. Sp and Cn vs.. Cp), whose shape factor is -0.25, and whose spherical aberration and coma plots nearly coincide with that for n=1.5 and p=-1. Note that since the ordinate is sf3 (spherical aberration) and cf2 (coma), the actual coefficient for the negative lens is smaller than the Sn and Cn value by a factor of |fn/fp|=1.76 raised on third and second power, respectively.

Astigmatism of a thin lens, with the coefficient given by a=n/2f, is only dependant on the lens' focal length. According to Eq. 22, the P-V wavefront error of astigmatism for a contact doublet is given  by Wa= [(1/f1)+(1/f2)](αD)2/8, with α being the field angle, f1 and f2 the front and rear lens focal length, respectively and D the aperture diameter. Since (1/f1)+(1/f2)=1/f, f being the combined doublet focal length, the P-V wavefront error of lower-order astigmatism simplifies to:

Wa=Dα2/8F      or       Wa=h2/8fF2         (95)

with h=αf being the linear height in the image plane, and α the field angle in radians. For a common 100mm f/12 doublet 1-degree off axis, it gives  Wa=0.00032, or 0.58 wave for λ=0.00055mm. With the RMS error for best focus astigmatism being smaller than the P-V error by a factor of √24, that gives the RMS wavefront error of 0.118, in units of the wavelength. This amount of astigmatism is acceptable that far off-axis, however, since the error increases in proportion to the aperture and f-ratio, it may become significant with large fast systems.

Doublet also can be affected by a specific form of chromatism at a refractive surface, resulting from the increase in spherical aberration toward non-optimized wavelengths: spherochromatism. The P-V wavefront error of spherochromatism of a contact doublet can be obtained from Eq. 48-50 (note that it is the lower-order component of spherochromatism, or primary spherochromatism; it can be accompanied with the higher-order component if higher-order spherical is significant). It can be simplified by substituting typical values for the position factor p and the shape factor q for the Fraunhofer doublet: for the front and rear lens, respectively, p1~-1, q1~0.26 and p2~2.5, q2~1.65 (p values are for the object at infinity). With this in place, the P-V wavefront error of primary spherochromatism at the best focus for a system optimized for the spectral e-line, using BK7 crown and F2 flint glass, is given as:

Ws=(s1+s2)D4/2048         (96)

with s1 and s2 being aberration coefficients for the front and rear lens, respectively, given by:

with n1, n2 and f1, f2 being the refractive indici and focal lengths of the front and rear lens, respectively. For direct calculation, the individual focal lengths can be replaced by their system focal length f relative equivalent, as f1=0.432f and f2=-0.761f. For accurate results, the radii need to be exact within a tiny fraction of mm. In practice, this level of surface radius accuracy is not necessarily met.

Eq. 96 implies that the primary spherochromatism wavefront error changes in proportion to the fourth power of the aperture, and in inverse proportion to the third power of the system focal length. Or, in proportion to the aperture size, and inverse proportion to the cube of F-number. However, same as with secondary spectrum - or spectral defocus - the energy spread caused by chromatic spherical aberration is a subject to a final "validation" by the eye and its spectral response. Both aberrations are present in an achromat, and their combined effect is cumulative, although the effect of spherochromatism remains negligibly low in long-focus systems. In order to begin to significantly contribute to the chromatic defocus error, the spherochromatism nominal wavefront error needs to become a significant fraction of the nominal wavefront error of chromatic defocus - roughly, about half as large, or larger.

Taking longitudinal aberration of the red/blue foci in an achromat to be f/2000, the P-V wavefront error of defocus is, from Eq. 51, given by D/16,000F. For a 4" f/12 achromat, that gives about 1 wave P-V error for the F/C chromatic defocus; for a 4" f/6 twice as much. At the same time, the nominal wavefront error of spherochromatism, given by Eq. 96-96.2, is ~1/20 wave P-V at f/12 and comparatively (to the chromatic defocus) still relatively insignificant with ~0.4 wave P-V at f/6. FIG. 143 illustrates the magnitude of defocus in the achromat vs. defocus and spherochromatism in an apo doublet.



FIGURE 143: Diffraction images of selected wavelengths within the visual spectrum, as they would appear if focused on with a near-monochromatic filter (patterns generated by Aberrator). Chromatism in the achromat (BK7/F2) is determined by secondary spectrum, i.e. longitudinal defocus of non-optimized wavelengths. In the apochromat (FPL53/ZKN7) it is (low) spherochromatism that determines chromatic error over most of the spectral range, with defocus reappearing toward the end of spectrum, and being dominant only in the violet (note that the non-optimized wavelengths are given in even intensity, not adjusted for eye sensitivity; their actual blurs are fainter than the e-line diffraction pattern, and end-of-range spectrum blurs are much fainter than either F or C-line blur). Below is how two different modes of correction affect intensity distribution of the polychromatic PSF (440-680nm, photopic sensitivity). Evidently, there is no appreciable change in the FWHM radius (raw resolving power), but  the area around central maxima is considerably brighter in achromats, lowering contrast in mid frequencies, and impairing resolution of close unequal doubles (note that PSFs are normalized to the peak value, since it is the relative intensity distribution that is relevant or contrast transfer).

Spherochromatism in lens objective, sometimes called tertiary spectrum, can be more serious problem with apochromats. It becomes the dominant form of chromatic aberration, increasing exponentially with the relative aperture. Apochromats, and particularly doublets, usually combine glasses with more closely matched dispersive powers than achromats; as a consequence, lens surfaces (typically the inner two radii) have to be significantly more curved in order to bring color foci together, which in turn increases higher-order spherical aberration (FIG. 144). Fast, larger apochromats can face the prospect of significant amounts of spherochromatism, both primary and of higher orders (L.A. curves of the achromat in FIG. 144 are nearly entirely secondary spectrum, i.e. defocus, while those of the apochromat, flattened for mid-zones and more strongly curved toward the edge, reveal a dominant higher-order aberration in the longer wavelengths, with lower-order spherical aberration dominant in the shorter wavelengths; for the optimized wavelength, the lower and higher-order aberration are nearly optimally balanced).

 
FIGURE 144: Secondary spectrum and spherochromatism in a 4" f/15 Fraunhofer doublet achromat (left) and a more or less typical 4" f/9.7 apochromat refractor (right). TOP LEFT: Grossly exaggerated refraction of e (green), C (red) and F (blue) spectral lines in the achromat and apochromat (the actual ray height at the last apo surface is only ~1.3mm smaller than at the front, and the blue-to-red separation at the 4th surface is little over 0.005mm). The wavelengths actually remain much tighter in the achromat's objective, but what matters is their height vs. angle when they exit the rear lens: it determines how close they focus in the image plane. RIGHT: Longitudinal (top) and transverse (bottom) aberration in the two systems. Best foci - marked by small squares - for the achromat are at 70% radius. For the blue F and red C line they are close to each other, but roughly 0.8mm - the nominal secondary spectrum - far from the optimum green focus. Longitudinal C/F spherochromatism in the achromat is approximately 0.14mm, which is ~1/50 wave P-V level. In comparison, the apochromat has its best green, red and blue foci placed much tighter in their orthogonal projection onto the axis: approximately 1/10 of the achromat's (the apo plot scale is larger by nearly four times). At the same time, its spherochromatism is greater than that of the achromat: roughly 1/10 wave P-V the red/blue average. The g violet line (436nm) in the achromat focuses more than three times farther from the e-line (to the right) than the red/blue lines. Note that best foci for lower-order spherical - characterized by the L.A. plot bending steadily to one direction toward the edge - coincides with the 70% zone focus. Higher-order spherical L.A. plot also bends in one direction, but is noticeably flatter centrally, and curving more strongly toward the edge. Best focus here coincides with ~75% zone focus. For mixed lower and higher order spherical of opposite signs, the LA plot at some point reverses and bends in the opposite direction. Best focus location for this form of aberration varies with the proportion of the two aberration forms; for a desirable, nearly balanced form (the green wavelength in the apo plot), best focus coincides with 87% and 50% zone focus. The F/C defocus in the apo is nearly 7 times smaller than in the achromat, but the error here is not defocus, rather defocused spherical aberration;
 
,

roughly, defocus equaling 1/4 of the longitudinal aberration from best focus location for spherical aberration doubles the error. If it is, as mentioned, roughly 0.1 wave for the red and blue lines in the apo, and their focus is at about 1/4 of their entire respective longitudinal aberration from best focus, the F/C error at the optimized focus is nearly 0.2 wave P-V, or only about four times less than in the achromat. However, farther wavelengths remain nearly as close in the apo as red and blue, providing much better chromatic correction in the expanded range.  BOTTOM: Strehl as a function of the wavelength for the two refractors. While the achromat has a slight edge over the wavelengths of peak eye sensitivity, chromatic correction toward both ends of the visual spectrum is dramatically superior in the apochromat. This, however, has much smaller effect on visual observing than what it appears. The reason is that eye sensitivity also dramatically decreases toward those wavelengths that are far from the achromat's best focus, effectively offsetting better part of its defocus error. Since the sensitivity plots are also normalized to 1, the effective Strehl S is approximated by 1-(1-S)E, where E is the normalized eye sensitivity for given wavelength. For instance, Strehl at the 495nm wavelength is about 0.25 (S=0.25) for the achromat, nearly equal nominally to the corresponding photopic eye sensitivity (E=0.25). Therefore, the effective Strehl is approximately  0.81. It is also higher in the apo, but the difference here is much less significant: 0.92 nominal vs. 0.98 effective visual Strehl (i.e. 6.5% contrast improvement, vs. 324% improvement in the achromat).     SPEC'S

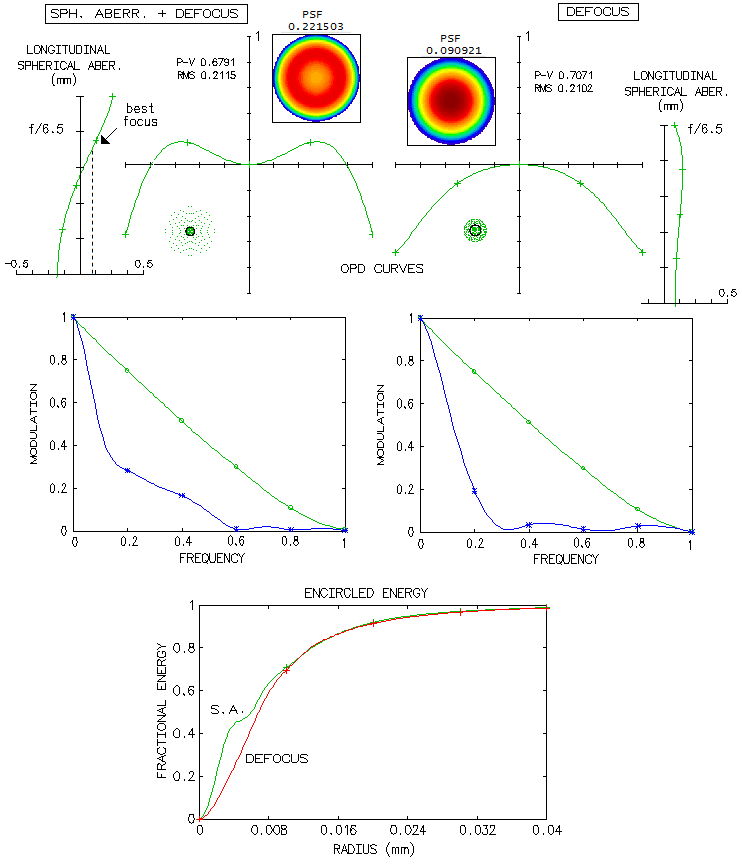
Axial chromatism, either secondary or tertiary spectrum, practically always involves two different aberrations: defocus and spherical aberration. Either can be anywhere from dominant to negligible, but they are different in their appearance and effect. For given aberration magnitude, defocus has eight times smaller longitudinal aberration, and 3.5 times smaller blur (vs. primary spherical at best focus; more vs. balanced 4th and 6th order spherical). In general, defocus is more detrimental than spherical aberration, even when the errors are nominally identical. Figure below illustrates this on the example of a f/6.5 triplet with the wavefront error in violet mainly result of spherical aberration (although defocus is not negligible) and its defocused central line with less than 0.009 wave RMS of balanced 6th/4th order spherical when in focus. The latter practically represents defocus alone, and is similar in that to the unoptimized wavelengths error in the Takahashi TOA refractors.

Despite their nominally identical RMS wavefront error, their effect on contrast transfer, as well as their Strehl ratios, are very different. Encircled energy plot explains why: diffraction image resulting from spherical aberration has smaller, well defined central maxima and still preserved ring structure, as opposed to the wider, evenly fading away defocus central maxima. That gives to the spherical aberration pattern contrast transfer advantage in the mid frequencies. This difference in intensity distribution is a consequence of their respective wavefront shapes: the inner 80% of the wavefront area (radially) has significantly smaller average deviation with spherical aberration. Hence, comparing nominal wavefront errors for non-optimized wavelengths of different lenses - i.e. standard achromats, with predominant defocus vs. doublet and triplet apos with dominant spherical aberration, done more than a few times on this site - is just that: nominal. The actual effect is likely to be smaller, possibly significantly, with spherical aberration dominant, than with defocus dominant.

The emergence of higher-order spherical aberration in apochromats is the result of more strongly curved lens surfaces; it is much more of a problem with the doublet than with triplet objectives, and the primary source of higher-order spherical in the former are the two strongly curved inner surfaces. This simply means that the 4th order surface approximation (primary spherical) is not sufficiently accurate anymore, and the 6th order surface term (secondary spherical) has to be included. This can be done by tweaking surfaces to re-introduce an optimal amount of the 4th order aberration of opposite sign, in order to minimize the total aberration. Hence, both form of the aberration are present to some degree, reshaping the wavefront into some intermediate shape. When the two are optimally balanced, which requires similar amounts of the two aberration forms of opposite sign, the higher-order aberration, as the RMS wavefront error, is reduced nearly six fold.

This changed aberration form produces different star test pattern. In general, the difference between inside and outside focus patterns is noticeably more pronounced at a given error level, possibly indicating insufficient degree of correction even if the actual error is quite small (FIG. 145). Note that the patterns are for moderately bright telescopic star (i.e. the first dark ring in aberration-free aperture is clearly visible, but noticeably fainter than central maxima); pattern appearance will change with significantly brighter or fainter stars.


FIGURE 145: Intra and extra-focal patterns for balanced higher-order spherical aberration. The discrepancy is noticeable at 4 waves of defocus already at 0.1 wave P-V (0.019 wave RMS, comparable to nearly 1/16 wave P-V of lower-order spherical). In general, one side of defocus is more contrasty, with cleanly defined concentric pattern, while the other is comparatively indistinct. As the error increase, the indistinct side of defocus is becoming noticeably brighter, developing well outlined darker central hole (for the opposite aberration sign, the in and out sides are reversed). The difference is generally more noticeable at 4 waves of defocus than at 8 (or more) waves; Only as the error nears the diffraction limit, it becomes clearly noticeable at larger defocus values. For less than perfectly balanced higher-order spherical, pattern appearance changes somewhat, becoming more similar to that for the lower-order aberration, regardless of whether the imbalance is toward dominant pure higher, or lower spherical (the two produce similar patterns), which means that the extrafocal discrepancy would tend to diminish.

    The actual lens objectives may have their higher-order spherical aberration (HSA) balanced with lower-order spherical (LSA) - or balanced higher-order spherical (BHSA) - in the optimized wavelength well below the "diffraction-limited" level, but as little as λ/50 wave RMS, is still detectable in the star test. For given P-V wavefront error, the BHSA has nearly 40% smaller RMS wavefront error than LSA. The reason is that, as shown on the inset to the left, the deformation it causes affects larger, outer wavefront area less. But, due to more strongly curved edge area, it does comparably more damage to defocused patterns. Thus, noticeably different intra- and extra- focal patterns in an apochromatic objective do not necessarily indicate compromised performance level, and it generally indicates lower error than in the case when similar apparent difference is caused by LSA alone. However, the notion that these instruments don't need to have perfect star test in order to have a perfect correction level is, of course, unfounded. The key for the proper test interpretation is in determining how well balanced are the two aberration forms. HSA alone has both, wavefront form and pattern appearance similar to that of the LSA, so the more unbalanced it is, the more alike LSA the star pattern.

In other words, damage to the pattern appearance can be significantly greater than damage to the instrument's performance. Some other telescope types, notably Maksutov-Cassegrain, also need to have this factor taken into account when interpreting defocused patterns, due to relatively significant presence of higher-order spherical aberration.


◄ 8.4.3. Off-axis Newtonian   ▐    9.1  Refracting telescope objective: Achromats ►

Home  |  Comments