9.1 REFRACTING TELESCOPE OBJECTIVE: DOUBLET ACHROMAT

PAGE HIGHLIGHTS
• Doublet achromat types • Petzval-type achromat • Effect of central line error • Effect of stopping down

As mentioned on the previous page, the idea of a doublet achromat probably comes from Chester Moore Hall in the 1730s, but it was John Dollond who had it patented in 1758 and succeeded in producing working doublet achromats. The original Dollond's doublet - possibly as the one claimed by Hall (order not specified) - had flint (negative element) in front, followed by crown, with all surfaces spherical. His son Peter modified it by putting crown in front, and correcting residual spherical aberration by aspherizing the 4th surface, polishing off its peripheral area (Dollond and Son's pursuit of achromaticity, R.Sorrenson 2001). On the other hand, there is also evidence that he was trying to minimize spherical aberration by making focal length of the central region of the crown front radius longer by removing glass from it (New Light on the Invention of the Achromatic Telescope Objective, R. Willach 1996). That would, however, be ineffective, since most of the aberration is generated on the outer lens area (in addition to the front radius generating only a small fraction of spherical aberration vs. inner radius).

From what is avalable, it seems fair to conclude that it was John Dollond who made the crucial step from the idea of combining two different glasses to actually producing lens objective with chromatism reduced to the level of an achromat (in court proceedings from 1765, Hall's doublet was described as consisting of a plano-convex crown and plano-concave flint element, with the latter having focal length three times longer; such doublet would not just have only marginally lower chromatism than a singlet lens, but would also suffer from unacceptably high spherical aberration due to a large differential between two radii). 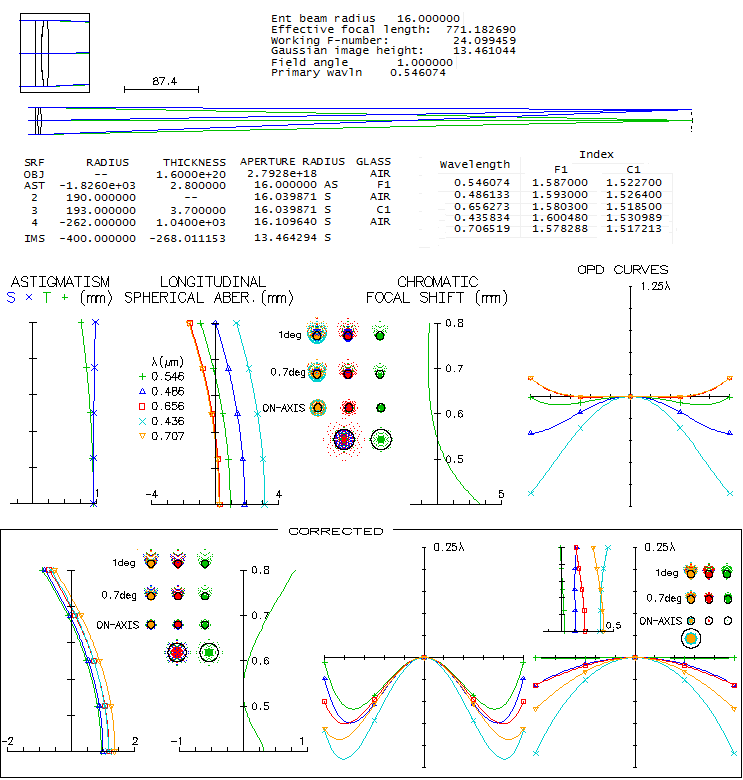Experimenting with prisms, John Dollond determined approximate value of the focal lenghts ratio for the two lenses as 3:2 (flint-to-crown), and minimized spherical aberration by making the flint element a negative meniscus, which allowed for the stronger concave radius, nearly equal to the crown element's inner radius. Below is raytrace of one of his achromats (data from Remarks to the article: New Light on the Invention of the Achromatic Telescope Objective, I. Nesterenko 2017). Note that only e, F and C-line index is measured, with the g and r values being determined by raytracing software (OSLO Edu).

It is a small 32mm f/24 lens with low residual spherical aberration. As most of the objectives from that time, it is somewhat overcorrected (vs. singlet, which has shorter wavelengths focusing closer to the objective than the longer ones). The likely reason is that it was compensating for chromatism of the 5-element terestrial eyepiece used at that time (An investigation of the eighteenth-century achromatic telescope, D.H. Jaecks 2009). Strictly talking, it is not an achromat, since no two widely separated wavelengths come to the same focus, but the level of correction is close to it. For full correction, it is necessary to make the negative element weaker (bottom box, left, R1=-3250mm). While spherical aberration is only slightly higher, significant portion of the F and C-line error comes from it. With corrected spherical aberration (R3=-211mm and, to keep F and C close together, R1=-1900mm), an optimized version of this objective (bottom right) can be compared to the modern standard achromat: 1/16 wave P-V in the F and C line, for given aperture and focal ratio, correspond to those of f/61 standard achromat, with the correction in the violet g-line (0.22 wave P-V) corresponds to that of f/89 achromat. In other words, Dollond's doublet has 2.5 times better correction in F/C, and 3.7 times better g-line correction. Some coma is present, but at this focal ratio and aperture size not noticeable (in the original configuration, 0.083 wave RMS at 1° off axis), hence Dollonds didn't need to know the calculation for minimizing it. They certainly had some knowledge about controlling spherical aberration, but judging on multiple factors - their keeping relative aperture very small, aspherizing, triplet arrangement - it was incomplete. Spherical aberration is easily controlled by balancing the two inner radii.

After that, a number of doublet types have been developed. An achromat, by definition, uses two common glasses - crown and flint - to reduce primary chromatism (chromatism of a single lens). Since chromatic correction of a doublet depends mainly on the glass combination, and common glasses span relatively narrow range of properties (i.e. refractive index and dispersion), doublets achromats have similar level of chromatism and differ mostly in their correction of monochromatic aberrations.

Typical astronomical doublet is air-spaced. Air space makes it possible to optimally correct for monochromatic aberrations with any glass combination. Cemented doublets, on the other side, require specific glass combinations that allow optimal correction with equal inner radii (for instance, BK7 and SF5; such doublets perform just as well with a small air gap). Another obstacle for cemented doublets fabrication is that in larger sizes - generally around 100mm in diameter, and larger - thermal expantion and contraction of the glass becomes detrimental for the bond between lenses.

A long time standard for doublet achromats is the Fraunhofer doublet. It is relatively easy to make, free from coma and, as any other doublet achromat, about as well corrected for secondary spectrum as a doublet made of ordinary glasses can be. The doublet consists from the positive front crown element, and negative rear flint element. The radii of lens curvature vary somewhat with the particulars of a doublet; for the standard crown and flint combination (BK7/F2) they are approximately R1~0.61f, R2~-0.35f, with the focal length of about 0.44f, and R3~-0.36f and R4~-1.48f, with the focal length of about 0.78f, R1-4 being the lens surface radii from the front to the rear, and f being the final system focal length (alternatively, the curvatures can be expressed in the inverse form, f/Ri, as c1~1.64, c2~-2.86, c3~-2.78 and c4~-0.68). This also approximates the lens element focal lengths as f1~0.43f for the crown and f2~-0.76f for the flint.

The inner two radii of the Fraunhofer can be equalized, without significant change in the correction level, on or off axis (in order to minimize ensuing spherical aberration, R4 is slightly weakened, and lens spacing slightly widened). Such modification is known as Baker doublet.

Another coma-free doublet with reversed order (flint in front) is the Steinheil, which requires significantly more strongly curved surfaces (R1~0.43f, R2~-0.224f, R3~-0.223f and R4~-f for F2/BK7 glasses).

Two other doublet achromat types of mostly historical significance are the Littrow, requiring even more strongly curved surfaces than the Steinheil, with more coma than comparable paraboloid, and the Clark, with somewhat less coma than the Littrow, but more lateral chromatism. Another older doublet type is the Cooke, which consists of the biconvex front and biconcave rear element; it has more than double the coma of Littrow, while no advantage of easier fabrication.

Diagrams below illustrate basic properties of the main achromatic doublet types: longitudinal aberration plot for five spectral lines spanning most of the visual spectrum (g-436nm, F-486nm, e-546nm, C-656nm and r-707nm), axial F-e-C ray spots, P-V wavefront error at 0.5° off-axis (e-line) and best image curvature radius.

FIGURE 146: Doublet achromat objective types for the common crown/flint combination, 100mm f/10 examples. The standard choice is Fraunhofer doublet, an aplanat consisting from biconvex front lens followed by a negative meniscus, with the secondary spectrum, defined as the longitudinal separation between the red/blue (C/F) focus and green (e-line) focus, of about 0.00055f (about 0.0005f measured from d-line). The only remaining monochromatic aberration is negligible astigmatism; best image curvature is about -0.36f (concave toward the objective). Its inverse form, with the flint element in front, known as the Steinheil, is nearly identical in performance, but requires more strongly curved lenses for given focal length. Another variation, with the inner radii equalized, and somewhat wider spacing to compensate for the spherical aberration it induced, is known as the Baker doublet and does not differ in its performance level from the other two. Unlike them, it is not strictly a contact doublet, but the air gap is relatively small. The original Littrow objective consists from the equconvex front lens followed by the negative lens of the same inner radius and flat last surface. With three identical radii and a flat surface, it is the easiest to fabricate, but at a price of some residual coma and spherical aberration. Since the astigmatism is nearly identical in all doublets and near negligible, nearly all of the 0.133 wave RMS at 0.5° off axis is coma, which makes it more than twice greater than in a comparable paraboloid (since the size of linear quality field with respect to coma changes with the third power of mirror's F-number, it makes this Littrow's coma comparable to that in a paraboloid with 30% larger f-ratio (f/7.7 for f/10 lens). Not a concern in visual observing, and neither is the residual spherical, which is here little over 1/12 wave P-V. The air gap is reduced to zero, in order to keep this residual spherical at its minimum. With larger lenses, the latter may become significant, in which case one of the two inner radii may need to be slightly changed in order to have it minimized or cancelled. Note that the last surface in the common crown/flint combination cannot be flat; it is mildly convex, since the -f1/f2=V2/V1 achromatic condition (Eq. 42) for the Littrow implies V2=(n2-1)V1/2(n1-1), where n, V and 1, 2 refer to the refractive index, Abbe number, front and rear lens, respectively, hence such lens configuration requires specific glass match (the only nearly matching flint for the flat-rear Littrow using BK7 is F15). A Littrow modification by Clark&Sons, known as Clark doublet, has the two lenses more widely separated (~15% of the focal length, according to Sidgwick), in order to make the inner surfaces accessible for cleaning without taking lenses out. Since widening the separation effectively weakens the rear relative to front lens, with the former in the Littrow already slightly too weak for cancelling spherical aberration, the Clark requires somewhat stronger (relative to R1 and R2) third surface (like the Littrow, the last surface can be flat only with a specific glass match; for the common crown/flint combinations it is mildly convex). The Clark's coma is somewhat lower than Littrow's, but its lateral color is, due to the wider lens separation, significantly larger, although still acceptable (less than 1/4 of the Airy disc diameter between F and C lines at 0.5° off axis for the above system). Also, best image surface is somewhat more strongly curved, indicating a bit stronger astigmatism: the respective Zernike coefficients for primary coma and astigmatism at 0.5° of 0.252 and 0.107 indicate 0.252/√8=0.088 and 0.107/√6= 0.044 wave RMS error, thus astigmatism about half as strong as coma, which is about a third lower than in the Littrow. Clark configuration can be coma-free with the first radius made stronger than the second one, and also stronger fourth radius. Finally, the alternative aplanatic doublet solution, consisting of a positive and negative meniscus, is the Gauss doublet. Since a meniscus requires significantly more strongly curved surfaces to achieve given power, this objective type is, in addition to be more difficult for fabrication, unsuitable for all but long focal ratio instruments. As raytrace shows, higher order spherical originating at the strongly curved surfaces - particularly R4 - makes it unacceptable already at 100mm f/10, with 0.057 wave RMS design limit in the e-line, and more than a third larger chromatic error due to spherochromatism (residual coma noticeable at the off-axis wavefront map cannot be further minimized without strengthening the radii even more, which would double the spherical error). Vice versa, accepting significantly more coma would allow for the weaker radii and reducing higher-order spherical to insignificant, but it would be still inferior to the other doublets, both, for more difficult fabrication and lower field quality. The positive is somewhat lower astigmatism - about 1/3 of the Clark objective, and nearly half of the other doublets' - and correspondingly less strongly curved best image surface.

Following table gives design specifics for doublets achromats consisting of BK7 crown and F2 flint, with all measures in units of the focal length. The specs are based on 100mm f/10 objectives, but are scalable within the normal range of refractor apertures, up to about 50% faster or any slower objective (by applying the desired focal number ratio to 10 directly to the radii), with only minor raytrace adjustments. Substituting similar glasses should also require only minor adjustments; glass thickness is generally not a significant factor, the exception being the Gauss objective.

TABLE 11: ACHROMAT DOUBLETS: GENERAL SPECIFICATIONS FOR BK7/F2 GLASS (in units of focal length)
Type	aplanat	R1	t1	M1	R2	AIR (M2)	R3	t3	M3	R4
FRAUNHOFER	YES	0.6	0.011	BK7	-0.36	0.001	-0.363	0.007	F2	-1.51
STEINHEIL	YES	0.442	0.007	F2	0.229	0.001	0.2285	0.009	BK7	-15
BAKER	YES	0.582	0.011	BK7	-0.363	0.003	-0.363	0.007	F2	-1.59
LITTROW	NO	0.45	0.01	BK7	-0.45	0.00005	-0.45	0.006	F2	-7.7
CLARK	NO	0.428	0.01	BK7	-0.428	0.015	-0.4	0.0065	F2	-8
GAUSS (~f/14 and slower)	YES	0.129	0.00665	BK7	0.3345	0.0003	0.14206	0.0042	F2	0.10357
COOKE	NO	0.373	0.009	BK7	-0.563	0.001	-0.527	0.006	F2	4.7

A doublet with air gap wide as Clark's can be made aplanatic, in which case it is jus another variant of the Baker, with the third radius somewhat more strongly curved.

Relatively unusual achromat designs are triplet achromats, as well as those with more than one group of lenses. The latter include Petzval-type achromats and those with the second lens group closer to the focal plane. By their basic form, they belong to dialyte objectives, defined as those employing widely separated elements.

Triplet achromats require more glass and work, but offer no significantly better correction of aberrations - either monochromatic or chromatic - than doublet achromat. The only possibly beneficial use of the triplet would be for very fast, large achromats with significant level of higher-order spherical aberration.

Petzval-type achromat is a design that uses two groups of lenses, with the rear group at 1/3 to 2/3 of the focal length of the front group behind (approximately; in the original Petzval configuration rear doublet is at half the focal length of the front doublet apart, its focal length half that of the front doublet, and the combined f.l. also half that of the front doublet). If using common crown and flint glasses, such arrangement can reduce secondary spectrum by approximately 15%; apparently, generally not considered worth the extra expense. With the second lens group closer to the focus of the front group, which is not Petzval configuration, rather one with sub-aperture corrector, secondary spectrum can be reduced somewhat more, up to about 30%.

The reason for this is that the blue and red exit the front lens group - which is assumed to be doublet achromat - only slightly separated, but at different angles: as FIG. 96 hints, the red just below, and blue just above the green ray, with the former two converging to a common focus (or nearly so) and emerging above the green ray at some distance toward the focus. Thus there is no appreciable effect on longitudinal chromatism by the second group of lens, until it is far back enough for the red/blue rays to raise above the green ray, and get refracted more strongly at the rear lens group, focusing slightly shorter relative to the green light.

Additional advantage of the dialyte form in an achromat is that astigmatism can be manipulated, either cancelled for less curved image field, or added in the opposite sign, still very low, in order to flatten the field, as illustrated below (FIG. 147C).

FIGURE 147: Standard Fraunhofer doublet achromat can be combined with an auxiliary widely separated second doublet for enhanced correction (A) 100mm f/10 objective alone, for comparison (B) Petzval-type achromat with a cemented rear doublet. The front lens is an f/10 doublet. The only significant change is that the front doublet is bent to generate coma cancelling the coma of rear doublet, which in turn cancels out astigmatism. As a result field curvature equals the focal length, and there is no other monochromatic aberrations to speak of. Since the astigmatism is cancelled, best image surface coincides with the Petzval surface. (C) Another f/10 doublet in front, with a doublet sub-aperture (field) air spaced corrector. Again, the main modification is bending the front doublet to induce some coma, offsetting that of the corrector which, in turn, flattens the field w/o introducing significant astigmatism. In fact, astigmatism is lower than in a comparable achromat (D). Chromatism is also lower in both double achromats (somewhat more in the one with field corrector), without appreciably larger lateral color (note that the Airy disc for
e-line spot at 0.5° off-axis is enlarged for clarity).

As the examples above indicate, required change of the basic (front) doublet achromat in an optimized 2-doublet arrangement are relatively small. It mostly limits to bending the lenses to obtain either flat field or cancel astigmatism. Its chromatic correction can remain unchanged (infinity-corrected) if the rear achromat's is set for its object distance (which is, effectively, equal to the separation between rear doublet and virtual image formed by the front doublet). The former generally needs to be somewhat overcorrected in the blue (i.e. with blue and green having nearly a common focus, and the red focusing farther away), as well as somewhat overcorrected spherical-aberration-wise vs. doublet corrected for infinity (unless the front doublet induces offsetting aberrations).

Use of special glasses for the rear corrector does not appreciably improves chromatic correction of such systems, because it is already being generated by the front doublet. For significantly improved chromatic correction, rear doublet has to be designed so that it offsets the chromatism induced by the front doublet, which requires complex lens systems. Alternately, both doublets have to be made with special glasses.

A system with apochromatic correction can be made with common crown and flint, but such system would require three groups of lenses (two separated doublets and a positive lens closer to the focal plane for lateral color correction), and would be significantly longer than the effective focal length. It would also require strongly curved surfaces, generating significant higher order spherical aberration.

Use of special low-dispersion glasses in combination with common glass types makes possible much higher level of chromatic correction in a doublet, triplet or Petzval refractor. The degree of improvement is determined by the respective properties of the two glasses combined, and can vary significantly. Somewhat informally, such refracting objectives are referred to as semi-apo and apochromatic (apo). Following page gives several examples, including some that were, or still are marketed, but before that a quick look on the effects of central line error and stopping down an achromat.

EFFECT OF THE CENTRAL LINE ERROR ON CHROMATIC CORRECTION

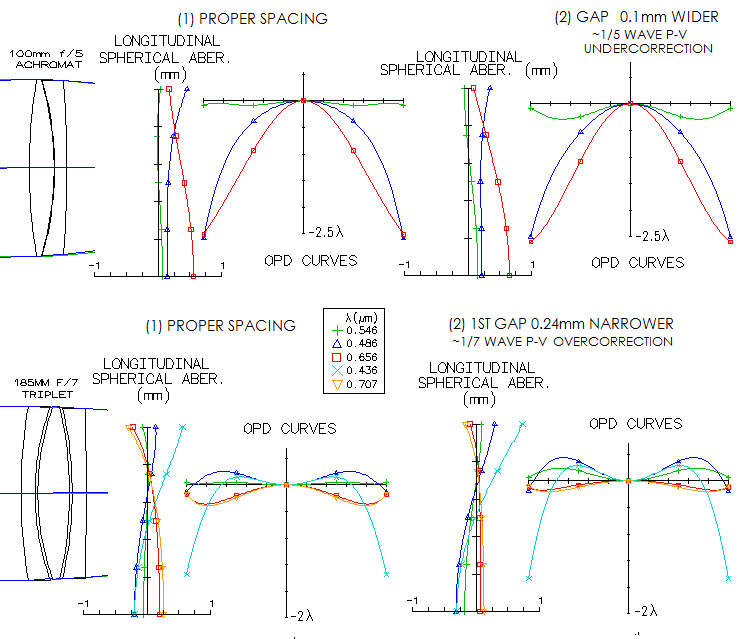
Presence of spherical aberration in the central line means that it is inevitably carries over to all others. Since spherical aberration in the red and blue are usually of opposite sign at the minimized central line error, any induced sphrical aberration (from miscollimation, or radius error) will add to one, and subtract from the other one. In general, spherochromatism in achromats is low, dominated by chromatic defocus, hence a small to moderate central line error will not significantly affect their chromatic correction. As raytrace below shows, that is the case with as fast as a 100mm f/5 unit (top).

1/5 wave P-V of spherical aberration only slightly increased P-V error in the red, and have it slightly reduced in the blue. However, in a correction mode with colors tightly bound together - i.e. apochromatic correction - the effect can be significant. As little as 1/7 wave of overcorrection in a triplet shown (Ascar 185mm f/7) caused the error in the central line to exceede error in the red C line, which has the error reduced, while also appreciably increasing the blue and violet error.

EFFECT OF STOPPING DOWN ACHROMAT

Stoping down achromat generally reduces all its aberrations, but it will likely cause chromatic disbalance which may not be significant, but could be noticeable vs. achromat unit with the same aperture and focal ratio that has the colors optimally balanced.

The longitudinal aberration plot shows that the color curves are being literally trimmed off at the mask radius level. Despite no change in the respective paraxial foci location, that effectively pulled the blue closer to the green focus, while pushing the red farther out. As the OPD plots show, the error is significantly reduced in both, F and C line, due to the larger Airy disc and decreased defocus sensitivity, but significantly more in the former. Spherical aberration is also significantly smaller. It is of no practical consequence in this case, with it being negligible at a full aperture, but can be significant if the error at full aperture is not negligible. For primary spherical aberration, the wavefront error changes in proportion to the 4th power of the aperture, but in fast achromats with a mix of lower and higher order SA, reduction factor will vary somewhat; in general, it is smaller.

◄ 9. REFRACTING TELESCOPES ▐ 9.2. Refracting telescope objectives: Apo and semi-apo ►

Home | Comments