|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
4.7.1. Secondary
spectrum and spherochromatism
Secondary spectrum
Fortunately, chromatic aberration of a
single lens - primary spectrum - can be
significantly reduced with a pair of lenses combined. Defining
"achromatic" as the level of correction where both longitudinal and
lateral chromatism are cancelled for two wavelengths near the opposite
ends of the visual range, a lens pair - or "doublet" - is
achromatic if
the individual lens focal lengths are the reciprocal of their
Abbe numbers:

with f1,2
being the lens focal lengths (given by
Eq. 1.1.) in the e-line, and V1,2
their respective Abbe numbers (dispersion), with the subscripts 1
and 2 referring to the front and rear lens, respectively. The equation implies that
the two lenses need to have opposite powers, and that the weaker lens
(normally, the negative element of a telescope objective) needs to have
proportionally stronger dispersion in order to offset chromatism induced
by the stronger lens.
For near-contact or contact
pairs, the system focal length f relates to the focal lengths of
individual lenses f1
and f2
as 1/f=(1/f1)+(1/f2).
This determines the individual lens' focal lengths in terms of the system
focal length and Abbe numbers as:
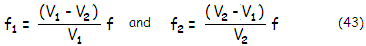
If we choose to cancel
chromatism for the F (486nm blue) and C (656 nm red) lines, then the curvatures of the front and
rear lens need to relate as:
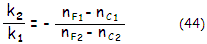
with k=(1/R1)-(1/R2),
where R1,2
is the front and rear lens radius of curvature, respectively,
and
nF1,
nC1
and
nF2,
nC2
refractive indici of the selected distant wavelengths for the front and
rear lens, respectively. This relation tells that for bringing F
and C to a common focus, the magnitude of dispersive powers of
two glasses in F and C for two glasses needs to relate as
the inverse of their optical power (since the curvature k is directly
proportional to the optical power). For instance, if the positive
element in a doublet has 50% greater optical power than the negative
element, its dispersive differential between F and C has
to be as much smaller.
In other words, secondary spectrum of a doublet
does not depend on the lens shape, only lens power. This
leaves enough room for lens "bending", so that other (monochromatic)
aberrations are also corrected or minimized.
But bringing two widely
separated wavelengths to a common focus does not make all the
wavelengths over the visual range nearly parfocal. Those in between will
still focus shorter, and those closer to the range ends will focus
longer. This form of residual chromatic defocus is called
secondary spectrum.
 Graph
at left shows secondary spectrum of a 100mm aperture f/10 doublet
achromat with a common crown/flint combination (BK7/F2). With F
and C line focusing close together, the shortest focus is around
the e-line, with all other wavelengths focusing longer. If the
longitudinal foci of individual wavelengths are projected onto a
vertical wavelength scale, they form a parabolic curve (dashed) which
represents focal (chromatic) shift vs. wavelength. As graph shows, all
other wavelengths also form common focus, with every wavelength toward
the blue end having its counterpart toward red. Height of the
parabola's tip (and its shape, slightly) changes with the particular mode of correction. The standard
mode brings together F and C foci, because at the time of
early achromats it was believed that eye sensitivity for these two lines
are similar, and bordering significant. In fact, the blue is more
significant even in photopic (bright light) conditions, and more so
toward lower light conditions, typical of those during observing. Hence
the optimum correction for general observing would bring together F
and a wavelength somewhat shorter than C, tilting the parabola
somewhat Graph
at left shows secondary spectrum of a 100mm aperture f/10 doublet
achromat with a common crown/flint combination (BK7/F2). With F
and C line focusing close together, the shortest focus is around
the e-line, with all other wavelengths focusing longer. If the
longitudinal foci of individual wavelengths are projected onto a
vertical wavelength scale, they form a parabolic curve (dashed) which
represents focal (chromatic) shift vs. wavelength. As graph shows, all
other wavelengths also form common focus, with every wavelength toward
the blue end having its counterpart toward red. Height of the
parabola's tip (and its shape, slightly) changes with the particular mode of correction. The standard
mode brings together F and C foci, because at the time of
early achromats it was believed that eye sensitivity for these two lines
are similar, and bordering significant. In fact, the blue is more
significant even in photopic (bright light) conditions, and more so
toward lower light conditions, typical of those during observing. Hence
the optimum correction for general observing would bring together F
and a wavelength somewhat shorter than C, tilting the parabola
somewhat
Since only a single point on axis - paraxial focus, formed by paraxial
(central) rays - represents
a wavelength here, this graph does not show spherical aberration - i.e.
change in longitudinal focus location with the zonal height - present
in
each wavelength (spherochromatism). For that, chromatic defocus
needs to be shown vs. zonal height in the pupil (inset top left); for
instance, marginal focus for the violet h line is about 0.75mm
longer than its paraxial focus, with the corresponding P-V error of
spherochromatism at the best focus (0.707 zone focus location for
primary spherical aberration) given by 0.75/64F2=0.0001172mm,
or 0.29λ
for
λ=0.000405mm wavelength. For
near-equal wavefront error, the common F/C focus is close to the
marginal rays foci of these two wavelengths, with the paraxial foci somewhat separated,
as indicated by the focal shift plot.
In order for a doublet to have identical focal
length for an additional, third wavelength in the
mid-range (e-line here),
it also needs to satisfy the relation:
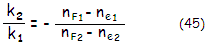
which, considering Eq. 44, implies the equality:
(nF1-ne1)/(nF1-nC1)=(nF2-ne2)/(nF2-nC2)
(45.1)
i.e. that the value of the ratio of dispersive differential between F
and e vs. that in F and C needs to be identical for
the two glasses in order to have these three wavelengths brought to a
common focus.
The
(nF
-ne)/(nF
-nC)
factor is called
relative partial
dispersion (RPD) of glass for these three wavelengths, hereafter denoted PF,e.
General formula for the relative partial dispersion is Px,y=(nx-ny)/(nF-nC).
It determines the magnitude of separation between the common F/C
paraxial focus, and paraxial focus of the wavelength x, as:
Δf = [P(x,y)2-P(x,y)2]f/(V1-V2)
= (ΔP/ΔV)f
where Δf is the
secondary
spectrum,
f is the objective focal length, subscripts 1 and
2 denote the two glasses, and ΔP and ΔV are the RPD
and Abbe number differential for the glasses, respectively. As the
relation implies, two glasses of equal RPD for given three wavelengths
will have zero focus differential for those wavelengths - i.e. will
bring them to a common focus - while with non-zero RPD differential the
magnitude of defocus between the wavelength x and common F/C
focus, as a fraction of the wavelength, is proportional to the ratio ΔP/ΔV.
Hence, two glasses with equal PF,e
values will bring F, C and e spectral lines to a
common focus. What is commonly referred to as secondary spectrum is the
Δf value for these three
wavelengths, i.e. the e-line focus vs. common F/C focus separation;
however, it could also be any other wavelength vs. F/C focus. For
instance, using Pg,F
and corresponding wavelengths will indicate separation between the
violet g-line and common F/C focus.
One should keep in mind that this is strictly valid
for the paraxial foci. When spherical aberration in non-optimized
wavelengths (spherochromatism) is significant, their best focus shifts
significantly away from their paraxial focus, which to a smaller or
larger extent makes the actual chromatism differ from one based on the
paraxial foci.
Thus doublet satisfying Eq. 42-45
brings two widely separated wavelengths
and a third, mid-wavelength, to a common focus. Practically, assuming
negligible spherochromatism, it means that
all other wavelengths within this range are also nearly parfocal. Such
doublet is called apochromatic. Thus, apochromatic
objective corrects for both, primary
and secondary color error. That alone still doesn't guarantee
high-level correction of chromatism, since spherochromatism in lens
objectives with strongly curved surfaces can be significant. This is why
Abbe's apochromatic condition, in addition to practically eliminating
secondary spectrum, requires good correction of spherical
aberration across the wavelength range (tertiary
spectrum) as well, with the most stringent (not specified,
though) requirement being for the optimized wavelength.
When only achromatic condition (Eq. 44) is satisfied, two widely
separated wavelengths come to a common focus, with the the longitudinal
focus deviation for the wavelengths between them increasing relatively
slowly toward approximately the mid-wavelength - green e-line focus for
the common F/C focus - and much faster toward external wavelengths, more
so toward blue/violet than red. Longitudinal focus deviation of these
other wavelengths vs. common focus is called secondary spectrum.
It is commonly expressed as the longitudinal separation between the
common-focus wavelengths (blue/red) and shortest-focus (green) focal length,
with the latter being the mid-wavelength with the maximum defocus
relative to the common focus. For the canonical F/C common focus, the
farthest-focusing mid-wavelength focus is (approximately) that for the
e-line. Since, according to
Eq. 1.2-1.2.1 their
respective focal lengths can be written as:
1/fFC=(nF1-1)k1+(nF2-1)k2,
and
1/fe=(ne1-1)k1+(ne2-1)k2,
the differential, or F/C-e secondary spectrum, is
1/fFC-1/fe=Δ/f=(nF1-ne1)k1+(nF2-ne2)k2
(45.2) Obviously, we can have secondary
spectrum cancelled by making k2/k1=(nF1-ne1)/(nF2-ne2),
but we cannot do it unless we already have fulfilled k2/k1=(nF1-nC1)/(nF2-nC2),
which is the condition for the primary goal of bringing two wavelengths
near the opposite ends of visual spectrum to a common focus. Without it,
it would mean simply bringing F and e lines, alone, to a
common focus. It is good to make distinction between the terms
shortest-focus and optimized wavelength, since the two may
and may not be the same. As mentioned, the former refers to the mid
wavelength with the maximum longitudinal separation from the common
focus of two widely separated wavelengths. The latter refers to the
wavelength with minimized spherical aberration (since only a single
wavelength can have it cancelled). Graphically, the former is the
wavelength with paraxial focus at the largest longitudinal separation
from the paraxial common focus (FIG. 67 bottom), i.e. the one at the
tip of the chromatic focal shift plot. For the canonical
F/C common focus, the shortest-focusing wavelength is approximately the
e-line. On the other hand, optimized wavelength is the one with nearly
straight longitudinal zonal plot (e-line on FIG. 67 top), regardless on its
position on the chromatic focal shift plot. By a slight adjustment in one
of the inner radii and/or separation, any wavelength can be optimized to
near-zero spherical aberration.
If, for instance, the canonical F/C common focus
achromat is overcorrected in the e-line - i.e. has this line curving to the
right on the longitudinal aberration plot - optimized wavelength is
shifted toward the red end, to the wavelength which is somewhat less
than 1/4 wave undercorrected (inversely proportional to the wavelength)
when the e-line is, as it should be, the one with the minimum spherical
aberration, while the error of overcorrection is added (again, at a
somewhat larger scale, increasing in proportion to the wavelength)
toward the blue/violet end. This directly implies that
for all but one wavelength,
there is an inherent axial error in an achromat, and that is spherical aberration
(spherochromatism), increasing away from the optimized wavelength; at
any wavelength, defocus error exists
only relative to some other wavelength, and
can be cancelled by refocusing.
The respective
curvatures of the two lens elements k1=(1/R1)-(1/R2)
and k2=(1/R3)-(1/R4),
can be expressed as k1=1/(nF1-nC1)(V1-V2)f
and k2=1/(nF2-nC2)(V2-V1)f.
After substitution, axial separation between the red/blue (F/C) focus and the
e-line focus - the secondary spectrum - is given by:
 For the
canonical achromat with the common C/F focus and the shortest e-line focus (so called C-e-F correction), using BK7/F3 glasses for the
front and rear lens, respectively, this gives longitudinal chromatic
error (as the separation of the green focus from the common blue/red focus,
a standard measure of secondary spectrum) as:
Δf
= - (3.348732 - 4.5799n1
+ 2.230453n2)f (46.1)
with
n1
and n2
being the indici of refraction for the chosen wavelength for the front
and rear lens, respectively, and f the system focal
length (since P(F,e)1<P(F,e)2,
secondary spectrum is numerically negative, because it is measured from
the common F/C focus, which is farther away from the objective, to the
right).
Substituting indici for the e-line (n1=1.51872,
n2=1.61685
for BK7/F3 doublet)
in the above relation gives Δf=-0.000546f,
or -f/1832 as the separation between the green (e-line) and red/blue
focus (the minus sign indicating that the latter is farther away from
the objective). When measured from d-line focus, which is closer to the
common F/C focus, secondary spectrum is slightly better than f/2000; the
difference is, of course, only numerical, since the level of chromatic
correction doesn't change.
Alternately, since the plot of chromatic defocus vs. shortest-focus
wavelength within the visual range (0.4-0.7μm) nearly conforms to a
parabola, nearly identical in shape and coordinates for the common
achromat glass pairs, secondary spectrum in this range, as the defocus
relative to the focus of the wavelength's that has the shortest focus
(tip of the parabola),
can be closely approximated by a parabolic formula of the form:
y = x2/(2x-0.5)
(47)
where y is the defocus measured from the tip of parabola (the
shortest-focus wavelength), and x=λ0-λA
is the wavelength differential in microns between the shortest-focus (λ0)
and arbitrary (λA)
wavelength.
Thus, any two different wavelengths λ1
and λ2
with non-zero wavelength differential vs. shortest-focus (zero x)
wavelength will have their respective defocus relative to the
zero-defocus wavelength (tip of parabola) relating as:
y1/y2=(2x2-0.5)x12/(2x1-0.5)x22.
Knowing that the actual defocus for the F/C lines vs. zero-defocus e-line
wavelength (reversed secondary spectrum) in the standard achromat is yF,C= ΔfF,C=f/1850,
f being the focal length,
and their respective wavelength differential in microns are -0.06 and
0.11, substituting these into (y1/y2)ΔfF,C
gives the defocus ΔfA
for an arbitrary wavelength within the visual range as:
ΔfA
= [106xA2/(2xA-0.5)]ΔfF,C
for the (numerically positive) wavelength differential xA
toward blue/violet, and
ΔfA
= [60xA2/(2xA-0.5)]ΔfF,C
for the (numerically negative) wavelength differential xA
toward red.
From the nominal defocus ΔfA
it is easy to obtain the corresponding P-V defocus wavefront error from
W=ΔfA/8F2,
F being the objective's focal ratio. For
ΔfA
in mm, the wavefront error in units of the wavelength λ is
Ww=ΔfA/8λF2,
with λ also in mm. Obviously, when F and C line
foci coincide, the shorter wavelength will have (assuming negligible
spherochromatism, i.e. pure defocus error), proportionally larger
wavefront error.
Although nearly coinciding F and C-line focus is canonically assumed, this is not the best
chromatic correction mode, since eye sensitivity in the F-line is more than twice
that in the C-line even in photopic mode (bright light conditions), and
still increasing significantly toward scotopic (dim light conditions) mode.
Thus better correction mode is with the wavefront error in F and
C nearly equalized, or even somewhat smaller in the blue line.
The significance of the difference between these two modes increases
with achromat's relative aperture (FIG.
67).

FIG. 67: Longitudinal zonal aberration for F, e and C
lines (top) and chromatic shift plot (bottom) for the canonical
common-F/C-focus and equal wavefront error (WFE) correction mode.
TOP: Each outlined plot
shows the canonical secondary spectrum mode, with the paraxial F/C foci
coinciding. However, better chromatic correction is achieved with the
wavefront error in F and C nearly equalized, due to the
lower error in the blue/violet. In
a 100mm f/10 achromat, due to the
presence of spherochromatism, the wavefront errors in F and C
are nearly equalized when their marginal rays nearly coincide, with the
blue paraxial focus closer to the green focus, with the C
paraxial focus nearly twice farther away than that in F; in a 100mm
f/5,
approximately when 0.8
zone foci in F and C nearly coincide, with the C
paraxial focus about five times farther away from the paraxial e-line
focus than the F focus,
and in a 100mm f/15 when F and
C focusing segments are separated, with the paraxial C
focus about 50% farther away from the green than the blue F
focus. Dashed horizontal line indicates the location of best
(diffraction) focus, with the wavelengths focusing at it being at the
intersection with the chromatic shift parabola. BOTTOM: Chromatic shift plots corresponding to the
longitudinal zonal aberration plots above show the effect of switching from
the canonical common F/C focus to the generally better equal F/C WFE as a
shift of the plot to the left, toward shorter wavelengths (expected,
since it results in lowering the error in the F line, and
increasing it in the red). The shift is approximated with 248/F3/2
in nanometers, or 0.25/F3/2
in microns. Since the rate of change with any given
sideways shift of the plot is significantly higher at its raised
(blue/violet) end, switching to the equal F/C WFE mode results in a
better overall chromatic correction; the gain is most significant at
f/5,
with the polychromatic Strehl (430-670nm, photopic) SP
increasing from 0.53 to 0.63, still appreciable at
f/10 (0.79 vs.
0.76), and negligible at f/15.
The new common focus shifts from F and C to somewhat
shorter wavelengths (intersect of the black curve and dotted gray).
Obviously, this plot shift to the left also results in the
shortest-focus wavelength shift toward shorter wavelengths. It is
negligible at
f/15 and
f/10, but at
f/5 it
can be significant: here, the plot also sinks slightly below the zero
line, which means that some shorter wavelengths now focus shorter than
the e-line (the apparent plot sag is due to the selected primary
wavelength in raytrace being e-line, with respect to which is the
horizontal line drawn). Specifically, the shortest focus is in the 524nm
wavelength, bending back toward 506nm, where it coincides with
the optimized e-line focus (however, since spherical aberration can be
corrected only in a single wavelength, there is as much as 1/4 wave p-v
at 506nm's best focus, and four times as much at its paraxial focus, nearly
coinciding with the best e-line focus). The best diffraction focus is
shifted somewhat from e-line toward the common blue/red focus (dashed). Note
that the focal shift scale for the three f-ratios is not uniform.
These plots imply that chromatic error in an achromat with given glass
combination and optical quality (including spherical aberration level)
will vary somewhat with its secondary spectrum mode; the faster
objective, the more so.
The defocus value for the equal F/C error mode can be approximated using
the same expression as for the common F/C focus mode, only with the
wavelength differential xA
replaced by (xA-0.25/F3/2),
keeping in mind that xA
is positive for the wavelengths shorter than e-line, and negative for
the longer ones.
Following table shows numerical values of axial defocus (secondary spectrum) and
corresponding P-V wavefront error in two actual objectives, for the five common spectral lines
spanning the visual range (note that the wavefront error is a subject of
both, longitudinal defocus and spherical aberration).
| 100mm f/10
BK7/F2 ACHROMAT |
PARAXIAL DEFOCUS (P-V WFE) |
SP |
h
405 |
g
436 |
F
486 |
e
546 |
C
656 |
r
707 |
| paraxial F/C foci coinciding |
Δf |
5.45 |
2.7 |
0.55 |
0 |
0.55 |
1.1 |
0.76 |
| Ww |
14.8 |
7 |
1.62 |
0 |
0.88 |
1.73 |
| near-equal wavefront error |
Δf |
4.06 |
1.93 |
0.41 |
0 |
0.75 |
1.36 |
0.79 |
| Ww |
13 |
5.9 |
1.2 |
0 |
1.2 |
2.1 |
The near-equal F/C wavefront error secondary spectrum mode does not
strictly define the best mode of chromatic correction. According to
raytrace, polychromatic Strehl for photopic eye is at its maximum for
the error in F nearly 20% smaller than in C, i.e. with
their respective paraxial foci somewhat more separated. However,
considering eye's shift toward mesopic mode in the typical observing
session, the F error - and that in the blue-violet end in general
- should be still smaller relative to the C error, more so in
observing relatively dim objects.
Note that this assumes no appreciable spherochromatism; even moderate
level of spherical aberration in any given wavelength spreads its focus
over a longitudinal segment, with the best focus location shifted away
from the Gaussian (paraxial) focus, which is the basis of measurement
for the secondary spectrum. Moderate spherochromatism can either
somewhat reduce, or increase the actual chromatic error (defocus and
spherical aberration combined); significant amounts are generally
undesirable.
Although a term secondary spectrum
generally applies to all wavelengths deviating from the common red/blue
focus, it is most often used to designate the above focal separation,
i.e. that between the common blue/red focus and focus of the
shortest-focus (green) wavelength, normally also optimized for the
minimum spherical aberration. Since the defocus for other
wavelengths is nearly proportional to the F/C-to-e separation, it is a
measure of the magnitude of secondary spectrum. The limit to
chromatic correction for doublet achromat made with common glasses,
expressed as the red/blue-to-green focal separation is somewhat smaller
than f/1800 if measured as F/C-to-e-line foci separation, and ~f/2000
when measured as F/C-to-d-line foci separation. Centered on
e-line, defocus increases exponentially
(with the square of wavelength differential) toward
either end of the spectrum
(FIG. 68).

FIGURE 68: LEFT: Secondary spectrum
in a 100mm
f/10 doublet achromat. Canonical doublet achromat brings blue F-line
and red C-line focus close together, with the shortest-focus being
that of the green e-line (C-F correction). Spherical aberration
is canceled at the e-line. Since C- and F-line are brought to
a common focus, their axial separation from the e-line focus (focal
shift) is
near-identical, an so are their respective blurs (which, considering
smaller Airy disc at the shorter wavelength, implies somewhat larger
wavefront error in the blue).
Defocus aberration worsens much more rapidly toward the blue end of
the spectrum. This is even
more pronounced in C-e corrected achromats, where C- and
e-line
are brought to the common focus, with the shortest focus shifting
closer to the d-line, and
with reduced defocus error in the red. However, the blue/violet
end is practically sacrificed, fading away into much more quickly
expanding chromatic defocus. The downside is not only in losing the
blue/violet end, but also in compromising a portion of the green
toward the blue. Considering eye sensitivity curves for
bright (photopic)
and dim (scotopic)
light conditions, correction
shifted toward the blue end
(d-F) offers best overall visual performance.
As mentioned before, these standard chromatic shift plots show the paraxial
focus shift, hence they don't show the common foci on the same
horizontal line (it is the best foci of these respective lines that
are near each other, i.e. approximately at the same horizontal line).
Note that the small differences in the height of the tip of parabola
are due to raytrace placing zero at the default wavelength, in this
case the
e-line.
RIGHT: Proper
combination of two glasses of different dispersions not only greatly
reduces longitudinal chromatism, it also changes the form of
aberration. While that in a single lens (primary chromatism)
has shorter wavelengths focusing shorter, and longer wavelengths
longer, the combined lens - an achromat - has all wavelengths but
one in the mid-range focusing farther away. Similarly to the singlet, the
rate of defocus increase with the wavelength differential is
significantly higher toward shorter wavelengths. However, while
defocus error increase with wavelength differential is closer to the linear
in the singlet, in the achromat it changes exponentially (averaged over
blue/violet and orange/red, with the square of wavelength
differential but, as the graph shows, significantly faster in the
former), effectively forming a parabola tilted toward the
longer wavelengths. Consequently, when the defocus error of a
singlet in F and C is at the similar level to that in a doublet
(100m
f/170 singlet vs. 100mm
f/12 achromat above), the former still
has significantly more chromatism (0.55 vs. 0.80 polychromatic
visual Strehl), due to its error in all the wavelengths between F
and C, except the e-line, being larger. A singlet needs to have the
F/C error nearly half that of the achromat (100mm
f/340 vs. 100mm
f/12 achromat) in order to reach its chromatism level.
Since the sum of the relative partial
dispersions for an apohromatic doublet is, by definition, effectively zero, so is
its secondary spectrum. In reality, there is always some residual
secondary spectrum, but it is entirely negligible with well designed and
made objectives.
Since it is the combination of optical
power and dispersion properties of two glasses that determines degree of
chromatic defocus, it can't be significantly improved by adding more
lens elements of identical or similar glass types. Triplet objective
makes it easier to have better overall correction of aberrations, but
will not have appreciably lower secondary spectrum than a doublet made
of the same two glass types. The most significant advantage of a triplet
objective is that it allows for significantly weaker lens surfaces and,
consequently, greatly reduces spherochromatism. That makes it objective
type of choice for well corrected faster/larger refracting objectives.
In addition, if instead of a single common glass type it uses two
different ones, neither has to have near-zero relative partial
dispersion (RPD) differential vs. low-dispersion element, as long as
their respective RPD are opposite in sign, and nearly offsetting one
another. That widens the number of possible glass combinations available
for a triplet vs. doublet, making finding the glasses easier.
Spherochromatism
Unlike the magnitude of secondary spectrum, which can be quickly found
from the RPD differential, or estimated just from looking at the
RPD plot,
chromatic spherical aberration or, spherochromatism
(tertiary spectrum), is more difficult to anticipate. It changes
not only with the refractive index (wavelength) but also with both,
surface curvature and lens shape, requiring more extensive calculation.
More so because its higher-order form (secondary
spherical) can be significant, particularly in relatively fast
apochromatic doublets.
As mentioned, lower-order (primary) spherical aberration can't be
made zero in a single lens, but can be cancelled in a doublet. However, it
can be cancelled only for a single wavelength. Others wavelength will be
uncorrected, the farther away from the optimum wavelength, the more so.
From Eq. 7, the wavefront error of
primary spherical aberration
of a thin lens contact doublet at the best (diffraction) focus can be expressed as:
W = (S1+S2)(ρ4-ρ2)
(48)with
S1
and S2
being the peak aberration coefficients of the front and rear lens,
respectively, and ρ
the ray height in the pupil (aperture) in units of the radius. The peak
aberration coefficients are S1=s1d4
and S2=s2d4,
with s1
and s2
being aberration coefficients for the front and rear lens, respectively,
and d
the pupil (aperture) radius. General expression for the aberration
coefficient of spherical aberration of a thin lens is:
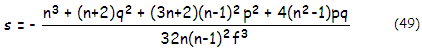
with n being the
refractive index, q=(R2+R1)/(R2-R1)
the lens shape factor, and p=1-(2f/i) the lens position
factor (FIG. 69), with f
being the lens focal length, and i the lens-to-image
separation.
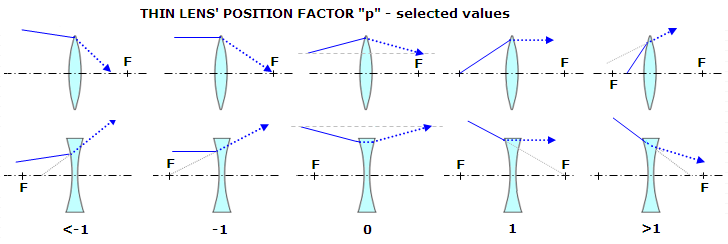 FIGURE 69: Position factor p of a thin lens
changes with the lens type (positive/negative) and the properties of
light cone incident to it, with respect to lens' focal point
F and the resulting image
separation i, as given by
p=1-2f/i.
FIGURE 69: Position factor p of a thin lens
changes with the lens type (positive/negative) and the properties of
light cone incident to it, with respect to lens' focal point
F and the resulting image
separation i, as given by
p=1-2f/i.
For the front lens the object is at infinity, so i1=f1
and p1=-1,
resulting in:
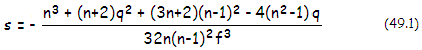
For
the rear lens, the final image separation equals doublet's focal length, thus i2=fd
and p2=1-(2f2/fd),
with
f2
being the rear lens focal length, and fd
the doublet focal length. The thin lens' focal length f is given
by
f=R1R2/(n-1)(R2-R1). Calculated values for
p2
and q2
are substituted in Eq. 49 to obtain the rear lens aberration
coefficient s2.
For cancelled spherical aberration, the sum of aberration coefficients
for the front and rear lens must be zero. This can be achieved only for
a single value of the refractive index n, that is, for a single
wavelength. In a doublet achromat with spherical aberration cancelled
for the e-line, the blue end of spectrum will be overcorrected and the
red end under-corrected (FIG. 70). However, the error is generally
low. Chromatic spherical aberration - or spherochromatism - remains
negligible in most doublet achromats, the exceptions being larger, fast
achromats, for instance 6" f/5 or 8" f/6.
 FIGURE
70: Spherochromatism of the red C- and blue F-line in a 100mm
f/10 achromat shows as bending of the LA plot away from vertical.
The bending is a consequence of different zones focusing at a
different distance from the objective due to spherical aberration. In an achromat with spherical aberration corrected for the green FIGURE
70: Spherochromatism of the red C- and blue F-line in a 100mm
f/10 achromat shows as bending of the LA plot away from vertical.
The bending is a consequence of different zones focusing at a
different distance from the objective due to spherical aberration. In an achromat with spherical aberration corrected for the green
e-line (hence with rays from all zones of the lens objective coming
to a common focus), the blue
wavelengths are overcorrected (marginal rays focusing farther away than
the paraxial), while the red wavelengths are under-corrected. This
spherochromatic error is, however, only a small fraction of defocus
error due to secondary spectrum. In this case, the P-V wavefront
error of spherical aberration is only 0.043λ in the F line, and
0.055λ in the red (right). The total error changes with how close
are F and C lines positioned: when their best foci coincide (top left), defocus+spherochromatism is little over 1.4 waves P-V in the blue,
and 1 wave in the red. The two are balanced, each at little over 1.2
wave P-V, their marginal foci nearly coincide (top right). If the paraxial blue and red foci are
coinciding (not shown), the best red focus - the one for 0.707 zone
- is closer, and best blue focus
farther away from the
e-line (green) best focus, with the greater defocus
error in the blue making color correction slightly imbalanced.
In any case, spherochromatic error is negligible
in comparison.
In apochromatic objectives,
due to their more strongly curved surfaces, spherochromatism is often
significant, commonly involving both, lower- and higher order spherical
aberration. Calculation for the latter are more complex, and usually
dealt with using ray trace programs. The main difference versus primary
spherical is that secondary spherical cannot be fully corrected (without
putting a Schmidt-type aspheric on surface), only
minimized to nearly 1/6 of its magnitude, by offsetting it with the
primary form. Hence it can significantly affect the optimized wavelength
as well.
More details about spherochromatism in refracting objective can be found
in Lens objective page.
◄
4.7. Chromatic aberration
▐
4.7.2. Lateral color error
►
Home
| Comments |
FIGURE 69: Position factor p of a thin lens
changes with the lens type (positive/negative) and the properties of
light cone incident to it, with respect to lens' focal point
F and the resulting image
separation i, as given by
p=1-2f/i.
FIGURE
70: Spherochromatism of the red C- and blue F-line in a 100mm
f/10 achromat shows as bending of the LA plot away from vertical.
The bending is a consequence of different zones focusing at a
different distance from the objective due to spherical aberration. In an achromat with spherical aberration corrected for the green