telescopeѲptics.net   ▪   ▪   ▪  ▪ ▪▪▪▪ ▪ ▪  ▪   ▪    ▪     ▪      ▪       ▪        ▪         CONTENTS
 

◄ 3.5.2. Zernike aberrations   ▐    4. INTRINSIC TELESCOPE ABERRATIONS ►
 

3.5.2. (cont.) Zernike aberration terms

Since both, standard aberration functions and Zernike aberration polynomials, are describing the same wavefront deviations, they can be related and converted from one form to the other.

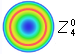
Denoting Zernike aberration terms - the orthonormal Zernike polynomials - simply as Za (full designation , usually written as or, in a single-index notation, as Zj, informally - and incorrectly - referred to as "Zernike coefficients"), and corresponding Zernike expansion coefficients as za (usually written as cnm, here znm), where the term subscript a identifies the corresponding aberration as primary spherical (S), coma (C) or astigmatism (A), Zernike polynomial form for these three point-image quality primary aberrations can be related to the peak aberration coefficients S, C and A from Eq. 5.1 as follows:

- spherical aberration:    ZS =  zS√5(6ρ4-6ρ2+1)  =  |S|(6ρ4-6ρ2+1)/6,   with n=4, m=0, thus ZS=Z and zS=z40
- coma:    ZC = zC√8(3ρ3-2ρ)cosθ  =  |C|(3ρ3-2ρ)cosθ/3,   with n=3, m=1, thus ZC=Z, and zC=z31
- astigmatism:     ZA= zA√24(cos2θ-0.5)ρ2  =  |A|(cos2θ-0.5)ρ2,   with n=2, m=2, thus ZA=Z and zA=z22

with "||" indicating absolute - i.e. w/o numerical sign - value (note that the sign of m superscript and corresponding cosine function are according to the angle convention used on this site)

This implies that Zernike expansion coefficients zS, zC and zA, equal the corresponding RMS wavefront error ω, which is in terms of the peak aberration coefficient given by ωS=|S|/6√5=|S|/√180, ωC=|C|/3√8=|C|/√72 and ωA=|A|/√24 for spherical aberration, coma and astigmatism, respectively. With respect to the Zernike aberration term, ωS=zS=ZS/√5, ωC=zC=ZC/√8 and ωA=zA=ZA/√6 (coma and astigmatism along the ais of aberration, i.e. for θ=0).

Note that RMS wavefront error is by definition numerically positive, unlike peak/P-V wavefront error, or Zernike expansion coefficients, which can be numerically negative.

Similarly, conversion for defocus is ZD= zD√3(2ρ2-1)= Pρ2/2, with n=2, m=0, thus ZD=Z and zD=z20 implying ωD=zD=ZD/2√3.

Note that these relations are for best focus location; also, in order for the nominal error to reflect its actual effect on diffraction intensity distribution, expressing the expansion coefficients as representing the RMS wavefront error requires the latter to be nearly identical to the phase factor φ of standard deviation, i.e. phase error averaged over the pupil (requirement fulfilled for low-level aberrations affecting most or all of wavefront area, roughly below λ/2 P-V in magnitude).

The above relations are valid for clear aperture (Zernike circle polynomials/coefficients). To an aperture with central obstruction applies different polynomial form (Zernike annular polynomials/coefficients). In this case, all three - RMS wavefront error, Zernike expansion coefficient and Zernike aberration term change according to a factor appropriate to each aberration form. Specifically,

ωSo= zSo = ZSo/√5 = ωS(1-o2)2 = zS(1-o2)2= ZS(1-o2)2/√5

ωCo= zCo = ZCo/√8 = ZC(1-o2)(1+4o2+o4)1/2/√8(1+o2)1/2  and

ωAo= zAo= ZAo/√6 = ZA(1+o2+o4)1/2/√6

for primary spherical aberration, coma and astigmatism, respectively, with o being the relative obstruction size in units of the aperture.

Following table gives an overview of the Zernike aberration forms for the most common monochromatic aberrations in telescopes, for clear circular aperture (aberrations in aperture with central obstruction are described with Zernike annular polynomials). The three point-image aberrations, spherical, coma and astigmatism, are balanced, with "balanced" as before, referring to the principal aberration form that combines two or more secondary aberrations in order to reduce error to a minimum (i.e. to the level at its diffraction, or best focus).

For instance, balanced primary spherical includes its principal aberration term ρ4 and balancing defocus term ρ2, coma includes its principal aberration term ρ3 and balancing tilt term ρ, secondary spherical, also in its balanced form (minimized by combining it with 4th order spherical and defocus, thus here referred to as balanced 6th/4th order spherical aberration, in order to distinguish it from balanced pure 6th order aberration, which is minimized by combining it with defocus alone) includes its principal aberration term ρ6 and two balancing terms, for lower-order spherical and defocus (ρ4 and ρ2, respectively). The polynomial forms are as given by Mahajan (Optical Imaging and Aberrations).
 

ZERNIKE CIRCLE POLYNOMIALS FOR COMMON ABERRATIONS (BEST FOCUS LOCATION)

I

II

III

IV

V

VI

ABERRATION

n

m

ORTHOGONAL
POLYNOMIAL
P (ρ,θ)=V(ρ)cos(mθ)=P

ORTHONORMAL
POLYNOMIAL
 P'=NP
N=[2(n+1)/(1+δm0)]0.5

ZERNIKE
ABERRATION TERM
Z (ρ,θ)=P'znm=NPznm=Z

RMS ERROR
(EXPANSION
COEFFICIENT)
ωz=znm
 =Z/N

Tilt (Distortion)

1

1

ρcosθ

2ρcosθ

[2ρcosθ]z11

Ztd/2

Defocus
(Field curvature)

2

0

2ρ2-1

√3(2ρ2-1)

[√3(2ρ2-1)]z20

Zd /√3

Spherical

primary
(best focus)

4

0

6ρ4-6ρ2+1

√5(6ρ4-6ρ2+1)

[√5(6ρ4-6ρ2+1)]z40

Zs1/√5

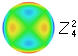
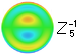
secondary (balanced 6th/4th)

6

0

20ρ6-30ρ4+12ρ2-1

√7(20ρ6-30ρ4+12ρ2-1)

[√7(20ρ6-30ρ4+12ρ2-1)]z60

Zs2 /√7

 Coma

primary

3

1

(3ρ3-2ρ)cosθ

√8(3ρ3-2ρ)cosθ

[√8(3ρ3-2ρ)cosθ]z31

Zc1/√8

secondary

5

1

(10ρ5-12ρ3+3ρ)cosθ

√8(10ρ5-12ρ3+3ρ)cosθ

[√8(10ρ5-12ρ3+3ρ)cosθ]z51

Zc2/√8

Astigmatism

primary

2

2

ρ2cos2θ

√6ρ2cos2θ

[√6ρ2cos2θ]z22

Za1/√6

secondary

4

2

(4ρ4-3ρ2)cos2θ

√10(4ρ4-3ρ2)cos2θ

[√10(4ρ4-3ρ2)cos2θ]z42

Za2/√10

TABLE 5: Zernike circle polynomials for selected balanced (best focus) aberrations.
COLUMN I; "primary" refers to the lower, or 4th order wavefront aberration form, with n+m=4, and "secondary" to the subsequent higher, or 6th order form, with n+m=6 (in terms of ray aberrations, 3rd and 5th order, respectively);
COLUMN II: integers specifying Zernike mode; the subscript n, or radial order, is the highest exponent of ρ in the radial variable (analog to the exponent of normalized pupil height factor in the standard aberration function); superscript m specifies angular frequency of the mode, with positive integers - such as those given in the table - indicating change in deviation with cosine of the angular coordinate θ, and negative integers indicating its change with sine function (numerically, m is analog to the radial power in image space for standard aberration functions);
COLUMN III: General (orthogonal) form of the Zernike circle polynomial, V(ρ)cos(mθ), is a product of its radial variable V(ρ) and angular variable cos(mθ);
COLUMN IV: Orthonormal Zernike polynomial, normalized with a factor N=[2(n+1)/(1+δm0)]1/2 that scales it to unit variance; in effect, the normalizing factor N scales the value of the polynomial to its RMS error level, which makes polynomial values for different aberrations directly comparable, as well as additive/subtractive; it is directly related to the manner in which zero mean splits the wavefront: as FIG. 32 illustrates, with primary spherical aberration, the P-V wavefront error split relative to zero mean is proportional to (1+0.5), with the P-V/RMS ratio given by 1.5√5; for balanced secondary, the split is even, proportional to (1+1), with the P-V/RMS ratio given by 2√7 (FIG. 37C); for tilt, defocus, primary coma and astigmatism (last three, FIG.30-1), the wavefront
P-V split vs. zero mean is proportional to (1+1) and the P-V/RMS factor is given by 4, 2√3, 2√8 and 2√6, respectively  (δm0 in the normalization factor N is Kronecker delta of m and 0, thus δm0=0 for m≠0 and δm0=1 for m=0); 
COLUMN V: Zernike aberration term, or mode, Z (ρ,θ), a product of the orthonormal polynomial P' and Zernike expansion coefficient znm, the latter equaling the RMS wavefront error in units of wavelength (the aberration term P' is what is popularly called "Zernike coefficient" value given by raytrace programs);
COLUMN VI: Relative (in units of wavelength) RMS wavefront error ωz corresponding to the Zernike aberration term; it is called  Zernike expansion coefficient, and obtained directly from the Zernike aberration term Z as ωz=znm=Z/NP, where coordinates for the orthogonal polynomial P=P (ρ,θ) are set to ρ=1 and θ=0 (thus giving 1 for any orthogonal polynomial P), resulting in ωz=znm=Z/N; denoting Z as a general Zernike aberration term , and terms with subscripts t, d, s1, s2, c1, c2, a1 and a2 as specifically referring to tilt, defocus, primary and secondary spherical, coma and astigmatism, respectively, the RMS error is obtained directly from the term value as indicated (obviously, any specific RMS error can be directly assigned the corresponding Zernike aberration term as Z=Nωz; for instance, for the diffraction limited RMS ω=1/√180, the corresponding Zernike term value for balanced lower-order spherical aberration is Zs1=Z=√5ω=√5z40=1/6).

Each separate polynomial in the above table describes single aberration of a perfect conical surface, hence only a single polynomial suffices to describe it; since the aberrations are separated, the wavefront orientation is inconsequential for describing the mode of deformation, and all radially non-symmetrical aberrations are given with a positive m integer (i.e. with cosine function in the angular variable).

As mentioned on page top, Zernike aberrations for specific telescope systems, or a mirror, are commonly given in the form of Zernike aberration term, which is, as illustrated on FIG. 31, a product of Zernike orthonormal (normalized to unit variance) polynomial and Zernike expansion coefficient (in effect the RMS wavefront error in units of the wavelength). While formally there is no limit to the number of these terms - or modes - that can be used to describe wavefront structure, relatively smooth wavefronts typically produced by telescope optics are well described by a limited number of Zernike modes. The terms are routinely referred to as "Zernike coefficients" by the amateurs (not seldom, informally, by non-amateurs as well), which is formally incorrect. Zernike (expansion) coefficient is a part of Zernike term; the coefficient equals the RMS error, for optical systems usually given in units of wavelength.

An expanded set of Zernike polynomials includes any chosen number of higher-order terms, in addition to the lower-order terms; in raytracing reports, they are often given in the form of a simple designation zi, with the subscript i indicating term's ordering number, and referred to as Zernike coefficients. This notation is inappropriate, since given values are for the Zernike term, which is always denoted by a capital letter, as opposed to the Zernike (expansion) coefficient - nominally equaling the RMS wavefront error - which is denoted with a small letter.

The first term is always piston - an aberration term associated with chief ray, which only constitutes an aberration in systems with two or more pupils differing in phase. It is normally followed by terms expressing lower-order aberrations, and then those for higher-order forms. Every aberration term except those with full rotational symmetry (defocus and spherical aberration) has two forms, one with cosine, and the other with sine of θ. The sine form effectively rotates wavefront pattern by 90/m degrees counterclockwise (m being, as before, the determinant of angular meridional frequency of the Zernike wavefront mode) with respect to its cosine form, producing wider variety of shapes needed to model asymmetric wavefronts.

Specific terms in a set of Zernike polynomials can vary, according to its purpose. Order of terms (or term expansion) is based on the polynomial ordering number. This number is used for a simplified, single-index term notation. There are several different definitions of the ordering number, with somewhat different forms of term expansion. For evaluating optical systems, one that is commonly used is based on the set of Zernike coefficients defined by J. Wyant (used in OSLO raytracing software). The full set lists 48 Zernike terms; these are the first 15:
 

1

2

3

4

5

6

#

ZERNIKE
TERM
 (often referred to as
coefficient)

Zernike
ORTHOGONAL
circle
polynomial

RMS
ERROR
(Zernike coefficient's
absolute value)

Aberration

WF Map[2]
w/ANSI sign

Name

Standard  aberration function[1]

Paraxial focus

Best focus
*deviation from zero mean

0

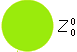
Z0

 1

Z0

piston

-

-

1

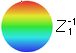
Z1

ρcosθ

Z1 /2

distortion/tilt

ρcosθ

ρcosθ

2

Z2

ρsinθ

Z2 /2

-

-

3

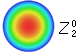
Z3

2ρ2-1

Z3 /√3

defocus/field curvature

ρ2

ρ2
ρ2-0.5*

4

Z4

ρ2cos2θ

Z4 /√6

primary astigmatism

ρ2cos2θ

ρ2(cos2θ-0.5) *

5

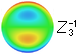
Z5

ρ2sin2θ

Z5 /√6

-

-

6

Z6

(3ρ3-2ρ)cosθ

Z6 /√8

primary coma

ρ3cosθ *

(ρ3-2ρ/3)cosθ *

7

Z7

(3ρ3-2ρ)sinθ

Z7 /√8

-

-

8

Z8

6ρ4-6ρ2+1

Z8 /√5

primary spherical aberration

ρ4

ρ4-ρ2
ρ4-ρ2+1/6 *

9

Z9

ρ3cos3θ

Z9 /√8

elliptical coma
(ARROWS, TREFOIL)

ρ3cos3θ *

ρ3cos3θ *

10

Z10

ρ3sin3θ

Z10 /√8

-

-

11

Z11

(4ρ4-3ρ2)cos2θ

Z11 /√10

secondary
astigmatism

ρ4cos2θ

(ρ4-0.75ρ2)cos2θ *

12

Z12

(4ρ4-3ρ2)sin2θ

Z12 /√10

-

-

13

Z13

 (10ρ5-12ρ3+3ρ)cosθ

Z13 /√12

secondary coma

ρ5cosθ

(ρ5-1.2ρ3+0.3ρ)cosθ *

14

Z14

(10ρ5-12ρ3+3ρ)sinθ

Z14 /√12

-

-

15

Z15

20ρ6-30ρ4+12ρ2-1

Z15 /√7

secondary spherical aberration

ρ6

ρ6-1.5ρ4+0.6ρ2
ρ6-1.5ρ4+0.6ρ2-0.05 *

TABLE 6: WYANT ZERNIKE TERMS EXPANSION (first 15) AND RELATION TO STANDARD ABERRATIONS
 [1] Wavefront error in units of the peak aberration coefficient (S, C, A and P for lower-order spherical aberration, coma, astigmatism and defocus, respectively); ρ is the pupil radius normalized to 1 and θ is the pupil angle. Functions w/o asterisk give P-V wavefront error.  Functions with the asterisk give relative wavefront deviations form zero mean circle; they equal peak (i.e. one half P-V) wavefront error, except for primary spherical aberration, where zero mean splits the P-V error in (2/3):(1/3) proportion, as shown below. For instance, for the peak aberration coefficient S=0.00055mm, the maximum negative deviation given by the peak wavefront aberration relation WP=(ρ4-ρ2+1/6)S, is -1/12 (in units of 550nm wavelength, thus with S=1) for ρ=√0.5, and the maximum positive deviation, for ρ=0 and ρ=1 is 1/6, for λ/4 P-V error (at paraxial focus, WP-V=Sρ4, or 1 wave).
[2] According to the convention, measuring radial angle θ from x+ toward y+ axis (same as on FIG. 30), with a positive superscript indicating cosine, and negative sine function.  This implies that wavefronts oriented with the meridional peak at 3PM clock position are in the cosine mode, and those with the meridional zero at the same point are in the sine angular frequency mode. As mentioned, angular differential in the angle of orientation between the two is given by 90/m, m being the superscript integer (for instance, going from cosine to sine function rotates wavefront by 90° for primary coma, and by 45° degrees for primary and secondary astigmatism). Combining the variety of forms defined by polynomials makes possible modeling all types of asymmetric wavefront deviations.

Note that Zernike term Zi in columns 2 and 4 is often given in inappropriate small-letter notation (which is appropriate to the coefficient), instead of the proper capital-letter notation; two-index notations at left (column 6, next to the wavefront map), relate Wyant's notation to the ANSI standard indexing scheme, with positive top index m indicating cosine, and negative indicating sine function.

Wyant's Zernike terms expansion can be graphically arranged as shown below, also for the first 15 terms. Ordering scheme is based on the radial factor n', angular frequency m and θ function, so that terms with lower n' and higher m are ordered first and, for given n' and m, cosine function is ordered before sine function.

The scheme has inherent symmetry, in that specific general forms of wavefront deformation become more complex going down vertically, as the higher-order terms develop additional "wrinkles". For instance, for n'=4, the first next term for m=0 (radially symmetrical deformations) is tertiary spherical aberration (#24), for m=1 it is tertiary coma (#23 and #22 for the sine and cosine function, respectively), for m=2 it is tertiary astigmatism (#21 and #20), for m=3 secondary trefoil (#19 and #18) and for m=4 quadrafoil (#17 and #16).

One important difference with respect to other expansion schemes is substitution of the conventional radial order n with (2n'-m) in defining the polynomials, and using n'=(n+m)/2 as a term-defining integer in place of n. In the original paper, n' is denoted by n, same as the conventional radial order integer which is, by definition, the highest power over ρ in the polynomial; since the two are numerically different, the original notation here is changed from n to n' in order to avoid confusion. The polynomial ordering number is used for identifying specific Zernike terms in a single-index notation, as shown in the table at right.

Another Zernike ordering scheme used in the telescope optics domain (e.g. ZEMAX standard Zernike coefficients), based on Noll's concept, is shown below for the first 21 terms. Here, the ordering number j is determined by ordering polynomial with lower radial order first, and for given radial order with odd number for sine function and even number for the cosine.

Noll's scheme also has a vertical expansion symmetry similar to Wyant's, but since it directly uses radial order n, it unfolds somewhat differently. So for n=6, the term for m=0 is secondary spherical aberration (j=22), for m=2 it is tertiary astigmatism (j=23 and 24 for the sine and cosine function, respectively), for m=4 it is secondary quadrafoil (j=25 and 26) and for m=6 the hexafoil (j=27 and 28).

Yet another relevant Zernike ordering scheme is ANSI (American National Standards Institute) standard single-index scheme (Zernike pyramid) routinely used in ophthalmology for evaluating eye aberrations.
 

EXAMPLE: Zernike wavefront analysis of a 6" f/8 sphere at 0.25° off-axis. OSLO (which, as mentioned, uses Wyant's expansion scheme for term notation) gives the following non-zero values in the first four decimals: Z1=0.008024 for the tilt, Z3=0.007947 for defocus, Z4=0.041248 for the lower-order (primary) astigmatism, Z6=-0.196736 for lower-order coma, Z8=0.175973 for lower-order spherical, Z13=-0.000245 for the higher-order (secondary) coma, and Z15=0.000181 for the secondary spherical (as mentioned, this coefficient is for the balanced form of secondary spherical aberration, or 6th/4th order higher spherical aberration; pure unbalanced secondary spherical will be quantified mostly through the balanced primary spherical coefficient - Z8 - with a smaller residual in Z15, because its wavefront deformation more closely resembles that of the former).

Multiplying the coefficients with the corresponding unit variance RMS values from TABLE 5 (column 6, with the unit variance RMS being 1/N; they are also given in TABLE 4, column 4, for Zi=1) gives the RMS wavefront error (in units of the wavelength) as Z1 /2 or 0.004012 for the tilt, Z3/√3 or 0.004588 for defocus, Z4/√6 or 0.016839 for primary astigmatism, Z6/√8 or 0.069557 for primary coma, Z8/√5 or 0.078698 for primary spherical, Z13/√8 or 0.000087 for secondary coma, and Z15/√7 or 0.000068 for secondary spherical. The RMS values for lower-order spherical, astigmatism and coma agree with those obtained with standard calculation, given with Eq. 68.2, 70.1 and 71.1, respectively.

The secondary spherical RMS value does not correspond to the actual magnitude of this aberration form in a 6" f/8 sphere. As mentioned, the corresponding Zernike coefficient refers to the fully balanced 6th order spherical aberration, which combines pure 6th order spherical, pure 4th order spherical and defocus in order to minimize the aberration (elsewhere in this site it is referred to as balanced 6th/4th order spherical aberration). The P-V error of pure 6th order spherical aberration for mirror surface at paraxial focus is given by Ws6p=(K+1)2d6/8R5, so its magnitude in a 6" f/8 sphere is 0.000000283mm, or 0.000515 in units of 550nm wavelength. Its RMS wavefront error is smaller by a factor of ~0.3, or ~0.000155. When balanced with defocus, the RMS value of the aberration is minimized by a factor of ~0.4, to ~0.000062 (if now combined with a similar amount of 4th order spherical, the RMS reduces to ~0.00001 wave of fully minimized 6th order spherical). Since the above set of Zernike coefficients does not contain one corresponding to balanced 6th order aberration, it is substituted with a similar RMS value of balanced 6th/4th order spherical aberration, Since the latter is a product of similar amounts of 6th and 4th order aberrations, each about six times greater in their RMS magnitude than that of the fully minimized 6th order spherical, the calculation adds as much to the mirror's 4th order component. This, in effect, produces a combination of wavefront forms that corresponds to the mirror's inherent ratio of 4th and 6th order components, resulting in the identical combined wavefront.

That implies that the above conversion relations for spherical aberration will give accurate result for the lower-order only when the higher order term is comparatively negligible, and vice versa, which is usually the case in amateur telescopes (similar limitations may apply to other aberrations as well). Also, Zernike terms for other aberrations need to be comparatively low; if they are not, it indicates asymmetrical wavefront deformation, with the overall RMS value possibly significantly different from that for the spherical aberration component alone.

In addition, the above conversions are valid for clear aperture. In the presence of central obstruction, the RMS error changes somewhat, depending on the relative size of obstruction o and type of aberration, as noted earlier. Both, Zernike aberration term and expansion coefficient should change in proportion. For instance, with 0.25D c. obstruction (o=0.25), all three, the RMS error, ZS and zS, are reduced by a (1-o2)2=0.88 factor.

Neglecting higher-order terms, the actual wavefront of a 6" f/8 sphere 0.25° off axis (leftmost) can be decomposed to its two most significant Zernike terms: (1) primary spherical aberration term, with the wavefront map (middle) also including negligible defocus term (it has reversed peak compared to the pattern above because it shows undercorrection), and (2) primary coma term, whose wavefront map is slightly altered by low primary astigmatism and tilt components (right).

Note that the Zernike coefficients given by OSLO were for 550nm wavelength. Their values change in inverse proportion to the wavelength, hence these same values would imply larger error with longer wavelengths, and vice versa. Same as with the standard P-V and RMS wavefront errors, determining specific error level from any given set of Zernike coefficients requires knowledge of the wavelength for which they were calculated.

Another example of interpreting Zernike coefficients is given with wavefront analysis of an off-axis segment mirror.

 
 ◄ 3.5.2. Zernike aberrations    ▐    4. INTRINSIC TELESCOPE ABERRATIONS ►
 

Home  |  Comments