telescopeѲptics.net   ▪   ▪   ▪  ▪ ▪▪▪▪ ▪ ▪  ▪   ▪    ▪     ▪      ▪       ▪        ▪         CONTENTS
 

◄ 3.5. Aberration function   ▐    3.5.2. Zernike aberration coefficients ►
 

3.5.2. Zernike aberration polynomials

An alternative way of describing best focus telescope aberrations are Zernike circle polynomials. These polynomials, introduced by the Dutch scientist Fritz Zernike (Nobel prize laureate for the invention of phase-contrast microscope) in 1934, can be applied to describe mathematically 3-D wavefront deviation from what can be constructed as a plane - i.e. unit circle - of its zero mean, defined as a surface for which the sum of deviations on either side - opposite in sign one to another - equals zero. Each polynomial describes specific form of surface deviation; their combined sum can produce a large number of more complex surface shapes, that can be fit to specific forms of wavefront deviations (aberrations). In principle, by including sufficient number of Zernike polynomials (commonly referred to as terms), any wavefront deformation can be described to a desired degree of accuracy.

The usual way of applying Zernike terms is to the specific wavefront shape, which is "decomposed" to a needed number of terms in order to determine: (1) the main forms of contributing deviations, and (2) the overall magnitude of deformation.

For simple aberration forms, such as pure Siedel aberrations, a single polynomial suffices. Describing more complex aberrations, such as, for instance, seeing error, as well as wavefronts formed by actual (i.e. imperfect) surfaces, requires an expanded set of Zernike polynomials.

Zernike polynomials define deviations from zero mean as a function of the radial point height ρ in the unit-radius circle and its angular circle coordinate θ, which is the setting of a telescope exit pupil, in which the wavefront form is evaluated (FIG. 30, 1). In polar and Cartesian coordinates, respectively, the radial component is ρ2=x2+y2, with 0≤ρ,x,y≤1. The common convention for the angular coordinate θ varies with the field; in ophthalmology, it is counterclockwise from x+ toward y+ axis (OSA recommended), thus ρ=x/cosθ=y/sinθ. In general optics, it is often different. Malacara's convention is clockwise from y+ to x+ axis, thus ρ=x/sinθ=y/cosθ, and Mahajan's convention (Optical imaging and aberrations) applied here to the conventional aberration functions is counterclockwise from y+ to x-, hence with the same radial-to-angular relations as Malacara's. The polynomials are orthogonal (i.e. their values change independently, as illustrated on FIG. 30, 1) over the circle of unit radius. Due to this attribute, these aberration forms are termed orthogonal, or Zernike aberrations.
 



FIGURE 30: (1) The unit circle based expansion of Zernike polynomials can be applied directly to wavefront evaluation in the telescope pupil. Orthogonal attribute of the polynomials can be graphically presented as two orthogonal lines for which changes in the value along one do not affect values along the other one.  (2) wavefront deviations as a function of the radial and angular polynomial variable are defined with respect to zero mean circle, which may and may not coincide with the best reference sphere; with Siedel aberrations, zero mean plane splits the wavefront in two halves, the exception being spherical aberration, where the split is in proportion 1:2. (3) Angular variable cos(mθ), or sin(mθ), determines frequency of meridional peaks and valleys, their even or odd number, and orientation of the particular Zernike mode. Shown is OSA-recommended convention of measuring θ, which indicates cosine for wavefronts oriented with the meridional peak toward 3PM, and sine for wavefronts oriented with meridional zero in that direction (the former indicated with a "plus" sign in the superscript, and the latter with a "minus" sign). Radially symmetrical aberrations, like spherical (top) do not have angular variable; primary coma wavefront error (middle) changes meridionally with sin or cosθ (with the former for the pattern shown), and primary astigmatism with sin or cos(2θ) - the latter with this specific pattern. The cosine term is called symmetric function, the term originating from Noll's expansion scheme, were the cosine function alone is used to describe pure conic surface aberrations, like coma and astigmatism, which are radially symmetric in the sense that |cosθ|=|cos(θ+180)|, i.e. the function over two opposite radii on any meridian have identical form, although can be opposite in sign (as illustrated with white meridians over the wavefront maps for coma and astigmatism on FIG. 30, 3). The sine function is called asymmetric, or antisymmetric, not because it itself lacks this symmetry, but because it is combined with the cosine function in order to describe wavefront shapes lacking this symmetry form.  (4) Different forms of aberrations require different power integers over the radial pupil variable ρ and angular pupil variable θ. In general, the former is denoted by n (the highest power), and the latter by m. Numerically, n and m equal the power over radial coordinate and image point height coordinate in the standard aberration function, respectively. In one of the three common Zernike ordering schemes, ANSI standard, the aberration term is denoted by Z, with the sign of m determining the trigonometric function used (- indicates sine and + cosine function, which in turn determine the orientation of wavefront deformation in the coordinate system), while the integer itself determines the frequency of meridional peaks and valleys.

As mentioned, zero mean is defined as a surface for which the sum of wavefront deviations to either side is zero. That is important conceptual difference vs. standard wavefront error, which expresses deviations from a reference sphere (also commonly constructed as a circle). Hence the polynomial, which is a product of its radial variable in ρ and angular variable in θ, has zero value at the intersection of the wavefront and its zero mean. Zero mean differs from the reference sphere for balanced primary spherical aberration and defocus, while coinciding with it for balanced primary astigmatism. coma and balanced 6th/4th order spherical (FIG. A, 2). As a result, the form of polynomial is  different from the classical aberration function for the former three, while identical (except for the normalization factor) for the latter two.

The polynomial normalization factor fulfils the formal requirement that the radial polynomial portion equals 1 for ρ=1. For instance, the deviation from zero mean for primary spherical aberration - whose polynomial only has the radial component - is given by ρ4-ρ2+1/6; thus, its normalization factor is 6, and the corresponding Zernike circle polynomial is 6ρ4-6ρ2+1 (this normalization to unit radius shouldn't be confused with normalization to unit variance, described ahead).

Orthogonality of Zernike polynomials creates the possibility to combine as many different surfaces as needed to approximate the form of wavefront deviation with desired accuracy. It allows expressing separate contributions of various forms of aberrations - including any chosen extent of the higher order forms - and obtaining the combined variance as the sum of individual aberration variances. Also, the polynomials can  be - and routinely are - scaled to unit variance over the circle radius for all aberration forms, so that their combined form can be determined directly by adding up their expansion coefficients, which determine the specific magnitude for each aberration form. Wavefront is described as a sum of Zernike aberration terms (FIG. 31).


FIGURE 31: Structure of the Zernike aberration term describing wavefront profile as the deviation from zero mean, the imaginary surface splitting wavefront deviation in two halves of identical aggregate deviation. Any wavefront form can be described as a sum of specific Zernike wavefront terms (or modes), each represented by a product of its specific Zernike orthonormal polynomial and specific value of its Zernike expansion coefficient. Each Zernike term consists of:
(1) specific Zernike orthogonal circle polynomial, describing that particular form of deviation from zero mean,
(2) normalization factor for scaling different Zernike modes to unit variance which, multiplied with the corresponding orthogonal polynomial defines the
(3) orthonormal Zernike circle polynomial, and
(4) Zernike expansion coefficient, which in its absolute value equals the RMS wavefront error for the particular Zernike mode, and determines the actual value of the Zernike term, as a product of the coefficient, the normalization factor, and a sum of two two extreme (absolute) values of the polynomial for 0≤ρ≤1, i.e. its P-V wavefront error in units of the maximum polynomial value, which is 1 for ρ=1 and θ=0 (unlike the RMS wavefront error, which is always numerically positive, Zernike coefficient can be both, positive and negative, depending on the orientation of deformation)
Zernike orthogonal circle polynomial, as shown above, consists from the radial and angular variable, determining relative (in terms of radial and angular coordinate of unit circle) location of any point of the specific surface it describes with respect to zero mean. As the description of the Zernike aberration term implies, the RMS wavefront error corresponding to a specific Zernike term - the latter being the numerical value put out by ray tracing programs to quantify Zernike wavefront analysis (and often erroneously called "Zernike coefficient") - is obtained by dividing the term by its normalization factor. As it is shown ahead, the normalization factor always has the form of a square root, except for tilt aberration, where it equals 2.

In the nutshell, the normalization factor N is chosen so that a product of the sum of two extreme values of the polynomial (absolute values, determining the relative magnitude of P-V deviation) and normalization factor equals the P-V-to-RMS wavefront error ratio for the aberration. Hence, multiplying this product with the expansion coefficient - which equals the RMS error for given aberration - yields the P-V wavefront error corresponding to the coefficient. For any value of the polynomial for given pupil coordinate ρ, a product with the normalization factor and expansion coefficient yields, as already mentioned, the wavefront deviation from zero mean for that particular pupil coordinate.

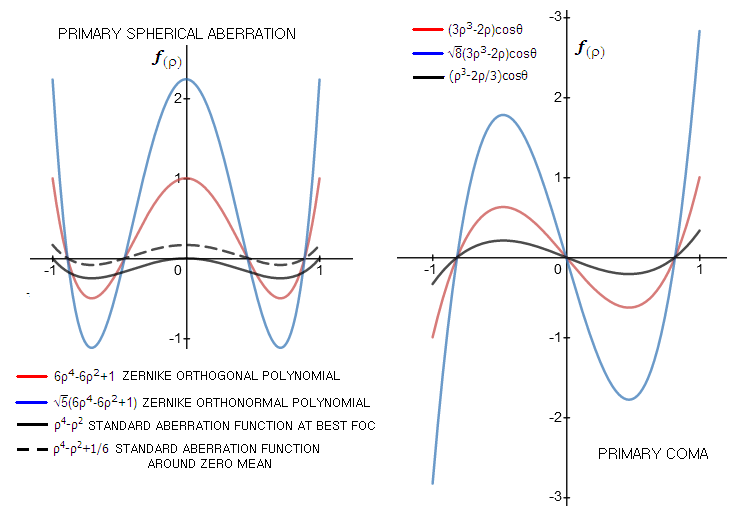
EXAMPLE: Plots for orthogonal and orthonormal Zernike polynomials vs. those of the standard aberration function for primary spherical aberration and coma. All plots for either aberration represent the same type of function - i.e. form of deviation - the only difference being in their nominal maxima or position vs. abscissa (horizontal scale), which represents the pupil, with the pupil radius ρ normalized to unit ranging from -1 to 1. Function f(ρ) - which is the wavefront deviation over pupil (with θ=0 for coma) - shows how the aberration changes over the pupil. In general, plots for Zernike terms have significantly greater amplitude than the corresponding standard functions, due to the coefficients (integer multiplier assigned to the variable) being larger.

For spherical aberration, the standard aberration function relates to the abscissa as the reference sphere; adding numerical constant shifts this function so that the deviation is split equally around the abscissa, which makes the abscissa zero mean for the function. Both, orthogonal and orthonormal Zernike polynomial are constructed around zero mean. The aberration is radially symmetrical, which means that its 3-D shape is formed by rotation of this curve around its center. Orthonormal polynomial is scaled for unit variance by a specific square root multiplier, which further expands its amplitude. The standard function for primary coma is symmetrical with respect to the reference sphere, which in such case coincides with zero mean (as with spherical aberration, the thick darker line is the orthogonal polynomial, thick lighter line the orthonormal, and thin line the standard function). Since coma is not radially symmetrical, its 3-D cross-sections vary with the pupil angle θ (as usual,, it is shown along the axis of aberration, i.e. maximum deviation, for θ=0 and cosθ=1). The unit-variance scaled polynomial (shaded blue, as a side projection of the wavefront deviation from this particular angle) defines coma-shape with the same RMS error as that defined by the unit-variance scaled polynomial (shaded) for primary spherical (coma deviation appears larger due to it showing its maximum, while as the angle in the horizontal plane changes the curve gradually reduce to the straight line (dotted) on both sides of its 3-D shape. For either, spherical aberration and coma, the actual magnitude of deviation is determined by adding the final multiplier to form the Zernike term - the Zernike aberration coefficient. 

As with the standard aberrations, the wavefront error, either P-V (as a direct optical path difference) or RMS, is directly related - although not necessarily identical - to the phase error. The absolute value of Zernike expansion coefficient znm is identical to the RMS wavefront error; since the coefficient does express positive and negative deviations, the sum of coefficients for all Zernike terms used to fit particular wavefront gives its overall RMS wavefront error (i.e. standard deviation), and its square equals the wavefront variance.

The two integers identifying Zernike aberration form are n, the highest order (exponent) in the polynomial's radial variable V (analog to the pupil height factor ρn in the standard aberration functions) and m, the angular frequency of meridional variance (nominally identical to the exponent in the image height factor hm in the standard aberration functions). For radially symmetric aberrations, like spherical, the angular variable cos(mθ) or sin(mθ) is absent, thus m=0 (alternately, since it is independent of the height h in the image space, m=0); and, since the aberration changes with ρ4, n=4. For primary coma, which changes with ρ3 and h, n=3 and m=1; since it varies with the point pupil angle θ, it also includes the angular coordinate factor, in the form cos(mθ).

Consequently, Zernike aberration terms for primary spherical aberration and coma are denoted as Z and Z, and Zernike expansion coefficients as z40 and z31, respectively (note that according to the above convention, m=1 indicates cosine function, i.e. coma peaks are positioned at a horizontal line; for the vertical orientation, m=-1). Likewise, Zernike aberration term and expansion coefficient for primary astigmatism, which changes with the 2nd power in both, pupil and image space (the latter is not formally the basis for indexing, but is numerically correct and convenient), thus with n=2 and m=2 or -2, are Z, or Z, and z22 (which, as any Zernike expansion coefficient, can be numerically positive, or negative, depending on the orientation of deformation). For defocus, which is radially symmetrical like spherical aberration, but changes with the square of pupil height, n=2 and m=0, hence its Zernike term is Z and its expansion coefficient is z20.

As mentioned, every Zernike aberration term (or mode) describes specific orthogonal wavefront deviation from its zero mean, that is, deviations from zero value of the polynomial as a function of change in radial coordinate ρ and angular coordinate θ. How Zernike aberration term - i.e. orthonormal polynomial - specifically describes an aberrated wavefront is illustrated on primary spherical aberration (FIG. 32). For simplicity, the polynomial Z is denoted by ZS and the expansion coefficient z40 as zS; the relative linear wavefront deviation from zero mean as W(ρ), with the corresponding phase deviation Φ(ρ); as usual, the RMS wavefront error is ω, with the corresponding phase RMS error analog φ, and standard phase deviation φ=2πφ (the error variance is, by definition, the standard deviation squared).

Zernike aberration term, either for the phase (ΦS) or wavefront (ZS, identical to W(ρ), the latter being used to relate the nature of it more directly) deviation for lower-order spherical is zero when the sum in brackets is zero. This occurs for ρ2=0.5±1/√12, regardless of the size of aberration, since the sum of deviations between these two zonal heights is identical to the sum of deviations over the rest of the wavefront (which are of opposite sign relative to the plane of zero mean).

FIGURE 32: Zernike circle polynomials can be used to express the two main aspects of wavefront aberrations: linear deviations away from the reference sphere on one side, and closely related to it phase error on the other. The former is described by the wavefront aberration term Z (here written simply as ZS for spherical aberration), and the latter by the phase error term Φ(ρ). The latter expresses orthogonal phase deviation, in radians, from zero mean plane (Φ(ρ)=0), over a circle of unit radius ρ. Unlike the standard wavefront error, which is measured with respect to a reference sphere, Zernike polynomials express the deviation from zero mean. Shown to the left is the primary, 4th order spherical aberration at the best focus, for which zero mean coincides with the plane containing ρ2=0.5-1/√12 and ρ2=0.5+1/√12 zones. The two phase deviation sums - one to the left, the other to the right of the zero mean plane - are equal and of opposite signs (the polynomial itself is zero for these ρ values). The base polynomial - without the standard (phase) deviation value φ - defines relative phase deviation over the pupil. The standard deviation value φ determines its actual nominal value. It is related to the expansion coefficient zs and the RMS wavefront error ω as φ=2πφ=2πzs=2πω (valid for P-V error <0.5λ), with φ being the phase analog to RMS wavefront error (note that unlike the RMS error ω, Zernike coefficient zs can be numerically negative; if the wavefront shown converges to the left - in which case it represents so called "undercorrection" - the deviation adds to the optical path length of reference sphere, with the coefficient value being positive, and vice versa). Since the phase error Φ(ρ) is directly caused by linear wavefront deviations away from the reference sphere, after replacing φ with zs or ω, the polynomial expresses linear wavefront deviation from its zero mean, which coincides with the zero mean of the corresponding phase error. Hence, the two aberration terms relate as Φ(ρ)=2πZs=2πW(ρ), with the term W being used to denote linear wavefront error in this site (note that here it is relative to zero mean, not the reference sphere). It implies that the P-V wavefront error is given by a sum of the absolute values of two opposite maximum deviations from zero mean. In the case of lower-order spherical aberration, as can be seen from the plot, these two maximum deviations are for ρ=0 or ρ=1, and for ρ=√0.5. So, for the RMS wavefront error ω=1/√180, in units of the wavelength, the corresponding P-V wavefront error, given by the sum of either |W(0)| or |W(1)| and |W(√0.5)| is, as expected, WPV=1.5√5ω=0.25, also in units of the wavelength. The corresponding standard phase deviation over the pupil for this RMS error is φ=2π/√180, and the resulting phase error
Φ(ρ)=π/2, both in radians (conversion from the linear to phase error,
and vice versa, is rather direct, with 1 wave of optical path difference corresponding to 2π radians phase difference).

Here, linear wavefront deviation W(ρ), specified by, and equal to the Zernike aberration term, is different form the peak, or P-V value given by the standard aberration form, because zero mean does not coincide with the reference sphere. However, for aberrations where the two coincide - such as primary coma and astigmatism - Zernike aberration term equals the wavefront peak, or P-V error corresponding to the absolute value of Zernike expansion coefficient, i.e. the wavefront RMS error (Zernike coefficient, unlike RMS wavefront error, can be negative, since its sign identifies the spatial orientation of deformation; the sign is determined by the direction of wavefront deviation from reference sphere, along the axis of aberration: if it adds to the OPL, coefficient is positive, and vice versa - on the above illustration, for wavefront converging to the left, the deviation adds to the OPL, and the sign of coefficient is positive).

For instance, Zernike term for primary coma, Z=z31√8(3ρ3-2ρ)cosθ, has the maximum value of √8z31 for ρ=1 and θ=0, cosθ=1 (i.e. along the axis of aberration). For the diffraction limited RMS value of the expansion coefficient, z31=1/√180 in units of wavelength, it gives Z=1/√22.5, equaling the peak wavefront error, also in units of wavelength (if the coefficient is quoted in linear units, for instance microns, the term expresses the peak wavefront error in microns). The P-V error is doubled, since the other, opposite in sign extreme value of the polynomial is identical in its relative magnitude, for θ=180°, cosθ=-1.

Likewise, Zernike term for primary astigmatism Z=z22√6ρ2cos2θ, with the maximum value of √6z22, also equals the peak wavefront error for any given expansion coefficient (i.e. RMS). Even for defocus, where zero mean and reference sphere do not coincide (FIG. 30, 2), Zernike aberration term Z=z20√3(2ρ2-1) will equal the peak wavefront error (for ρ=1), because the zero mean splits the maximum wavefront deviation in two halves.

As another example, Zernike aberration term for 6th order spherical aberration - the form that is optimally balanced with  4th order spherical - is given by the polynomial ZS = √7(20ρ6-30ρ4+12ρ2-1)zS. The zero mean is at the plane containing √0.5 zone (for pupil radius normalized to 1) - as well as two others for which the polynomial is zero - on the wavefront deviation plot. The P-V wavefront error is determined by a sum of the absolute values of maximum deviations from the zero mean, which occur for ρ=0 and ρ=1. With ZS=W(ρ), and zS=ω (the RMS wavefront error), this gives the P-V wavefront error as W=2√7ω. Since the P-V wavefront error for lower-order spherical aberration, as already mentioned above, is a sum of the deviations for ρ=1 or ρ=0, and ρ=√0.5, it is given by W=1.5√5ω, and its P-V error for given (identical) RMS wavefront error relates to that of the balanced 6th order aberration as 1.5√5/2√7.

Another interesting property of Zernike aberration terms implicated by FIG. 32 is that the P-V/RMS ratio can be expressed as (1+d)N, where d is the maximum relative wavefront deviation from zero mean (as an absolute value) to the side opposite to the reference sphere - which is always in the plane containing the vertex - in units of the deviation from zero mean toward reference sphere, and N is the term's normalization (square root) factor. For most aberrations (all primary aberrations except spherical, as well as all secondary aberrations, including trefoil and spherical), |d|=1 and the P-V/RMS ratio is given by 2N. So for coma, with the normalization factor equaling √8, the P-V/RMS ratio is 2√8, and for astigmatism, with normalization factor √6, the P-V/RMS ratio is 2√6. For primary spherical aberration, as shown on FIG. 32, |d|=0.5 and the P-V/RMS=1.5N=1.5√5.

As already mentioned, most common conic aberrations can be described with a single Zernike aberration term, with either cosine or sine angular function (the choice only affect wavefront orientation). However, in order to describe wavefronts generated by irregular surfaces - with this qualification applying to some degree to all actual optical surfaces - or random aberrations (for instance, wavefront error caused by atmospheric turbulence), multiple Zernike terms, with both sine and cosine orientations, need to be included. Following page presents in more detail the properties of Zernike aberrations for common lower-order aberrations, as well as expanded list of Zernike terms - often inappropriately referred to as "Zernike coefficients" - that includes higher-order aberrations as well.

 
 ◄ 3.5. Aberration function   ▐    3.5.2. Zernike aberration coefficients ►
 

Home  |  Comments