|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
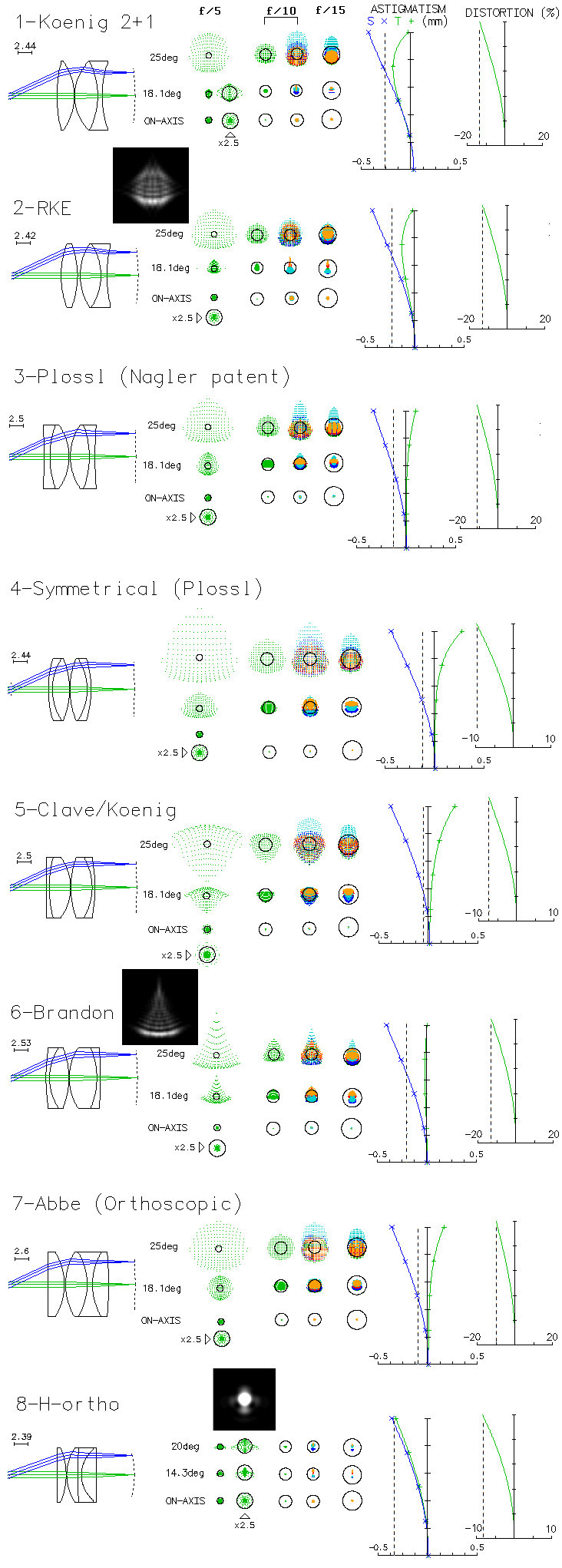
12.4. telescope eyepieceS:
COMPARATIVE RAYTRACING
Individual eyepieces:
Singlet eyepieces
25-40°
40-52°
55-65°
aspheric
over 65°
In order
for any two eyepieces to be comparable with respect to their ray
trace output, they have to be of the same focal length, and used at
the same focal ratio. In general, the larger
focal length at a given focal ratio, the larger geometric blur;
however, since magnification drops in the same proportion, its
angular size, as well as the corresponding diffraction image remains
nearly unchanged (this is valid for relatively large aberrations,
when the ray spot is multiple times larger than Airy disc).
Likewise, the larger relative aperture, exponentially larger the
aberration: primary spherical aberration
with the 4th, primary coma with the 3rd, and
primary astigmatism with the 2nd
power of the change (that is because the relative aperture
effectively determines width of the cone at the field lens, i.e.
eyepiece "aperture").
Eyepieces shown below are all 10mm f.l. at
f/5; they are also
comparable in size, being approximately given in 1:1 scale (FIG.
216). It expands on
FIG. 213 with respect to the number and types of eyepieces
shown, also making the eyepieces comparable in size. Due to that
latter requirement, the simplest eyepiece types are shown smaller,
and some others bigger than the optimum scale. Likewise, the Airy
disc and 5 arc-minute circle are quite small, so that the large
aberrated spots of poorly corrected eyepieces, which are much larger
than those in highly corrected eyepieces, can fit in.
Selection is far from all-inclusive, but attempts to follow the
evolutionary path of telescope eyepiece, from its simplest,
narrow-field forms, to the complex, highly corrected ultrawide-field
examples of our day. Of course, it is also a subject of data
availability. While ray trace output for any given design can vary
in the level of specific aberrations - common trade offs are less
astigmatism for more field curvature and/or coma, or the other way
around - most of the examples shown are within their typical, or
usual mode or according to a specific prescription (e.g. patented
eyepieces).
Ray spot
plots are given for the axial, midfield and near-edge point (except
for the Huygenian and Ramsden, which are shown for their historical
role, being not functional at f/5), in the optimized wavelength
(e-line), as well as the combined
e/F/C spot. Given are the axial Strehl in
the e-line, distortion % for field edge, as well as the approximate
maximum eye accommodation required with respect to the central field
point (for 10mm f.l. every
diopter (D) of accommodation approximates 0.1mm defocus relative to
the vertical plane containing central point; xD of accommodation
approximates one required to refocus from infinity to a 60/x times
17mm distant object). Eye relief, measured from the eye lens, is
given for the midfield and near-edge point (omitted where
negligible); it indicates most of the so called exit pupil spherical
aberration, since the effect becomes generally negligible for field
angles below 20 degrees.
Magnitude of aberration is given relative to the e-line Airy disc. Since
Airy disc has known linear and angular size, it determines linear
and angular size of the ray spot plot. For instance, linear Airy disc
radius, given by 1.22λF, is for given wavelength λ
twice larger at f/10 (i.e. F=10) than f/5. Its angular size depends
on the image scale; twice larger aperture at given F-ratio has doubled
the focal length, hence twice larger image scale, and twice smaller angular
Airy disc, given as 1.22λ/D in radians (times 57.3, 60 and 60
for degrees, arc minutes and arc seconds, respectively), for D
the telescope aperture diameter in the same units as λ.
Apparent spot size is determined by the apparent Airy disc
size, which is given by its angular size in the eyepiece (1.22λF/fe
in radians, times 57.3x60 in arc minutes, for eyepiece f.l. fe).
For the e-line (0.546μ), Airy disc diameter in arc minutes is simply 4.6F/fe.
Light transmission does not show in raytracing, but for older types it averages
about 1% reflection loss per surface for white, green and red light,
about 1.5% in the blue and 2% in violet, due
to reflection, plus about 4% absorption per inch of in-glass travel,
averaged over the spectrum, but also biased toward higher absorption in the shorter wavelengths. Newer
types have about half as much of a loss due to reflection. This applies
to glass-to-air (and the opposite) surfaces. This means that a simplest,
2-surface monocentric would have 1-2% reflection loss in the white light,
while a 8-10 surface "ultrawide" would have it 4-5 times higher, plus
up to several times higher absorption loss.
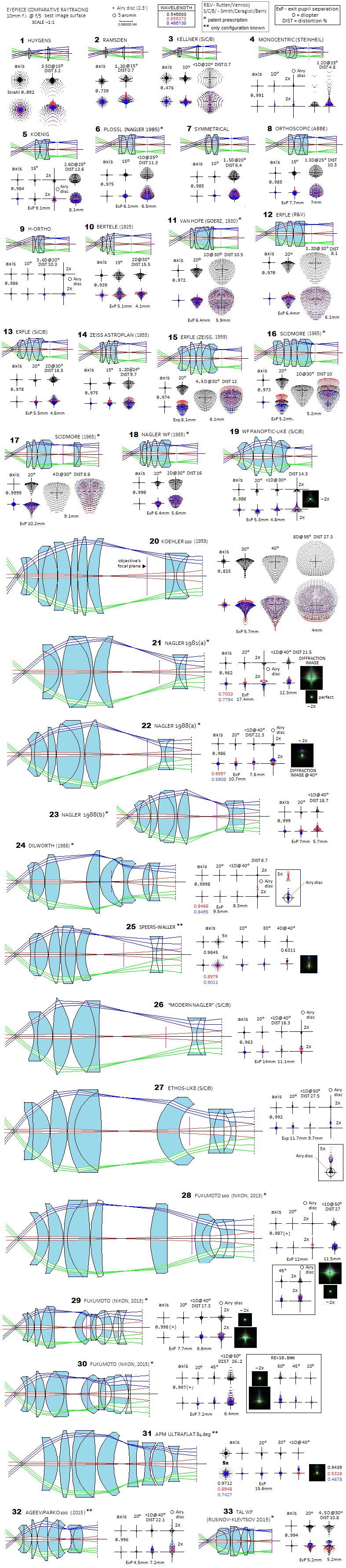
FIGURE 216: 1 -
The Huygenian is pretty much useless at
f/5 due to spherical
aberration (0.24sqrt[-logS] gives 0.24 waves RMS, corresponding to
0.8 wave P-V, which means it requires
f/7 do drop below quarter
wave p-v), but the spots reveal good color correction, and low off
axis aberrations at 15 degrees; field is limited mainly by its
strong Petzval curvature. Lens
separation can be reduced for longer eye relief w/o significantly
altering performance level
2 - Ramsden has significantly better monochromatic
axial correction and mild field curvature, but more of off axis
aberrations. Reducing lens separation vs. classical prescription
increases eye relief, while reducing off axis aberrations, except
lateral color.
3 - Kellner has insufficient axial correction at f/5,
with field limited by astigmatism.
4 - Monocentric - shown is the modern form of this
eyepiece, but performance level is similar to the original -
maintains excellent correction even at f/5, but field is limited by
secondary astigmatism, exploding as field approaches 15 degrees;
since it has a significant higher order aberration component, as
well as primary coma, its aberration load diminishes more quickly
with slower focal ratios than in eyepiece types limited mainly by
primary astigmatism.
5 - Koenig has good overall correction, with the field
limited by astigmatism
6 - Plossl - shown is Nagler's 1985 patent - is
comparable to Koenig (somewhat more of astigmatism is mainly the
consequence of the flatter field)
7 - Symmetrical is similar to Plossl, which may tend
to have marginally better correction, just as the Koenig may have
with respect to Plossl
8 - Classical orthoscopic eyepiece output is very
similar to Plossl's. With comparably thick lenses, it has somewhat
longer eye relief.
9 - The "highly orthoscopic", or H-Ortho has somewhat
different triplet configuration, resulting in a highly corrected
field, similar to that of the monocentric eyepiece, only
significantly wider. In part, this exceptionally good field astigmatism
correction is a trade off for the significantly curved best image
surface. However, while the standard orthoscopic would also have
astigmatism reduced with more strongly curved best field, it doesn't
seem it could achieve the same level of correction.
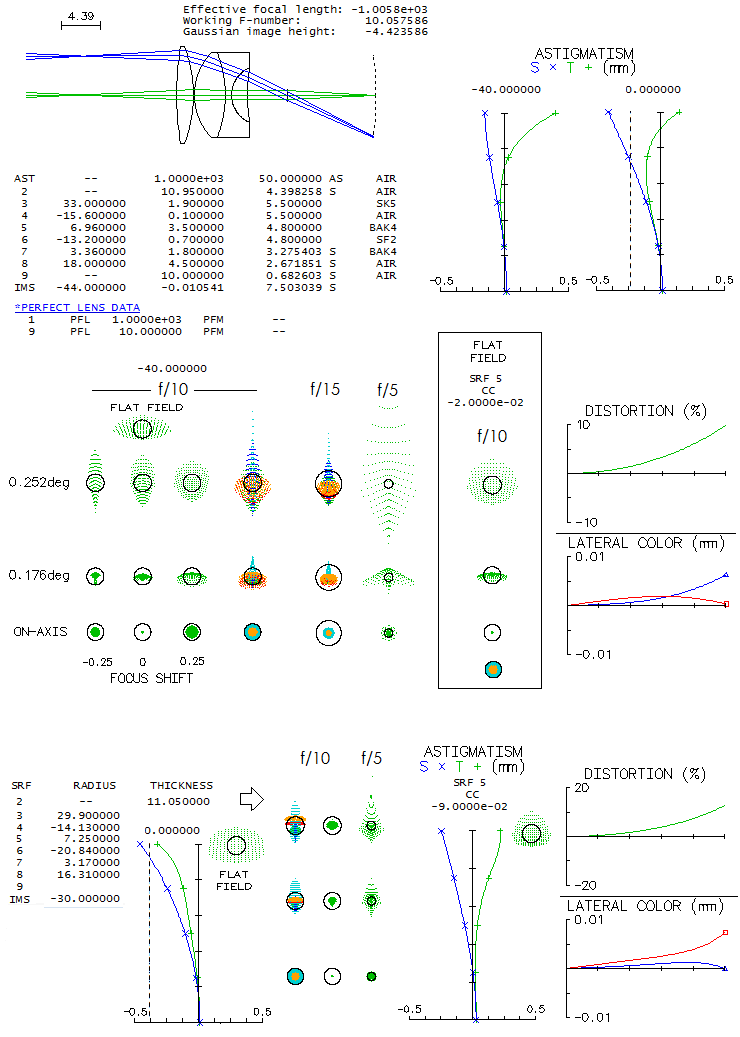
10 - Simple 4-element Bertele
eyepiece from 1925. is an interesting design, in that with some
change in the radii values it can produce astigmatism which at a
certain point reverses from expanding to contracting. So the ray
spot plot is smaller at 30 than 20 degrees off axis and, with larger
lenses, would come to near-zero point closer to 35 degrees off (in
this particular case). If modified this way, its astigmatism 30
degrees off axis is 3-4 times smaller than with the original design.
Its drawback is relatively short eye relief (astigmatism in the more
complex Bertele designs, with 80 and 90 degree AFOV, falls between
the R/V and Zeiss Erfle for comparable field angles but, similarly
to the original Erfle, suffer from significant lateral color
error).
11 - Van Hofe is a well corrected old-type widefield
with a nearly flat field and relatively low distortion.
12 - Rutten and Venrooij's, or R/V Erfle has similar
configuration to the original patent from 1921. but with reduced
astigmatism (20-25%), field curvature and (originally unacceptable)
lateral color.
13 - S/C/B Erfle (Smith/Ceragioli/Berry) is a modern
take on this configuration, with very much reduced astigmatism, but
somewhat reduced eye relief and relatively large distortion.
14,15 - Despite being intended for sub-50° field, Zeiss
Astroplan - another Erfle variation - is, within its field
limits imposed by the lens size, better corrected for astigmatism
than the more complex Zeiss Erfle from 1959.
16,17 - Scidmore 1965 6-element design is better than
the original Erfle, but not from Van Hofe, or Zeiss Erfle. Another
Scidmore design, superficially resembling one with a Smyth lens
(it is a near zero-power lens) may have been an attempt to reduce
lateral color error with still limited choice of glasses.
18, 19 - Nagler's 1985 Widefield further, and
significantly reduces astigmatism in 2+1+1+2 configuration, with
impeccable color correction (Meade's 4000 Series Super Wide was
somewhat rearranged design of this type, with one of the two
singlets used as eye lens, i.e. in 2+1+2+1 configuration;
performance level remains comparable). The next, probably
near-ultimate improvement for this configuration came with the
Nagler Panoptic, whose level of correction should be well
represented with the S/C/B "New WF". Configuration
is similar to the Zeiss Erfle, only with the eye lense front surface even
more curved, and compensated for by more strongly curved outside
radii of the two singlets. That, with somewhat different, simplified
glasses made for a big improvement in the correction level.
The coma-like edge field
aberration is actually predominantly trefoil, as shows on the
diffraction image. It is the first widefield eyepiece that came
meaningfully close to having preserved Airy pattern near the field
edge (see #21).
20 - Koehler 110° eyepiece from 1959 is often seen as
one of a kind with respect to the field size at the time, but there
were similar attempts before (for instance, Slyusarev 100° eyepiece
from 1947). Its significance is in being the first example of the
new, ultra-widefield breed of eyepieces using the Smyth lens. Due to
such configuration, Koehler was able to reduce astigmatism somewhat
within the standard 65-70° widefield, but more so - roughly, nearly
twice (compared to the Slyusarev) - at the 100+ degree mark. To
understand this eyepiece, one needs to know that it was designed as
an integral part of 15x75 binoculars, with
f/5.2 objective lenses. At these field
sizes, these lenses generate significant amount of astigmatism, of
opposite sign to that of the eyepiece, which significantly reduces
astigmatism in the final image. Possibly for the same reason, its
axial correction at f/5
(atypical overcorrection) leaves something to be desired, as it does
its axial chromatic correction, it has short eye relief, and a
massive astigmatism/field curvature when on its own.
21 - Ray spot plots speak clearly why the 1981 Nagler's
"ultrawide" (type 1) marks the beginning of new era, in which highly
corrected eyepieces with 80+ degree AFOV become the standard against
which all others are measured. It has unprecedented field
correction, with the astigmatism reduced to a small fraction of that
in other ultrawide-field eyepieces.
22,23 - The 1988 Nagler (type 2) reaches the level of
astigmatism correction beyond which further improvement becomes of
little practical importance. As the diffraction image for the
Nagler's 1988(a) patent prescription shows 40° off axis, astigmatism
is so low that the Airy pattern is easily recognizable, with the
most obvious aberration being lateral color error (F and C lines are
given increased weight, 0.35 and 0.25 respectively, to show more
clearly the color shift). Correction-wise, further improvement is
limited toward making the residual lateral color negligible; also,
its axial chromatism is larger than in most other eyepiece types,
which is common to all patented Nagler's ultrawides (for F and C
lines, it is in the 0.6-0.8 Strehl range, which compares to, say,
0.85-0.95 Strehl for the top corrected designs, like Dilworth's).
Other possible improvements, such is reduction in size, are not
related to aberrations.
24 - Patent application for Dilworth 90° eyepiece
comes before the Nagler type 2, has wider field and even better
astigmatism correction, but for some reason had never made it onto
the marketplace.
25 - Shown configuration appeared on the Telescope-Express
site as an illustration of the Speers-Waller eyepiece,
thus this represents merely an attempt to see if such configuration
can work. It can. It has obvious similarity to the Nagler 1988(a),
only with the singlet and meniscus switching places, with the latter
turned around to keep the same orientation vs. diverging ray
pencils. In fact, just making the initial design starting with the
Nagler and changing its configuration, roughly trying to preserve
each element's power, resulted in eyepiece design close to the
optimization level. Overall correction achievable is very good, with
the only aberration of some significance being field curvature, at
little over 4 diopters of accommodation - i.e. infinity to about
35cm - required between field center an edge. It nearly certainly
can be reduced w/o significant compromises; appears it could be
easier with somewhat wider Smyth lens separation. Similar
configuration was used for Meade's 4000 Series Ultra Wide,
difference being that both doublets had a positive meniscus shape,
convex side facing the Smyth lens.
26 - Nagler-type eyepieces can come with different number of elements and
configurations; one example given as "modern Nagler" by
Smith/Ceragioli/Berry has correction comparable to the type 2
Nagler, in a somewhat longer train.
27 - Further expansion in the field size led to breaking into
the 100°-120° AFOV range. One example is Ethos-like 100°
eyepiece given by Smith/Ceragioli/Berry, in configuration nearly
identical to the Nagler Ethos. The only residual aberration worth
mentioning is lateral color, comparable in magnitude to that in the
Dilworth's eyepiece. The configuration can be made more compact by
reducing the two widest interspaces, with the lateral color also
significantly reduced. This type of configuration, more or less
modified, is likely used in some other brands (online source¹
supplies evidence that 13mm Ethos and 14mm 100° ES are essentially
identical configuration).
28 - Fukumoto 100° eyepiece (the 1st of 5 examples in
the patent application) is a basis of the Nikon NAV-HW
ultrawide (7/10 arrangement). There is obvious similarity in the
general configuration with the Ethos, but it is also a design with
its own characteristics, such as more complex Smyth lens, and near
non-existent spherical aberration of exit pupil.
29, 30 - Another Fukumoto-Nikon design from the same
time frame is 82° AFOV design with a very complex Smyth lens and
relatively simple positive counterpart. Five of the six examples in
the patent application do not feature the front two singlets; most
have similar edge performance as the one shown here, but somewhat
more astigmatism in the inner field. Reduction in the overall size
is very obvious. Subsequent 2015 Fukumoto-Nikon patent expands the
field of this eyepiece type to 100°. Patented version shown (the
preferred one, out of five) shows very good correction up to 45°, or
so, and the astigmatism flare up toward field edge doesn't show on
the astigmatism graph in the patent application. Since a small
change in one of the radii (R8, box to the right) nearly brings it
to where it should be, there is probably a typo in the patent
prescription.
31 - Design based on the published configuration for APM
"Ultraflat" 84° eyepiece (originally 12.5mm f.l.) with no other data.
It also turned out to be a viable configuration, with a very good correction
over the entire, flat field, and long eye relief.
32 - Ageev-Parko 100° eyepiece (Shvabe, Moscow) is one
of the latest newcomers to this arena. Its patent application only describes
configuration and glasses in general terms, so the design shown above only
illustrates configuration and performance, using Schott glasses (original
glasses are LZOS). The astigmatism plot supplied with the patent application
implies the highest level of correction (noting that astigmatism plot says
nothing about coma or other aberrations possible in this kind of eyepiece, such
is trefoil). Its major advantage is small size, nearly half the length of the
"small" 100° Fukumoto (noting that longer eye relief claimed in the patent would
require larger lenses); eye relief in the patent description is nearly twice
longer.
33 - TAL widefield is a recent modification of the
Rusinov design from the 1970's by Klevtsov. Its field is not as wide, and its
correction level is not as high as in the modern Smyth-type designs, but it is
significantly better than in the conventional widefields. The coma residual
could have been left in on purpose, to compensate for the positive coma
in some TAL telescopes.
¹ http://www.svenwienstein.de/HTML/es_14mm_ethos_13mm_English.html
SPECS.
Individual eyepieces
Due to the large number of eyepiece designes shown, image above could not go into more
detailed account of each one. That will be attempted below, with the
eyepieces organized in four different groups: (1) narrow-field, 25°-40°,
(2) standard field, 40°-50°, (3) standard
widefields, 55°-65°, and (4) Smyth-lens widefields (the field
criteria is based on the usual practice; the possible field size is somewhat
flexible category). In general, the same order
will be followed, with some interesting designs added to those already
presented. Also, some less interesting designes will be omitted.
As before, all units are of 10mm focal length, but in addition
to f/5, ray spot plots will be shown for f/10 and f/15 systems. Spectrum is
also widened, to include the violet g and red r lines.
Since the chromatic errors at fast focal ratios are dwarfed by spherical
aberration and astigmatism, the f/5 ray spot column shows
only green e-line.
Before continuing with complex eyepieces - consisting of two or more lenses - will briefly
address single lens eyepieces. They have historical significance, being the eyepiece of
choice for astronomical observation in most of the 17. century, and even today are in (very)
limited use. Singlet eyepieces were planoconvex, biconvex or spherical (ball eyepiece,
originating in early microscopy). They are analized using direct raytrace, with OSLO
"perfect lens" as objective and the eye, for f/5, f/10 and f/15 focal ratios. Units' focal
length is, as before, 10mm, and field radius is 7°, which is close to the limit imposed by
field curvature. Note that this is for geometry corresponding to the eye lens, i.e. with the
perfect lens (surface #5) f.l. of 17mm. If the focal length was 10mm, image scale would shrink
proportionally, but it wouldn't change with respect to aberrations, because the smaller
longitudinal/transverse error would be offset with smaller Airy disc. However, the best field
curvature, dropping to -1.5mm, would limit usable true field angle to 0.87°, corresponding
to 8.5° eyepiece field radius; this approximatelly corresponds to the output by 10mm unit in
reverse raytracing, but it is not reflecting the actual, eye geometry. The reason angular field
shrinks in size with a longer perfect lens f.l. is that the Petzval curvature doesn't change, but
astigmatism increases in proportion to the focal length; since the two are of the same sign,
i.e. astigmatism makes curvature stronger, more astigmatism makes field more strongly curved
(since at 10mm f.l. the curvature is -1.5mm, if it would change in proportion to the f.l. it
would have been -2.55mm at f=17mm, but it is only -1.95mm).
Yet, as already mentioned, the final judge is not the nominal curvature, but the required eye
accommodation. Since image scale at 17mm f.l. corresponds to that of 17mm eyepiece, the -1.5mm
defocus at the edge of 7° field corresponds to -5.2 diopters of accommodation (from f2/1000),
while -0.55mm defocus at 10mm f.l. (and 8.5° field angle) corresponds to -5.5 diopters.
With the field curvature being caused by the light not exiting eyepiece collimated, but mildly
converging, it requires the eye to relax beyond its infinity mode - unnatural accommodation -
in order to bring light to focus onto retina. In either case the limit to field size is not
impossed by accommodation requrement, but by field curvature, closing 90° angle with
respect to the central point (going beyond this field angle results in the converging cones
focusing yet shorter, but with the best astigmatic focus suspended in front of the preceding
field angle point, becoming more separated, hence undefined).
Starting with planoconvex lens, raytrace for lens with flat side toward eye
shows that its axial correction is perfect at f/15, with longitudinal chromatism and
spherical aberration becoming increasingly intrusive - especially the latter - as relative
aperture becomes significantly larger than f/10. Off axis, dominant aberration is astigmatism,
followed by coma. Lateral color error is not negligible even at f/15, even with field size severely
limited by field curvature. Turning the lens around, convex side toward eye, results in minor
changes off axis: somewhat more astigmatism, and less coma (bottom). However, spherical aberration is
significantly lower.
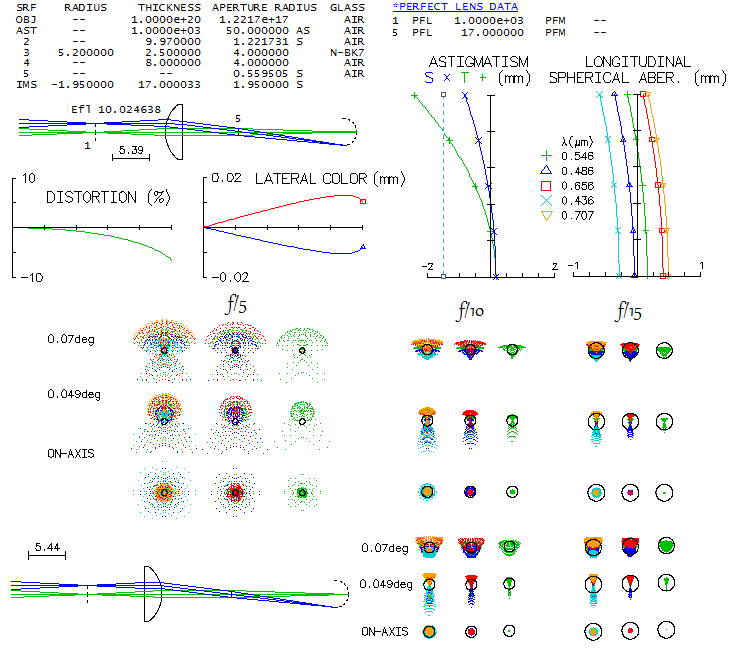
Biconvex lens has noticeably less of astigmatism and field curvature, although the latter is
still allowing only for a rather small field (top). It has also somewhat better correction of spherical
aberration and longitudinal chromatism, with lateral color error of similar magnitude. Ball
eyepiece - which may and may not be a complete sphere - offers still better overall correction
(bottom).
As mentioned, these examples are directly comparable to the other 10mm designs,
most of them reverse raytraced,
except with respect to field curvature, which in direct raytracing varies with the focal length of
the image-forming element. If the perfect lens in place of eye would have 10mm f.l. instead
of 17mm, the field curvature/astigmatism would be very similar to those with the same eyepiece in the
reverse raytracing (with minor differences in the shape of astigmatic field). But the 17mm f.l. illustrates
how the (perfect) eye lens modifies ray geometry
(for this pupil size and field angle, eye aberrations can be considered negligible, or nearly so).
Follow multi-lens eyepiece designs.
25°-40° FIELD EYEPIECES
The first group includes one and two-group lens designs with field diameter
up to 40° (in their original designs). The Huygenian consists of two plano-convex lenses facing objective
with their convex side. It achieves best overall correction with the focal length of the
field lens about twice that of the eye lens, and the lens separation
nearly 40% of their focal length sum. At the canonical equal lens separated
by half their focal lengths for corrected lateral color, aberrations
are too strong, dominated by coma, and including crippling field curvature
due to the strong negative astigmatism being of the same sign as the
Petzval curvature (on top of that, objectve's image falls into the field
lens, and exit pupil forms between the lenses). With the increase
of the field lens f.l. relative to the eye lens, both coma and astigmatism
diminish, coming to their minimum at ~2:1 ratio. Coma can be cancelled, and
weak positive astigmatism begins to countereffect the strong Petzval. Further
ratio increase leads into coma turning negative and larger, as well as positive
astigmatism, softening image curvature at the price of larger wavefront error.
Lens thickness, particularly of the eye lens, is also important aberration factor; also, thinner
lenses, in general, as well as a reduction in lens separation, allow for a
larger eye relief. All these factors matter, and have to be optimized
for the best possible correction. For instance, design posted in "comparative
raytracing" has some significant residual negative coma and lateral color. The coma
can be reduced to non-significant by reducing the eye lens thicknes from 1.25mm
to 0.7mm; eye relief gets shorter by ~0.1mm, and best field curvature goes
from -10mm to -11mm. Increasing lens separation from 10mm to 11mm takes
care of the lateral color, at a price of eye relief reduced to ~2.2mm. Field
curvature, due to the stronger positive astigmatism, goes to -12mm. Reducing
front lens thickness from 1.5mm to 1mm extends the exit pupil to 2.9mm at
15° field angle (at 25° it is only 2.4mm). Such optimization
leads to a Huygenian with clean ray spot plots, as shown here, even
with the spectrum extended on both sides.
The Huygenian is usually limited to ~30° field diameter, not
because of point-image aberrations, but by its strong field curvature.
Nominal field curvature can be misleading: here, radius of a sphere
containing best astigmatic focus for the 15° field radius (on top of the
shortest vertical dashed line) is significantly shorter than the one
containing best focus at 25°, despite the latter being more than
twice more defocused with respect to the central spot. The reason is that
what matters is the sagitta of field curvature - i.e. point coordinate
determined by its height and the radius - not the radius itself. Thus,
it is better to express field curvature in diopters of accommodation.
Good approximation for diopter of accommodation is given by D~f2/1000,
with f being the eyepiece focal length. For a 10mm f.l. every
0.1mm of defocus requires one diopter of accommodation (in terms of
object distance, one diopter represents accommodation from infinity to
1m, and three diopters accommodation from infinity to 0.33m). As the
astigmatism graph shows, this 10mm Huygenian requires over -8 diopters
accommodation at 25° field, nerly -6 diopters at 20°, and -3.5
diopters at 15°. Even -3.5 diopters, or accommodation from infinity
to -29cm can be challenging for some people. The minus sign means that
eye has to deal with diverging pencil of light exiting the eyepiece - since
the field point is closer to the eyepiece than the center point,
forming parallel pencil of light - which is natural to the eye, and much
easier than positive accommodation, when eye needs to relax beyond its
infinity mode. Axial spot at f/10 shows best focus primary spherical nearly
filling up the Airy disc, corresponding to 1/13 wave P-V wavefront error.
Since it changes with the 4th power of focal ratio, at f/5 it would be
16 times greater - or over 1 wave P-V - making the eyepiece useless. Huygenian also has a significant
negative ("barrel") distortion at 25° field radius, but since it changes
with the 3rd power of field angle, it is negligible at its usual field size.
Note that the reverse raytracing image is not the image seen by the eye. Raytracing
follows a perfect parallel pencil entering eye lens, converges toward the
field lens, and exits it converging further toward objective's image (with
most eyepieces; with the Huygenian, objective's image is behind the front lens,
so the rays are diverging after the front lens, and raytrace forms
imaginary focus by extending them backwards, toward eye lens). Eyepiece image is,
in fact, image of the objective which would produce perfectly collimated
exiting pencils and, as such, accurately reflects the eyepiece aberrations.
Image seen by the eye is formed on the retina from near-collimated
pencils entering the eye, with each point projected toward infinity in
the direction of the entering pencil.
The Ramsden, similar to the Huygenian in that consists of
two planoconvex lenses, but facing each other with their convex side,
is plagued with similar problems:
at the lens separation equaling lens focal length (assuming two
identical lenses, as proposed by the original design) needed for corrected lateral color, objective's
image is inside the field lens, exit pupil is on the inner side of
the eye lens for all but very central field points, for which is at the lens,
and field curvature severely limits usable field (with 10mm f.l. unit,
needed accommodation at 10° is over 11 diopters). Reducing lens
separation achieves some positive, even still short, eye relief and
lessens field curvature, but at a price of introducing lateral color.
With a pair of two identical lenses at about 2/3 of the focal length
separation, eye relief at 10° off axis is 2.3mm (only 1.3mm at 15°
yes, these simple eyepieces have that much of the spherical aberration
of exit pupil),
and lateral color is acceptable - with acceptable taken as C and F
lines still within
the Airy disc - up to about 10° field radius. Better
performance is achieved with the field lens of somewhat longer f.l.
than eye lens, as in the design shown (-5.66/8.08mm radii, 0.66/0.96mm
lens thickness, 9.6mm lens separation - 72.5% of one half of the focal
lengths sum). Lateral
color is acceptable up to nearly 15° field radius. Required accommodation
at 15° off axis is -2.5 diopters (as refocusing from infinity
to 0.4m) and eye relief for the same field height is 2.4mm. At f/10,
and more so at f/15, astigmatism
is very low, and distortion is negligible within this field. Best focus
ray spot plot for primary spherical aberration at f/5 is about 4 times
the Airy disc diameter, indicating
0.3 waves P-V wavefront error.
Note that this design differs from the one in "comparative raytracing",
despite both having a longer f.l. field lens and identical f.l. sum. Even with
the other design having smaller lens separation, its eye relief at 15°
is only 0.2mm, due to the weaker eye lens and relatively stronger field
lens. In other words, the stronger eye lens in this design spreads the
converging cones wider, and they are bent down less with the weaker
field lens, so that the aperture stop - i.e. exit pupil - has to move
farther out in order for the final cone direction on the other end of
the eyepiece to become slightly converging toward optical axis.
The Kellner, also known as achromatized Ramsden,
in its basic form keeps the same configuration, but the eye lens is
now a cemented achromat. Although the additional, cemented surface,
allows for better correction of lateral color, it wasn't utilized in
its early versions. This is illustrated by the design given by Rutten
and Venrooij, who did modify those old designs only to the point where
they still retain the basic similarity (very similar in that respect is design
given in the "Handbook of Optical Sytems" by Herbert Gross, as well as some
other quality sources). In adition to the significant
lateral color and short eye relief, the early Kellners had much more of the positive astigmatism,
enough to overpower the strong negative Petzval so much that the resulting
best image field had a positive curvature - i.e. curving toward the
objective - almost as strong as the negative curvature of the Ramsden (as
mentioned before, this form of curvature, requiring accommodation to the
converging beams, is much harder on the eye). Smith/Ceragioli/Berry
show in their book that better correction within the basic design is
possible, including flat field, but something is left to be desired: the objective's image is
almost touching the field lens surface, and the eye relief is only ~18%
of the focal length (the book puts it at 22%, but it would require a very
short focal length objective, binocular-alike); also, lens size limits the field
at 20° radius even with f/10 beams. Design shown here under #3
(0/5/-5/10/0mm radii, 0.5/1.9/1.4 lens thicknesses, 8.9mm separation
with F2/BK7/BK7 glasses from left to right) has
about 50% larger lateral color error, requires little over 2.5 diopters
field-edge accommodation, and has about a third more of astigmatism,
but offers round spot plots, lens surface safely away from the objective's image,
and 3mm of eye relief at 20° off. It also can accomodate field up to
45° in diameter. It could also be made flat-field, with nearly identical
level of aberrations to that in the S/C/B, and 4mm eye relief, by weakening the field lens to 12mm,
and increasing thickness of the 2nd element of the eye lens to 2.4mm (most of the
reduction in positive astigmatism).
Small changes to the basic configuration allow
yet better correction, as shown with the "modified Kellner" under #4. The
lenses are significantly closer, allowing for longer eye relief, astigmatism
further reduced, and required accommodation at 20° is less than -2.5
diopters. The astigmatism reduction is achieved by bending the rear eye lens surface,
and making the rear surface of the field lens concave took care of the
lateral color. Another way of achieving lateral color correction is to make
the cemented surface somewhat more strongly curved. Other modification are
also possible, and such modified Kellner can have significantly better
performance than its old fashioned cousins.
The true Monocentric is eyepiece design dating back to the
19th century, when it was invented by Adolf Steinheil (1883). As its
name implies, its surfaces are concentric about a common center of curvature.
In the form, it is a cemented triplet with the crown element sendwiched
between two flint elements. The original version by Steinheil wasn't symmetrical,
and some others,
like that by Philip Taylor (US Pat. 2,604,012, 1952) were. Taylor's version
had very good correction over ~25° field diameter at f/10, with acceptable
edge accommodation of about -2.5 diopters (10mm f.l. unit). The monocentric
shown here (5.85/2.75/-2.75/-5.85 radii, 3.1/5.5/3.1mm thicknesses,
F2/BK7/F2 from left to right) is symmetrical, with 4.2mm eye relief,
exceptional correction over most of the field and somewhat demanding
edge accommodation of over -3 diopters required. Its high field correction
is based on a delicate balance between lower and higher order astigmatism
(generated by the two inner radii), which can hold within a relatively
small field. The curvature can be significantly lessened by a small
strengthening of the inner radii, but at a price of more astigmatism
in the wider edge area. Also, correction can be somewhat improved by
making design asymmetrical. This design is only of historical significance,
since similar and better performance now can be achieved with less
glass (modern "monocentrics").
The modern "monocentric" shown here - same as the one in "comparative
raytracing" - is a cemented triplet made of three different glasses. It
achieves better correction than the symmetrical true monocentric, and has significantly
longer eye relief of 7.2mm. Required edge accommodation is also lower at
-2.3 diopters. It should be noted that the 15° ray spot plots for
these eyepieces are given for their optimum location, different than that
for the 0.7 field spots; by default, best astigmatic image is midway between
the sagittal and tangential surface. In general, since their astigmatic field curls back
due to the higher-order astigmatism, edge points require less accommodation.
When comparing the commercially available Steinheil and Hastings
triplets, they have somewhat smaller quality field of about 25° in
diameter, exception being the Edmund Scientific Hastings, whose 12.5mm
unit has somewhat worse edge correction with 30° field than this triplet,
but significantly lower edge
accomodation of little over +3 diopters required (when downscaled to 10mm,
as opposed to +10 and more
required by ES Steinheil, and Thor Labs units). It is not that the other three
are poor designs, it's about different design priorities. The three narrower
field eyepieces have zero-accommodation flat field up to 10-12°,
and are paying for it with more astigmatism beyond that point. The ES Hastings
has a curved field with the accommodation required reaching maximum of -2.6 diopters
at about 0.7-0.8 of the field radius. It's a common trade off in
accepting some field curvature for better edge performance.
The last design in this group (#7), that could be called simplecentric,
is a cemented doublet (10/-3.8/-7.9mm radii,
3.1/1.3mm thicknesses, N-SK11, SF1 from left to right), with its correction
level approaching that of the triplet. In fact, by changing the second radius
to -3.85mm, correction becomes nearly identical. With the required edge
accomodation of less than -2 diopters, and only two glass elements, it is a
viable option to the cemented triplets.
40°-55° FIELD EYEPIECES
These are 2+1, 2+2 and 3+1 designs (3+2 variations, like Jean Cojan. They can be looked at as more advanced
vs. previous group, in that better correction of aberrations allowed for
wider corrected fields. The simplest Koenig, 2+1, in its original patented
form had planoconvex eye lens, more of a lens separation (3.4mm at 10mm f.l.),
no more than 45° usable field (with +5 diopters
accommodation required at that field radius), over 2.5 waves P-V of astigmatism
at the field edge, and lateral color unacceptable by today's standards.
Rutten and Venrooij improved somewhat on this original design, but
according to what seemed to be their policy, not to extent that its
performance would radically change; it amounted to slightly less field
curvature and (significantly) better lateral color correction. More radical versions,
such is the one shown below, have significantly better overall
correction, allowing fields in excess of 50° (for comparison, at 25°
radius astigmatism is only 1 wave P-V). This particular design
requires much less of a much easier for the eye to handle, negative accommodation
at 25° field. It also has a peculiar astigmatic field, with the balance
between lower and higher order astigmatism resulting in a practically astigmatism-free
half-field.
According to its manufacturer, Edmund Scientific, RKE acronim should
contain names "Rank, Kaspereit, Erfle", the first
for its designer, David Rank, and the other two for no obvious
reason. Its configuration is nearly identical to the Koenig 2+1,
and seems the purpose of throwing in Kaspereit (2+2+2) and Erfle (2+1+2)
was to divert from that fact. "Reversed Kellner", or the initial name for it by
the ES, "Rank Kellner eyepiece" would be certainly more
appropriate. It
was designed back in the 1970s for Edmund's Scientific 105mm f/4.2
Astroscan. Shown is the 28mm unit scaled down to 10mm f.l. Similarity in
the lens arrangement to the 2+1 Koenig extends to the similarity in performance level.
According to the Smith/Ceragioli/Berry (p499), the original design by Simon
Plossl was actually achromatized Ramsden, i.e. a pair of widely
separated positive achromats. It was Albert Koenig who brought the
two achromats together and created the basic form of what we today
call "Plossl eyepiece" (USP#2,217,281 Jan. 1939). Koenig himself
called it "orthoscopic according to Plossl", and that is probably how
it got to be called "Plossl". Koenig's "Plossl" was asymmetrical,
using three different glasses (crown for the two inner elements,
ordinary and heavy flint for the outer). It has good overall correction,
but lateral color correction leaves something to be desired.
The Plossl shown here is based on the patent prescription of
Albert Nagler. Correction level is similar to the previous two designs,
with the advantage being less of field edge accommodation required:
-1.25 diopters, low enough to make it practically flat-field visually.
The symmetrical eyepiece is just a form of the symmetrical Plossl.
Astigmatism could be reduced to the level of the Nagler Plossl, if traded
for acceptable field curvature (-2.5 diopters).
Clave Plossl is, according to Chris Lord, the above mentioned patented
design of Albert Koenig (US#2,217,281), which was only produced under Clave's name.
Smith/Ceragioli/Berry state that it is a post WW2 design
by Maurice Paul. However, an
article
in French says it was Jean Texereau himself who
modified the eyepiece, while Marcel Paul Clave and Serge-Rene Clave
designed the Clave Barlow. Since no prescription for Clave Plossl was
published, we'll show the Koenig's design, modified to two glasses
mainly to minimize lateral color error (they are similar
to some extent, with drawings on another French
site suggesting that
the true Clave had flat outside radii, with somewhat asymmetrical
elements' radii and thicknesses). It is asymmetrical Plossl, a flat-field design with good edge correction and some
residual coma. Since coma increases with the 3rd power of focal
ratio, and astigmatism with the 2nd, it is more noticeable at f/5.
It has lower distortion than other designs in this group. Note that
flattening the other outer radius would require use of different
glasses - Schott SK2 and SF1 would do a good job - but the output
would remain practically identical (small differences in thickness
don't produce appreciable effect).
The Brandon eyepiece is, according to Chris Lord, reversed
Clave Plossl. The similarity is there, in both, lens arrangement and
output. Exact prescription is not known, only that it uses four
different glasses (this arrangement uses SF1/PSK3-SK5/SF10, from
left to right). There is no effect from making the field
lens significantly thicker, other than a small (10-15%) reduction
in the astigmatism/field curvature. Residual coma is probably what
makes these two designs less suitable for fast focal ratios than
designs without it (as the diffraction images show, coma transforms
roundish astigmatic image into a triangular shape with a bright, curved
base).
Well regarded for its correction, Abbe orthoscopic
eyepiece is usually tought of as confined to somewhat smaller fields.
This design is no different in configuration than another patented Koenig
design (same patent number as for his Plossl), which could
be more advanced than Abbe's (will never know, since there is
no known prescription, but Abbe's design was limited to 30° field).
Unlike the Koenig's patent, the design shown uses
only two different glasses, since it is all that's needed
(the patent used barium dense flint - BASF64 or alike - for
the eye lens, which is a high-index low-dispersion glass, close
to some lanthanoids, now advertised by Zeiss Jena as being
used in their Abbe orthoscopic eyepieces).
As raytrace shows, its field correction can be just as good as that of
other designs in this group, with its nearly flat field as added bonus.
If desired, astigmatism can be traded for field curvature, and if the
ultimate in correction is pursued, field can be somewhat reduced, to
stay within acceptable field edge accommodation requirements. Such a
design, H-ortho (from "highly orthoscopic") is shown under #8.
Its correction remains unbelieveably good even at f/5, with the central
diffraction maxima nearly intact at 20° off axis. The price to pay
for it is -3.5 diopters edge accommodation required, which would be
too much for some people. A very similar design, but using expensive,
ultra-high-index glasses, is Janeczko et al. (from US 7,804,651B2, 2010),
designed for night vision goggle systems and head mounted displays.
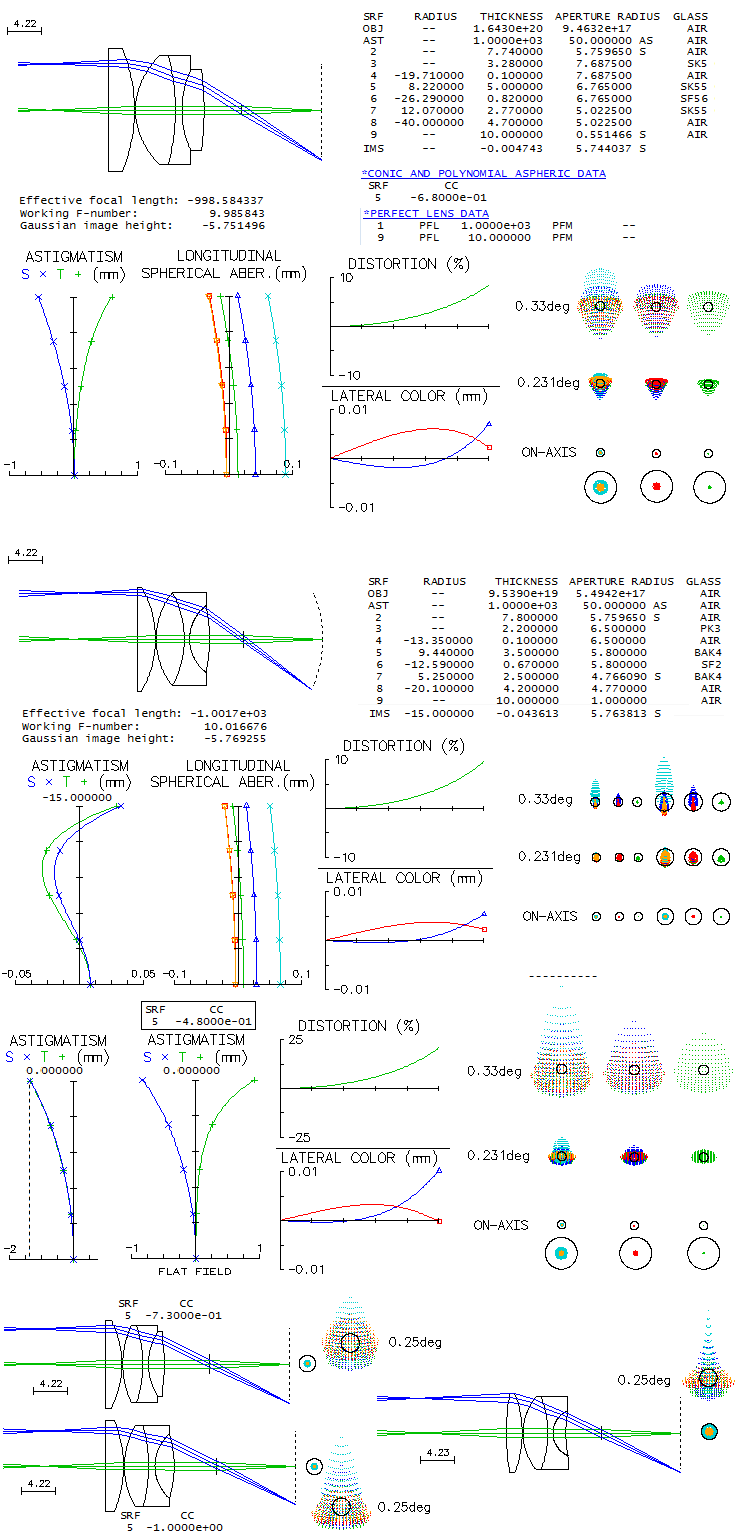
Yet another variation on the singlet+triplet
form is Richter eyepiece, with one surface aspherized. The main
difference with respect to Abbe is that the 3rd and last radius are considerably
more strongly curved (similarly to the Abbe, the Richter is developed
within the Zeiss company). This particular arrangement is a microscope
variety, with the last surface concave and - to compensate for it -
biconvex field lens. With no
prescription found, it can be reconstructed from what appears to be
accurate drawing of the design. One such reconstruction is
raytraced below. Starting point for the glasses were those specified
for the wide-angle inverse Richter eyepiece, which worked well, except
that SF10 is replaced by SF2, as required to minimize lateral color
error. The glasses are asigned to the elements based on best
overall performance (different order tends to produce more curved field).
Unit focal length is also 10mm, this time in direct raytracing, with
OSLO "perfect lens" as objective and eyepiece. True angular field
of 0.252° corresponds to 25° AFOV radius (the 2nd surface is a
dummy surface placed at the front perfect lens focus, hence the
"aperture radius" value for it represents Gaussian image radius at the
focus of the objective).
With the radii closely conforming to those of the drawing, the
astigmatic field is moderately curved, with the outer field becoming
less curved due to the rapid increase in higher order astigmatism
of the same sign (top). At -40mm field curvature radius, approximately
midway between the edge and 70% zone foci, uneven astigmatic field
makes required accommodation vary from
negative at the 70% zone (-2.5 diopters), to positive (about
+2.5 diopters at the edge). While neither alone is exessive, the
combined differential of 5 diopters would be challenging for more than
a few people. Color correction is good, particularly
lateral color correction. Astigmatism can be reduced, with stronger
field curvature, or increased to flatten the field. Magnitude wise,
it is similar to that in the Abbe shown. Although cited aspherization
calls for a parabolic surface 5, it would add far too much astigmatism
and (positive) field curvature. As small as -0.02 conic flattens the
field adding quite moderately to the eyepiece astigmatism; no other
aberrations are significantly affected.
With relatively small changes in the radii, and the other parameters
unchanged, better overall performance can be achieved (bottom). Best
field is somewhat more curved, but accommodation changes evenly with
the field height, and edge accommodation is still acceptable at -5.5
diopters. Needed aspheric to flatten the field is -0.09, still quite
low, indicating that flat field could be also achieved with generally
small changes in the design. The slight
curl inside on the top of the tangential plot is due to the higher order astigmatism
of opposite side. It leads to astigmatism decrease for higher field
radii, where at some point T and S plots cross and astigmatism (of
opposite sign) again starts to increase. This particular design would
have good field quality at f/10 up to 65-70° AFOV, but required
accommodation due to field curvature would become prohibitively high.
Redesigning by allowing somewhat more of astigmatism for
acceptably curved field is possible, giving to this
configuration a wide-field potential.
55°-65° DESIGNS
The simplest Bertele is 1+1+2 arrangement. Its original patent design from 1925.
(US pat. 1,699,682) claims up to 70° field diameter, but by today's standard is nowhere
close to it. When scaled down to 10mm f.l., at 33° off axis it generates
3.4 waves P-V wavefront error of astigmatism (5.5 times the Airy disc),
on its best image surface which have 21mm radius, convex toward the eye.
This means that the eye has to relax nearly 9 diopters beyond its infinity
mode to focus onto it, after being focused on the field center (it is like
accommodating from infinity to a 12cm distant object). In other words, field
center and perifery can't be in focus at the same time, with the latter
requiring action by the focuser. On top of that, lateral color error
limits sufficiently corrected field to little more than 10° radius.
It illustrates well the limitations imposed by the lack of available
glasses and by today's standard primitive designing means (lateral
color error can be reduced to negligible if the original SK7/SK7/FK5/SF2
sequence is replaced by FK5/FK5/FK5/SF10). Nearly identical lens-shape wise
arrangement could indeed be stretched out to a 75-degree field, or so,
with the worst error of 1.5 waves of astigmatism at the 0.7 zone, and
better than "diffraction limited" at the edge -
really accomplishment, considering its simplicity - but still with more
than 3 diopters of beyond-infinity accommodation between the center/edge
and 0.7 zone required. The modified Bertele shown here still
maintans nearly identical original design, but with somewhat different
glasses and lens surface radii, resulting in a more favorable form of
astigmatic field. The ray spot plots are for the best focus location,
by definition midway between the tangential and sagittal surface (it
may vary somewhat in the presence of significant higher-order astigmatism,
or other aberrations), so that the approximate accommodation required
can be determined from the graph. In this particular design, the outer
~15% of the field radius require divergent (natural) accommodation,
maxing out at nearly -2.5 diopters at the edge (vertical dashed line)
and most of the rest of the field require convergent (beyond infinity)
accommodation up to 1.5 diopter. Not eye-friendly, but significantly less
so than the original design. Using other common glasses the beyond-infinity
accommodation can be entirely eliminated. Lateral color is well controlled, but due to
design simplicity, longitudinal chromatism can't be at the same time (unlike
the original design, which has entirely negligible axial color, at the
expense of unacceptable lateral).
The error is larger in the blue/violet, 0.25 wave in the F-line, and 0.7
waves in g-line (436nm) at f/10. It can be somewhat reduced - down to
0.17 waves in F, and 0.45 in g, possibly more - but for
a complete correction the field lens needs too be achromatized
as well. Negative (barrel) distortion is near 18%.
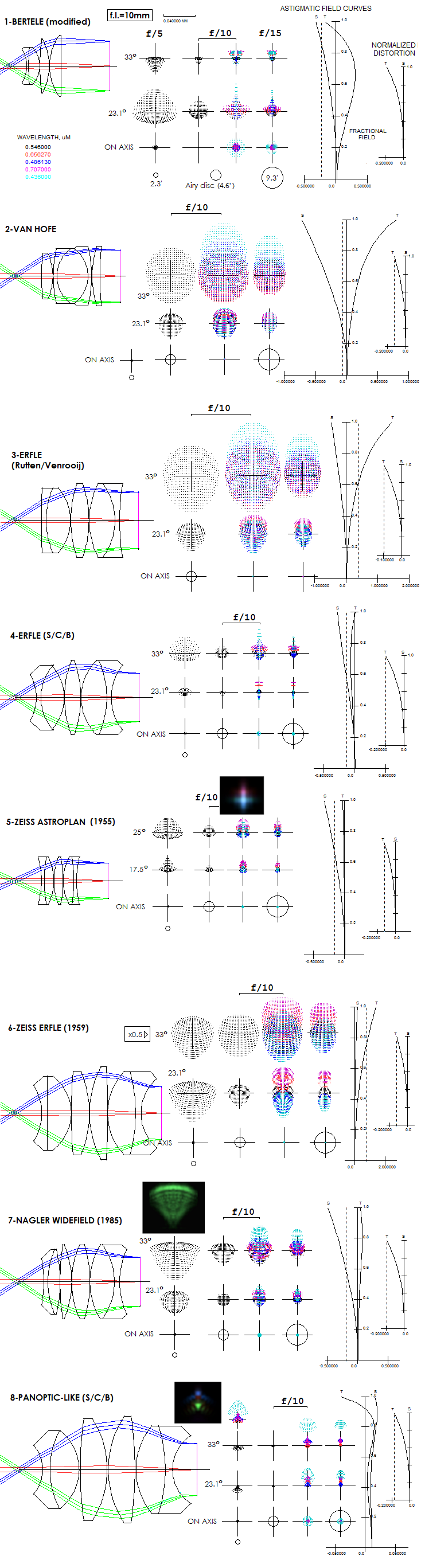
Similarly to the Bertele, the original Van Hofe design from 1924.
(US pat.1,759,529) had unacceptably large lateral color error, although
somewhat lower astigmatism and less curved convex-to-eye field (the original design,
which proposes somewhat longer eye relief, that would correspond to a very
short-focal-length objective, had a flat field). Modification shown here
uses the same glasses, in the same order, except that the eye lens is
PSK2 instead of SK6, biconvex (planoconvex in the original), and with
the central element made thinner, but with more strongly curved radii.
Lateral color is corrected, except the field edge, edge astigmatism about 10% larger, and the inner
field astigmatism about 20% lower. Best image field is practically flat.
Created with the idea of an expanded-view monocentric, the Hofe eyepiece
achieved wider field, but there is no comparison correction wise.
For decades, the Erfle was the synonym for a widefield astronomical eyepiece.
The original 2+1+2 design from 1921. (US pat. 1,478,704) like nearly all
old designs was poorly corrected by today's standards. Somewhat modified
Erfle presented by Rutten and Venrooij had significantly less of lateral
color and astigmatism/field curvature than the original, but not so much as
to lose a connection to it. At f/10, the edge astigmatism (33° radius) is 3 waves P-V,
required field-edge accommodation is still over 3.5 diopters. Distortion is
relatively low, nearly 10%. By further weakening of the two radii contributing
most of astigmatism, and changing glasses as necessary for color correction,
the field can be flattened, with the astigmatism reduced to less than 2.4 waves
P-V. Continuing in the same direction, reduction in astigmatism is traded
for the increasing field curvature, and the near-optimum balance is given by
the "modern Erfle" from Smith/Ceragioli/Berry. Its lateral color peaks
at 0.7 field radius, where is nominally acceptable (F and C lines separated by less
than Airy disc diameter), but with the blue inside Airy disc, and both red lines
outside of it. Distortion is significantly greater,
at 20%. Maximum accommodation required is about -1.5 diopter (diverging),
much easier to the eye than up to a few times higher converging accommodation
of the old-style designs. Similar to Erfle, 2+2+2 (three achromats) arrangement,
known as Kaspereit eyepiece (1923), allows for better lateral color
correction; this was more significant back in the day when glass selection
was limited.
Zeiss Astroplan was apparently an attempt to adopt Erfle design to a smaller field.
It allowed for considerably smaller size and a cleaner field. Although used
for AFOV up to 50°, by design it is a widefield eyepiece and more comparable
to designs from that group. Astigmatism is
somewhat lower than in the designs usually employed for that field size,
not very much, but enough to have smaller blur at 25° than Nagler
Widefield at 23°.
Laterall color error at the field edge is nearly non-existent in the blue/violet
(according to SYNOPSYS; according to OSLO Edu it is roughly half of that in the red),
while the two red lines are somewhat overcorrected (as illustrated on the
diffraction image, with even sensitivity). Maximum accommodation required,
at the edge, is -1.6 diopters, much friendlier to the eye than the full-blown
Erfles from that era. Note that the original Zeiss design had different
mode of correction, with some negative (tip up) coma left in, somewhat lower field edge error
but nearly by a third stronger field curvature, better lateral color
correction except for the violet, which is worse. A simplified version,
using SK2 for the three inner elements, and SF4 for the two outer elements,
would have the best overall correction, but the differences remain small.
Zeiss Erfle from 1959, as presented by the Gross' Handbook (most prescriptions there should be
accurate, but there are some errors; that for the 1+1+2 Bertele is unusable)
is quite massive eyepiece for that time, with the outer field correction
leaving something to be desired. Lateral color is worse on the red end
(overcorrected), nominally nearly constant thru the outer field, hence
the worst around 0.7 zone, where the blur is half as large as at the
edge. It requires +4 diopters edge accommodation,
which means the only way to focus on it is to refocus mechanically. It is
unsuitable for fast focal ratios: at f/5, its astigmatic blur at the field edge
has angular size of the full Moon. It is possible it was designed
for some partly compensating arrangement.
Coming in the same 2+1+1+2 configuration as the Zeiss Erfle, the Nagler
Widefield brings significant improvements in the overall correction. Its
astigmatism at 33° is only marginally higher than that of the Zeiss at
23°, hence nearly cut in half. Its lateral color correction is very good,
with the partial exception of the violet toward field edge. Its field
edge requires -2 diopters of accommodation - i.e. as from infinity to
0.5m - easy enough for most people. It, however, has relatively high
distortion and some coma, negligible
at slower focal ratios, but becoming visible at the fast ones, making
diffraction blur asymmetric. Since astigmatism between aprox. 0.5-1 wave
P-V wavefront error (about 1-2 Airy discs in diameter) at sufficient
magnifications shows as a little cross, it would in the Widefield have
that kind of deformation at about 10°-15° off axis, quite close
to the midfield. I read somewhere that it was these little crosses that
prompted Al Nagler to come up with something better: the Panoptic.
There is no published prescription for the Panoptic, but the
design from S/C/B should illustrate well its level of correction.
Astigmatism is practically non-exsistent, except at the field edge, with
the longitudinal aberration of ~0.06mm at the very edge implying ~0.5 wave
P-V (divided by 8F2, same as for defocus), or ~0.1 wave RMS.
Dominant aberration is trefoil (which doesn't show on the astigmatism plot),
but even at the field edge the central diffraction maxima is still intact,
with 0.45 Strehl (0.56 at the 0.7 radius). The only part of the image that
deviates from excellent is axial and lateral color error un the violet, but it has
generally little importance (axial blur at f/5 is twice the blur at f/10, or
little over 1.5 wave P-V wavefront error).
All previous designes were all-spherical, except the Richter microscope
eyepiece above, which in the reconstruction attempt required very mild
aspherization. An older aspheric design
presented on Peter Smith's page (US Pat. #1,968,222 by
Robert Richter, 1933) was intended for 65° AFOV. It is the same
1+3 arrangement as for the Richter microscope eyepiece in the previous
group, but the field lens is now plano-concave, and the last surface
is convex. No prescription is given, nor could be found online, so
here is a reconstruction based on the raytrace drawing given on the
page, with the starting glasses same as those for the microscope variety
(change in the glasses is needed mainly for minimizing the lateral
color error after the other aberrations are minimized by bending the
radii and changing element's thickness). Unlike the group above,
used is direct raytracing, with OSLO "perfect lens" as objective
and eye lens. The 0.33° field angle corresponds to 65° AFOV
(with ~8% positive distortion; design in the middle has as much as
+20% distortion after aspherization, thus producing 72° AFOV
with the same 0.33° field angle at the objective).
The original design (top) features a strongly curved 3rd surface, having as a
result some low residual coma (coma contribution of the 3rd
surface cannot be better offset by those of the other surfaces).
Astigmatism-wise, it is midway between Zeiss Erfle and Nagler Widefield,
but having color correction and field flatness nearly as good as the latter.
Coma residual can be lowered by making the 3rd surface less strongly
curved (middle). This configuration is made astigmatism-free when all-spherical,
to illustrate the
effect of aspherization for the purpose of field flattening. The first
astigmatism plot shows astigmatic surface around -15mm field radius;
below is the same vs. flat field, when the required edge accommodation
is over 13 diopters. Putting -0.48 conic on the 5th surface (3rd
surface of the eyepiece) flattens the field, by inducing needed
amount of astigmatism. It results in a considerable increase in distortion,
and have a relatively small effect on lateral color (increasing red vs.
blue distortion). On the bottom are three variations of the arrangement
illustrating that the conic can be varied from 0 to -1 without significant
change in flat-field performance. The all-spherical configuration (right)
has somewhat lower astigmatism, but more of longitudinal chromatism
(it does not necessarily mean that it couldn't be improved in that
respect, but if it could, it would require more
involved re-designing). Note that these last three designs, while also
10mm f.l. at f/10, have smaller
field and a different Airy disc scale.
Inverted configuration (1+3) was patented by Richter (Zeiss) as far
back as 1932 as 82°
8.9% distortion eyepiece. There is no prescription available,
but it can be assumed that this wide field coupled with low distortion
was probably paid for with compromised astigmatism/field curvature and/or lateral
color. This simple configuration does not allow for minimizing all
aberrations at the same time; if it would, we wouldn't need the much more
complex Smyth lens designs of the modern day.
An example of aspheric eyepiece with a nearly complete prescription given
is the 60° AFOV design by Seymour Rosin and three other NASA employees
(Wide angle long eye relief eyepiece, US Pat.#3,472,577 1969).
It is a 3+1 arrangement with the strongly curved singlet surface aspherized.
Patent states that the singlet does correction of monochromatic
aberrations, with the zero-power triplet correcting for lateral
color. It also points to the presence of coma, due to which it is not
recommended to use exit pupils larger than 5mm (since the patent unit f.l.
is 50.5mm, it implies f/10 cone, or slower; coma changes with the third
power of focal ratio, hence it is eight times larger at f/5 than
at f/10). As all other eyepieces on this page, the patent unit is scaled down to
10mm focal length. Surface conic in patent prescription is
defined by the sagitta depth, but since no corresponding lens diameter
is specified, it is somewhat speculative. However, raytrace shows that
it is most likely approximately paraboloidal. Presented are both,
reverse (top) and direct raytrace (bottom) of this design; the
differences are not negligible.
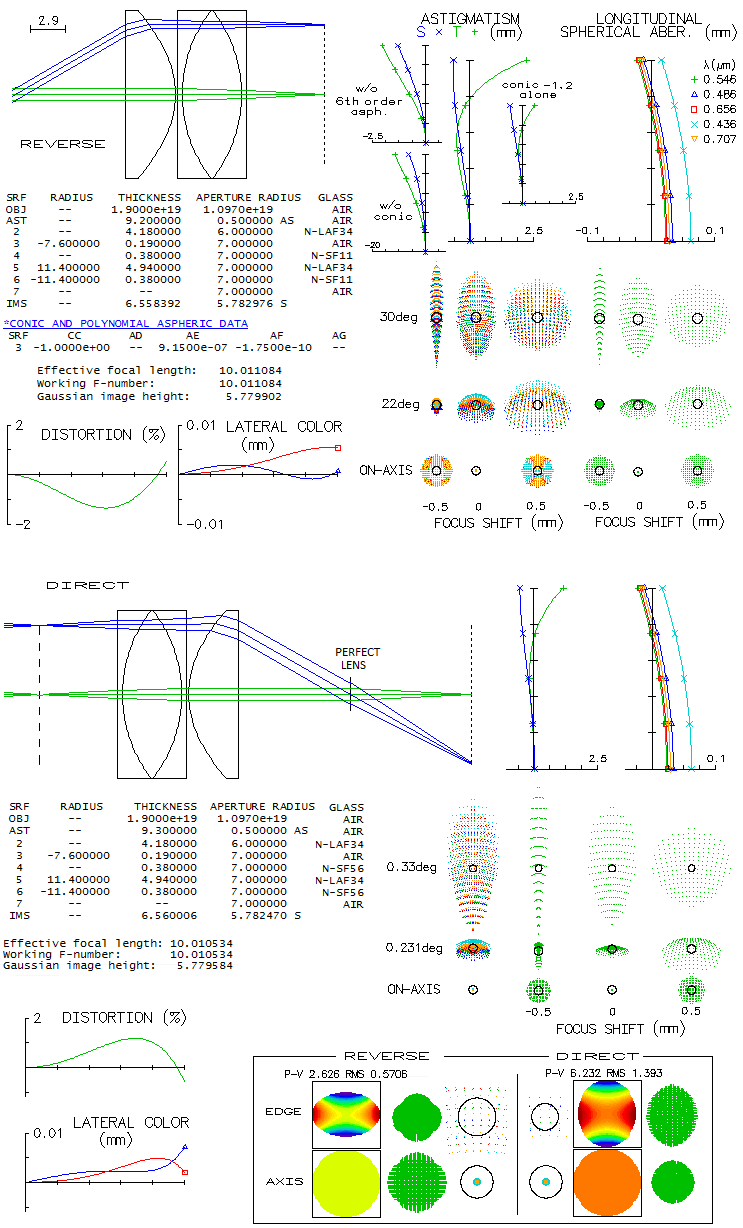
The astigmatism plots with reversed raytracing show the effect of
aspherization. With surface #3 left spherical, both astigmatism and
field curvature are prohibitively strong. With -1 conic alone, both
are greatly reduced, but field curvature is still far from acceptable
(roughly 15 diopters accommodation for field edge). Given 6th order
coefficient nearly flattens the field, at a price of significantly
larger field edge astigmatism. Given 8th order coefficient is too low
to have appreciable effect; it would significantly reduce edge astigmatism
if nearly a dozen times higher. Overall correction would have been
similar with -1.2 conic alone, but adding the 6th order term as the
prescription calls for would produce unacceptably strong astigmatism
and field curvature. Color correction is excellent, and distortion
near negligible (note that the glasses in pattent application are given by
the inde and Abbe#, nearly matched by closest contemporary glasses
for raytracing purpose).
Direct raytracing uses "perfect lens" for the objective and the
eye. It gives very similar output in the form of astigmatic field,
but not in the magnitude. What is particularly puzzling, is that
longitudinal astigmatism for field edge point is nearly 40% smaller,
but the corresponding P-V error is nearly two and a half times
larger. Taking a closer look reveals that the Airy disc presented
by raytrace is significntly smaller for the edge point than on axis,
and more so compared to the edge point Airy disc in the reverse
raytracing, which is larger than the axial disc (bottom, boxed).
Since distortion is negligible, most likely cause for this discrepancy
is the way raytracing software processes width of the cone coming out
of the eyepiece. Shown are wavefront, footprint shape on the singlet's
flat surface, and Airy discs displayed (footprint shape in the reverse
raytracing given by OSLO Edu has a peculiar shape of two elongated shapes overlaping
perpendicularly, even on axis, indicating a software glitch).
Apparently, cone width is
measured vertically along the wavefront, hence
the field edge Airy disc is smaller in direct raytracing, and larger
in the reverse. In effect, it makes the former f/11.5, and the latter
f/8.2 (approx.), with the P-V wavefront error differential for any given nominal
longitudinal astigmatism being about two times. This explains a
better part of the astigmatism contradiction; the rest is probably due to
seemingly common differences in how astigmatism generates in
reverse vs. direct raytracing. Main reason for the inequality is that
reverse raytracing assumes identical pencil width at the pupil,
which is in practice valid only for small field angles.
The wavefront elongation due to the cone width deformation at large
field angles does affect diffraction image. In effect, it reshapes the
aperture correspondingly, with the shorter diameter producing wider
image than the longer one. It is not noticeabe in this case, due to
the large magnitude of astigmatism, but SYNOPSYS offers as an option
aberration-free diffraction image for any field point (below).
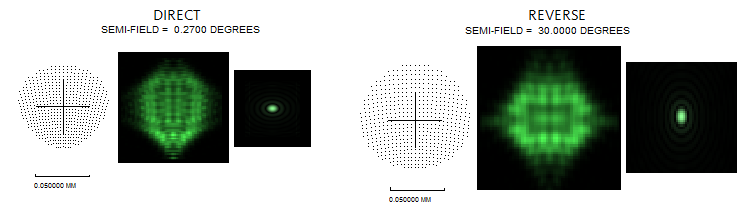
Other than differences in the spot size (left) and actual diffraction
image (middle), it shows that the aberration-free
diffraction images for the edge point (right) are indeed elongated, as expected
(field angle in direct raytracing here is smaller than in OSLO because
SYNOPSYS doesn't have "perfect lens" feature, and the aberration-free
system used to simulate it has 1200mm f.l. vs. 1000mm for the "perfect lens
in OSLO).
~70° AND OVER
There is no official field size at which the extra-wide fields
begin, but considering that traditional wide-angle eyepieces -
or at least those that were in practical use - generally remained
below 70° field diameter, that could be viewed as the dividing
level. The first design that boldly made a step
over this line, into new generation of exceptionally well corrected
extra wide-fields was the 1981 Nagler, known as Nagler 1. Below
is the Nagler 1 design "a" in Al Nagler's patent application. It
will be singled out here to illustrate some specifics related to
this class of eyepieces. The #1 is so called Smyth lens,
a negative lens acting as tele-extender (Barlow) some distance
in front of the objective's focal plane. It changes geometry of
rays entering the following it, positive lens group in that they are
now spreading wider, and more so toward the field edge. This requires
larger, more strongly curved lenses. It makes possible
to achieve lens combination which will have compensatory action
on field astigmatism over a significantly larger radius, up to a
point when higher order aberratios spring out of control. The Smyth
lens alone is not enough, as the Koehler 110° eyepiece illustrates.
But this design acrobatics comes at a price: light cones traveling through
different lens areas, of very different curvatures, tend to exit
the positive group differently - the parallel pencils exiting the
eye lens from the outer cones, passing through
more strongly curved part of lens surfaces, tend to intersect
optical axis closer to the eye lens than the pencils from inner-field cones.
That is known as spherical aberration of the exit pupil, with
the exiting parallel pencils not intersecting the axis nearly at the
same location, forming a tight exit pupil, but rather extending pupil
erea longitudinally.
If excessive, it can cause darkening of the outer field areas, the
"kidney bean effect". Conventional eyepieces also have spherical aberration
of the exit pupil, but generally smaller, inconsequential. It is
more likely to be noticed in the extra-wide field designs, and it makes it
their #2 specific.
In raytracing, this exit pupil disarray makes impossible to accurately
raytrace such eyepiece from a fixed exit pupil location. Picture below
(bottom) shows how different, grossly inaccurate astigmatic field becomes in field areas
with different exit pupil locations. This, of course, means just as
inaccurate ray spot plots. For accurate output, every narrow zone needs
to be raytraced from its appropriate exit pupil location, so that the
entance beam on the other side is only midly converging toward optical axis.
For that reason, a standard raytracing software can't produce a single
accurate astigmatic field of such eyepiece: it has to be pieced together
from separately raytraced different zones. So the first plot from left,
showing astigmatic field generated when raytracing from the exit pupil
for the field edge, has that pieced up real astigmatic field as the
redish area around vertical axis (approximately). The rest of plots, from
left to right, show astigmatic plots for exit pupil of the 0.8, 0.6, 0.4
and 0.2 zone, with the corresponding exit pupil locations (ER is eye relief, the exit pupil
separation from the eye lens). The rightmost plot shows astigmatic field for the entire
40-degree radius when raytraced from the midfield exit pupil: the more
distant entrance pushes the outer light cones farther toward lens perifery, and
the non-existing astigmatism jumps of the chart for the outer zones.
Nagler 1981a is a 10mm f.l. unit, and it is shown for f/10 entry cone.
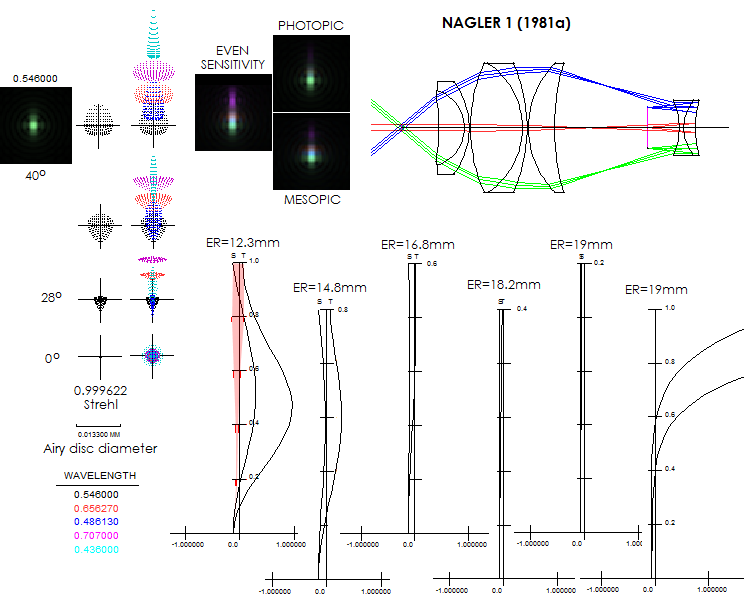
The field is for all practical purposes flat, with the required
accommodation remaining below 1 diopter. The actual ray spot plots (left) show that at f/10 even the very
edge still preserves the central diffraction maxima (the e-line blur
is about 0.7 the Airy disc diameter, implying about 0.085 wave RMS wavefront
error). Lateral color is well corrected for the blue/violet in the inner
field, with the violet flying off toward field edge, while the red
end splits off higher in both, midfield and edge. Field edge shows significant
lateral color, looking incospicious in the photopic mode, but becomes fairly
obvious in the more likely for night time observing, mesopic mode
(as a reminder, lateral color doesn't change nominally with the F-ratio,
which means it is twice as bad at f/5, due to the twice smaller Airy disc).
Another example is Nagler 1981b, which was omitted above, but is
interesting because it's nearly 1/3 smaller than Nagler 1981a. It
also has one extra element, being 2+2+2+2 configuration, which
helps in better control of the lateral color error.
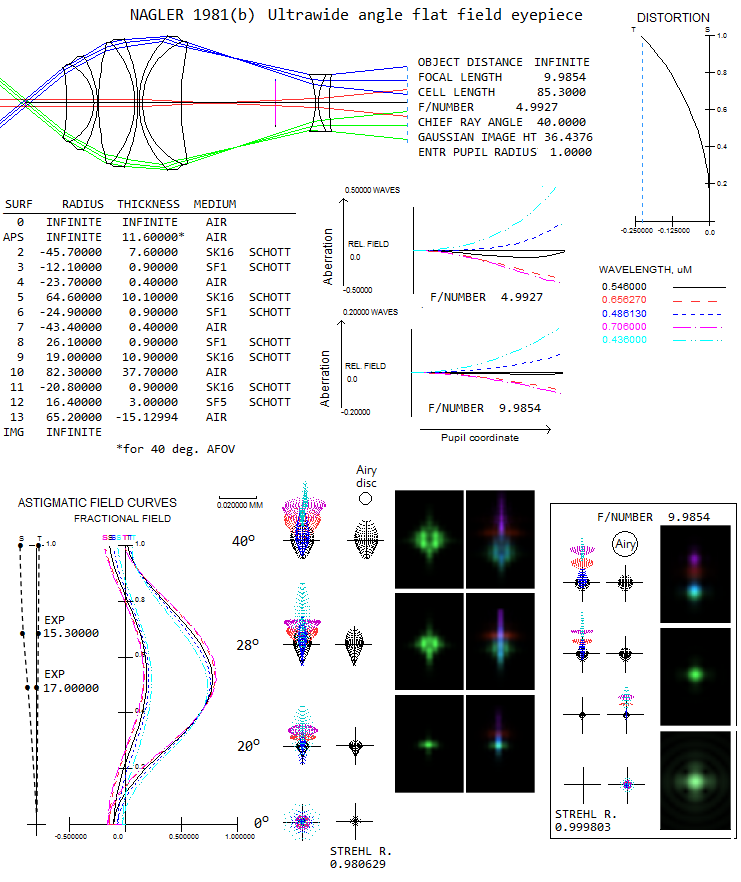
It has noticeably more astigmatism toward outer field, which could
become noticeable at fast focal ratios. Longitudinal chromatism is
very low, but at f/5 wouldn't satisfie the "true apo" criterion (not
by much). Similarly to the 1981a, its true astigmatic field
(botom leftmost, for e-line alone) is
very different than that obtained for the fixed exit pupil location
(the one for 40° field angle, next to it). Distortion exceeds -20% (since
it is reverse raytracing, actual distortion is positive in sign,
stretching the image bigger). All aberrations except lateral color
are much lower at f/10 (bottom right; diffraction images are only
for 40° angle, with e-line pattern shown for linear and logarithmic
response).
Since the Koehler 110° spot plots are large enough, this time will
start with another interesting design from the pre-Nagler era: the Ludewig
90° eyepiece from 1953 (US Pat.#2,637,245). It could be looked at as
a transitional form between conventional and new Smyth-lens designs, in that
it does employ a negative field lens, but it is placed right next to the
positive lens group (in this arrangement, separating the negative lens
worsens the lateral color, this is why it is "glued" to the next lens).
Although Ludewig claimed fields of up to 90°, it is shown only for
80° field, since astigmatism already becomes objectionable. At 80°
the mainly astigmatic blur (with some residual coma) is over 5 Airy disc
diameters, which translates to more than 3 waves P-V wavefront error (over 0.6
waves RMS). Since the green f/10 Airy disc in a 10mm f.l eyepiece
is 4.6 arc minutes wide, it corresponds to some 25' apparent diameter.
It is still better than the traditional Erfle, which would, even in the
improved version given by Rutten and Venrooij, have about 50% larger blur.
However, required field edge accommodation to the best focus is over +11 diopters,
which means that most people would focus closer to the elongated,
line-like sagittal focus (more so considering the difficulty of focusing
beyond-infinity). Lateral color error has a reversal at about 70% zone,
diminishing somewhat toward the edge, but remaining unacceptably large
in the outer field. Distortion is surprisingly small for this field size,
and the exit pupil shift is negligible. With today's raytracing software,
the design can be improved to a nearly flat-field, with about 50%
lower astigmatism and significantly less lateral color (below; the
defocused field shows about -1 diopter required for the field edge,
and about half as much for the 0.7 zone). Similar configuration has been
patented in 1998 as a 65° design (Koizumi/Watanabe, Fujinon Corp. #6,069,750;
this design has nearly identical configuration to the William Optics'
SWAN, and likely was the basis for that series).
Note that unlike the rest of designs in this group, this one is given
for f/10 and f/15 beams, with the raytrace illustration for f/10 (1mm exit pupil); it
means that it is shown twice larger relative to the others.
Another design can be interesting as a transitional form, even
if it is relatively recent. It is a 80° AFOV 5-element Erfle with 2-element
Smyth lens configuration by Imaizumi. In its patent application it is
given as a part of the system with the objective and thick prisms,
so it needed to be a bit modified for stand-alone performance. It
should be somewhat better if optimized, but even without it performs
significantly better than the comparable (flat-field) 5-element Erfle.
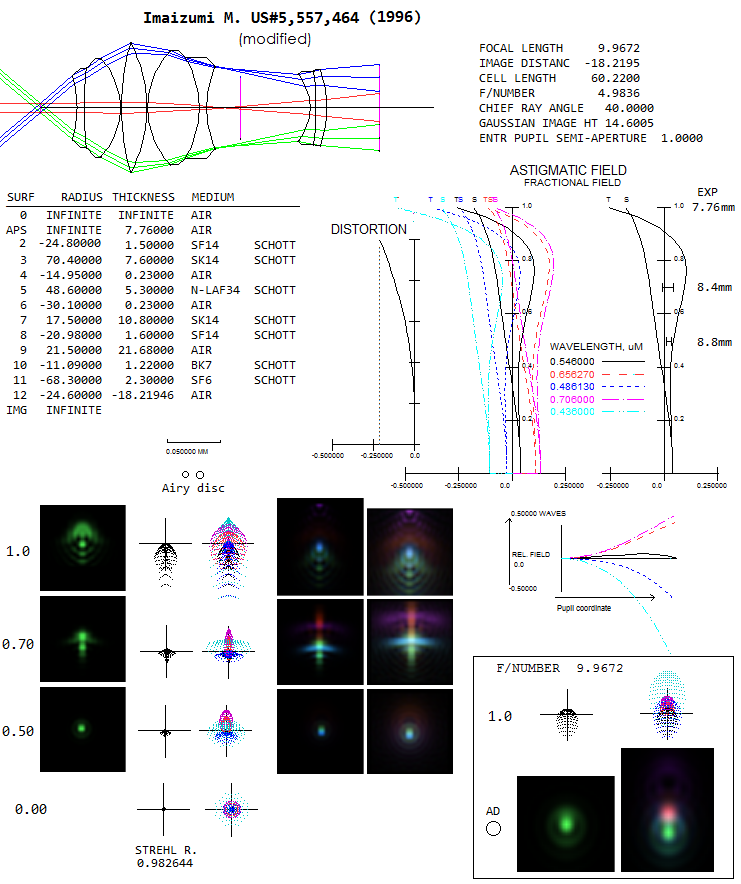
At f/5 its edge performance leaves something to be desired,
as well as its longitudinal chromatic correction, but
remain within acceptable. Overall, it is in the 80° AFOV performance
category (more so considering likely improvement after optimization),
and it was achieved just by adding Smyth lens to a ~65° AFOV configuration
(the Airy disc at f/5 is midway between the two circles shown; scale
is to small to draw it accurately with given screen resolution). Field
is flat to beyond 80% radius, with the vey edge requiring about +2
diopters (infinity to 0.5m) accommodation (since edge point is closer
to the eyepiece, when focused on the mid field it will cause the
exit pencil come out not collimated, but slightly diverging, requiring
natural, positive accommodation). Exit pupil shift is little over 1mm,
much smaller than in the patented Naglers.
Nagler 2 (1988a) in its patented design has significantly reduced eye relief vs. Nagler 1, and
exit pupil shift of ~3.6mm, only slightly less relative to the central field
pupil, but significantly smaller nominally. The field is flat to -0.06mm,
or -0.6 diopters. Axial color correction not quite as good, but still
more than satisfactory, and lateral color correction is similar, except for
the violet end, which is significantly worse. An interesting coparison
with the Smyth lens design from the far 1923. (Taylor, #1,468,762, filed 1920)
shows that Smyth lens alone is not enough. Patented as a binocular eyepiece
coupled with a small 0.85-inch achromat at 10x magnification
(somewhat more, with the eyepiece f.l. of 6.2mm and f/3.5 objective),
it focused on obtaining flat field and corrected astigmatism.
For some reason, that was achieved only near field edge (with some
residual negative coma to the tune of 0.4 wave P-V at f/5), while the inner field
suffered from significant astigmatism - roughly three times
the Airy disc diameter at f/5 - which at f/3.5 leaves something to be
desired even at 10x magnification. Lateral color correction is
not quite acceptable at f/10, but eye relief is comfortable, and
the exit pupil shift negligibly small.
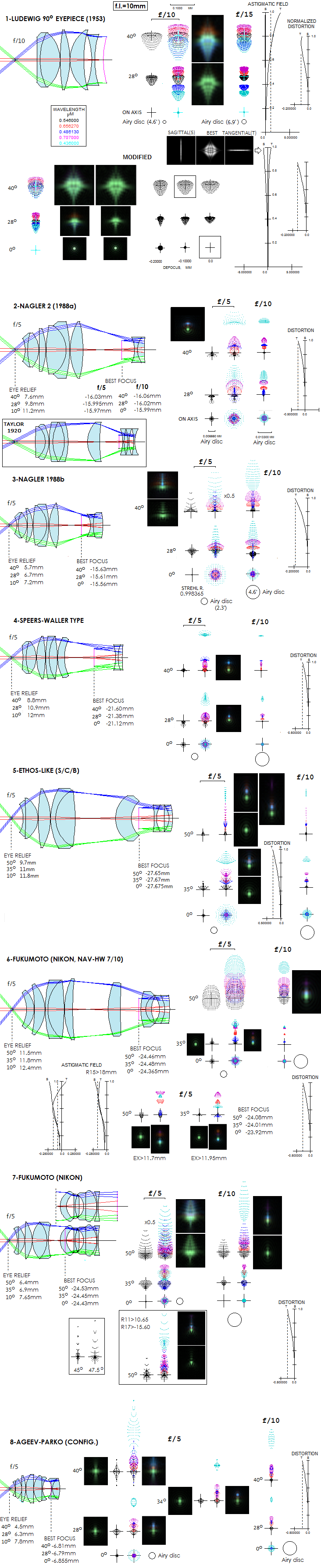
The 1988b Nagler has everything significantly smaller, including
eye relief, which makes it more suitable for the longer f.l. units.
It has somewhat more astigmatism - enough to bloat Airy pattern
into unrecognizable shape - and similar color correction, with
somewhat less of the violet lateral color error. The Speers-Waller
configuration here illustrates the gain from allowing for field curvature.
Astigmatism is low enough to leave Airy pattern preserved over the
entire 40° field radius, but the required field edge accommodation
of -5.8 diopters is more than what most people could handle (for 10mm f.l.;
since the diopter equivalent in mm changes with f2/1000, the 20mm
f.l. unit, with twice larger longitudinal astigmatism, would require
half as strong edge accommodation). This same configuration could be
slightly modified to one with acceptable field curvature, and still
a very good correcction of astigmatism; if, for instance, R15 is made 88mm
and rescaled to 10mm f.l., edge accommodtion drops to -3.7 with the
Airy pattern mainly preserved across the field. This arrangement has a good eye relief, and
somewhat reduced exit pupil shift. Ethos-like design by
Smith/Ceragioli/Berry, shows nothing short of amazing correction, with
one exception: lateral color. It, of course, doesn't imply that the
actual Ethos has it in similar magnitude, but this design would have it
noticeable, as the simulations for the mesopic eye mode suggest. The
exit pupil shift is further reduced. The Fukumoto Nikon patent from 2013.
has excellent field correction, except the last 20% of the radius, or so. Lateral
color error is, again, less than satisfactory. It is interesting
that the edge astigmatism can be nearly eliminated by a correction of
a single radius (R15, from 18.8mm to 18mm, with a small correction in
exit pupil location, to keep the ligh cone in a proper orientation),
with even the lateral color somewhat improved. The only purpose of the
edge astigmatism could be to keep the field flatter, with the edge
accommodation kept below -1 diopter, at -0.8. But twice stronger
accommodation required with the astigmatism greatly reduced is still
quite comfortable for most people (infinity to 0.63m). The smaller
Fukumoto has so much of edge astigmatism that the spot had to be
reduced to half its size. Unlike its larger cousin, it affects only the edge
area; even at 47.5° the spot is significantly smaller, as shown
in the smaller box at left. The edge astigmatism can also be significantly
reduced by a small change in two radii, with the dominant aberration
remaining at 50° being trefoil. Lateral color error is still too large.
Finally, the miniature in comparison Ageev-style design has also the
shortest eye relief (which according to the patent description should be
somewhat longer with the actual unit, 80% of the focal length), has good correction over the
practically flat field, but the lateral color error is again the weakest point.
Note that the patent document (RU2548745C1) gives illustration of the
lens assembly, but describes the glasses only in general terms, without
specified radii/separations. Hence this particular design is not to
reflect the actual unit's performance, rather to show that such configuration
can indeed achieve a high level of correction. The astigmatic plot given in the
patent document is unusual in that tangential and sagittal surfaces
cross twice before beginning to spread wider at the 50° mark.
Maximum accommodation requred, according to the plot, is between -0.05mm
and 0.07mm for 12.5mm f.l. unit which, with one diopter of defocus given by
12.52/1000=0.156mm, translates to -1/3 and nearly +1/2 diopters,
respectively.
As a curiosity, a design that shows how much can do Smyth configuration
consisting of three singlets. It is T. Clarke design from 1983. that comes
in several arrangements, from a single-glass to multi-glass combination.
The author claims they can be used down to f/3 and 40° field
diameter. Raytrace by OSLO does not seem to be confirming that, at
least not for the field claimed. Below are bot reverse (top) and
direct raytrace of the 1-inch focal length arrangement that does use some fancy glasses
(and does significantly better than the BK7/SF2/BK7 combination). Both
are with the same ray geometry, based on 1000mm f.l. f/10 objective
(OSLO "perfect lens" in direct raytracing, with another "perfect lens"
on the eye end). For comparison with 10mm f.l. units above, at 10mm
f.l. the blur size and lateral color would be 2.54 times smaller, and
distortion would remain unchanged.

The outputs at f/10 are similar, but not identical, given for axis,
14° and 20° field radius, for best focus locations (i.e. with
full accommodation). Reverse raytracing gives distortion
of opposite sign to that in direct raytracing, with the sign and magnitude
of it indicated by the mismatch between the marginal (blue) focusing
cone and end point of the Gaussian image (solid line, distortion graphs).
Astigmatic fields are also different, although nearly equilizing in
magnitude toward field edge (main reason is that the fixed exit pupil distance
in reverse raytracing is correct for the field edge cone, but becomes
increasingly inaccurate closer to the field center; for instance, correct
exit pupil separation for 10° field radius is 32mm, which produces
only a bit more astigmatism at that field height than direct raytracing,
with proportionally smaller field curvature).
The 20° ray spot plot for f/5 system, shown at left and up from the
tri-color 20° spot, indicates insufficient edge correction at this
focal ratio already (note that astigmatic field, determining
longitudinal astigmatism, doesn't change
with the focal ratio, but the aberration increases due to the combined
effect of larger transferse aberration - i.e. wider cone - and smaller
Airy disc).
Direct raytracing - which shows the actual eyepiece aberration -
shows that astigmatism is negligible for about 60% of the field radius,
partly supporting claim that the eyepiece could be used down to f/3
focal ratio. Hoever, at the 70% radius longitudinal astigmatism is
already about 0.2mm, which at f/3 translates to 5 waves P-V wavefront
error, i.e. blur of some eight Airy disc diameters. With the angular
diameter of Airy disc in arc minutes given by 4.6F/f, for 25mm f.l. (f)
eyepiece and F=3 it implies 4.3 arc minute blur, appearing as a spot
to most people. But astigmatismm plot doesn't show coma, which increases
inversely to the 3rd power of f-ratio, and becomes dominant at f/3,
with about 1.5 times larger RMS wavefront error.
Knowing that the coma blur is 2.5 times larger than astigmatism blur for
the same magnitude of aberration, implies that the actual blur is
roughly 15 arc minutes, half the diameter of full Moon (in addition,
there's over half a wave of spherical aberration). At f/5, astigmatism
is almost three, and coma almost five times smaller, making the blur
roughly five times smaller, around 3 arc minutes, which can be deemed
passable for the outer 30% of field radius.
Field edge accommodation requirement is little
over 0.5mm, which for f=25.4mm f.l. eyepiece translates to less than 1
diopter (one diopter of accommodation being given by f2/1000).
Direct raytrace shows that this point falls beyond retina, the
consequence of a slightly diverging pencil coming out of the eyepiece.
It requires contraction of eye lens, which is natural accommodation
much easier on the eye than that of opposite sign.
◄
12.3. Eyepiece aberrations II
▐
13. THE EYE
►
Home | Comments
|