• Distortion
• Chromatism
• Spherical aberration of the exit pupil
• Diverging entrance beams (Barlow)
Previous page covers the three main monochromatic aberrations,
affecting point image quality, and best image surface curvature,
affecting image surface. Somewhat less of concern, due to being
either not point image aberrations, or of a relatively low level,
are image distortion, chromatism, spherical aberration of the exit
pupil and aberrations induced by diverging cones entering eyepiece,
common with the standard Barlow lenses.
Eyepiece distortion
Due to
the eyepiece being working with much larger field
angles than the objective, image distortion becomes significant aberration.
As explained in 2.6. Distortion, it is
caused by a change of magnification with the field angle,
shifting Gaussian image point
away from its ideal
position. There is no effect on point-image quality, only its position
in the image space. Distortion has two different forms, linear and angular
(FIG. 212).
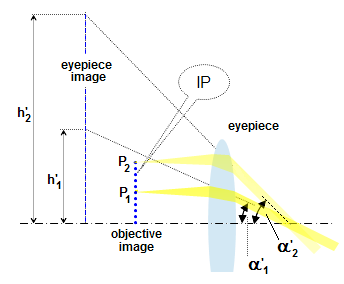 FIGURE
212: Image
distortion in
the eyepiece is a result of large apparent angles it
produces. The difference between relatively large angle (in radians)
and its tangent becomes significant. As a result, if the projected
apparent heights h'1
and h'2 are proportional to the appropriate point-source P1
and P2
heights in the object image plane (IP), then the ocular-produced angles
α'1
and α'2
can't be proportional to the appropriate field angles
α1
and α2
at which the
point-source heights are seen in the object image plane - and the other
way around. When the heights are not proportionally imaged, the
eyepiece suffers from linear (or rectilinear) distortion, which can be negative (barrel
distortion, with the length of a given linear section decreasing with field angle) or positive (pincushion distortion, with the length of a given linear section increasing with field angle). Likewise, when the
angles are not proportionally re-imaged, eyepiece suffers from
angular
distortion - also either positive or negative - which manifests itself
by elongating objects, vertically or horizontally, farther out in the field.
Obviously, the two forms of field distortion can't be both cancelled
at the same time. In amateur astronomy, the preference is, in
general, minimized linear distortion, for esthetic reasons. In
professional astronomy, angular precision is more important.
FIGURE
212: Image
distortion in
the eyepiece is a result of large apparent angles it
produces. The difference between relatively large angle (in radians)
and its tangent becomes significant. As a result, if the projected
apparent heights h'1
and h'2 are proportional to the appropriate point-source P1
and P2
heights in the object image plane (IP), then the ocular-produced angles
α'1
and α'2
can't be proportional to the appropriate field angles
α1
and α2
at which the
point-source heights are seen in the object image plane - and the other
way around. When the heights are not proportionally imaged, the
eyepiece suffers from linear (or rectilinear) distortion, which can be negative (barrel
distortion, with the length of a given linear section decreasing with field angle) or positive (pincushion distortion, with the length of a given linear section increasing with field angle). Likewise, when the
angles are not proportionally re-imaged, eyepiece suffers from
angular
distortion - also either positive or negative - which manifests itself
by elongating objects, vertically or horizontally, farther out in the field.
Obviously, the two forms of field distortion can't be both cancelled
at the same time. In amateur astronomy, the preference is, in
general, minimized linear distortion, for esthetic reasons. In
professional astronomy, angular precision is more important.
Discrepancy between (recti)linear and angular distortion is a consequence of large viewing angles typically associated with eyepieces. Illustration below shows the relation between apparent angles and equal linear sections for small and large (magnified) image, where the magnified image has zero rectilinear distortion, i.e. every linear segment of field radius is equally magnified. In such case, due to large viewing angles, upper radius of a circular shape near field edge (or anywhere in the field where distortion is large enough) will appear smaller than the lower one,
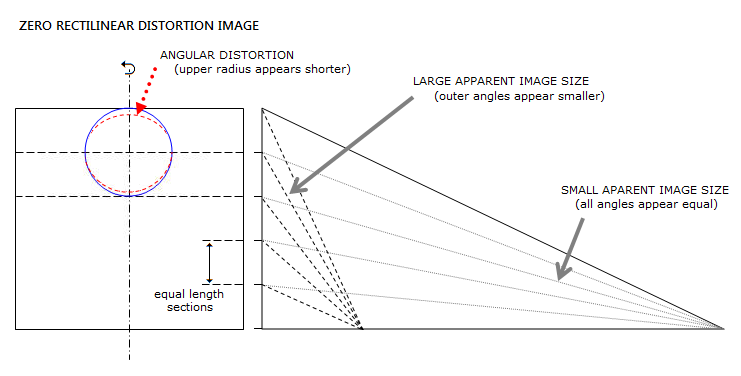
and the circular form - despite being perfectly re-imaged in geometrical
sense - will appear as if having flattened top. In order for it to
appear without such distortion, the top radius has to be longer as
needed to make its apparent viewing angle equal to that of the lower
radius. In other words, it requires a specific amount of (positive)
rectilinear distortion (if it exceeds needed amount, the shape will
appear elongated toward edge). Which, in turn, will produce field
distortion shown on the distortion page.
It is in more detail shown below. The black square diagonal equals the
Gaussian (distortion-free) image diameter, and the red grid shows
deformation of the square due to distortion.

Positive distortion appears more pronounced, both as the deformation,
and on the plot, but the relative magnitude of distortion is nearly identical
for either form: about -0.7 (-30%) negative, and +1.4 (+40%) positive.
Most eyepieces exhibit both forms of
distortion, although one is usually dominant. In astronomy, angular
attributes are more important than linear, although in amateur astronomy
the aesthetic quality of low linear distortion is usually more of a
priority. Manufacturers seldom
give the specs on eyepiece distortion; linear distortion, expressed as a
percent, %ld=100(1-tanα'/tanα),
with α'
being the actual angle, and
α
the ideal (zero distortion) angle, is considered negligible if up to ~5%
for conventional ~40-degree apparent field of view (AFOV) eyepieces.
However, since it increases with the third power of field angle, it is
hard to control with wide AFOVs. Consequently,
wide-field eyepieces can
have it exceeding 20%.
Likewise, the percent of angular distortion can be expressed as
%a.d.=100(1-α'/α).
Eyepiece chromatism
In well designed and made eyepieces, chromatism can be expected to be cancelled longitudinally.
Lateral chromatism is more hard to correct, the wider eyepiece field, the more so.
Even ordinary oculars can have noticeable amounts of it as well.
This is particularly the case with the old eyepiece types, from the simplest
ones, like the Huygenian and Ramsden, to the more complex older widefields.
Due to more sophisticated designing and better glass choices, the more complex
types now usually can be made with good to excellent chromatic correction.
Eyepieces raytraced below should illustrate the level of correction in
present time quality eyepieces.
(FIG.
213).
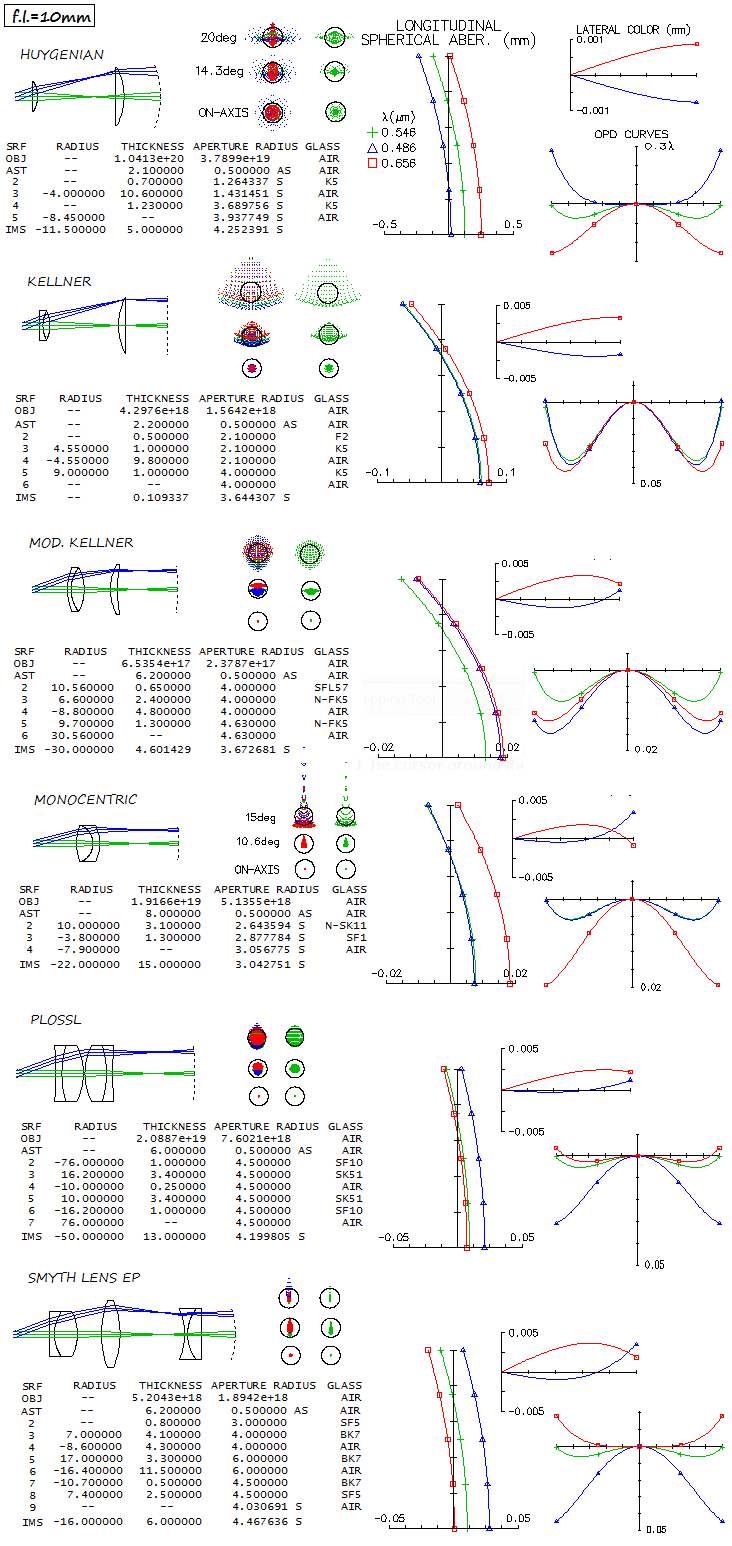 FIGURE 213: Some conventional eyepiece types in the amateur
astronomy, with ray spot diagrams illustrating their typical
aberrations in e (green), F (blue) and C (red) spectral lines. The
spots are given for f/10 focal ratio, for the field center, 14.3° and
20° off-axis (black circles are the e-line Airy disc).
Since this is reverse raytracing, the numerical thickness under the 1st surface
(aperture stop, AST) represents eye relief.
Axial color
correction is good for all. Lateral color - which increases with
the field angle - is good to acceptable, in
general, although may not be at the fast focal ratios, when it is more pronounced
due to the smaller Airy disc.
Longitudinal and lateral chromatism don't change with the
focal ratio nominally, but since the Airy disc size changes in inverse proportion to it,
axial chromatism in effect changes in proportion to the square of focal ratio
(since transverse aberration changes opposite to the Airy disc), and lateral
color only in proportion to it. This means that the former is
four times greater at f/5 than at f/10, and the latter only twice.
Since spherical aberration changes with
the 4th power of focal ratio, and astigmatism with the square of it,
increase in chromatism at the faster focal ratios can be overshadowed
by these two, particularly the former which, changing the nature of the
error, can even diminish chromatism (for any given longitudinal defocus,
the P-V wavefront error is eight times smaller for spherical aberration
than defocus).
FIGURE 213: Some conventional eyepiece types in the amateur
astronomy, with ray spot diagrams illustrating their typical
aberrations in e (green), F (blue) and C (red) spectral lines. The
spots are given for f/10 focal ratio, for the field center, 14.3° and
20° off-axis (black circles are the e-line Airy disc).
Since this is reverse raytracing, the numerical thickness under the 1st surface
(aperture stop, AST) represents eye relief.
Axial color
correction is good for all. Lateral color - which increases with
the field angle - is good to acceptable, in
general, although may not be at the fast focal ratios, when it is more pronounced
due to the smaller Airy disc.
Longitudinal and lateral chromatism don't change with the
focal ratio nominally, but since the Airy disc size changes in inverse proportion to it,
axial chromatism in effect changes in proportion to the square of focal ratio
(since transverse aberration changes opposite to the Airy disc), and lateral
color only in proportion to it. This means that the former is
four times greater at f/5 than at f/10, and the latter only twice.
Since spherical aberration changes with
the 4th power of focal ratio, and astigmatism with the square of it,
increase in chromatism at the faster focal ratios can be overshadowed
by these two, particularly the former which, changing the nature of the
error, can even diminish chromatism (for any given longitudinal defocus,
the P-V wavefront error is eight times smaller for spherical aberration
than defocus).
The Huygenian (from "Telescopes, eyepieces, astrographs" by Smith, Ceragioli
and Berry, except that the lenses are thinner, for 0.4mm longer eye relief)
has probably as good overall correction - including color correction - as
possible with this simple design. Best focus spherical aberration ray spot plot
already nearly fills the Airy disc, which means that at f/5 would be some
16 Airy discs large, or about 1 wave P-V. The Kellner (also called achromatized Ramsden)
from the same book, is probably deliberately given in configuration close to its simpler
predecessor (Ramsden), in that its field lens nearly coincides with the objective's
image, and the exit pupil with the rear lens - the condition for minimizing
lateral color in the Ramsden. The eye relief is more likely to be about 1.8mm
with most telescopes (2.2mm eye relief would be with a 10-inch f.l. objective), and in
that case astigmatism is somewhat reduced, and best field goes from nearly flat
to acceptably curved. This design has practically zero longitudinal chromatism,
and spherical aberration is lower than in the Huygenian. Lateral color correction,
however, leaves something to be desired. It could be easily corrected by increasing
lens separation to nearly 11mm and weakening somewhat the field lens, in order to
preserve flat field. Eye relief also increases to 4mm, however, the objective's image is still nearly touching
the field lens - only on its inner side - which is undesirable. In order to come
to a better overall design, more radical changes are necessary. One such Kellner
modification is shown, with significantly smaller lens separation, and longer eye relief.
Astigmatism is further reduced (with some acceptable field curvature),
and longitudinal chromatism is even lower. The following design, comparable in
correction to the monocentric eyepiece given in the aformentioned book,
shows that this kind of correction can be achieved with only two cemented
lenses (note that the name monocentric - implying concentric surfaces -
is not appropriate for neither; they are simply cemented doublet and triplet
respectively). A well designed Plossl is the standard measure of eyepiece correction,
and the one in Albert Nagler's patent documentation is such a design. In fact,
if its field would expand to 65° it would have better field correction
than most 5-element Erfles). Finally, a very basic Smyth lens design illustrates high correction
levels of this eyepiece type over the conventional eyepiece field.
For up to three times wider fields more elements and fancier glasses
are a must. Commonly, compromises have to be made, that may include
compromises in (less than perfect) chromatic correction as a trade off
for a flatter, low-astigmatism field.
It should be noted that significant
variations in the amount of any specific aberration is possible within the
same eyepiece type, depending on the design goal and design/fabrication
quality.
Eyepieces often have longitudinal chromatism
as some form of primary chromatism: shorter and longer wavelengths focus on the opposite
sides of the mid (green-yellow) wavelengths. Above designs give good idea about the magnitude of eyepiece longitudinal chromatism,
and how negligible is its chromatic effect. For comparison, longitudinal spectrum
in the same wavelength range stretches over nearly 2.5mm in a 100mm f/12
achromat, considered generally acceptable in that respect. The effect of the
eyepiece can be directly judged based on their respective LA graphs. Since
the eyepiece LA graph is a product of reverse raytracing, with collimated light entering
through exit pupil and exiting through field lens, it means that the aberration
in the objective focal plane will produce perfect collimated pencils exiting eyepiece
if it is of the exact shape, magnitude, and orientation as the aberration produced by
reverse raytracing. This means that if we look at the LA graphs of the Plossl above,
and a 100mm f/12 achromat below, eyepiece chromatism will reduce the achromat's
g-line (436nm) error by less than 0.05mm, F-line (486nm) error by 0.02mm, and C (656nm)
and r-line (707nm) by less than 0.01mm.
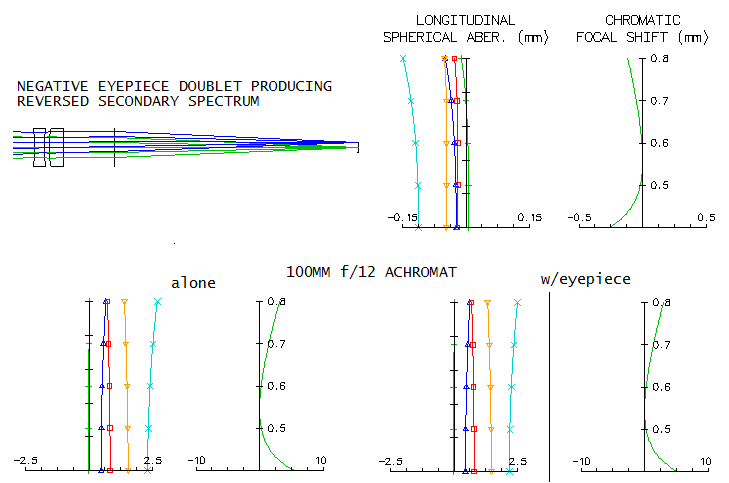
Even if we'd try to design eyepiece so that its form of longitudinal
chromatism is the same, with the opposite sign to that of the achromat,
it would be very hard to generate that much of aberration on such a small
scale. The simplest form of it would have been a negative reversed doublet
(BK7 for the negative lens and F2 for the positive) placed
at its focal length in front of the objective's focal plane (vertical line
crossing the rays behind the eyepiece is the "perfect lens", focusing collimated
beams exiting the eyepiece, playing the role of a perfect eye). Top shows
the "eyepiece" and longitudinal chromatism it produces (C and F lines are
coinciding with their paraxial foci, so that it doesn't change their mutual
position in the achromat). Even the
-53mm f.l. eyepiece of this kind shown - and the error generated scales
with focal length - would change very little in the achromats longitudinal
error (the biggest gain would be reduction in the violet line from 4.94 to
4.7 waves P-V). To accumulate the error of needed magnitude, such eyepiece -
or rather corrector - would need to employ multiple elements with special
glasses, and it may not be practical, or marketable. A challenge of its own
is controlling astigmatism/field curvature
of such a lens close to the focal plane.
Spherical aberration of the exit pupil
The
last eyepiece aberration to address is spherical aberration of the exit
pupil. Ideally, telescope ocular will re-image the aperture into a
single plane; in other words, all the bundles of parallel rays exiting
the ocular would merge into a common circle symmetrical around the optical axis
(FIG. 209). In reality, in re-imaging
the entrance pupil (aperture opening), an eyepiece acts as any positive
lens does - in other words, it suffers from under-correction. As a
result, object-image points toward the edge will cross closer to the eye lens (FIG.
214). In effect, exit pupils
for the outer zones are shifted toward the eye lens, away from the eye, and -
depending on the extent of shift - it may result in the outer field
either being not visible from the same eye location as the mid-field (central field
area is always visible), or it being vignetted. If the eye needs to be moved back and forth in
order to view the entire field, it may become decentered , having parts of the field vignetted
or lost from the

FIGURE 214: Exaggerated
illustration of the spherical aberration of exit pupil. The eyepiece
(EP) transforms diverging light cones emerging from the image points
into parallel pencils. Those coming from the points
higher in the image plane are intersecting the axis closer to the
eye lens than those from the lower image points. As a result, exit pupils for the
former are shifted closer to the eyepiece.
Large enough pupil separation will make it difficult or
impossible to hold the entire field in view for any single eye
position. The effect can be noticeable in wide-field and long-focus eyepieces, both
having, in general, greater longitudinal exit pupil aberration.
Point image quality is unaffected, only the axial position of its
exiting pencil.

view (the "kidney bean effect"). Other than that,
spherical aberration of the exit pupil doesn't affect image quality (it
only occurs when the light within the pencil exiting the eyepiece is not collimated). Also, it
can be minimized in any particular design, and not all wide-field or
long-focus eyepieces necessarily suffer from it to a significant degree.
Below is an actual raytrace of a simple wide-field eyepiece with
a significant exit pupil shift. The shift increases exponentially
toward field edge, with the last 1/3 of the field radius accounting for
over 70% of the entire shift.
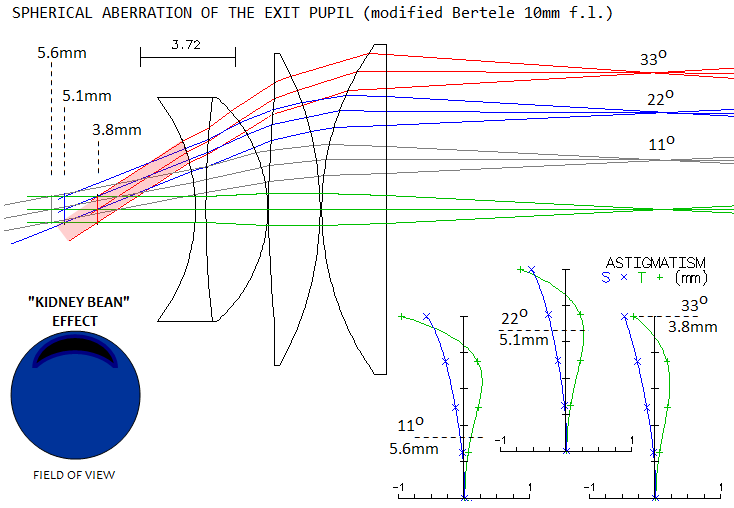
If eye pupil is pulled back and/or up from the edge area exit pupil (contained
in the redish pencil) light from that area won't enter the eye,
or will enter it only partially, especially when eye pupil is not
significantly larger than the exit pupil. It will cause ghostly
darkening of that part of the field ("kidney bean effect"). The
astigmatic fields bottom right illustrate how the raytraced field changes
with any fixed exit pupil location; in general, the farther field
area from the one for which the exit pupil is appropriate, the
greater distortion of the actual field (from left to right: field
raytraced from 11°, 22° and 33° exit pupil, respectively).
The central field remains relatively unaffected, since those ray
pencils use midely curved lens portions, and change in the pencil
height is relatively small. As can be grasped from the image,
kidney bean effect is more likely to be noticeable at larger
exit pupil sizes.
There is a number of eyepiece designs, but
vast majority of those used in astronomy are variations of just a few
basic configurations (FIG. 215). In general, more elements allow better
overall correction, but at the price of increased scatter and absorption
of light. The exit pupil range in the figure below indicates the extent
of the spherical aberration of exit pupil for the few basic eyepiece
types.
 FIGURE
215:
Basic forms of astronomical eyepiece, with its front focal point coinciding with the focal plane FP
of the objective.
Ex indicates the extent of spherical aberration of the
exit pupil, normally not troublesome in conventional eyepiece types. The simplest
of them - Kellner
- features 45-50 deg. apparent field and satisfactory correction for
spherical aberration at ~f/5 and slower f-ratios. Plossl has better
overall correction, setting quality standards for conventional
eyepieces. Orthoscopic
(Abbe)
usually has somewhat smaller field than Plossl, not due to
inherently inferior field definition, but for its high standards
and customary use for planetary observing.
Conventional wide-fields, Konig
and Erfle, have better spherical
correction than Kellner, but more intrusive edge astigmatism, due to
their larger, 60-70 deg. fields. Most of today's standard wide-fields
are variations of these two basic concepts.
Nagler
(Type 1),
whose negative front lens allows for better correction of astigmatism,
offers well corrected fields exceeding 80°. Its wide exit pupil
range indicates more intrusive spherical aberration of the exit
pupil ("kidney bean effect"), better corrected with later types.
Darker color indicates glass of higher refractive indici.
(data from Telescope Optics, Rutten/Venrooij).
FIGURE
215:
Basic forms of astronomical eyepiece, with its front focal point coinciding with the focal plane FP
of the objective.
Ex indicates the extent of spherical aberration of the
exit pupil, normally not troublesome in conventional eyepiece types. The simplest
of them - Kellner
- features 45-50 deg. apparent field and satisfactory correction for
spherical aberration at ~f/5 and slower f-ratios. Plossl has better
overall correction, setting quality standards for conventional
eyepieces. Orthoscopic
(Abbe)
usually has somewhat smaller field than Plossl, not due to
inherently inferior field definition, but for its high standards
and customary use for planetary observing.
Conventional wide-fields, Konig
and Erfle, have better spherical
correction than Kellner, but more intrusive edge astigmatism, due to
their larger, 60-70 deg. fields. Most of today's standard wide-fields
are variations of these two basic concepts.
Nagler
(Type 1),
whose negative front lens allows for better correction of astigmatism,
offers well corrected fields exceeding 80°. Its wide exit pupil
range indicates more intrusive spherical aberration of the exit
pupil ("kidney bean effect"), better corrected with later types.
Darker color indicates glass of higher refractive indici.
(data from Telescope Optics, Rutten/Venrooij).
Diverging entrance beams (Barlow)
Over time, the standard Barlow lens was becoming shorter, which
at any given Barlow magnification factor means that it was
producing more strongly diverging exit beams. On the other hand,
telescope eyepiece is optimized for a nearly zero divergence,
which is from the standpoint of aberrations induced practically
identical to the very mildly diverging beams coming from the
typical telescope objective (very short focal length objectives, such
as binocular objectives, or very fast mirrors, produce
more widely diverging beams which may cause some added aberrations).
Images below show the effect of entering beams divergence on
eyepiece aberrations. The objective is OSLO "perfect lens", and
so is the eye on the other end, hence all aberrations come only
from the eyepiece - the 10mm Plossl as given in Albert Nagler's
patent application. Shown are a native f/10 system and then
native f/5 system, each with a 2x Barlow lens of approximately
standard length, and with a tzv. "shorty" Barlow.
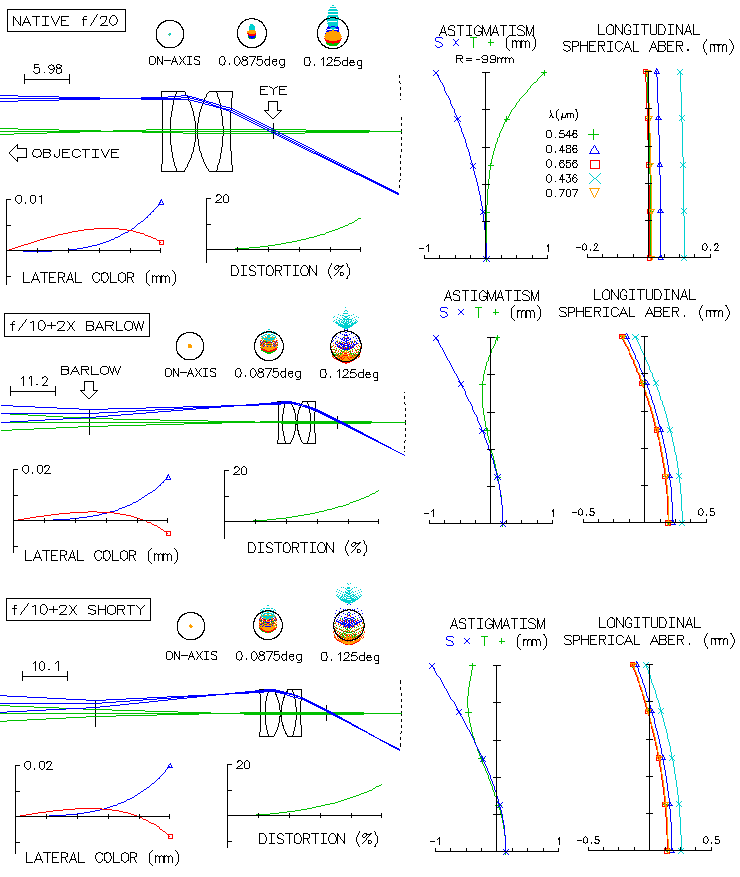
Starting with the native f/20 objective, we see that the aberrations
induced due to the Barlow lens beam divergence are coma, field curvature
and lateral color, generally low in magnitude due to the very narrow
f/20 beam (spherical aberration is not due to beam divergence, but
due to the slightly wider beam entering eyepiece). The exception is
field curvature, with the
required edge accommodation increasing by about 4 diopters with the
standard, and close to 7 diopters with the "shorty" Barlow (for 10mm
f.l. unit; for 20mm unit half as much). Field curvature increase is
due to reduced astigmatism which, being of opposite sign to the
Petzval curvature, reduces best image curvature. Also, the eye
relief - the eyepiece to exit pupil separation - increases with the
beam divergence, being about 20% larger with the "shorty" Barlow,
than in the native f/20 system. Induced aberrations are somewhat
larger with the "shorty" Barlow, but the difference is nearly negligible.
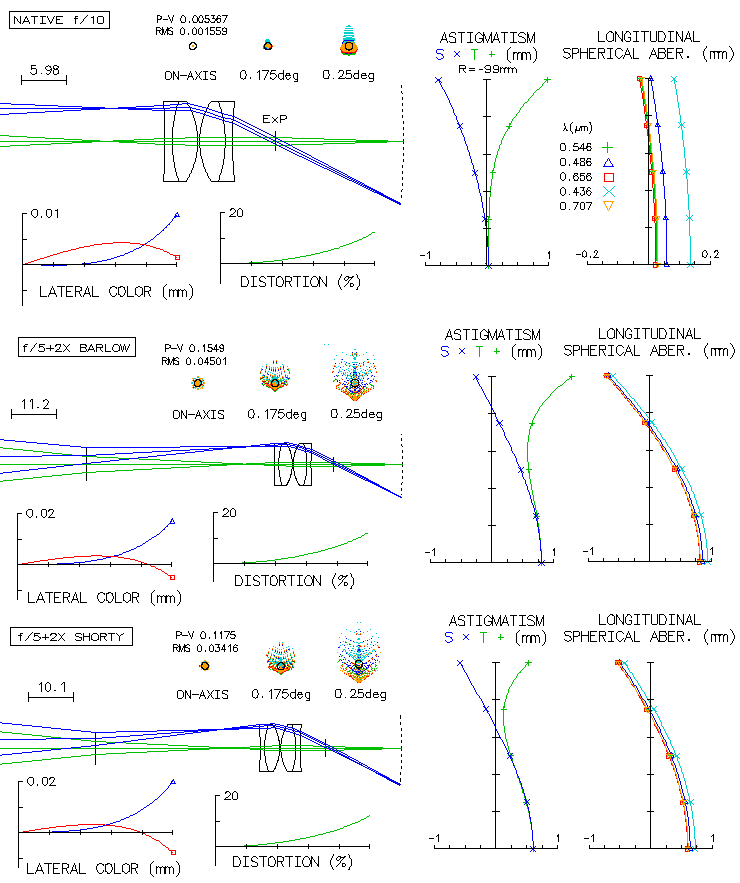
Using the same perfect Barlows on an f/5 perfect system induces
significantly more of coma, with the other divergence-related
aberrations being of similar magnitude (the astigmatism plots have
origin in the paraxial focus, and in order for the axial and
field edge point image to belong to the same spherical surface
the latter - for pure primary astigmatism midway between sagittal
and tangential focus - has to lay on approximately the vertical line drawn
from the origin;
hence the differential with respect to the vertical drawn from the origin
determines the required accommodation; the origin represents best
focus point, which is in the presence of spherical aberration
shifted away from paraxial focus). The aberrations induced
vary with the eyepiece type, possibly significantly, but those that
are likely to be significant are field curvature and coma, the latter
when using Barlow lens with faster systems. Field curvature is a
consequence of the change in eyepiece astigmatism, and could be both,
positive and negative. And whether it is one or the other depends
on the sign and magnitude of the image field curvature of the objective.
◄
12.2. Eyepiece aberrations I
▐
12.4. Telescope eyepiece: comparative
raytracing
►
Home
| Comments