|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
6.2.General effects of aberrations
▐
6.3.2. Aberrations and extended
objects ► 6.3. Effect of telescope aberrations on optical image; point-image
PAGE HIGHLIGHTS For any given nominal aberration, the effect on image quality perceived by the eye will depend on several factors. The most important are:
(1) object/detail size, It will be helpful to clarify some basic terminology. While the effect of diffraction is often treated as something different than the effect of aberrations, it is in fact one same phenomenon. What is usually called "diffraction" is the diffraction in aberration-free aperture. However, aberrated apertures merely modify this pattern - and so do obstructed apertures - into another one with different properties. In general, we can say that optical aberrations worsen diffraction effect, and that it is at its minimum in an aberration-free (still not "perfect") aperture. In other words, aberrated diffraction patterns are diffraction patterns resulting from non-spherical wavefronts.
Effect of any given magnitude of aberration changes in inverse proportion
to object size
.
It is because any given diffraction pattern becomes
effectively smaller as object size increases, which is no different
from the pattern - i.e. aberration - becoming smaller with given
object size (this effect is familiar from the MTF graph, where any
level of aberration has less effect on contrast transfer as the
frequency nears zero, i.e. an infinitely wide line pair, where
image contrast reaches that of the object). Image below
shows effect of aberration-free diffraction pattern, where
size of object - in this case square wave patterns, generated
by SYNOPSYS - diminishes
or, alternately, diffraction pattern becomes larger from top to
bottom, doubling at each next image (left).
The top pattern can be regarded as the object, with no appreciable
diffraction effect. Adding any aberration at a level where the
effect of diffraction alone is not negligible (shown
diffraction pattern and the square wave are on the same scale)
causes transfer of energy away from the
center of diffraction pattern which, in general, further worsens
image contrast. This is noticeable in the pattern
image even if the added aberratios are at the "diffraction limited"
level (right). Since the line separation is about eight Airy disc
diameters, or 20λF wide, it corresponds to ~0.05 normalized
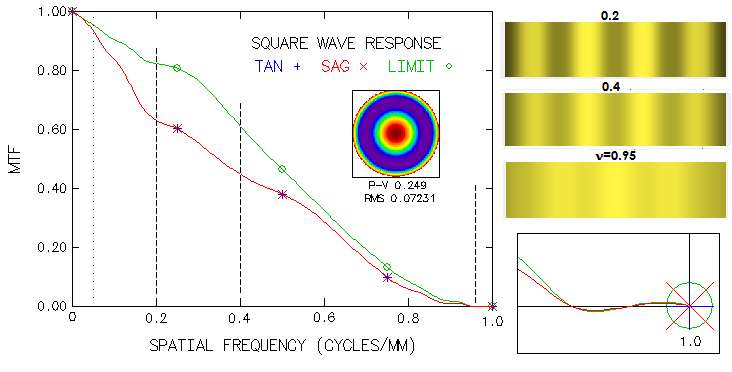
frequency. Plot below shows contrast transfer for unaberrated aperture and
aberrated with nearly 1/4 wave P-V of primary spherical aberration.
At 0.05 frequency nominal contrast drop is still small; at 0.2
frequency the line pair is about two Airy disc diameters wide,
half as much at 0.4, and about λF at the cutoff. Near the
cutoff there is contrast reversal, when transfer becomes negative
(magnified in the box at right).
It will take roughly twice larger object - i.e. twice wider line pair - to
equilize contrast of 1/4 wave P-V aberrated images vs. unaberrated. Even at
this, still low aberration level, differences in effect of these
aberrations are noticeable, with spherical aberration spreading
energy more than the others; this affects images of relatively large
objects - approximately one to four Airy disc diameters -
more than with other aberrations, but less with images of small
object, closer to the limit of resolution (it should be noticeable
if aberrations are added to the bottom pattern in the first image).
How much optical aberrations affect image quality is directly dependant
on image
magnification. Large aberrations may
be entirely invisible at low magnifications and, vice versa, quite small
aberrations may noticeably impair image quality at high magnifications.
In order to establish some general guidelines in respect to the effect
of aberrations, it is necessary to start with the visibility of
diffraction effects in a perfect aperture. The two
main object types to consider are: (1) point-like (stellar), and (2) extended.
Along with their angular size on the retina, important properties of
either type are their brightness and inherent contrast, both having
great
effect on image appearance in either perfect or aberrated aperture
(since the diffraction minimum itself acts as an aberration even in a
perfect aperture). In general, the brighter image, the more of
imperfections (aberrations) it will show, while higher inherent contrast
makes the effect of aberrations less detrimental.
However, the very basic consideration starts with the
determinants set by the eye itself. For the effect of
diffraction to be noticed, retinal image has to be large enough for the
brain to create an image of finite dimensions. This requires retinal
image extending over at least three cone cells (FIG.
18). With the angular size of
the smallest cones (in the middle of the retina) being ~1/2 arc minute, it is
approximately 1.5 arc minutes in diameter. Angular size of the retinal
image needed for the average eye to start recognizing its
shape is about twice as large, or ~3 arc minutes for bright, contrasty
details. For low-contrast details, it is roughly double, or ~6 arc
minutes, on average. Anything smaller than
~1 arc minute appears point-like to the eye, hence neither diffraction
minimum, nor whatever amount of aberration in might be containing in
addition, is not visible. The larger retinal image, the more apparent
will be the effect of aberration on image quality. Angular size of a
point-like object, such as star, in a
perfect aperture depends on its brightness on the retina. It is determined by
star's apparent brightness and, given light transmission coefficient, aperture
size. In brightest stars, the first bright diffraction ring will appear
nearly as bright as central disc of the diffraction pattern, with the
disc itself being nearly as large as the Airy disc. Since the diameter of
the first bright ring is about 1.8 times the Airy disc diameter, or
about 8/D in arc minutes for telescope aperture D in mm (1/3D for
D in inches), diffraction pattern of a bright star starts appearing
non-stellar at a relative magnification M~0.2D for D in mm, or
M~5D for D in inches (which is the same as 5x per inch of
aperture). The form starts emerging with magnification about doubled, at
~0.4D for D in mm, and ~10D for D in inches. Its form becomes
clearly defined with magnification increased by another factor of ~2. Stars of average
brightness, somewhere between the brightest and faintest visible will
have significantly smaller visible central disc - approximately half the
Airy disc diameter - with no noticeable ring structure. Since
the ring, due to its faintness, is not visible before the disc itself
becomes non-stellar, respective magnifications needed to visually
recognize such a star as non-point-like object are
nearly four times higher than for a bright star. And stars close to the
limit of detection will remain tiny patches of light within the range of
usable magnification. This is how the eye
perceives diffraction minimum (i.e. diffraction in
aberration-free aperture) for point-like objects. Hence, we may conclude
that point-object images in an aberration-free aperture do not
appreciably differ from perfect as long as magnification remains below
0.2D for the aperture
D in mm, or 5D for D in inches. This limit magnification
grows exponentially with the apparent (telescopic) star brightness. Introduction of
wavefront aberrations in the optical
system causes
transfer of energy from the disc to the ring area. In order to affect appearance of point-object image as seen in
aberration-free aperture, this transfer of energy needs to be
sufficiently significant in its extent and intensity to produce an enlarged
bright portion of the diffraction pattern. Very approximately, this
begins to take place at the aberration level of ~0.15 wave RMS, and
grows roughly in proportion to the error. While the central diffraction
disc does not appreciably change in size at ~0.15 wave RMS error level, the
surrounding energy pattern becomes brighter and generally somewhat larger. This,
in effect, makes image of a point-object that was near-perfect in
aberration-free aperture, now appear slightly more blurry; in other words,
magnification that will not show effects of aberration is lower than
those for aberration-free aperture. However, this will affect mostly
brighter stars; those of lower brightness will not change appreciably,
because the energy expanded out of the central disc is still too faint
to have appreciable visual effect. This makes larger
apertures in general more sensitive to the effect of wavefront errors on
star images, due to their higher visual telescopic brightness. Since the level of
aberrations inherent to amateur telescopes is generally well below 0.15 wave
RMS, the effect of aberrations on visual quality of star images vs. that
in aberration-free aperture may be noticeable, but not significant.
However, there are exceptions to this. One is the size of aberrations
farther off-axis, which is often significantly higher than 0.15 wave
RMS. Another is wavefront error caused by seeing, which can be higher
even in medium-size apertures.
Off-axis aberrations
are usually coma and astigmatism, with the latter being especially large
in conventional eyepieces. Coma is present in all
Newtonian reflectors, with the angular size of sagittal coma in the
eyepiece,
As a consequence of the
magnification factor, i.e. non-point images appearing point-like if
magnified to less than ~3 arc minute, visual coma-free field in the eyepiece is larger
than "diffraction-limited" field in the image formed by the objective.
Substituting h=tanεfe
in Eq.17, sagittal coma in terms
of eyepiece apparent field and focal length is CS=tanεfe/16F2
in mm, and with the P-V wavefront error smaller
than sagittal coma by a factor of 3F, i.e. W=CS/3F=tanεfe/48F3, the P-V wavefront error at the
boundary of visually coma-free field in a 20mm eyepiece in an
f/5
Newtonian is about 2 wave P-V for 550nm wavelength. It is larger than
the "diffraction-limited" coma field (0.42 wave P-V) by a factor of
5,
which means that the linear coma free field here is also as much larger than
the formal
"diffraction-limited" field. This, of course, is very much dependant on the
telescopic star brightness: fainter star will not show deformation
farther off, while on the bright ones will be apparent somewhat closer
to field center. With 5mm eyepiece and
identical AFOV, coma wavefront error at the edge of coma-free field is
four times smaller than in a 20mm eyepiece, or ~1/2 wave P-V, just above
the
"diffraction-limited" 0.42 wave. Sagittal coma is still ~3 arc minutes, but now,
due to higher eyepiece magnification, it is appreciably smaller than the Airy disc
diameter (given by 4.6F/fe,
in arc minutes, for 550nm wavelength). The eyepiece
focal length at which the two are about identical is found from tanεfe/48F3=0.00023
(i.e. for coma at the field radius ε
being at "diffraction-limited" level), giving
fe~F3/90.6tanε.
For an f/5 mirror, it comes to fe~4mm,
and for shorter focal length eyepieces the "coma-free" field defined by
the angular size of sagittal coma below 3 arc minutes becomes smaller
than diffraction-limited field. However, the actual coma-free field, as
seen in the eyepiece, is always larger, since it requires sagittal coma
appreciably larger than the Airy disc to produce noticeable deformation
of the central maxima. Approximately, it takes place with sagittal coma
larger than the Airy disc by a factor of 1.5, which corresponds to about
1.2 wave P-V coma wavefront error.
Again, these criteria
are valid for the stars not too bright nor too faint. Changes in diffraction pattern due to coma
error are less noticeable as telescopic star brightness
subsides, and the visual "coma-free" field becomes, in effect,
larger.
Also, this consideration only includes
mirror coma, while for the actual field quality in the Newtonian, eyepiece astigmatism is significant or dominant factor. Finally, the visual coma-free
field, in the sense of no star deformation visible still has large
enough coma in its outer portion to significantly lower its performance
level with respect to extended objects like Moon, planets and deep sky.
It is similar, in
general, with
off-axis astigmatism, only the numbers are somewhat different. As
mentioned, it is eyepiece astigmatism that usually dominates
off axis in visual observing. A typical conventional eyepiece will have roughly
between feε2/60F2
and feε2/30F2
P-V waves of Seidel astigmatism, ε
being the eyepiece field angle in degrees. A 20mm eyepiece at
f/5 will,
therefore, have about 1.6 wave P-V of astigmatism at the approximate 10°
boundary of the coma-free visual field radius. This already exceeds
coma, which is only ~1 wave P-V this far off. Considering that the
smallest geometric astigmatic blur is about 15% larger than geometric
sagittal coma for given P-V wavefront error (both, geometric and
diffraction, for P-V errors larger than ~, and that the two are roughly
proportional to the the actual diffraction blur for errors greater than
~1/2 wave, the coma-free field boundary would have visible blur nearly
doubled due to the eyepiece astigmatism. In other words, the actual
aberration-free visual field would be somewhat smaller. Also, since
the astigmatism
RMS wavefront error for given P-V error is nearly 14% larger than that
for coma, the combined loss of energy is likely beginning to noticeably
degrade contrast of extended objects before the aberration shows visible
deformation of the diffraction pattern of brighter stars. This means
that the actual aberration-free field, as determined by these two
aberrations alone, is yet smaller. Point source resolution The view that aberrations
quickly impair resolving power of a telescope is not uncommon among the
amateurs , but it is only partially true.
Resolution of low contrast details is, indeed, can be very sensitive even to small
aberrations, but high-contrast details - including near equal in
brightness double stars - may not be. Even aberrations as large that would
entirely wash out low contrast detail resolution, will not necessarily
reduce the resolution of high-contrast detail. The two main deciding
factors are type of aberration and relative orientation of the detail. In the context of point
source resolution, of primary interest is double star resolution.
Simulations at
What simulations suggest is that spherical aberration has little effect on this type of resolution at its "diffraction-limited" level (0.25λ), and even with the error doubled. With a bright star, the brightness of the first bright ring can impair resolution in field conditions (due to seeing error and other induced errors), but the stars are still clearly resolved. Not so with the coma. While an average star will remain clearly resolved at the "diffraction-limited" level (0.42λ), the bright star resolution is impaired, generally more than with 0.5λ of spherical aberration. At double the error, stars are not resolved if their common axis nearly coincides with the axis of aberration - especially bright pairs - while might be only partly resolvable for other orientations (shown 45° and 90° orientations relative to the common axis). Similarly, the "diffraction-limited" level of astigmatism (0.37λ) will little affect resolution of a pair of average brightness if its common axis nearly coincides with the axis of astigmatic spike. If the spike is at 45 degrees, however, resolution will be impaired even at this aberration level for a pair of average brightness, and will vanish with bright stars. At double the astigmatism, a partial resolution with the common axis coinciding with the spike might be possible due to the pattern elongation, but with the spike at 45° a pair of stars at the Rayleigh limit is unresolvable regardless of the pair brightness. As for the effect of 0.3D obstruction, it doesn't seem that it significantly influences resolution of equal doubles. In some instances, it appears that its 10% smaller central maxima does produce a slightly better resolved pair, but that is probably offset by the larger, more intense first bright ring, which not only lowers the contrast against the immediate surroundings, but also would throw more energy over the double in the presence of random movements of the portions of the pattern due to seeing. In general, aberrations
affect much more quickly the resolution of unequal doubles. Simulations
at left show a
At the "diffraction-limited" level of spherical aberration the faint companion is barely detectable in the top of the first bright ring. It completely disappears with the aberration doubled. Coma is shown only at its "diffraction-limited" level, because the faint companion is already undetectable, even with the most favorable orientation when the comatic rings spread to the opposite side from where it is located. This is caused by the pattern of the faint companion being just as much spread by coma, with its central maxima merging with the extended maxima of the bright companion. With astigmatism at its "diffraction-limited" level, the faint companion completely disappears in the spike, if the two coincide. When the spikes is at 45°, a slight brightening between the spikes is detectable, which would quickly disappear with further error increase and the associated pattern enlargement. The obstruction here has only a slight negative effect due to the larger and brighter first bright ring; the smaller central maxima is also likely to be slightly detrimental to resolution of unequal doubles in most situations. Obviously, near equally bright stars of at least average telescopic brightness and those with a faint companion are two different contexts: high vs. low contrast detail. The aberration tolerance is much tighter for the latter which, in general, applies to the extended details as well. In principle, aberrations affect extended detail images through the same basic mechanism, by expanding the image of a point source, but the consequences, as well as detail types, are somewhat different. More on next page. ◄ 6.2.General effects of aberrations ▐ 6.3.2. Aberrations and extended objects ►
|
from 
left
(generated with Aberrator, Cor Berrevoets) illustrate the effect
of three classical aberrations - spherical, coma and astigmatism - on
the resolution of a pair of equal-brightness star separated at the
Rayleigh limit. Each aberration is given at its diffraction limited
level (0.80 Strehl, double column at left), as well as twice larger. For
each aberration and aberration level shown are an average star without
clearly pronounced diffraction rings (left), and a bright star. Finally,
it is all given for unobstructed and 0.3D obstructed aperture.
pair
of stars at the Rayleigh limit separation, with the primary star four
magnitudes brighter. As in previous example, shown are an average, and a
bright star for aberration free aperture, clear as well as 0.3D (30%
linearly) obstructed. However, since the fainter companion is already
invisible with the former (the first bright ring in aberration-free
aperture is nearly as bright as a four magnitudes fainter star), the
remaining simulations only show a bright star.