10.2.3.2. Maksutov-Newtonian telescope

Telescopes with meniscus-type full aperture corrector - usually referred to as Maksutov corrector - are respected among amateurs almost as no other telescope type. Many are inclined to believe that the meniscus gives them some extra optical quality, not achievable with other telescope types. Or, at least, that this kind of telescopes, generally featuring spherical surfaces, is easier to make to higher optical standards. Neither is factual - Maksutov corrector is not perfect optically, and is all but easy to make - and if there is a particular reason that it performs better, it is in the above average fabrication quality.

It could be that it is exactly the high required fabrication accuracy that resulted in the above average fabrication quality of the Maksutovs'. The tolerances are very narrow, and the manufacturer cannot allow for the luxury of relaxed fabrication/control, if planning on any kind of success on the market. On the other hand, it is the labour-intensive nature that allows achieving very small changes in radius - in the end it boils down to being familiar with the proper grinding/polishing technique and testing accuracy.

Similarly to the Schmidt-Newtonian, the only difference between the camera and telescope arrangement with Maksutov corrector in the Newtonian configuration comes from the corrector's position. In the Maksutov-Newtonian, the meniscus is closer to the spherical primary, commonly inside its focal point. Corrector position usually nearly coincides with the aperture stop, so that reduction in mirror's off-axis aberrations is very similar to that in the Schmidt-Newtonian. However, unlike the Schmidt corrector, the meniscus induces some coma and astigmatism of its own, which makes the final system properties somewhat different. System properties in the Newtonian configuration with spherical primary (FIG. 184) can be quite well approximated based on the mirror/meniscus combination described in the previous section.

FIGURE 184: Illustration of the Maksutov-Newtonian telescope configuration. The primary is spherical, and the corrector lens is at ~0.8 of the primary's focal length in front of it. Aperture stop at the corrector reduces mirror coma by ~40%. About half of the remaining mirror coma is cancelled by the offset with the opposite coma of the corrector. That puts the coma of a typical MNT at ~30% of that of a comparable Newtonian. Astigmatism and field curvature in Maksutov-Newtonian are also lower, mostly due to the effect of displaced aperture stop.

With σ~0.43, according to Eq. 131, coma is reduced to ~30% of that in a comparable paraboloid (note that with the meniscus convex to outside its coma changes sign, and adds to that of the primary; in such arrangement, this system would have nearly twice as much coma). Somewhat lower astigmatism - mostly due to the aperture stop being displaced from the spherical primary, and the rest due to the offset by the opposite astigmatism of the corrector - results in less than half as strongly curved median image surface. Spherical aberration cannot be reduced to zero, as it can - at least in the design stage - with the comparable Schmidt corrector, but the correction level is still impeccable at ~f/4 and smaller relative apertures, and the chromatism is, for all practical purposes, non-existent (FIG. 185).

As a consequence of the corrector being closer to the mirror, its effective power for the mirror is slightly higher. In other words, the corrector's spherical aberration contribution is slightly higher. Since the mirror contribution is unchanged, in order to strike the optimum balance between the two, radii of the corrector need to be slightly more relaxed than in the camera arrangement. Reflecting this, the first corrector radius is better approximated by R1~[1-2τ-(F/100)]R"1, than as given with Eq. 128.

FIGURE 185: Ray spot diagrams for 200mm f/4 Maksutov- and Schmidt-Newtonian, for (from left) the violet (436nm), blue (486nm), green (546nm), red C (654nm) and h (707nm) spectral lines. Seemingly greater axial chromatism (secondary spectrum) in the MN is actually its residual higher-order spherical aberration (not correctable in an all-spherical system, but reduced to only 1/80 wave RMS here by balancing it with primary spherical). On the other hand, in the Schmidt-Newtonian chromatc error nearly entirely stems from spherochromatism. Closer look at the OPD (optical path difference, i.e. wavefront error) reveals that the chromatic error is slightly greater in the MN (the PSFs shown are for the violet g-line). However, in either system axial chromatism is, for all practical purposes, non-existent. Some lateral chromatism is noticeable in the MN, insignificant visually, and acceptable for most photographic purposes. Both systems have inferior field performance to that of comparable Houghton-Newtonian varieties (FIG. 130 a/b). Astigmatism is similar in both, near negligible: 0.025mm longitudinal astigmatism at 0.5 degrees off axis translates into 0.025/8F^2=0.000195mm P-V wavefront error, or 0.36 wave for 0.00055mm wavelength - just a tad better than the "diffraction limited" 0.0745 wave RMS (astigmatism plot originates in the paraxial focus - hence it's shifted from the best focus in the MN - since the wavefront deviation is measured vs. central portion of the wavefront, focusing at the paraxial focus). Unlike the SN, Maksutov-Newtonians typically have a small central obstruction, around 0.2D, with near-negligible effect, and a slower focal ratio. SPEC'S: MN SN

Similarly to the Schmidt-Newtonian, alignment of the Maksutov-Newtonian is more complex than that of all-reflecting Newtonian, due to the presence of lens corrector. Ray tracing indicates that sensitivity to decenter of the Maksutov corrector is similar to that of the Schmidt; however, its sensitivity to tilt is several times higher. Raytracing a more common 6-inch f/6 configuration (below) illustrates aberrations arising from misaligned meniscus (the two mirrors simply cause the field to shift with respect to the apparent field center, w/o creating any aberrations). In other words, field created by the meniscus misalignment will be in effect shifted by misaligned mirrors and/or focuser. That could be either compensatory, or additive. Note that the ray spot plots are for flat field, since field aberrations are slightly lower than for the best astigmatic - i.e. curved - field, due to the presence of coma.

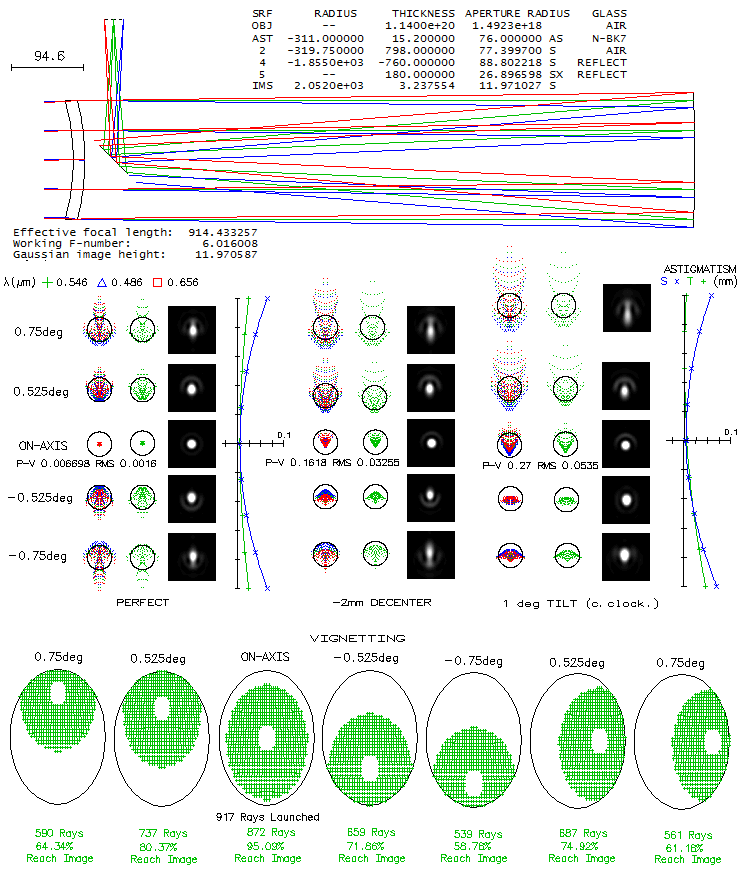
Decentering meniscus by 2mm down brings 1/6.2 waves P-V of coma to the field center, with the best focus shifted 0.2° down (1/80 wave RMS of asymmetrical aberration consisting mainly from Zernike defocus and coma). Meniscus tilt of 1° counterclockwise (top away from the primary) induces 0.27 wave P-V of coma to the field center, with the best focus point shifted about 0.3° down (1/40 wave RMS of Zernike defocus and coma). Best focus section extends to about 0.15° gradually worsening after that. Either decenter or tilt cause astigmatic field to become asymmetrical, with sagittal astigmatism decreasing in the upper field, and increasing in the lower (a bit less with the decenter than with the - shown - tilt). This in effect creates image tilt that can become significant with more of misalignment. Coma induced by misalignment is approximately in inverse proportion to the 3rd power of focal ratio: at f/4, this same amount of decenter would induce 1/2, and tilt 2/3 wave P-V of coma to the field center.

Vignetting at the diagonal (bottom) is with 36mm diagonal minor aixis, w/o offset. Out of 917 rays launched 872, or 95% makes it past central obstruction (it should be closer to 94%, but accuracy is less than 100% due to the limited number of rays). Considering that, vignetting of the 0.75° beam ranges from 38% at the diagonal's bottom to 33% at the top (24% and 16% for the 0.525° beam, respectively).

◄ 10.2.3.1. Approximating corrector radii ▐ 10.2.3.3. Maksutov-Cassegrain ►

Home | Comments