◄ 7.3. Apodizing mask   ▐    8.1.1. Newtonian off-axis aberrations ►

With distortion being zero for the stop at surface, remaining primary aberrations are spherical, coma, astigmatism and field curvature. A quick look at the aberration coefficients gives following wavefront errors for the concave mirror:

as the P-V wavefront error at the best focus (1/4 of the error at paraxial focus), with K being the mirror conic, D the aperture diameter and F the focal ratio. Evidently, the only surface form free from spherical aberration for object at infinity is a paraboloid (K=-1). The RMS wavefront error for primary spherical aberration is smaller than the P-V error by a constant ratio; it is given by ω=W/1.5√5 , or: 

In units of the λ=0.00055mm wavelength, the P-V wavefront error is:

for the aperture D in mm, and in inches, respectively, with the corresponding RMS wavefront error ω=W/√11.25.

Longitudinal and transverse aberrations are as given in 2.1 Spherical aberration. The RMS wavefront error, in units of the wavelength, can be used to calculate the appropriate Strehl ratio from Mahajan's close approximation (Eq. 56). For spherical mirror, it can also be expressed as:

for the natural logarithm base e~2.718, and the aperture diameter D in mm. Taking conventional 0.80 Strehl, or the RMS wavefront error in units of the wavelength ω=1/√180 as the maximum acceptable amount of wavefront degradation, sets the appropriate F# limit for spherical mirror at F=(3.55D)1/3 or larger for D in mm, and
F=(90.17D)1/3 for D in inches. Counting in the effect of central obstruction, the criterion becomes more demanding, as described in 5. Obstruction effects.

From  S~1-(2π ω)2 , needed F# for a desired Strehl S with spherical mirror is given by F~3.5D1/3 /(1-S)1/6 , for the aperture diameter D in inches, and F~1.18D 1/3 /(1-S)1/6 for D in mm (since based on the approximation, it is accurate for Strehl ratios of ~0.9 and higher; for the ratios ~0.8 and lower, it gives increasingly higher F# than the actual value).

For objects close enough that the primary magnification m, defined as one of Eq. 9 parameters, appreciably differs from zero, the P-V wavefront error at the best focus, after substituting for m in terms of the object distance o and mirror focal length f, is W's =-[K+(1-2ψ)2]D/2048F3 (the minus sign indicating the aberration is numerically negative at the best focus location; consequently, it is positive, or overcorrected at paraxial focus), with ψ=f/o being the primary focal length in units of the object distance (the reciprocal of the object distance in units of the mirror focal length). Obviously, the wavefront error is zero if the expression in the brackets is zero, which defines the zero-aberration conic in terms of object distance, for primary spherical aberration, as K=-(1-2ψ)2 .

Inversely, object distance in terms of wavefront error induced can be written as (1-2ψ)2=[2048WF3/D]-K. For the wavefront error in units of 550nm wavelength, it is (1-2ψ)2 =-[1.126WF3/D]-K. For a selected wavefront error, the right side gives the value of (1-2ψ) squared, which makes finding ψ easy. For instance, for W=0.05 wave in units of 550nm wavelength, D=400mm f/4 paraboloidal mirror (thus F=4 and K=-1), the value of (1-2ψ)2 is 0.99099, thus (1-2ψ)=0.99549 and ψ=(1-0.99549)/2=0.00226. The corresponding distance is f/0.00226=443f=708.9 meters, nearly identical to the value obtained with somewhat rounded off relation given in the section on star testing.

Most Newtonian telescopes nowadays use paraboloidal primary. If well made, its spherical aberration is practically cancelled. However, off-axis aberrations are present, and can be significant - particularly coma. Before addressing full aperture off axis aberrations of a Newtonian, a quick look at the effect of off-axis mask, in a fairly common use with larger instruments of this kind.
 

EFFECTS OF OFF AXIS MASK

With off axis mask on, light effectively uses off-axis section of a paraboloid. This causes: (1)reduction in the level of off axis aberration, which is also from dominant coma transformed to dominant - although still somewhat coma-like in appearance - astigmatism, and (2) tilted best image surface. In the case shown, a large 560mm f/3.6 mirror, with a 200mm mask opening, tilt is significant enough to cause deformation of the diffraction image farther off axis (1.5mm of tilt-caused defocus at 17.5mm radius corresponds to 100mm field curvature radius, thus requires significant eye accommodation). The field is also asymmetrical, with the astigmatism along the tilted (vertical) radius having different form than along the horizontal field radius.

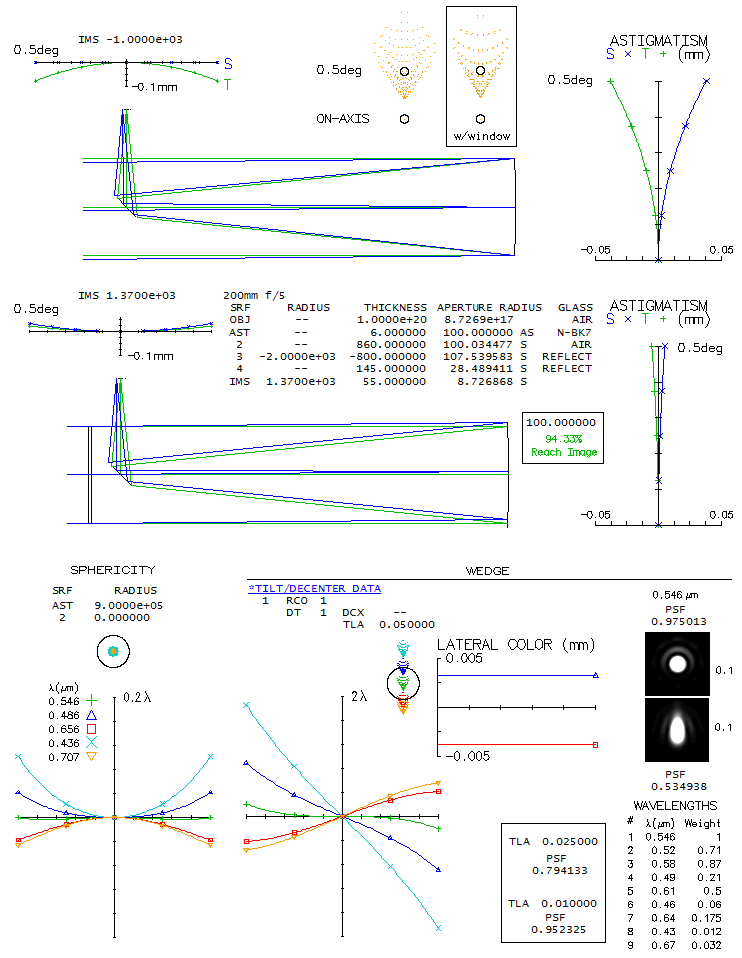
Mask distance has a minor influence on the magnitude of off axis aberration. Since this astigmatism originates in the mirror coma, it also changes with the field radius. Placing mask farther away increases the chief ray height at the mirror, increasing by it off axis error. As a relative aberration, in units of the aberration with the mask at the mirror surface, the increase is approximated as 1+αS/[29(D-M)], where α is the off axis angle in degrees, S is the mirror-to-mask separation, D is the mirror diameter and M is the mask opening diameter. In this case, α=0.5, S=1600mm, D=560mm, M=200mm, and the relative aberration is 1.077 times larger than with the mask at the mirror.

OPTICAL WINDOW EFFECT

While not widespread among amateurs, and pretty much ignored by the commercial makers, sealing off a tube of the Newtonian by placing optical window on its front end seems to keep its appeal for at least a few. The benefits are avoiding spider vanes diffraction and protecting the tube inside and primary from dust and impurities contained in the air. Does such window produce optical effects, and how accurately made it needs to be in order not to induce significant aberrations?

To find the answers, will raytrace a 200mm f/5 Newtonian (below). Configuration is more or less standard, and small differences will not significantly effect results. Unavoidable effect, which is not even caused by the window itself, rather by placing aperture stop at a distance from the primary mirror, is change in off axis astigmatism, and wit it in the field curvature. As raytrace for arrangements without (top) and with optical window (below it) show, stop shift significantly reduced astigmatism, making best image surface somewhat more relaxed, and with the curvature of opposite sign than that with the stop at the mirror. While in the latter best image radius (absolute value) equals mirror's focal length and is concave toward mirror, with the window on best image radius is 1370mm, convex toward mirror (if astigmatism would go to zero, image field radius would equal Petzval curvature, i.e. one half of the mirror surface curvature radius. With the new stop location, longitudinal astigmatism at 0.5° is reduced from nearly 0.08mm to 0.012mm (since the P-V error is - same as for defocus - smaller by 8F², from 0.7 to 0.1 wave P-V, respectively, for 550nm wavelength). Despite the significant reduction in astigmatism, off axis blur at 0.5° is little changed, due to the coma accounting for most of the blurring (about 2.4 waves P-V). If the window clear opening equals that of the mirror, some vignetting is induced: less than 6% at 0.5° and twice as much at 1° off (for zero vignetting, mirror radius needs to be 7.5mm/15mm larger).

As for the effects of the window itself, first about what don't cause any: its thickness, and possible tilt (without going to extremes, of course). The window is very forgiving with respect to near-spherical deformation of its surfaces. As much as 10 waves deep deformation would induce as little as 1/25 wave P-V in the blue (F) and red (C) lines, with entirely negligible spherical aberration in the central line (bottom left). Twice as deep deformation would induce twice more of each, and so would the same magnitude deformation on both window surfaces. This means that for approaching the "true apo" level the window would need five times deeper sphericity (50 waves, or 0.0275mm) on its one surface, or half as much on each of the two. No lateral color, or other aberrations are induced.

It becomes much less forgiving when it comes to wedge error. As little as 1/20 of a degree tilt of one of the surfaces (in this case the front surface, tilted counterclockwise, with the top point 0.175mm farther out than the bottom) would induce all-field lateral color separating F and C lines at a distance about equaling the Airy disc diameter, amounting to 0.9 wave P-V in the F, and half as much in the C (bottom right). The center field coma induced is still very low, causing 0.975 Strehl degradation. But the lateral color error causes polychromatic Strehl (430-670nm, photopic sensitivity) to drop to 0.53. Half as strong wedge - causing half as much of lateral color error - would still limit the poly-Strehl to 0.8. For reaching 0.95 poly-Strehl, i.e. 1/8 wave P-V of spherical aberration level - wedge error would have to be yet another 2.5 times smaller, or 1/100 degree (0.035mm).

Internal glass strains can induce significant large-scale wavefront deformations, and impurities/inhomogeneity will induce small-scale wavefront deformation and scattering. To avoid this, the window should be made from a quality optical glass.

◄ 7.3. Apodizing mask   ▐    8.1.1. Newtonian off-axis aberrations ►

Home  |  Comments