|
telescopeѲptics.net ▪ ▪ ▪ ▪ ▪▪▪▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ CONTENTS
7.3. APODIZING MASK FOR TELESCOPES
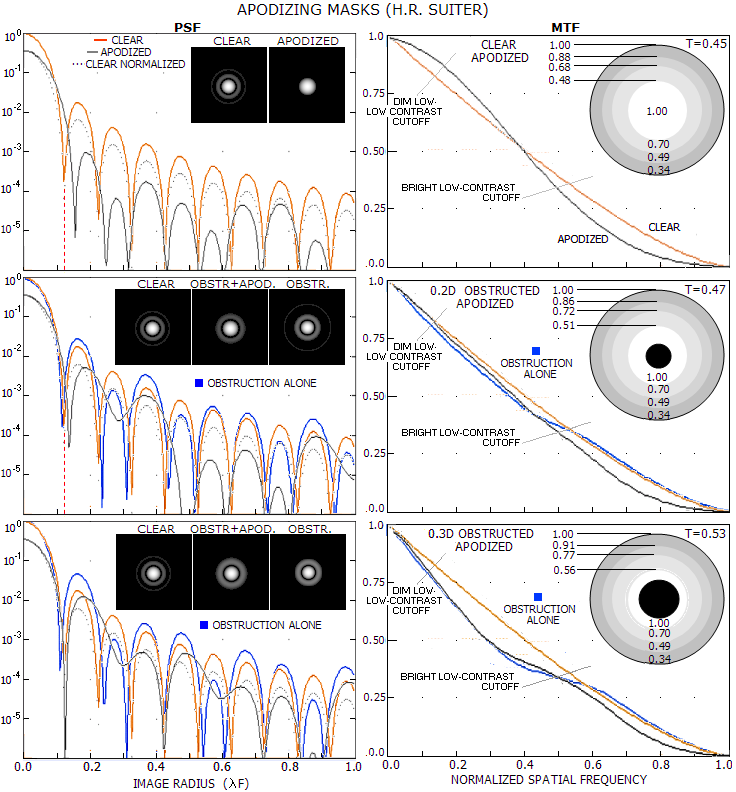
PAGE HIGHLIGHTS Apodizing, or change of aperture's transmission properties, also affects intensity distribution within the diffraction pattern it generates. The effect of apodization was mainly subject of speculations among amateur astronomers, until Harold R. Suiter published his book and articles, during the 1990s and at the beginning of this century, using diffraction calculation to find specific answers. This text uses his analysis and his diffraction program "Aperture", with somewhat expanded coverage of the effect of Gaussian apodization and potentially useful types of apodizing masks. There is a number of possible patterns of altering pupil light transmission. The starting point here is so called Gaussian pupil, where the change in wave amplitude over the pupil follows a Gaussian function (FIG. 111A).
Gaussian amplitude profile over the pupil has full amplitude (A=1) in the center, decreasing toward the edge. The smaller Gaussian width w, the greater amplitude suppression toward pupil edge, the wider central diffraction maxima, and the fainter ring structure. Amplitude profiles and corresponding PSF simulations are shown for w=∞ (uniform transmission), 1.5, 1, 0.7 and 0.4. As the plots below show, ring structure is nearly non existent at w~0.7, and further suppression of amplitude in the outer area mainly achieves significant central maxima expansion. So for an apodizing mask of this type the optimum Gaussian radius is w~0.7. With incoherent light, total energy in the pupil - or transmission - is proportional to the amplitude squared. Squaring, in effect, produces a narrower Gaussian, whose volume vs. volume of the cylinder equals the transmission coefficient (top right). For w=∞, 1.5, 1, 0.7 and 0.4 total transmission is 1, 0.663, 0.432, 0.241 and 0.080, respectively.
The two main opposing effects of this type of pupil apodizing are:
The encircled energy plots show that the relative energy within 1.22λF radius steadily increases from 84% for uniform pupil to 97% for w=0.7 Gaussian, which has less than 1% of energy outside its central maxima. Again, further reduction in the value of w does not seem justified, at least for general purpose. MTF plots (bottom) illustrate the gain, and the loss due to pupil apodization. Vanishing rings energy results in better contrast over low-to-mid MTF frequencies. Expanding central maxima, however, lowers it over mid-to-high frequency range. At w~1, the gain and loss are visually near equal; loss is already significantly larger nominally but, on the other hand, the mid-to-low frequency range covers much wider variety of details of about Airy disc in size and larger. This implies that somewhat greater reduction in w could still be worthwhile from the practical point of view. But even at its best, the gain in mid-to-low frequency range is relatively small. It is comparable to the gain of going from 1/6 wave P-V wavefront error of balanced primary spherical aberration to zero-aberration aperture, or from 0.91 Strehl to 1. And the price to pay is nominally significantly greater contrast loss in the high frequency range, including loss in threshold resolution for bright low-contrast (e.g. planetary) details.
The contrast transfer consideration in FIG. 111A strictly applies to the standard MTF pattern, i.e. one with sinusoidal intensity distribution. In general, there is no major difference if square-wave pattern, with evenly bright and dark bars is used, except that contrast transfer for the latter is somewhat higher over the range of frequencies. It can be concluded that Gaussian pupil is more useful in observing low contrast detail, either bright or dim, since contrast gain due to it covers most of the resolvable range for this detail type. However, this gain is likely to come at a price of somewhat compromised threshold resolution for this type of details. Independently of its effect on contrast transfer, the effect of Gaussian apodization on suppressing diffraction rings - and primarily the first bright ring - is beneficial in resolving, or detecting faint companions positioned in the first bright ring of the principal star. Another benefit from Gaussian apodization is that it generally increases the tolerance for inherent system aberrations. In other words, it does reduce the negative effect of any given level of conic surface aberrations - spherical, coma, astigmatism - as well as the effect of defocus. In the systems with relatively significant inherent aberrations - particularly astigmatism - it can produce noticeable improvement in the performance level based on this factor alone. Apodization is even more effective in suppressing the effects of local/zonal surface errors affecting the extreme outer area of the wavefront , such as turned edge. And, it is always important to consider the actual conditions of use. As Suiter points out, seeing error generally worsens contrast and resolution in the high-frequency MTF range. In larger amateurs apertures, details in this range are observable only in a fraction of the time, at best (FIG. 92B). In such case, there is little or no harm from the nominal contrast drop in this range, but the advantage of improved contrast in the mid-to-low frequency range remains.
Apodizing mask
Practical problem with Gaussian pupils is that fabricating substrate
producing such an accurate fall off in pupil amplitude/transmission requires complex
technology, generally unavailable to the amateurs. Suiter solves that
problem by designing step-apodizers made of a widely available material,
an ordinary window screen (FIG. 111B).
In general, this step apodizer will produce similar effect to that of
Gaussian pupil transmission it is comparable to with respect to the
average drop off toward the pupil edge. There is an important difference
between the two, and it is that step apodizer does not affect amplitude
of individual waves - it selectively blocks them, or transmits. In
coherent light, it would produce reduction in the complex amplitude
(i.e. the sum of individual wave amplitudes) proportional to the pupil
area blocked in the total area, with the energy (light transmission)
proportional to this relative area squared. For instance, a mask
blocking half of the pupil area would reduce the energy fourfold.
In incoherent light - which is closer to the kind of light coming from
astronomical objects - the energy is a sum of squared individual wave
amplitudes. Hence energy transmission is proportional to the clear pupil
area: blocking half of it will have it reduced twofold. More important,
however, is that this different dependence of the energy on the aperture
area would cause differences in point-source PSF, hence in the
corresponding MTF as well. Similarly to case of the effect of
central obstruction, the effect of
apodizing mask should be significantly smaller in incoherent light,
where the blocked out energy is deducted directly at the level of
energy, not at the level of amplitude.
The diffraction relation used by Suiter is from the domain of
conventional treatment of diffraction effects, assuming
near-monochromatic - in effect coherent - point source. And so is,
according to its output, the underlying algorithm used by OSLO. If so,
effects of pupil apodizing in the actual use by amateurs are
significantly weaker than these shown, although they should be generally
similar in their form. In other words, it would require significantly
stronger apodizing in incoherent light to achieve effects shown here in
incoherent light.
With this in mind, follows an overview of some basic principles in
designing apodizing mask, and the effect of varying parameters of its
simplest configurations.
Starting with the Gaussian transmission curves above, a simpler, nearly as
effective apodizers can be put together as well (FIG. 111C).
Additional purpose is to illustrate the degree of change in the
diffraction effect as a result of different mask shading patterns.
Unfortunately, but expected, the beneficial effect of these masks also
diminishes with the increase in central obstruction.
Some simple narrow-purpose mask profiles would include those with a
single-layer screen zone featuring a concentric ring with further
reduced transmission. In general, a darkened, or opaque ring in the
outer pupil area tends to reduce brightness of the first 2-3 bright
rings, but at the price of shifting significant portion of energy to the
rings farther out. Multiple rings have similar effect. If properly
designed, such mask can shift the energy far from the central maxima,
with little or no ill effect on contrast in the actual observing, while
benefiting from the darkened close rings. Unfortunately, that also comes
at the price of enlarged central maxima.
In all, apodizing mask can produce effects beneficial
for observing extended details larger than roughly twice the stellar
resolution limit. It is not dramatic: generally less than the benefit of
correcting 1/4 wave P-V of spherical aberration, but it is easy to
employ and deploy, and every little bit can count. Apodizer can also be
helpful in resolving close unequal doubles, with the faint companion
situated in the first bright ring of the principal star. These
beneficial effects, however, come at a price of contrast loss with
details close and at the limit of resolution. In general, benefits of
apodizing are greater for larger apertures, which are due to the larger
seeing error typically able to resolve only details in their mid-to-low
frequency range. Finally, apodizing mask will have little effect in
apertures with central obstruction significantly larger than 0.2D.
One of the constant desires of some amateur astronomers - along with taming
the secondary spectrum in achromats - is how to make diffraction spikes produced
by spider vanes disapear. Those that are for any reason not satisfied
with curved vanes spider varieties, keep turning toward vane apodizers, i.e.
vane masks of a form that will not produce visible spikes. I've put two
apodizers that have acceptable obstruction added through OSLO, and below
are the results. In fact, only one of the two adds acceptable obstruction;
it is described in a scientific-looking
PDF file, but it's claims appear
not to be quite substantiated (bottom).
The other one was empirically proven to work as
intended, but the side effects of added obscuration were noticed (top).
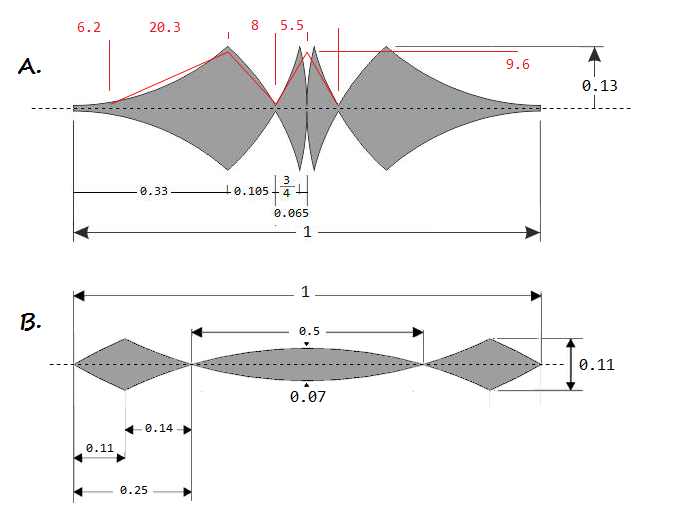
Given are dimensions normalized to the length as unity, actual shape, and
closely approximated shape as entered in raytrace (the bottom apodizer is nearly
identical to its original shape, the only difference - and rather negligible - is that its diamond-like
ends are entered as quadrangles). Differences vs. actual shape can be
considered negligible to the diffraction effect. Below are diffraction patterns
produced by raytrace (OSLO Edu), along with the MTF showing contrast transfer
for the 20% central obstruction alone (goes as diffraction limit), and with the
apodizer added (diffraction patterns are normalized to 1% of the central
intensity, hence all areas brighter than that are uniformly white).
The effect of a conventional thin-vane spider would be
yet significantly smaller than that of the apodizer, and isn't shown.
Picture below shows diffraction effect of several more different apodizers.
It should help understand what is needed to eliminate spikes, as well as
give some basic insights in the "mechanism" of diffraction.
Top row shows that apodizer made of lined up circular discs of the same
size does very little to suppress spikes versus a plane 4-vane spider of
equal area (left). Replacing circles with squares lined up diagonally
has noticeable more of an effect (next), and it further increases if the
squares are of unequal size (right). On the bottom, apodizers in an elongated
triangular form produce markedly different effect with different orientation (left),
even if their diffraction pattern - when treated as inverse aperture, whose
energy is deduced from the energy of the underlying diffraction pattern of the
aperture - does not change with their orientation (right).
The reason is that what produces the effect is the entire obsctruction shape,
i.e. the effect is not a simple sum of the effects of its constituents (bottom right).
Simple conclusion is that in order for an apodizer to eliminate spikes, it
has to sufficiently brake away from the plane vane form.
|
So
far, it was assumed that the optical system with Gaussian pupil
transmission is aberration-free. In the presence of aberrations,
Gaussian transmission gradient over the pupil does not influence shape
of the wavefront, but does influence the magnitude of wave contributions
from different portions of the pupil. In general, contribution
suppression increases toward the edge. If those portions of the
wavefront are aberrated, it will reduce their destructive contribution.
Graph at left shows how the four principal aberrations - spherical,
coma, astigmatism and defocus - given in unit value for even pupil
transmission, decrease with the Gaussian width w. Expectedly, the
two aberrations that peak toward pupil edge over all, or significant
portion of the outer wavefront area - astigmatism and defocus - are
reduced the most. At w=0.7, the reduction is 0.92, 0.89, 0.74 and 0.72
for spherical aberration, coma, astigmatism and defocus, respectively.
If there are two or more aberrations present, the combined reduction is
greater than for any single aberration. As the negative effects of apodization quickly increase with further reduction in
w, this is
probably close to the maximum benefit achievable with apodization in this
respect.
