|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
8.3.1. Paul-Baker, flat-field
anastigmatic aplanats
▐
8.4.2. Two-mirror TCT
► 8.4. Off-axis and tilted component telescopes; Herschelian reflectorAxially symmetric reflective telescopes
have disadvantage of the smaller mirror being in the light path,
causing additional diffraction effect degrading image quality. In order to avoid it, one or more mirrors
either have to be tilted, or made as an off-axis segment of a
larger system. Mirror tilt induces severe coma and astigmatism,
hard to control, except at relatively small apertures. Off-axis systems,
on the other side, have better control of aberrations, but are limited
in size by production difficulties and/or price. Consequently, both, tilted
optics and
8.4.1. Herschelian reflector
The
simplest unobstructed reflecting system is so-called Herschelian
reflector, used by the great German/British astronomer of the
late 18th and early 19th century, Sir William Herschel. In order to
prevent additional light loss on an extra mirror surface of - back then
- very low reflectivity, Herschel tilted the primary enough to bring the
focus out of incoming light, with the eyepiece mounted on the side of an oversized tube.
While it eliminates central obstruction effect and the light loss, mirror tilt
results in significant image deterioration. It is possible that Herschel
partly corrected for it by tilting the eyepiece, but the design still
suffers from aberrations, as well as air turbulence caused by warmth off
the observers head, placed next to the path of the incoming air. The
more recent variant, with the side flat mirror directing image plane away
from the tube eliminates that problem (FIG. 132), but a very long-focus
mirror is still required in order to keep aberrations at an acceptable
level.
Small long-focus mirrors can be left spherical, since their spherical aberration is negligible. However, the tilt-induced center-field astigmatism and coma still can cause unacceptable image deterioration. The mirror tilt angle τ will result in the P-V wavefront error of astigmatism Wa=τ2D/8F (from Eq. 18), and the coma P-V wavefront error of Wc=τD/48F2 (from Eq. 12-15.1), both at their respective diffraction foci. If ζ is the relative distance in units of the primary focal length at which the ray reflected from the mirror center breaks out of the path of incoming axial pencil (FIG. 85), then the tilt angle τ=1/4ζF in radians, and the two can be written as:
Wa=D/128ζ2F3
and
Wc=D/192ζF3. (93)
D being the aperture diameter and
F the focal ratio. Setting the minimum flat separation at
1" between the incoming axial pencil and the flat center point (giving
~1" usable field diameter), the relative distance ζ is given by
ζ=(f-D-4)/(D+2)F with
f, D and F being the mirror
focal length, diameter (in inches) and focal ratio, respectively.
For mm, ζ=(f-D-100)/(D+50)F. Between 100mm
f/20 and 150mm
f/25, ζ
varies from 0.6 to 0.7, respectively.
Since ζ<1, Eq. 93 indicates that the astigmatism is dominant, with the
P-V wavefront error
larger by a factor of 1.5/ζ than that for the coma. To make them comparable, the
two P-V
errors need
to be expressed as RMS, which are smaller by a factor
of √24
and √32
for astigmatism and coma, respectively. Then, needed mirror focal ratio F for any given RMS wavefront error ωa
of astigmatism introduced to the field center is given by
For D=100mm aperture diameter, ζ=0.6 and ωa=λ/14
(λ=0.00055mm),
needed focal ratio F=22.3. For these values of D, ζ and
F,
the coma RMS wavefront error is λ/40. Assuming the two mostly unrelated,
the combined RMS wavefront error approximation, from the square root of
the sum of errors squared, comes to ~λ/13.2. Still slightly below the 0.80
Strehl standard (λ/13.4) in the field center, but it
does exceed this level in the best portion of the
field (FIG. 133). Since the tilt angle
τ=1.2°, at 0.2° off-center in
the direction of mirror tilt, the actual incoming pencil angle is 1°,
reducing the astigmatism wavefront error by a factor of 0.7 and coma by
a factor 0.83, for the combined error of ~λ/18.5 wave RMS, and
corresponding 0.89 Strehl.
The wavefront error of a tilted
concave mirror can also be expressed in terms of the mirror tilt
τ in
degrees. For the aperture D in mm, the astigmatism RMS
wavefront error in units of 550nm wavelength is given by wa~Dτ2/71.4F,
and that for the coma by wc~Dτ/8.6F2.
For D in inches, wa~Dτ2/2.8F,
and wc~3Dτ/F2
(expressions are slightly rounded, but accurate to within a couple
of percent).
Herschelian-type telescope can gain
significantly in correction level, compactness, aperture size and/or
relative aperture if some type of lens corrector is used to minimize
tilt-induced aberrations. The usual choice is wedged lens, or wedged
meniscus, inserted at an angle to the axis in the optical path in
the converging light cone. A single BK7 meniscus with unequal radii
(R1=80mm,
R2=88.4mm,
concave toward mirror, 9.8mm center thickness, front surface at
1450mm from mirror vertex, 3.8mm positive vertical axial decenter),
reduces center-field aberration of a 2.3° tilted 200mm diameter f/8
sphere to 0.042 wave RMS. Despite some lateral color, it makes for
quite useable unobstructed aperture, with better part of its strong
field astigmatism offset by astigmatism of the eyepiece. Better
results are possible with more sophisticated - and complex -
corrective lenses.
The question is, is there a practical benefit
from it? What is common to all these compensating lens correctors is
that they have very tight tolerances for spacing, tilt angle,
surface curvature and center thickness, due to an enormous load of
compensatory aberrations (mainly astigmatism). It requires very
accurate mounting and adjustment mechanism, and even then it is
questionable how close to its optimum such a system can be
objectively maintained.
On the other hand, a
200mm f/8 mirror in a regular Newtonian
arrangement can work with central obstruction in the 0.15 to 0.25 of
the aperture diameter range, satisfying requirements from high-contrast
planetary to a wider illuminated field deep-sky instrument. Its
particular advantage is comparatively low sensitivity to
misalignment, thus likely better field performance than what optical
data per se indicates. Considering this, a tilted-mirror telescope
is an alternative mainly for those who find in it values other than
its optical quality and practicality of use.
Catadioptric Herschelian
with full aperture Houghton corrector
A catadioptric variant of
Herschelian that offers good overall correction, while making possible
to use significantly faster mirror, uses the simplest form of a
zero-power Houghton corrector: two full aperture plano (PCX and PCV)
lenses of equal radii placed at nearly the focal length separation in
front of the mirror. This is a slightly modified design originally
proposed by D. Shafer (Telescope Making 41, as presented in "Reflective
and catadioptric objectives" chapter by Lloyd Jones, University of
Arizona). It is an all-spherical 150mm
f/8
system.
The two tilted elements are the rear lens and the mirror. Correction of
aberrations is very good over flat field, with the diffraction field
diameter exceeding 1 degree. Axial chromatism easily passes the "true
apo" requirement; Lateral color is well controlled, with all the
wavelengths remaining within the Airy disc. Image tilt (about 5.5° with
left side being lower than the right side on the system diagram shown),
results in 3.6 waves of defocus at 0.5° field angle. Linearly, it
is nearly 1mm away from the plane containing field center. Since that
field height (10-11 mm) corresponds to the field edge in a standard 20mm Plossl,
the accommodation required is nearly 2.5 diopters (from one diopter
of accommodation given by f2/1000, f being the
eyepiece focal length), or from infinity to 0.4m. However, required
field edge accommodation would
double with 10mm f.l. eyepiece, which is still only a medium magnification
range for the aperture. Note that the above system is not
fully optimized, so nearly all aberrations can be a bit lower, but it
wouldn't bring tangible practical gains.
For the system to approach its design correction level, the two tilted
elements have to meet very tight tolerances, with respect to the tilt
angle. Also all three elements (the diagonal flat is optional, and
optically passive) have to be very well centered around optical axis. In
other words, this system requires a high quality mechanical assembly -
optical tube in general, and lens and mirror cells in particular.
|
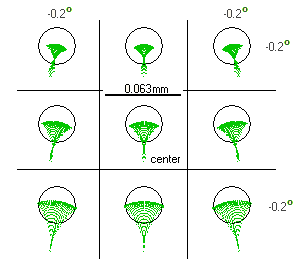 FIGURE
133: Ray spot diagram for
a 100mm f/22.3 Herschelian with the mirror tilt
τ=0.021
radians (1.2°). The circle represents the Airy disc diameter. The
field is aberrated asymmetrically, due to the wavefronts coming at
the mirror from the direction of the tilt finding it inclined at a
smaller angle than wavefronts coming from the radially opposite
direction. The aberration diminishes going from the field center in
the direction of mirror tilt (which is toward the location of the
flat mirror ). The size of
aberration is fairly sensitive to changes in the mirror
F-number. Neglecting the change in ζ
as relatively insignificant compared to change in the ratio number F,
from Eq.93, to a first approximation the wavefront
error for both, coma and astigmatism changes in inverse proportion to the cube of F- number.
Thus,
10% slower mirror
would have the aberrations lower by a factor of ~0.7. On the other hand,
relatively small 10% gain in shortening the focal length would come
at the price of both aberrations increased by about a third. As with
all tilted-mirror systems, the image field is also tilted, although
with the effect being negligible due to usually very low tilt
angles. The field center aberrations are comparable to the effect of
33% central obstruction.
FIGURE
133: Ray spot diagram for
a 100mm f/22.3 Herschelian with the mirror tilt
τ=0.021
radians (1.2°). The circle represents the Airy disc diameter. The
field is aberrated asymmetrically, due to the wavefronts coming at
the mirror from the direction of the tilt finding it inclined at a
smaller angle than wavefronts coming from the radially opposite
direction. The aberration diminishes going from the field center in
the direction of mirror tilt (which is toward the location of the
flat mirror ). The size of
aberration is fairly sensitive to changes in the mirror
F-number. Neglecting the change in ζ
as relatively insignificant compared to change in the ratio number F,
from Eq.93, to a first approximation the wavefront
error for both, coma and astigmatism changes in inverse proportion to the cube of F- number.
Thus,
10% slower mirror
would have the aberrations lower by a factor of ~0.7. On the other hand,
relatively small 10% gain in shortening the focal length would come
at the price of both aberrations increased by about a third. As with
all tilted-mirror systems, the image field is also tilted, although
with the effect being negligible due to usually very low tilt
angles. The field center aberrations are comparable to the effect of
33% central obstruction.