3.3.2. Aberrations of the conic surface

While the conics are free from spherical aberration when the object is located at either of the two specific conjugates (foci), it is not the case with the rest of aberrations. For off-axis points, incident wavefronts are at an angle to the surface, which results in loss of symmetry needed for the formation of a perfect spherical wavefront. Thus all conic surfaces of revolution - sphere, ellipses, parabola and hyperbolas - suffer from coma and astigmatism, which are independent of the conic for the stop at the surface and object at infinity. And when the object is not in one of the two specific conic conjugates, it will also suffer from spherical aberration.

Since aberrations inherent to conical surfaces vary, in general, with their eccentricity, degree and sign of curvature, object distance, as well as the entrance pupil location, two or more surfaces can be combined in order to minimize or cancel the final aberration.

PRIMARY ABERRATIONS

In all, there is five intrinsic primary telescope aberrations characteristic of a conic surface of revolution:

- spherical aberration
    - coma
    - astigmatism
    - field curvature, and
    - distortion

Only spherical aberration is an axial aberration; the rest of them are off-axis, or field aberrations. The first three aberrations - spherical, coma and astigmatism - are a result of wavefront deviations from spherical, hence they affect energy distribution in the diffraction image - that is, point-object image quality (FIG. 24). The last two - field curvature and distortion - are caused by variations in wavefront radius or tilt angle with the point height in the image space, thus affecting image form.

FIGURE 24: The three primary, or Seidel aberrations affecting point-image quality. Spherical aberration is radially symmetrical wavefront deviation, making it progressively more strongly curved toward the edges, than a reference sphere centered at paraxial (Gaussian) focus G. It occurs whenever object imaged is not located at one of the two specific foci of a conic. It is illustrated on the spherical reflecting surface imaging distant object. As waves arrive at the mirror surface, its atoms begin to absorb and re-emit waves in all directions. Change in the sagitta of spherical surface (∆) determines surface slope, which reshapes the flat incoming wavefront (FIG. 3) into a curved one, curving more strongly toward the edge. At the moment when paraxial segment of the incident wavefront reaches mirror surface, its edge portion is reflected and converging toward the axis. However, while the paraxial mirror points (P) forms the wavefront section coinciding with the sphere SP, crossing the mirror vertex and centered at the paraxial (Gaussian) focus (G), the edge points form the wavefront section M, coinciding with a smaller sphere SM, centered at a point closer to the mirror, called marginal ray focus (CM). Other mirror segments form wavefront segments belonging to spheres centered at intermediate points in between these two (SI/CI). Phase difference at any of these points results from path length difference between the actual wavefront point and corresponding reference sphere point.

Coma aberration is wavefront deformation combining wavefront tilt with reduced wavefront curvature on one, and increased on the opposite wavefront side. Its origin is illustrated on a concave mirror (right), where points in phase on an incoming oblique wavefront above the chief ray (CR) point are progressively retarded relative to it, while those below are advanced, due to the optical path differences produced by tilt asymmetry (A'B' vs. AB). The effect is negligible only for a small central area of the wavefront, which belongs to Gaussian sphere (SG) and focuses at the Gaussian focus point G; the rest of wavefront focuses on points scattered above Gaussian focus. With the stop at the surface, mirror coma is independent of its conic, and increases with the angle of incidence.

Astigmatism is wavefront deformation where its radius of curvature varies from the minimum along one its diameter, to the maximum along diameter perpendicular to it. In a concave mirror with the stop at the surface, it is caused by an oblique wavefront section in the tangential (vertical) plane being of smaller diameter than in the sagittal plane (AC vs. BC, respectively, sketch to the right) - thus also focusing shorter (T vs. S, respectively). Also, central points are more delayed than the edge points in the sagittal plane (FE vs. DE), forming a deeper wavefront after reflection. Consequently, sagittal radius focuses shorter than the Gaussian sphere (SG, focus G), producing field curvature deviating from Petzval's in addition to the astigmatic focus distortion. Mirror astigmatism is also independent of the conic but, unlike coma, increases with the square of the angle of incidence.

The three point-image-quality primary aberrations are shown below in their physical manifestation, as intensity distribution disturbance within the point-source image in both, visual and graphical (point spread function) form, for a relatively large aberration level (0.15 wave RMS corresponds to 1/2 wave P-V of primary spherical aberration).

The two point-image-position aberrations, if significantly pronounced, can also affect image quality, by creating noticeable defocus error in either visual or photographic use (field curvature), or by deforming straight lines, and/or proper shapes in the observed image.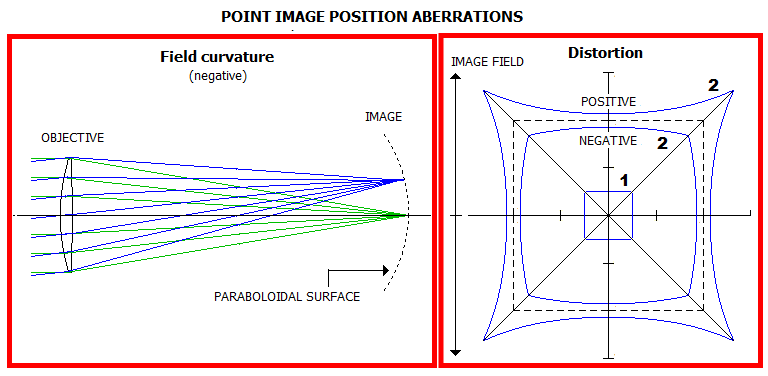

Properties of each aberration are described by the aberration function, based on a power series, with every successive power level - or "order" - resulting in significantly lower aberration contribution. First term of the series describes paraxial optics, but is too coarse to be used to define the aberrations. The second term is actually the first, or primary aberration term, the third term of the series is second aberration term, and so on. While higher-order aberrations can become significant in some optical systems, in most instances it is the second power term - so called primary, or Siedel aberrations - that practically determines the level of aberrations.

SECONDARY AND HIGHER ORDER ABERRATIONS

Higher- and lower-order aberrations are not separate entities; they are rather an artifact of the calculation method, aimed at simplifying extraction of the aberrations by using conic surface approximation. Thus, the relation describing depth of a conic (Eq. 4.1) is transformed into expansion series, with the surface sagitta (depth at the center) given by:

with d being the surface aperture radius, R the radius of curvature and K the conic constant (the first term describes parabola, with the conic -1, hence it's higher order terms equal zero). Lower- or 4th order (according to the exponent in d) wavefront aberration is calculated using the first two terms in the series; in fact, based not on the actual surface, but on its close approximation. It is sufficiently accurate for relatively weak and/or small in diameter surfaces, typical of most older-type telescopes, such are longer-focus Newtonians and doublets achromats.

With larger, more strongly curved surfaces, the next higher, 6th order term may become significant, in which case the lower-order aberration alone doesn't accurately present the amount - and the form - of aberration. In order to have a total of the aberration minimized, it has to be balanced with the higher-order form.

For instance, typically strongly curved lenses of an apo refractor induce relatively significant higher-order spherical aberration. If a system is constructed based on zero 4th order spherical aberration, the residual 6th order aberration is likely to compromise system performance. To prevent this, system surfaces are corrected as to allow for a certain amount of lower-order spherical aberration to offset its higher-order counterpart, so that the total aberration is minimized. Allowing certain amount of the lower-order aberration here is, in fact, correcting the actual surfaces beyond their 4th order zero-aberration approximation so that they are closer to that perfect surface profile that would produce a perfect wavefront.

Higher-order off-axis wavefront aberrations, coma and astigmatism, also result from this same conic surface approximation used in the aberration calculation. More complete coverage of the notation used for aberrations of different order is given at the beginning of Intrinsic aberrations section.

In a different concept, higher-order ray aberrations stem from the approximated incident angle on the surface, which determines the reflected or refracted ray angle. This concept dates back to the old days when raytracing was done by hand, using trigonometric functions. To simplify these calculations, it also uses an approximation from, this time, trigonometric function expansion series, such as sinα=a-(a3/3!)+(a5/5!)-(a7/7!)+..., with α being the incident angle on the surface in degrees, and a this angle in radians. For small angles (paraxial approximation, or first order optics) sinα is nearly identical to a; for larger angles, however, the difference becomes significant. Lower-order aberration calculation (Seidel) adds the second term, (a3/3!), which is why it is called third-order calculation. It is sufficiently accurate for weaker/smaller surfaces. Larger, more strongly curved surfaces may require adding the 5th order, or yet higher terms to the angle approximation in order to obtain sufficiently accurate result.

Higher-order terms in the conic sagitta expansion series - secondary or Schwarzschild, and more so tertiary and higher-order aberrations - are negligible with most amateur telescope types, and also significantly more complex. For those reasons, higher order aberration expressions are not given in this text. One exception is higher-order spherical aberration.

Follows brief overview of terms and conventions that are the basis of the aberration calculation.

◄ 3.3. Conics and aberrations ▐ 3.4. Terms and conventions ►

Home | Comments