7.1.1. CENTRAL OBSTRUCTION EFFECT: THEORETICAL INCONSISTENCY?

According to the theory, annular aperture has MTF cutoff frequency identical to that of a circular aperture of the same diameter. Since central obstruction (CO) results in smaller central maxima, the cutoff frequency (i.e. limiting MTF resolution) should be proportionally smaller.

The usual way of obtaining OTF/MTF is from the normalized exit pupil autocorrelation, where the integration area for the contrast transfer for aberration-free aperture is graphically presented as the overlap - normalized to the circle area - of two identical circles of the diameter equaling λfνc, where λ is the wavelength, f the focal length and νc the cutoff frequency. With νc=1/λF, F being the focal ratio, the center separation of these two circles at the cutoff frequency equals the circle (i.e. pupil) diameter. The same formalism is used to obtain OTF/MTF (for aberration-free aperture the phase OTF component is unity, and OTF reduces to MTF) of annular aperture, except that the overlap area excludes the area of central obstruction, and overlap is normalized to the annulus area (FIG. 104). Hence, the formalism results in the cutoff frequency for obstructed aperture independent of the size of obstruction, and equal to that of clear circular aperture, 1/λF.

While this formalism should accurately describe contrast transfer between zero and cutoff frequency for annular aperture, it is not appropriate for determining the cutoff frequency. The reason is that annular pupil produces diffraction pattern reduced in size with respect to that of clear aperture of the same diameter - in effect, a pattern nearly identical to one produced by a larger clear aperture with spherical aberration, in which the level of aberration does not cause change in cutoff frequency. In other words, it is physically impossible that a near-identical impulse response (PSF) produces two significantly different MTF cutoff frequencies.

This conclusion is consistent with the relation between PSF and OTF, which are for incoherent light Fourier pair, implying that any given PSF will produce a single corresponding OTF. Since the annular aperture PSF is narrower than that of a clear aperture of the same diameter, its OTF will be wider, i.e. will expand toward higher frequencies. Plots below illustrate the Fourier transform relationship between angular size of the PSF (first minima 1.22λ/D radians) and the extent of OTF frequency spectrum (linear cutoff period λF and frequency 1/λF, angular cutoff period λ/D period and angular cutoff frequency D/λ) for perfect circular pupil of diameter D (top) and for half as large perfect aperture (bottom) of identical focal ratio.

This is strictly valid for perfect unobstructed aperture, but as far as the cutoff frequency is concerned, it extends to apertures with significant level of aberrations (~0.5-1 wave P-V, depending on aberration type), as well as those with central obstruction in the usual range (up to ~D/2). Any change in the PSF shape changes the shape of OTF/MTF, which in this case represents a pulse, whose shape is determined by frequency spectrum represented by the PSF.
In general, reduction of transmission in the central pupil area increases the magnitude and/or size of (primarily) the 1st bright ring and reduces the central maxima radius, while reduction in the outer area suppresses the rings but increases the maxima radius. This makes the change in pupil transmission profile - in this case in the form of central obstruction - qualitatively different from aberrations. For simplicity, further consideration will be limited to aberration-free aperture.

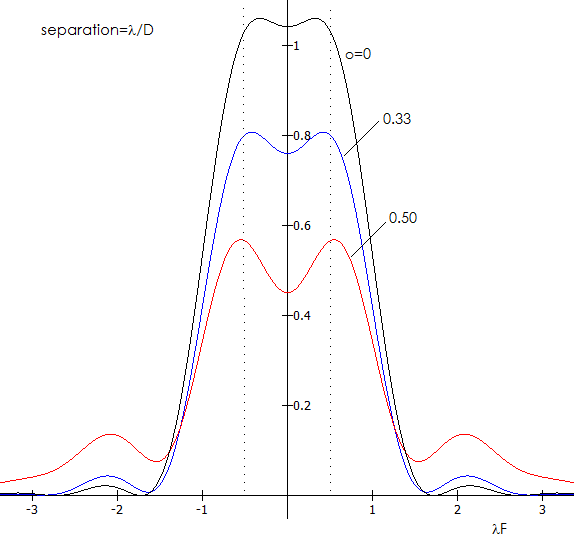
OTF is directly determined by the PSF and, while it uses a line pairs continuum, its cutoff frequency for aberration-free aperture is practically identical to that for a point source. Graph below shows what a pair of identical PSF functions, normalized to unit peak intensity, look like placed at λ/F separation, for clear, 0.33D and 0.50D obstructed aperture. Box at right shows those same plots for the more appropriate relative intensity distribution w/o vignetting effect (i.e. central intensity given by 1-o²).

At λ/D separation, perfect clear aperture has intensity deep between the two peaks of ~1.7%, for less than 0.9% contrast (from the general contrast relation, C=[I_max-I_min]/ [I_max+I_min], where the maximum intensity I_max is normalized to 1). At the same point separation, obstructed aperture not only has a deeper contrast drop in between two maximas, but also more widely separated peaks, the larger obstruction, the more so. It is obvious that the presence of obstruction should result in a higher cutoff frequency, and it is not necessarily in disaccord with a general statement that the cutoff frequency of an obstructed aperture equals λ/D. That same rule applies to apertures of all sizes, but they have different angular cutoffs, inversely proportional to the aperture diameter. It is evident that the presence of central obstruction, while not affecting focal length, hence neither the formal focal ratio, does shrink the physical diffraction pattern, without changing F-ratio, i.e. image scale. In other words, it makes diffraction pattern smaller angularly.
Assuming nearly identical resolution limit for two point sources (or lines), as for the MTF pattern, should be generally correct, considering it is valid for unobstructed aperture with significant level of spherical aberration (for instance, relative intensity of the first bright ring vs. central is nearly 40% higher with λ/2 P-V wavefront error of spherical aberration than with D/2 central obstruction, and the former still does not degrade the MTF resolution limit).

Taking a closer look shows that the ~1% contrast level of a perfect clear aperture at the point separation ~λ/D (i.e. λF linearly) corresponds to wider point separations for obstructed apertures than indicated by their actual central maxima width. For instance, at o=0.5 the central maxima radius is 19% smaller, but the 1% contrast falls not at 0.81λF, but at 0.88λF separation. By interpolating curve into the 1% contrast separation for the three obstruction sizes, an approximate rate of resolution limit with the increase in central obstruction can be obtained (right). Fair approximation of the resolution limit of an aperture D with the relative central obstruction "o" is given by (λ/D) (1-o³). Note that the 0.88 is rounded off; the exact 2% deep in the intensity, i.e. 1% contrast falls midway between 0.88 and 0.89. However, the 1.7% intensity deep, i.e. less than 0.9% contrast - equal to that of a perfect unobstructed aperture at λF separation - occurs at 0.88λF separation. Near threshold, it changes very quickly: at 0.9λF separation, intensity deep is already 4%, for 2% contrast, more than double that at the resolution limit.

The cause of the discrepancy between the smaller central maxima of obstructed aperture and its resolution limit is that for any given first minima radius, the FWHM (width at half-intensity) of obstructed aperture is wider, hence at any given radius value the sum of the two intensities is higher (below; for comparison purposes, both PSFs are normalized to 1). In other words, its central intensity profile is different than that of clear perfect aperture, resulting in a different corresponding OTF.

Follows an example of the obstructed aperture PSF and its properties, illustrating this conclusion, i.e. higher MTF cutoff frequency of annular aberration-free aperture vs. circular aperture of the same diameter. Raytrace was done with D=152mm f/5 mirror. At left, the base (obstructed) aperture diameter is 152mm, and the clear aberrated is 11% larger, corresponding to ~10% Airy disc diameter reduction with o=0.32. The latter has *lambda;/4 wave P-V of primary spherical aberration At right, the standard and proposed actual MTF plot for o=0.5 obstructed aperture.

LEFT: PSF of a clear aberration-free aperture of diameter D with 0.50D central obstruction (red) nearly coincides with the PSF of 19% larger (linearly, 1.19D diameter) clear aperture (blue, both for perfect and aberrated beaperture, as shown magnified in the box top right). For comparison purposes, all PSFs are normalized to 1. Central maxima of the obstructed aperture - reduced by about 19% in diameter due to the effect of central obstruction - is nearly identical to that of a larger aberrated clear aperture in monochromatic light (the latter is still slightly smaller, due to spherical aberration making the PSF maxima of the aberrated aperture slightly smaller than with the perfect aperture PSF). The two Airy discs radii are nearly identical, yet, according to the standard MTF formalism, the smaller obstructed aperture will have 19% lower cutoff frequency, given as D/λ (cycles per radian; related to the linear resolution as D/λf=1/λF lines per mm, f being the focal length and F the focal ratio), i.e. as much worse limiting MTF resolution. Evidently, there is no basis for such a difference in their respective PSFs.

MTF cutoff frequency does not change for primary spherical aberration up to 1/2 wave P-V, and somewhat larger, which implies that more energy outside the Airy disc shouldn't affect cutoff frequency for larger CO as well. Hence, the main determinant is the diameter of central maxima. Adding λ/2 wave P-V of primary spherical to the larger aperture causes the first minima to shrink somewhat - as a result of energy filling the gap - but the bell shaped curve, i.e. FWHM remains practically unchanged. Since it is the latter that actually determines the resolution limit, it remains unchanged.

RIGHT: the plots at right indicate that the actual effect of central obstruction on contrast over the range of MTF frequencies is significantly smaller than what the standard formalism implies. The effect of λ/4 wave P-V of primary spherical is (very) roughly comparable to that of o=0.5, not o=0.33 c. obstruction. Of course, two systems with different cutoff frequencies are not fully comparable; comparison is only possible over the range common to both of them, with the excess of resolution beyond that range being a qualitative advantage of the corresponding aperture in that respect. If this looks unrealistic, dwarfing the effect of central obstruction, think of all other factors involved. The typical instruments in comparison are a smaller refractor and larger reflector or catadioptric. For example, common belief is that a 6-inch reflector/catadioptric with ~D/3 c.obstruction compares to a 4-inch refractor (apo or long focus) with respect to planetary performance, and that it is central obstruction that causes it. But larger aperture has also larger seeing error, proportional to (D_l/D_s)^5/6. In this example, if the 4-inch aperture averages 0.075 wave RMS seeing error (comparable to λ/4 wave P-V of defocus), the 6-inch will average 0.105 wave (more than λ/3 wave). And the refractor typically also has smaller errors from miscollimation, thermal imbalances and surface imperfections.

In conclusion, I had a dialog with AI hoping it would give some information on this contradiction. It didn't. First it guessed it is because MTF is a pattern of continuous lines, as opposed to two lines, or point sources, where there is no energy overlap other than from the two sources, but couldn't explain why this does not affect cutoff frequency in the case of spherical aberration. Then it clung to the standard formalism of aperture size and the resulting size of point source diffraction pattern, but when confronted with a statement that the front end is irrelevant, what matters is the actual intensity distribution over the point image, it agreed.

◄ 7. OBSTRUCTION EFFECTS ▐ 7.1.2. Telescope central obstruction: size criteria ►

Home | Comments