5.2. Other air and atmosphere related errors

PAGE HIGHLIGHTS
• Low-level and local turbulence • Telescope tube currents • Atmospheric refraction and dispersion

In general, seeing error refers to the turbulence caused wavefront deformation in the atmosphere high enough not to be significantly influenced by thermal effects of the ground, and its configuration. Turbulence close to the ground has different forms and dynamics, usually referred to as local turbulence. Another level of turbulence is that caused by thermal imbalances in and around telescope itself, caused by uneven temperature of the telescope and its parts vs. surrounding air (heat from observer can also be significant factor). Finally, atmospheric layers around the Earth act as a weak lens, causing refraction, i.e. bending of light, known as atmospheric refraction, with its variation with the wavelength causing atmospheric dispersion.

Local turbulence

After clearing relatively thin layer of the atmosphere where the sideways movement of the upper level winds creates most of atmospheric turbulence causing "seeing error" in telescopes, light confronts more of potentially significantly non-uniform layers of air before it finally reaches the image plane. They are formed by local air currents at the observing site, movement of air inside closed telescope tubes and movement of air around thermally imbalanced optical elements, and other parts of the telescope.

Low-level turbulence results from terrain topography. For instance, valleys are filled with colder air during the night, resulting in greater thermal differential vs. ground and more intense low-level turbulence. Hillsides, including hilltops and bottoms, often have more unsteady air, due to constantly sinking cooler air. Strips along large water bodies have more unsteady air due to grounds and waters - and, consequently, air masses above them - being at different temperatures (one mini-version of such thermal air-clash is an open window). Low-vegetation and rocky terrain warms up more during the day, creating more low-level turbulence overnight.

In general, when high-level (atmospheric) turbulence is significant, it is the dominant component of seeing error. When, or where it is relatively insignificant, the low-level turbulence may become the primary seeing error source.

Local air turbulence is produced as objects and surfaces warmer than air - pavement, roofs, roads - raise the temperature of the air layer surrounding them, causing it to rise up forming turbulent, non-uniform light-transmitting structures. These layers of unsteady air can induce as much of optical error as atmospheric turbulence, or more. One local thermal offender not to be left out is the very observer, particularly with Newtonian-type telescope, when body warmth can directly affect both steadiness of the air in front of a telescope, and inside the tube, or open structure.

FIGURE 88:
Graph at left (top) shows measured temperatures of several surface types vs. air temperature at four locations in the Northern U.S. For telescope users, of primary interest are hours between twilight and dawn (shaded columns).

Measured temperatures show little difference between foliage and air, but grass surfaces remain warmer than air, with the difference increasing from 2-3°C at sunset, to several degrees before dawn. Bare soil is significantly warmer than grass at sunset, but after a few hours remains only moderately warmer.

As expected, asphalt, concrete and roofs are surfaces with the highest thermal differential vs. air. It is particularly pronounced at sunset, but even deep into night time these surfaces can be as much as 10°C, or even more, warmer than the air.

The type of weather - sunny, cloudy, or rain - influences the thermal differential. Higher night time air temperatures indicate cloudy weather, possibly some rain, reducing thermal differential of all surfaces vs. air. The greater thermal differential of surfaces beneath the air layer and air above, the more heat transferred to the air, and the more intense ensuing air turbulence.

As shown at left, ground turbulence is initiated by heat transfer via conduction (i.e. molecular friction) between the surface and the air layer next to it. Pockets of less dense, lighter warmed up air lift up, creating raising plum structure. The speed at which it moves upward is determined by temperature differential vs. cooler surrounding air. As the plums move upward, they spread wider and cool down, which in turn slows down their movement. As the thermal differential vanishes, so does the turbulent structure: the plums dissipate into surrounding air.

Specific height above the surface at which turbulence reaches maximum, as well as the height at which it practically vanishes, depend mainly on the magnitude of surface-to-air thermal differential. Ground turbulence shown should be within the average range; it is worst at about 0.5m height, still nearly as strong at about 1m, and subsiding significantly at about 2m and above. This is one factor that works for large, long focus refractors, whose entrance pupil is above the level where this kind of turbulence can be significant.

Telescope tube currents

The threat of unsteady air continues inside the telescope tube. If the tube is warmer than the air - the usual scenario - it warms up the air causing natural movement of warmer air upward, and colder air downward - creating tube currents. This results in a constant steady flow of air inside telescope tubes - the more out of thermal balance with the air, the more so - creating areas of varying air densities within the tube. The effect is more pronounced in long, open tubes, due to constant influx of (usually) cooler air from outside the tube, than in closed tubes. It is also generally more pronounced in tubes pointing to lower altitudes.

Compared to atmospheric turbulence, thermal imbalances between surrounding air and telescope tube tend to produce more uniform stream of warmer air. But its uneven optical density causes light to propagate at different speeds, deforming the wavefront and diffraction pattern it produces. Typical tube current is a slow flow of warmer, lighter air from the bottom toward the upper part of the tube, where it forms the layer of slightly lower optical density. Light moves through it at a higher speed, advancing that wavefront portion with respect to the portion moving through slightly cooler air below.

Since 1°C thermal differential changes air refractive index - and the speed of light in it - by approximately 0.00011%, a 1,000mm long tube with that much wormer air in the top of the tube would generate 0.0011mm wavefront deformation - 2 waves P-V in units of 0.00055mm wavelength (since relatively small part of the wavefront is affected, the corresponding RMS error is significantly smaller - roughly 2 to 3 times, or ~P-V/10 - than with aberrations affecting the entire wavefront).

The last layer of unsteady air waits at the very optical surface. Thermal imbalance between the air and optical elements it surrounds creates thin layer of turbulent air in front of their surfaces (FIG. 89). Even small thermal imbalances of this kind can induce significant wavefront deformations. This effect is also influenced by the aperture size and thermal efficiency of the mechanical design. Natural (passive) thermal balancing often works well enough to diminish this source of error. However, large apertures and/or thermally closed or in some other way inefficient systems will likely require assistance of fans. Brian Greer's investigation gives more detailed insight into thermally induced errors in a Newtonian; Alan Adler's article addresses management of thermal currents arising from mirror surface.

FIGURE 89: Illustration of the effect of tube and off-surface air currents on the flat incident wavefront W (exaggerated). LEFT: Open tubes are more prone to currents due to a constant feed of cooler (than the tube) air, sliding along the tube bottom and moving upward as it warms up. This creates air layer of lower optical density toward the tube top. As a result, portion of the wavefront moving through it advances with respect to the rest of the wavefront. RIGHT: Similarly, optical element warmer than surrounding air will transfer thermal energy to it, initially by conduction, and then by convection, i.e. physical movement of warmer air molecules upward. This creates stream of air pockets of different optical densities in front of optical surface, deforming passing-through wavefronts.

The extent of air disturbance caused by a thermally deformed optical element is roughly proportional to its diameter and thermal differential. Assuming arbitrarily that the spatial extent of turbulent air at the optical surface is D/3, D being the element diameter, and average temperature differential of relatively large pockets of warmer air about 2/3 of the temperature differential between the element and surrounding air ΔT (considering that warmer air concentrates in relatively small areas toward mirror top portion) possible maximum P-V wavefront deformation caused by it would be given by DΔTι/4, with ι being the change in refractive index in the warmer pocket vs. surrounding air.

With the refractive index changing by ~1.1x10-6 (0.0000011) for 1°C change in temperature, the maximum wavefront deviation would be P-V~2.7Dx10-7 for every 1°C differential between optical element and the air. That gives ~1/20 wave P-V (550nm wavelength unit) per 1°C of thermal differential for D=100mm, and ~1/4 wave for D=500mm.

Obviously, these results are only as good as the assumptions made. Again, similarly to the tube current wavefront deformation, these peaks typically affect relatively small wavefront area, so that the overall error is significantly smaller than with identical nominal P-V error of classical aberrations. Very roughly, the corresponding RMS wavefront error could be approximated by P-V/10; that would make optical damage to image quality caused by 1 wave P-V of the off-surface thermally induced aberration roughly comparable to 1/3 wave P-V of spherical aberration.

Note that the effects of off-surface thermal currents and tube currents will combine into a larger final magnitude of wavefront deformation. Both are affecting most the portion of the wavefront in the upper part of the tube in a roughly similar manner, by causing its relative advance (the roughness component is significantly greater - likely dominant - in wavefront deformation caused by off-surface currents, compared to wavefront deformation caused by tube currents). Whenever there is thermal imbalance between telescope and surrounding air, the third component of thermally induced error - optical surface deformation - will also be present.

Very approximately, by doubling the above wavefront error caused by off-surface currents (telescope tube is much longer than D/3, but also cools much more quickly), the combined error resulting from thermal imbalance can be placed at ~D(mm)/10,000 wave RMS (in units of the wavelength) for every 1°C difference in temperature. That corresponds to ~0.01 wave RMS per every 100mm of aperture, per 1°C. Since the glass-to-air thermal differential in thermally inert systems can remain at up to several degrees for hours, the potential error is significant: it can be over 0.05 wave RMS in 100mm aperture and over 0.2 wave RMS in a 500mm telescope. Of course, it can vary significantly from one telescope to another, depending on its mechanical (forms, thickness) and thermal properties.

The length of cool-down of an optical element in air is nearly proportional to its volume. Given its thermal emissivity coefficient, the greater volume, the longer it takes to achieve thermal near-equilibrium. Since the rate of conduction is proportional to the surface area, and thermal capacity to the glass volume, a 24-inch mirror will require many times longer to reach thermal near-equilibrium as a 6-inch of the same glass and relative thickness. With 6-inch mirror in a properly built cell requiring up to 2 hours for near-complete cool-down, large reflectors may not settle thermally for the entire night.

Given telescope-to-air thermal differential, the degree of thermally induced wavefront deformation arising from uneven air temperature in and around telescope depends on its mechanical design, material thermal properties and size. In general, larger apertures are affected more. Also, it is less noticeable in refracting telescopes, due to their design and smaller apertures. At near-steady air temperature, the effect generally diminishes as a result of passive thermal balancing, but may persist if the initial tube-to-air differential is large, and/or if the air temperature keeps changing, especially with larger telescopes and thermally unsound mechanical designs.

Unlike atmospheric turbulence, this source of error can be greatly reduced with proper mechanical design and use of fans.

Other telescope parts - cells (special attention needs to be paid to avoid thermally inert primary mirror cell in reflectors), holders, diaphragms, miscellaneous mechanical parts - can also be out of thermal balance to the degree causing noticeable wavefront deformations. Finally, thermal effects caused by observer's body, either by direct contact with a telescope, or by air disturbance resulting from body's warmth, can cause noticeable image deterioration. As already mentioned, the latter is particularly of concern with Newtonian-type telescopes, with the eyepiece located relatively close to the path of incoming light.

Quality observing with medium to large aperture telescopes requires all significant sources of thermally induced errors eliminated or minimized.

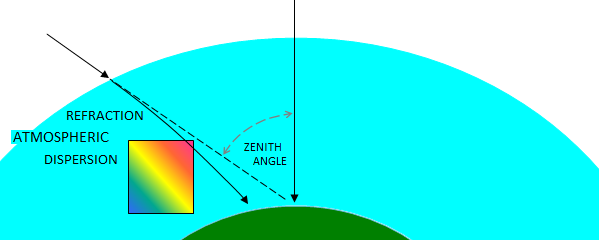
Atmospheric refraction and dispersion

Light entering Earth's atmosphere from space travels through an increasingly denser medium, from the refracting index n=1 for vacuum to n'=1.00029 (for 550nm wavelength) near ground, thus it gradually bends away from its previous path, and toward ground, i.e. refracts.

Even if this change of path direction is very small, its effect may not be negligible with respect to the aberration induced - lateral color error, caused by the angle of refraction varying with the wavelength (dispersion of light). Both, atmospheric refraction and dispersion are zero for zero zenith angle (left), and increase as a function of its increase. Refraction angle in radians is given by A=tanZ(n'-1), in radians, where Z is the zenith angle and n'-n is the index change. For Z=45° and 0.00029 index change for the green light, it gives 0.00029 radians, or 1 arc minute (from 0.00029 x 57.3 degrees in a radian x 60 arc minutes in a degree).

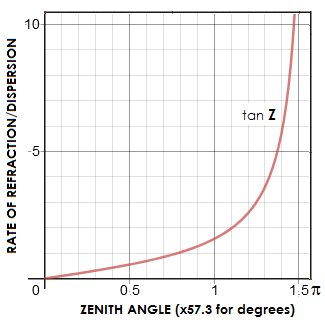
Both, angle of refraction and dispersion change with the tangens of the zenith angle, as shown at left. The change is exponential, with either being about five times larger at Z=78°, and already ten times larger at Z=84°, than at Z=45°.

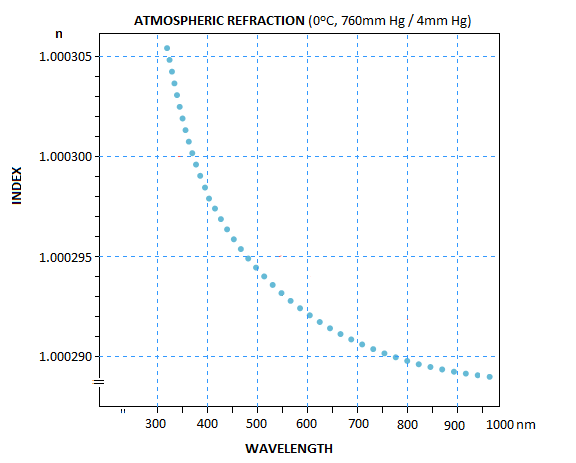
With shorter wavelength having greater index change than the longer ones, atmospheric refraction results in dispersion of light, with the white incident light splitting into a rainbow. The width of this color spread is determined by the index differential between the wavelengths, as L=-tanZ(Δn'), also in radians, Δn' being the index differential (marked as Δn on the graph). It is shown on the graph below, for 0°C temperature (based on data quoted in "Astronomical optics", D. Schroeder). In warmer air, the entire plot shifts by about 0.000015 in index value lower, but the change in index differential is relatively small; at 15°C, Δn' for the range shown is about 10% smaller, and less than that much at 30°C vs. 15°C. By far the largest factor is the zenith angle.

Taking again Z=45° and about Δn'=0.0000055 index differential between the F and C lines, gives 1.13 arc seconds (from 0.0000055 multiplied by 206,265). Obviously, in terms of lateral color error, larger apertures with smaller Airy discs will be affected more than smaller apertures. Here, F-to-C separation of 1/2 Airy disc diameter, at which the photopic polychromatic Strehl drops to 0.80, corresponds to the Airy disc diameter of 2.26 arc seconds (for 550nm wavelength), i.e. to a little over 120mm objective diameter.

As the diffraction simulations show (bottom), this level of atmospheric dispersion is not intrusive (simulations are for a bright telescopic star and very high magnification). However, in the twice larger aperture (top), it is significantly more noticeable and degrading (note that the diffraction image is not scaled to the Airy disc, and that diffraction images for the two aperture sizes are given on the same scale). On the bright extended objects it will produce bluish and reddish fringing on the opposite sides, in the plane of atmospheric refraction (all simulations are shown for upright image; most telescopes will show it turned upside down). Simulations for several wavelengths in the 400-830nm range show that - as the index differential graph indicates - lateral color error due to atmospheric dispersion increases much faster toward the violent end, than toward deep red.

◄ 5.1.2. Seeing error: Strehl, resolution, OTF ▐ 5.3. Misalignment and forced surface errors ►

Home | Comments