telescopeѲptics.net   ▪   ▪   ▪  ▪ ▪▪▪▪ ▪ ▪  ▪   ▪    ▪     ▪      ▪       ▪        ▪         CONTENTS
 

Another factor of glass homogeneity is the amount of bubbles and inclusions (generally all particulate contaminants) it contains. While leading manufacturers claim that both are reduced to negligible in their standard glasses already - which the specified tolerances do confirm - it is certainly possible that less than acceptable glass in this respect finds its way into telescope optics. The effect is primarily light scatter, most likely low in magnitude, so it may not be easy to track down.

4.9.2. OPTICAL COATINGS

A bare glass surface, whether for mirror or lens, is rarely a finished product: it is treated with coatings. Optical coatings are thin layers of metal deposited on optical surface in order to enhance its optical properties. Reflective coatings greatly enhance reflectivity of mirrors, to the extent that they are practically a must. Anti-reflective coatings, applied to a lens surface to minimize transmission losses and/or internal reflections much less enhance performance level, but it still can be significant, particularly in the systems with numerous lens surfaces. The main factor affecting wavefront integrity - possibly significantly - is in either case the variation in layer thickness.

Reflective coatings

Figure-scale wavefront deformations cause relatively narrow energy spread, similar to that of common aberrations, only smaller in magnitude. Small-to-microscopic local wavefront deviations - wavefront roughness - and obstructions to wave propagation cause wider energy spread - the smaller they are, the wider - but the amount of energy they move is generally smaller. Follows more detailed examination of the possible magnitude of coating-induced errors.

Figure-scale wavefront deformation due to non-uniform film thickness profile

 The thickness variations are, in general: (1) smooth radial, from center to edge, and (2) random local, the former being the gradual decrease in thickness toward the edge (typically), due to the the angle-of-emission-dependent change in density of the coating material depositing onto substrate, and the latter due to random small-scale non-uniformities in the material flux density. In the context of non-uniformity of optical surface, they relate similarly as figure vs. random local errors, only with generally smaller magnitude.

Radial decrease in layer thickness toward the edge, due to the decrease in the rate of deposition for substrate points farther off the material source center. As illustrated at left, film deposition rate for point-source depend on the 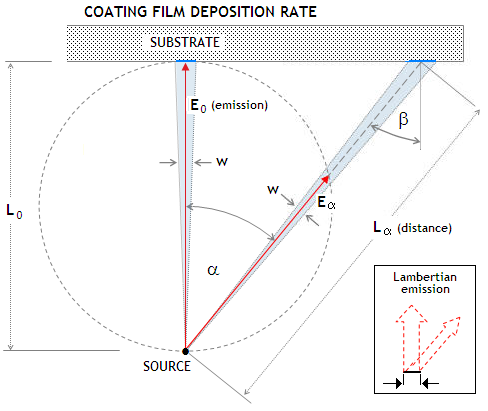direction of emission (α), substrate distance (L), and substrate angle (β). The first factor makes material emission rate proportional to cosα (Lambertian emission, illustrated graphically in inset bottom right), the second to cos2α, and the third, determining the area of deposition on the substrate, proportional to yet another cosine factor. In all, in the schematic shown, with the substrate oriented perpendicularly to the axis of emission (i.e. α=β), deposition rate changes in proportion to cos4α. By manipulating substrate angle and/or position (e.g. by some form of a planetary rotation over source), and the effective emission rate to specific substrate areas by use of a mask, the falloff in deposition rate toward substrate edge can be significantly reduced. In practice, the rate is typically between cos2α and cos4α, depending on the substrate size and required surface accuracy.

Film deposition rate as a function of the emission angle for parallel plane substrate and point-source evaporant can be graphically presented as cosnα, n being the cosine exponent for the effective deposition rate specific to coating process, either in Cartesian or polar coordinates (assuming, for simplicity, that emission and deposition rate are nearly proportional, which may and may not be the case in practice). As shown below, the former gives better indication of film thickness falloff, while the latter gives graphic indication of the directional intensity of point-source emission. When n=0, deposition rate is constant and independent of the emission angle; it is Lambertian for n=1 and bell-shaped (Gaussian) for the usual range of n values, 2≤n≤4. Deposition rate at 30° emission angle falls by 25% for n=2, and by 44% for n=4, hence the angle has to be significantly smaller for optical coatings. One way to reduce the effective emission angle farther off source axis is to expand emission (source) area.

This is a general model of emission and deposition for a point like evaporant. Usually the evaporant has some form of extended surface, and/or multiple sources are present. This correspondingly extends the area of near-even emission/deposition rate, but the emission and deposition rates at oblique angles decrease at a similar rate (for extended source somewhat faster relative to the emission and deposition rates above the source).

This general modeling of emission and deposition rates with thermal evaporation, where the emission is produced by raising source temperature, is also applicable to other coating methods, such as sputtering, where material emission is produced by targeting the coating material source with a beam of accelerated (in electric or magnetic field) ions. In either case a cloud of coating material spreads out and sets onto substrate in a similar manner.

These are only the basic consideration, used for determining film deposition equation in every specific case. It is the starting point, but the actual deposition is optimized empirically. Specific values for the radial film thickness error for given coating apparatus depend on the substrate size and possibly other factors, such as curvature of substrate surface and its sign. Looking at the film deposition rate (top), a point-source evaporant (in practical terms a source much smaller than the substrate), with film deposition rate proportional to cos4α, would need about 11° radial angle, or so, in order not to exceed 10% edge thickness fall-off. For 400mm diameter mirror, that would require source-to-substrate distance of nearly 1m, which would require very large coating chamber (roughly twice as large), and would be also more wasteful of evaporant. Half as large distance is more realistic, but it doubles the angle of emission at the edge, resulting in about 25% thinner film. What is the error to the wavefront? Graph below illustrates the resulting surface and wavefront deviation, as well as the final wavefront error, greatly magnified vertically.

At the film deposition rate proportional to cos4α, the edge emission angle for 25% thickness drop-off is 21.47°. Assuming perfect surface and 0.3 micron film thickness in the center, the edge will be 0.075 micron thinner, doubling in the wavefront to 0.15 micron P-V wavefront error. Since the form of wavefront deviation is very similar to that of compensatory defocus (shown of the same sign as the film-induced error, for comparison), most of the error can be cancelled out by refocusing. The resulting P-V wavefront deformation, shown on top (magnified by a factor of 2, for clarity) is identical to the best focus primary spherical aberration. It measures 0.0147 (i.e. 1.47% in terms of the center film thickness), or smaller than the maximum film thickness deviation by a factor of 17 (and twice smaller from the resulting P-V wavefront deviation), in this case 1/125 wave in units of 0.55μm wavelength.

With the film thickness drop-off proportional to cos2α, the edge emission angle for 25% thinner film at the edge is somewhat larger, 30° (which, all else equal, would allow coating of nearly 50% larger substrate). Here, the maximum difference between resulting wavefront deviation and defocus is somewhat smaller, 0.0113 (i.e. 1.13%), and so is the final wavefront error: 1/163 wave P-V.

So, as long as the radial film thickness changes approximately with cosnα, even with fall-off as quick as with n=4 and 25% center-to-edge difference, the resulting wavefront error - primary spherical aberration - is entirely negligible. However, life gets more complicated, and one of the reasons is that 25% - or, for that matter, 15% - film thickness non-uniformity may not translate into a strong selling point. But in the process of reducing this nominal non-uniformity to, say, more appealing 10%, ±5%, or ±2%, coater might replace this steady exponential change in the radial film thickness into unsteady one. For instance, multiple point sources may be introduced, source area may be expanded to relatively significant vs. substrate, and or shadowing mask may be used (if point sources, or source area, are extended linearly, with rotating substrate). The resulting surface/wavefront deformation may be significantly less offset by refocusing than the steady cosnα deviation.

Taking the same 400mm diameter mirror, in order to make it comparable, first example is the coating profile resulting from continuous circular source area about half the diameter of the substrate (top left). Film thickness is uniform up to about half mirror radius, and then diminishes to the edge in proportion to cos5α (at somewhat faster rate due to extended source), with the edge angle being twice smaller than with point-source. This results in the maximum thickness deviation at the edge of little over 6% (a). it doubles in the wavefront, generating deformation similar to turned-down edge beginning at 50% zone (b). This wide zonal error toward the edge still can be reduced by refocusing, with the approximate minimum error achieved by bringing to zero edge deviation. Hence the needed defocus is identical in the P-V error, and of opposite sign to the error generated by non-uniform coating (c). However, the resulting final error (d) much less reduced than with steady cosnα film thickness deviation, and rather peculiar in its form. The error peaks at half the radius, forming an angle there. Very roughly, it can be compared with about 20% smaller P-V error of primary spherical aberration at best focus (dashed). That would put it at 0.025 (i.e. 2.5%), smaller than the maximum film deviation by a factor of 2.5, or 1/5 of the P-V wavefront deviation it caused.

In other words, while its nominal film thickness error is more than four times smaller than with a point-source and 25% edge thickness drop-off, the final wavefront error for this film thickness profile is larger by a factor of 1.7. With the same film center thickness of 0.3μm, that comes to 0.0075μm, or 1/74 wave P-V in units of 0.55μm wavelength.

Other film thickness profiles are also possible. A deviation split into near equal positive and negative with respect to the center thickness, it may may look like radial profile shown on bottom graph. Here, ±3% deviation similar in its nominal magnitude to the one above, doubles in the wavefront as shown, and can be partly minimized by refocusing to 0.075 (i.e. equaling 7.5% of the film center thickness) final P-V wavefront error, three times larger than for profile above. This wavefront error also peaks at half the radius, but in a form of an arc. Its RMS wavefront error is 0.258 its P-V, which implies it is comparable to about 15% smaller P-V error of primary spherical. For 7.5% of 0.3μm and λ=0.55, that comes to λ/28 wave P-V of spherical aberration (the effect is somewhat different, with this aberration form mainly brightening the dark rings - particularly the second, fourth, etc. - while having little effect on the bright rings, except the second one, which becomes brighter). This becomes marginally significant, because it would add to primary spherical of the same sign nearly arithmetically (lessened approximately by those same 15%) so, for instance, would cause a λ/6 P-V mirror to become effectively λ/5.

And if the radial coating thickness profile would have such arc form to begin with, it would simply double in the wavefront, with no possibility to reduce the error by refocusing. If the maximum thickness deviation here is also 6%, the final P-V wavefront error would have been 12% of the center thickness, or 0.036μm for 0.3μm thickness: λ/15.3 wave P-V with 0.55μm wavelength, comparable to λ/17.6 wave P-V of primary spherical. It would make a λ/6 mirror effectively λ/4.5 (on the other hand, if their respective signs are opposite, it would have it bettered to λ/9.1).

These few examples illustrate: (1) that wavefront deformation induced by the radial film thickness error with reflective coating is much more dependant on the type of radial film profile, than on its nominal thickness non-uniformity, and (2) that can be considered generally negligibly small, but that it is possible for it to be contributing more than negligible amount of deformation to the existing aberrations.

All of the above refers to the bare - so called unprotected - reflecting coating. Having protective coating applied over the basic mirror coating is quite common these days, and it can cause additional wavefront deformation. Its thickness is comparable to that of the basic coating, but the error induced to the wavefront, for given thickness deviation, is smaller, due to it being transmitting (i.e. the wavefront error is generated due to the differences in light speed in two mediums, like at the lens surface). However, the error at the top surface of the protective layer combines with the error at the surface of the reflective coating. Light passes the front surface twice, on the way in and out, thus the P-V wavefront error resulting from thickness deviation v at the front (air-to-protective coating) surface is 2(n-1)v, with n being the refractive index of the protective coating. For the rear surface of the protective coating, wavefront deformation is caused by the variation in thickness v' of the protected reflective coating, with the P-V wavefront error given as nv'.

Similarly to reflective coating, wavefront deformations here can be caused by large, figure-scale film thickness non-uniformities, small random ones, and by the film surface roughness. The latter two are addressed in the roughness section below. As for figure-scale errors induced by the protective coating, its effect, as with reflective coating, will depend more on the radial film profile form, than the nominal error itself. If we assume film profile form similar to that of the reflective coating, it will partly compensate for the reflective coating error by delaying light less - in effect advancing it - in the thinner portions of the profile.

For the film thickness differential ∆t, the P-V wavefront error induced by the protective layer is n∆t-1. For film thickness decreasing toward the edge with cosnα, assuming similar layer thickness for both films, the combined error is 2∆t-(n∆t-1)=(2-n)∆t+1, or smaller by a factor of 1-[(n∆t-1)/2∆t]. For n=1.4 and ∆t normalized to unit, error reduction is 20%. Since the error from this profile type is negligible, such reduction has no importance, and even in the case when film radial non-uniformity adds to spherical aberration of the surface, the effect is rather small.

Instead of a single reflective coating, protected or not, mirror can use multiple layers of alternating high and low index materials. It is called dielectric mirror, and works on the principle that every next layer collects some of the light missed by the previous layer, with layer thicknesses and indici ensuring that all reflected light comes out in phase. Hence more layers generally mean higher reflectivity; enhanced 96-97% requires up to several layers, and 99%+ up to a dozen, or so. Since every layer is about quarter wave thick (that may vary somewhat with the preferred reflectance curve), dielectric reflective coating can be up to a few waves thick. Since the combined error increases with the number of layers, dielectric coatings require higher single layer thickness uniformity in order to achieve given minimum wavefront distortion. This applies to both, random small-scale thickness variations and radial thickness error.

For instance, a 10-layer high-reflective coating with 2.5 waves center thickness and consistent 5% thickness figure error, would generate 1/8 wave P-V differential, doubling in the wavefront to 1/4 wave. Again, the consequences with respect to the final wavefront error are mainly determined by the type of profile. But in general, the maximum error for an individual layer here should be roughly as many times smaller than for a single layer as many reflective layers there are.

The effect of the coating surface roughness

Local random thickness deviations over the surface can be assumed to be less than 2% (± 1%). With 0.3 micron (μm) thick coating, this surface error doubled in the wavefront would be less than 0.006 microns (6nm), or roughly 1/100 wave P-V for 550nm wavelength. With the worst-case P-V to RMS ratio of about 3, and a pattern of varying thickness over entire surface, this surface roughness would cause less 1/300 wave RMS wavefront error, or 0.05% energy scattered in a vide radius around the Airy disc (similarly to micro-ripple, the radius of scatter vs. Airy disc is radius well approximated by a ratio of the average diameter of such deviation vs. aperture diameter). While this type of error cannot be reduced by refocusing, it is small enough to be negligible alone. Picture below illustrates this type of film thickness error within its usual magnitude range (note that the radial film

thickness error is also present). These local irregularities result from variations in the deposition rate over substrate, starting with the initial islands of coating material on substrate surface over which newly arrived atoms spread and grow. It is also related to the grainy structure of the film - grain being a conglomerate of smaller crystals, themselves related to the columnar film growth - where grain sizes, depending on the specs of deposition process, usually range from 5nm to 25nm in their surface diameter. Their height on the surface, however, is only a small fraction of it.

With protected reflecting coating, random local small-scale errors, assuming uncorrelated thickness deviations for these two layers (which is not strictly correct, since any unevenness of underlying layer would to some extent "imprint" its shape into inherent unevenness of the top layer), and similar magnitude of local deviations at the first and second surface of the protective coating (v~v', respectively), the combined error is a square root of the sum of each of them squared, or [n2+4(n-1)2]1/2v. For n=1.4, the thickness variation would be enlarged in the wavefront by a factor 1.6. With v and v' on the order of 1/300 wave RMS, or less, the effect is still negligible.

Taking as the maximum acceptable small-scale roughness P-V wavefront error of less than 0.03 (±0.015) microns (~1/20 wave in units of 550nm wavelength, for 0.99 Strehl degradation factor) would require the random film thickness variation v of the two layers to be no more than 0.015/2[n2+(n-1)2]1/2 microns. For n=1.4 the denominator is 2.9, and deviation would have to be less than 0.015/2.9=0.005 microns (5nm), or ±0.8% for 0.3μm coating. In other words, light scattered due to random local film thickness variations with properly applied coating, bare or protected, should remain below 1%. With an actual coating it is likely to be a small fraction of it.

Standard reflective coatings should have RMS surface roughness below 10nm and, when quoted, it is usually below 5nm; typically in the 1-3nm range. That would double in the wavefront to nearly 1/100 wave RMS, for less than 0.4% energy loss (scatter). However, the actual scatter measurements commonly indicate 2-3 times larger coating roughness, as RMS surface error, than what this nominal figures - usually obtained by profilometers at the place of fabrication - indicate. While background scatter is consistent with the roughness figure, there are random large local peaks (that may escape roughness measurement over small areas) scattering more light than the rest of surface. These defects seem to be inherent to the film, hence generated by the coating process. If corrected for this factor, the wavefront roughness due to reflective coatings could be up to three times, or so, larger, in which case it would scatter over 4% of light energy.

These random scatter peaks in the coating could be in part related to the high absorption spots formed by low- and non-reflective impurities, acting as inverse micro apertures transferring energy out of the central diffraction maxima at wide angles.

As above illustration indicates, coating roughness has two different scales: one, larger, created by local deviations in film thickness, and the other, which we can call microroughness, the result of inevitably less than perfectly smooth surface of crystallized atoms, to the smaller or larger degree also affected by the porous film structure. These two appear to be, at least roughly, of similar magnitude, up to about 1% film thickness. Since unrelated, they add up as a square root of their respective squared magnitudes. Taking as the worst case scenario ±1% of the film thickness deviation, with 0.3 micron film thickness, for both, gives 6nm P-V error doubled in the wavefront to 12nm for either one. Assuming P-V to RMS ratio 1:3 it is 4nm RMS for each. In units of 550nm wavelength it comes to (0.0072+0.0072)0.5, or 0.01 wave RMS, resulting in 0.4% energy scatter.

 Coating roughness produces effect similar to substrate (glass) small-scale and micro-roughness. Considering that reflective mirror coatings are generally thin (0.1-0.3μm), the two roughness forms combine resulting in a roughness scale larger than either of the two alone. While mid and small-scale substrate roughness occasionally can be atypically large, microroughness usually does not exceed 1-2nm, i.e. it is roughly comparable to the typical coating film microroughness. In other words, reflecting optics made with standard procedures shouldn't be scattering more than 1% of the light falling on it (mid and large scale roughness do not widely scatter light, they move energy to the rings area).

The effect of non-uniform film reflection

As stated in the beginning, in addition to wavefront errors induced by a reflective coating, optical quality is also affected by the change in the pupil transmission map due to imperfect consistency of the reflective layer. Of main concern are microscopic holes, cracks and semi-reflective or non-reflective specks. They act as microscopic inverse apertures, effectively light obstructions, transferring energy from the central maxima out, over extremely wide radius. Picture at left shows typical grainy surface structure of aluminum film, greatly magnified (it is about 0.02 by 0.02mm). Due to photographic effects, these photographs may not accurately represent the actual reflectivity map, but do indicate areas of uneven reflectivity. Low-reflectivity spots are either impurities, or light traps in the porous film structure. Partial reflectivity spots have basically the same type of effect, only in the proportionally smaller magnitude. For instance, a 50% reflectance spot will throw about half as much energy out at wide angles as a near-zero reflectance spot. Little attention is paid to this aspect of coating quality, and that is why it may be underrated as a problem. 

The amount of energy scattered is proportional to their relative transmitting pupil area squared (it is so in the standard theoretical approach, which assumes near monochromatic point source, i.e. coherent light; the actual light from astronomical objects is typically polychromatic, i.e. partly incoherent, and the effect is significantly smaller).

For instance, if these microscopic obstructions effectively cover 0.5% of mirror surface, it will reduce the central energy in coherent light by a 0.9952=0.99, with 0.01 (1%) of the energy spread over a wide radius (approximately, the radius is greater than the Airy discs' by the ratio of mirror diameter vs. average diameter of the coating hole). With incoherent light, only half as much.

Assuming 1% energy loss per reflecting surface as the maximum acceptable, such non-transmitting area combined - again with coherent light - shouldn't exceed 5,000 square microns per mm2 of the coating, i.e. shouldn't be larger than 0.07x0.07mm square in it. However, since small-scale surface variations in the coating thickness, as well as dirt/dust surface contamination need also be included, the actual tolerance is tighter. Just for illustration, assuming that each of the three contributes similar amount of scattered light, the individual tolerance for each would have been 0.33% scattered energy. It translates into no more than 0.167% of mirror surface covered by non-reflecting specks in the coating, or 0.04x0.04mm per mm2.

Such data, however, is not provided, neither with telescopes, nor by those directly doing coating services, and we, again, can only speculate what is the real figure.

In general, it is fair to assume that properly applied, fresh coatings do satisfy these minimum requirements. However, decay due to exposure and damage to the coatings in its use, could significantly worsen quality of a reflective coating, resulting in unacceptable amount of scattered light. This seems to be supported by measurements taken at this professional observatory.

They indicate that reflective coatings can deteriorate significantly in a relatively short amount of time, with their reflectance remaining relatively unaffected (of course, it cannot be ruled out that similar sub par performance could result from improper application as well). While we don't know how representative they are of the typical commercial coating, what they imply is that dust/dirt are the dominant - and significant - factor of scatter from mirror surface in a relatively short period of time (one year, or so) in between two successive removals, with the combined scatter reaching 5%, or more, per surface. But scatter due to the coating itself may have high relative rate of increase with time, and could become dominant with a coating that is several years old. Significant part of coating deterioration may be related to an increase in the total area of low- and non-reflecting spots.

Adding to this the detected discrepancy between the nominal coating roughness figures obtained by measurements, and the actual measured scatter, noted above, helps explain, at least in part, anecdotal evidence of generally darker background in refracting vs. reflecting telescopes.
 

Transmitting coatings

In comparison, lens coatings seem to be significantly more durable and, for given application quality, having significantly less of an impact on the optical quality. These antireflection coatings can have a number of layers varying from one to a dozen, or more. Their purpose is to enhance transmission by reducing or minimizing reflections off glass surface, and even more to minimize stray light resulting from these reflections. Since these coatings are transmitting, not reflecting, they generate less of a wavefront error and have, in general, significantly more relaxed tolerances than reflective coating. For a given number of layers and layer non-uniformity, the wavefront error induced by them is roughly 2-4 times smaller. In other words, these coatings will satisfy the minimum error requirement with significantly more relaxed layer accuracy requirements.

However, obstructions to light propagation - internal (impurities, bubbles) or external (dust and/or dirt) will cause light scatter same as with a reflective coating.

◄ 4.8.7. Offner null test    ▐    5. INDUCED ABERRATIONS ►

Home  |  Comments