13.5. Higher order monochromatic eye aberrations

Though there is no limit to the number of higher-order terms in the Zernike expansion, terms of some significance limit to the 3rd order aberrations - coma and trefoil - and one 4th order aberration - the primary spherical. Other fourth- and higher-order aberrations are still lower, and may have some importance only combined, after larger terms are corrected. Averaged over larger number of individuals, higher-order aberrations gravitate toward zero mean - except spherical, which is consistently biased toward undercorrection (i.e. with significant positive value of the averaged Zernike z4,0 coefficients).

The significance of higher-order aberrations is that they are more hard to correct, or uncorrectable, and may become the limiting factor to eye's imaging quality once the more significant terms like defocus and astigmatism are corrected. This doesn't seem likely, as in the Indiana Aberration Study the residual defocus/astigmatism, corrected to ~0.25D level for all participants, were still significantly higher than the averaged sum of higher-order aberrations. However, it is a possibility on individual level.

Studies are fairly consistent in their measurements of the general level of higher-order eye aberrations, but individual variations are, as with lower order aberrations, rather common and often significant. No single study is representative of the average aberration levels of human eye, but combined they do provide sufficiently accurate and consistent results to outline their range of deviations and approximate magnitude (FIG. 228).

Despite the average higher-order aberrations lowering optical quality of the eye below diffraction limited level already in daylight conditions, and more so with pupil increase in low-light conditions, the consequences for telescope users are near negligible. For aberrations to noticeably affect image quality, sufficient magnification is required, and these are associated with eyepiece exit pupil sizes well below 2mm in diameter, with the level of higher-order eye aberrations drastically reduced (with large apertures, relatively high nominal magnifications are possible with 2-3mm exit pupils, but higher-order eye aberrations remain negligible in comparison with the seeing error).

Follows more detailed account of the three most significant higher-order aberration of the eye: primary (3rd order) coma, trefoil and primary (4th order) spherical aberration.

Primary coma

A third-order aberration in ophthalmology, primary coma is associated with Zernike terms Z and Z (vertical and horizontal coma, respectively), and corresponding Zernike (expansion) coefficients z3,-1 and z3,1 (in the single-index notation, Z7, Z8, and z7, z8, respectively). Like astigmatism, coma in human eye is often present on axis as well.

This axial coma results from the inherent misalignment of main optical components of the eye: both, cornea and eye lens are tilted relative to the visual axis (which is, in effect, chief ray), with the lens also somewhat tilted with respect to cornea, and decentered. Three studies on FIG. 154 give agreeable absolute mean RMS wavefront error values for the axial coma (as a square root of the sum of  z7 and z8 squared) , from nearly 0.17 microns - about 0.3 waves in units of 0.55μ wavelength - at 6mm pupil, to about 0.11 microns at 5mm pupil (primary coma changes in proportion to the third power of aperture).

Even only a fraction of defocus and astigmatism errors, axial coma at 6mm pupil size in the average eye is still nearly four times above the diffraction-limited level. It should be noted that, since the horizontal term is commonly over 1/2 of the vertical term, axial coma aberration generated by the eye tends to have asymmetric form.

On the average, magnitude of axial coma tend to be roughly comparable to the eye's spherical aberration at larger pupil sizes. Since in passive systems primary coma decreases with the cube of pupil diameter, and spherical aberration with the fourth power of it, coma is generally larger than spherical aberration at smaller pupil sizes; both, however, become negligible.

Axial coma is insignificant compared to axial defocus and astigmatism, but it may vary individually. In general, it increases with age. Also, its relative contribution typically becomes more significant in individuals with very good eyesight, as it tends to linger at similar levels regardless of the overall eye correction. However, its magnitude in such cases is normally low, as well as the magnitude of total aberration.

Off-axis coma generated by the average eye is also small, compared with off-axis astigmatism. Research data is generally scarce, and haven't been in particularly good agreement. However, recent studies provide detailed insight into this subject, and can be regarded as a reliable reference (FIG. 229).

The slope of averaged coma increase with off-axis angle is smallest in young emmetropes (0.006 wave RMS per degree, as the arithmetic average for the two coefficients which, since the two combined determine total coma magnitude, implies 0.0085 wave per degree), and largest in older emmetropes (0.0185 wave RMS arithmetic, and 0.026 wave per degree of off-axis height combined). Note that in the original study (Myopia and peripheral ocular aberrations, Mathur, Atchison and Charman, 2009), there is a discrepancy between graph and printed slope values for the myopes, with the printed values being -0.015 for the horizontal coma coefficient, and 0.014 for the arithmetic average; the above values are corrected according to the graph, but it is uncertain which values are the correct ones.

Off-axis coma of the eye, like other off-axis eye aberrations, has little effect on the quality of telescopic field. However, foveal coma does influence both, quality of the central and off-axis telescopic field. On FIG. 229, the magnitude of coma at the foveal center (approximated as a square root of the sum of positive and negative envelope half-deviations for each coefficient squared), is between 0.06 wave RMS for young emmetropes and 0.08 wave for myopes, with older emmetropes close to the average of about 0.07 wave RMS. This is somewhat lower than in the above two studies, and probably the effect of small sample variations. The actual foveal wavefront is a mix of multiple aberration forms in which, when the largest, 2nd order aberrations are excluded, is dominated by 3rd order coma and trefoil.
 

Trefoil

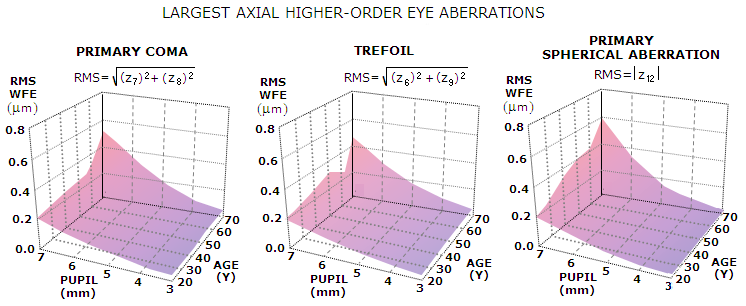
The other third-order aberration, trefoil (or elliptical coma) Zernike term is denoted with Z (vertical) and Z (oblique), and corresponding expansion coefficients with z-3,3 and z3,3 (in the single-index notation, Z6, Z9, and z6, z9, respectively). It is typically close in magnitude (as the power vector form of the two Zernike coefficients, i.e. RMS wavefront error given as the square root of the sum of two coefficients squared) to those of primary coma and spherical aberration. Similarly to them, it can only have some significance at large pupil sizes, after the principal eye aberrations - defocus and astigmatism - are corrected.

Graph below illustrates the magnitude of axial trefoil, as well as those of axial primary coma and spherical aberration, in function of age and pupil size (based on Applegate et al. 2007, 146 normal subjects aged 20-80 years).

In this group, axial trefoil and coma are, as usual, of similar magnitude, while spherical aberration is somewhat higher at large pupil sizes in mid-age and older participant, while lower at smaller pupil sizes, regardless of age. The three increase progressively with pupil diameter and also, at a significantly slower rate, with age. This applies to higher-order aberrations in general, as well as to axial defocus and astigmatism. Of course, individual deviations from the average magnitude of any and all eye aberrations are the rule, rather than exception. They are commonly significant, even within larger groups. For instance, averaged primary coma in a group of 38 normal subjects it was about 50% higher (McLellan et al. 2001).

Off-axis, as its m number indicates, trefoil resulting from surface deformation increases with the third power of field angle. Since its average axial value is not significantly lower than that of 3rd order coma, it would quickly become the dominant field aberration. The field maps from Mathur, Atchison and Charman, however, clearly indicate that this is not the case, implying that the eye trefoil component is mainly caused by misalignment of its optical surfaces - generating relatively even magnitude distribution over the entire field - rather than by surface deformation.

Primary spherical aberration

A fourth-order aberration in ophthalmology, as it is, coincidentally, in the standard optical function, primary spherical aberration is associated with Z Zernike aberration term and z4,0 coefficient (Z12 and z12 in the single index notation, respectively). The extent of this aberration in human eye also varies individually. In general, spherical aberration is minimized by the aspheric (prolate) shape of its optical surfaces, as well as by decreasing refractive index toward the outer zone of eye lens. Unlike the higher-order aberrations in general, its population average doesn't seem to gravitate toward zero mean; instead, the average seems to be significantly into positive value of the Zernike coefficient. In other words, the eye is on average undercorrected.

Also, according to a recent study, spherical aberration is particularly magnified by the increase in eye accommodation; from relaxed state to 5-6D accommodation it increased nearly fourfold (Cheng et al. 2004).

There is a major disagreement in the scientific circles with respect to its average magnitude: direct measurements of longitudinal aberration give about three times larger values than those extracted from wavefront evaluation: for 6mm pupil size, the former gravitate to ~1.5 diopters, and the later to ~0.6D.

Longitudinal spherical aberration Ls is directly related to the corresponding P-V wavefront error at the best focus as Ws=Ls/64F2 which, with the focal ratio F for the eye given by ƒE/P, P being, as before, the effective pupil diameter and ƒE~17mm the effective eye focal length, can be written as

Ws = LsP2/64ƒE2 = LsP2/18,500.

Taking a rough average of 1 diopter between the two above estimates for longitudinal spherical aberration at 6mm pupil size, gives Ls~0.28mm, with the corresponding P-V wavefront error Ws=0.00055mm, or 1 wave for 0.55μ wavelength. Since longitudinal spherical aberration varies with the square of aperture diameter, taking 1D for its rough average at 6mm pupil it can be approximated as Ls~ƒE(P/6)2/60. Substituting in the above relation, with ƒE~17mm, gives a simple approximation for the average P-V wavefront error of spherical aberration:

Ws ~ P4/2,350,000

In units of 0.55μ wavelength, it rounds off to P4/1300. According to it, wavefront error of spherical aberration in the average eye typically varies between 1/1300 and 1 wave P-V at 1mm and 6mm pupil, respectively. With the RMS wavefront error for primary spherical aberration smaller than P-V by a factor of 1/√11.25, the approximate error in terms of RMS deviation is ω~P4/7,880,000 or P4/4334 in units of 0.55μ wavelength. Substituting diffraction limited ω=1/√180 gives the diffraction limited pupil diameter in terms of average spherical aberration error alone as P~3230.25=4.2mm. At 3mm pupil diameter, the error is already 1/4 of the diffraction-limited level, thus entirely negligible.

Again, it may be only a rough average, not only because of disagreements in experimental measurements, but also due to eye's varying levels of adjustment. However, it seems safe to conclude that spherical aberration of the eye is unlikely to be significant factor in observing with a telescope. It may be relatively significant at large pupil sizes, but it is inconsequential, for two reasons: it is still significantly lower than other axial aberrations of the eye, and low magnifications associated with large (eyepiece) pupils are insufficient to make its effect on image quality perceptible.

Unlike telescopes, where primary spherical aberration does not vary with field radius, its variations over eye's visual field are significant relative to its overall magnitude (FIG. 231). It is caused by random local deviations in radius, asphericity and refractive power of eye's surfaces and media.

Like with coma, and other off-axis eye aberrations, the magnitude of off-axis spherical aberration or, for that matter, of higher-order aberrations combined, is of little significance for the quality of telescopic field. Due to eye movements directing it toward selected point, it is mainly axial eye aberrations that combine with telescope (including eyepiece) aberrations.
 

◄ 13.4.2.  2nd order defocus and astigmatism, off-axis   ▐    13.6. Eye chromatism ►

Home  |  Comments