|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
8.4.2. Two-mirror TCT
▐
8.4.4. Off-axis Newtonian
► 8.4.3. Two-mirror tilted component telescopes 2
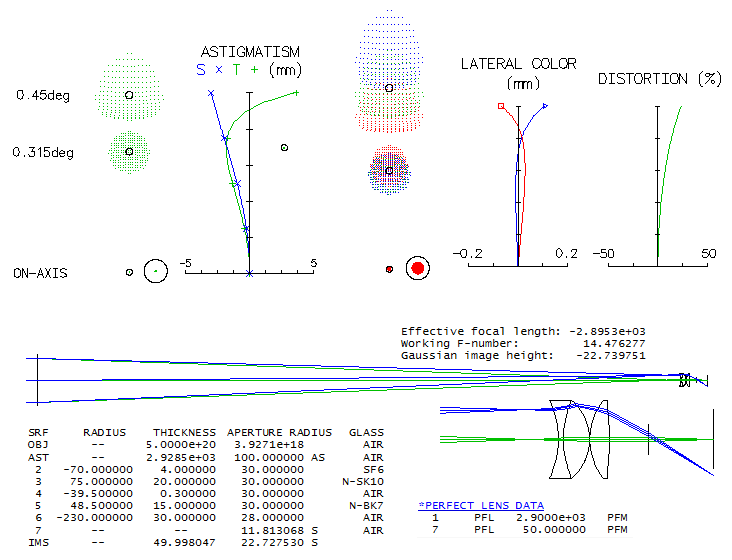
PAGE HIGHLIGHTS In the course of years, arrangements with three and four mirrors are added, in various combinations of surfaces. While adding more mirrors does not necessarily improve performance significantly, it is generally easier to correct aberrations in a system with more surfaces. Few of those systems can achieve satisfactory performance at focal ratios closer to f/10, most of them being still in the f/15 to f/25 range. More elements, however, means more difficult alignment which, in practical terms, can take away most of the performance enhancement. Further reduction of aberrations, allowing for faster focal ratios and more compact instruments, can be also achieved using a multiple-lens corrector. The best example of this type of tilted-element telescopes is catadioptric schiefspiegler designed by Ed Jones (Jones' Chief). It uses a pair of tilted PCX and PCV lenses with a single paraboloidal mirror to practically correct the astigmatism - on and off axis - down to f/7, and even faster. Remaining aberrations are visually near negligible off-axis coma and lateral color. As the system below shows, the lenses are placed close (minimizes lateral color) in an inverse V configuration open toward the incident pencil of light. Combined lens power is weakly positive, resulting in f/7.7 system with f/7.9 mirror. For given pair of lenses corrected for longitudinal chromatism, axial astigmatism can always be corrected by adjusting lens' tilt. In general, the front lens is tilted counterclockwise (w/lenses above mirror, as shown), and the rear lens clockwise, roughly 50% more than the front lens. Either lens induces both, astigmatism of opposite, and and coma of the same sign (opposite to those of the mirror, as raytrace output at right indicates), but of a different magnitude and in a different proportion. That allows for perfect axial monochromatic correction, as well as minimized (negligible) off-axis astigmatism, with coma remaining the only potentially significant (depending on relative aperture) monochromatic off-axis aberration. Axial lateral color needs to be minimized by slightly decentering the rear lens. However, due to the chief rays passing through lens sections of different power, off-axis lateral color is quite unbalanced, being negligible on one side of the field, but significantly larger on the opposite side (bottom).
For any given lens' location, there is only a single radii pair (within a narrow envelope) that will also correct for axial coma. If stronger, lens will - when optimally aligned to cancel out axial astigmatism - have residual positive (tail up) axial coma, and negative axial coma if weaker. For instance, if both radii in the given system are 10mm stronger, axial coma will vary depending on the particular tilt arrangement of all four elements (that cancels out axial astigmatism) from 0.05 to 0.1 wave RMS. This means that the radii should be within 3mm (3%, or so), in order to keep axial coma acceptable or negligible. However, it only applies if the radius deviation is of the same sign for both lens elements. If, for example, the front lens radius is 3mm longer, and rear lens radius 3mm shorter, axial correction can be still very good (0.011 wave RMS), but off axis astigmatism is nearly 30% larger, and lateral color on the positive field radius more than doubled (on the negative side is already large, hence little affected by this magnitude of change; also, longitudinal color is roughly 50% larger, but the error is still quite small, about 0.05 wave RMS in the F-line). Thus, for staying close to the design field performance, lens radii should stay within 2%, or so, of the design. Also mirror tilt and radius need to be close to the design values. Increasing mirror tilt 0.1 results in 0.06 wave RMS of axial coma and about 50% greater off-axis astigmatism. Tilt smaller by the same amount results in nearly 0.04 wave RMS of negative axial coma (off axis astigmatism doesn't change appreciably, but it becomes imbalanced, increasing roughly 50% on one half of the field, while nearly reducing to zero on the other). Mirror radius 2% longer would require about 13.5mm increase in the mirror-to-front-lens separation, with the residual axial coma of little over 0.02 wave RMS requiring in addition about 2/3 of a 10th of a degree mirror tilt reduction, and a slight adjustment of the tilt of either front or rear lens (0.08° less and 0.2° more, respectively). With only lens separation adjustment, axial coma is acceptable (Strehl better than 0.95) up to about 3% mirror radius deviation. Placing lenses closer to the focal plane does not significantly change best possible correction of monochromatic aberrations, on and off axis, nor correction of longitudinal chromatism. Lateral color, however, worsens approximately in (inverse) proportion to the reduction in the corrector-to-focus distance (shown on the bottom for the corrector 100mm farther away from mirror), due to the stronger lenses required for correction of monochromatic aberrations. Other unusually fast TCT arrangements are possible, but they are generally more complex and/or bulky. In addition, they commonly require more strict tolerances in spacing, centering and tilt angles than a comparable axial Newtonian. This is the practical negative of this type of system, since imperfect collimation error can more easily make the difference between high and mediocre - or worse - optical quality in actual use. On the other hand, both the primary and the lens pair in the Jones catadioptric schiefspiegler, for instance, are significantly less sensitive to miscollimation than secondary mirror in the Ritchey-Chretien of comparable aperture and f-ratio.
Reducing the
aperture size allows for larger TCT relative apertures, but there is not much
room in that direction, since they are already relatively small. An interesting compact solution is given by
Herrig's two-mirror
4-reflection system. As the system below shows, both mirrors are
oversized, but their separation is significantly
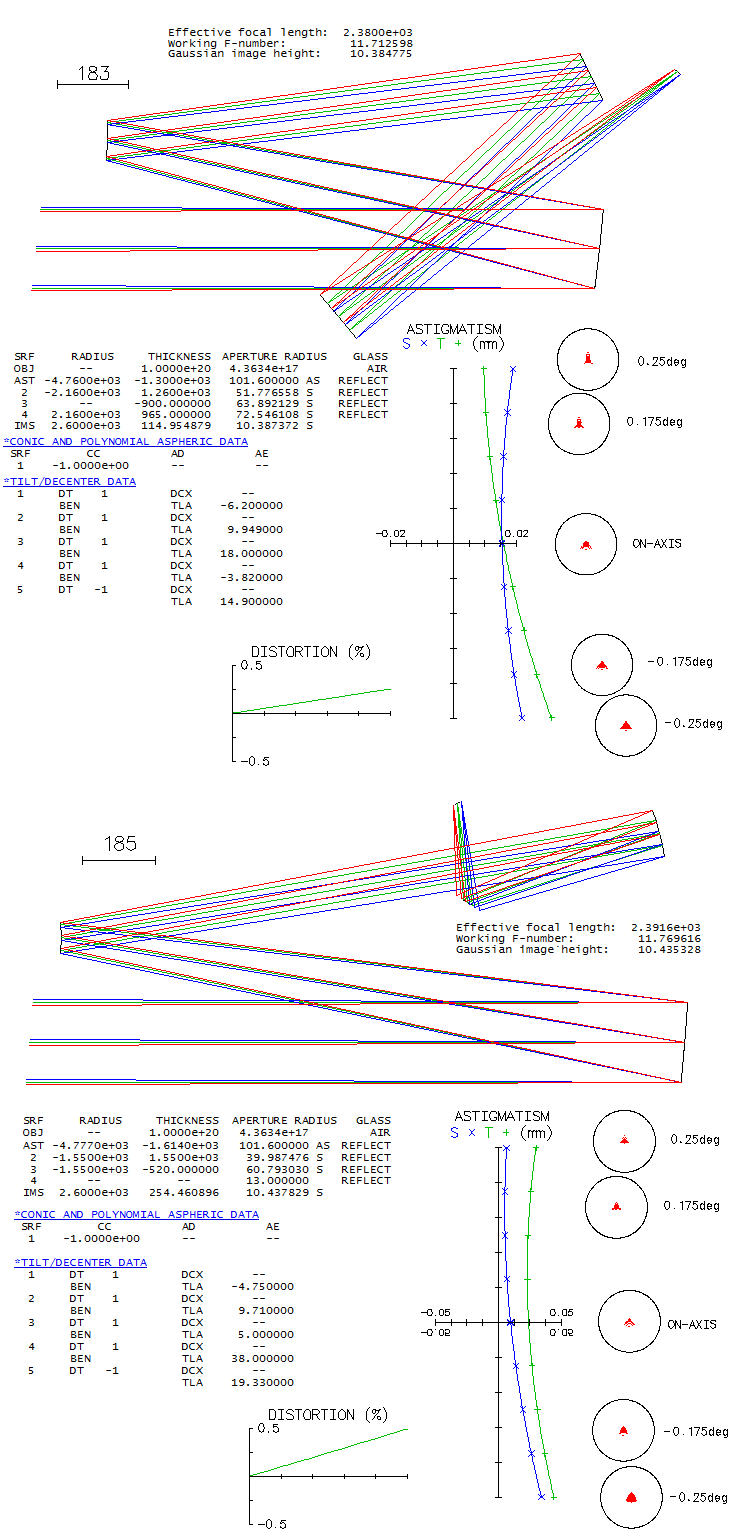
Dominant axial aberration is spherical, mostly coming from the secondary/quaternary (which is somewhat offset by that from the primary/secondary). Secondary to it is trefoil, creating triangular pattern within the ray spot. Since spherical aberration changes with the 3rd power of focal ratio, relatively small changes in the power of two mirrors can have appreciable effect on its axial correction level. Farther off axis, it is astigmatism and coma that dominate (noting that the change in astigmatism, being a sum of the two mirrors' contributions opposite in sign and roughly comparable in magnitude is, for practical field sizes, closer to linear than quadratic vs. field angle). The magnitude of off-axis aberration is also very sensitive to the system focal ratio (i.e. to mirror radii). For instance, making the top system f/16 cuts off axis aberrations nearly in half, and to less than half on axis. Similar change, only in the direction of error increase, would result from making the system faster. The second system (middle) illustrates the mechanics of Herrig's arrangement. Decrease in tilt of the first mirror requires compensatory decrease in the second mirror relative to the first, in order to keep their combined off axis aberrations at a minimum. As a result, tertiary reflection on the first mirror is drawn closer to the first reflection, thus smaller mirror diameter is needed. However, lower part of the first mirror now throws 4th reflection onto the second mirror higher, separating 4th and 2nd reflection wider, thus requiring larger second mirror. The imaging cone is noticeably shorter, but the system focal ratio is only slightly faster, and the level of correction is nearly identical. The mirror radii here are somewhat different, because they were used to correct for the residual axial astigmatism and coma, resulting from the change in tilt of the first mirror. Changing the radius of either mirror alone can correct for the astigmatism, but correcting the coma too requires change in both radii, in a different proportion. Mirror separation is also a bit larger, which helped reduce the positive (tail up) axial coma residual (it also reduces off axis coma to a similar degree). For a given set of mirrors, however, switching from - in this example - 9° to 8° first mirror tilt requires an increase in mirror separation in order to correct for the residual axial coma, and adjustment of the second mirror tilt to correct for axial astigmatism (bottom; this system is given in a 3-D projection, also showing the individual reflections). The resulting system is only slightly slower, but the imaging cone is somewhat shorter. First mirror is slightly smaller, and the second slightly larger than with 9° first mirror tilt. The second mirror is closer to the incoming beam of light, but there is still room left for another half a degree, or so, of the first mirror tilt reduction. That, however, would not produce appreciable change in the correction level, nor a gain in system compactness. Since each surface tilt is relative to the previous surface, the effective image tilt vs. optical axis is a sum of all tilt values. It is 5.97°, 5.34° and 5° from top to bottom, respectively. It should be noted that since OSLO (at least in the free edition) does not allow return to a previous surface, this system has to be constructed by bringing the two reflections on each mirror - each shown as a separate surface on the system drawing - to overlap in their cross sections as closely as it can be visually perceived. Since they are spheres of the same radius, when their central cross sections coincide, they are a part of the same, larger sphere of the same radius. While they are not perfectly in it, the error is generally negligible. Related to this, miscollimation sensitivity for tilt error is about three times larger with the second than first mirror; 0.1° tilt error with the former induces about 0.9 wave P-V (0.2 wave RMS) of mostly astigmatism, nearly evenly across the field (slight residual coma shifts into field center, with the coma-free spot moves off center approximately by the tilt error doubled). As RMS wavefront error, it is slightly more than sensitivity to misalignment of a 200 f/5 paraboloid. Decenter of the second mirror results in about 0.025 wave RMS of mostly astigmatism per 1mm, also nearly evenly across the field. At the end, two more complex TCT systems that, while not two-mirror TCTs, deserve mention for different reasons: one for its unique potential to combine with well corrected small telescopes to expand their effective aperture, and the other for its practically perfect correction. An arrangement well known and used in the professional astronomy is afocal off-axis arrangement with two confocal paraboloids. Hereafter it will be referred to as off-axis Mersenne. The two paraboloids are a beam reducer, with the secondary off-axis section being smaller than the primary. But for a telescope placed in the collimated beam produced by the secondary, it is practically an aperture expander. While most any type of telescope objective could be used for the imaging element, unobstructed one is needed for an overall unobstructed system. System below uses such aperture expander to turn a 67mm apo doublet into 200mm aperture. For clarity, very fast paraboloids are used (f/1.25 for the full aperture; for amateurs, the limit to fabrication is about f/2.5). The reduced collimated beam is free from spherical aberration, coma and astigmatism regardless of the focal ratio of paraboloids. No image tilt, and the only aberration is Petzval field curvature by the secondary (which is only partly offset by that of the primary).
The price to pay for the expanded aperture is lower field quality with respect to the imaging telescope alone, due to the larger off axis angles of rays coming off secondary. Still, correction is good, (much) better than with the obstructed Mersenne, due to the lower off-axis angle magnification factor on this, weaker secondary. Field remains nearly identical if a conventional apo triplet is used, but gets significantly better - as it does with the obstructed Merssenne - if the imager is a Petzval apo. In this example the effective aperture of the doublet is 67mm, with the approximate (from the lens-to-focus separation) f/10.7 focal ratio. The Petzval (and the entire system with it) is about f/8.5. For more realistic paraboloids' ratios (f/2.5-3 parent mirrors), a small very-long-focus achromat can also be used. Inset bottom right shows field of such a system using 50mm f/24 achromat to create, in effect a 200mm f/24 (the Airy disc and spots are reduced by a factor of 2, except for the F-e-C spot top left). The field is smaller angularly for given linear size, but correction doesn't worsen significantly to the very edge. The farther off spectral lines are still bloated, but they matter little for visual observing (photopic polychromatic Strehl is about 0.96, in the "true apo" area). And a design that surpasses all other tilted mirror telescopes in regard to image quality is the Stevick-Paul three-mirror system (FIG. 135), the off-axis cousin of the Paul-Baker telescope invented by Dave Stevick. It is the only TCT anastigmatic aplanat in the f/10-f/12 relative aperture range, with only a mild field curvature remaining. However, the final image is strongly tilted with respect to optical axis.
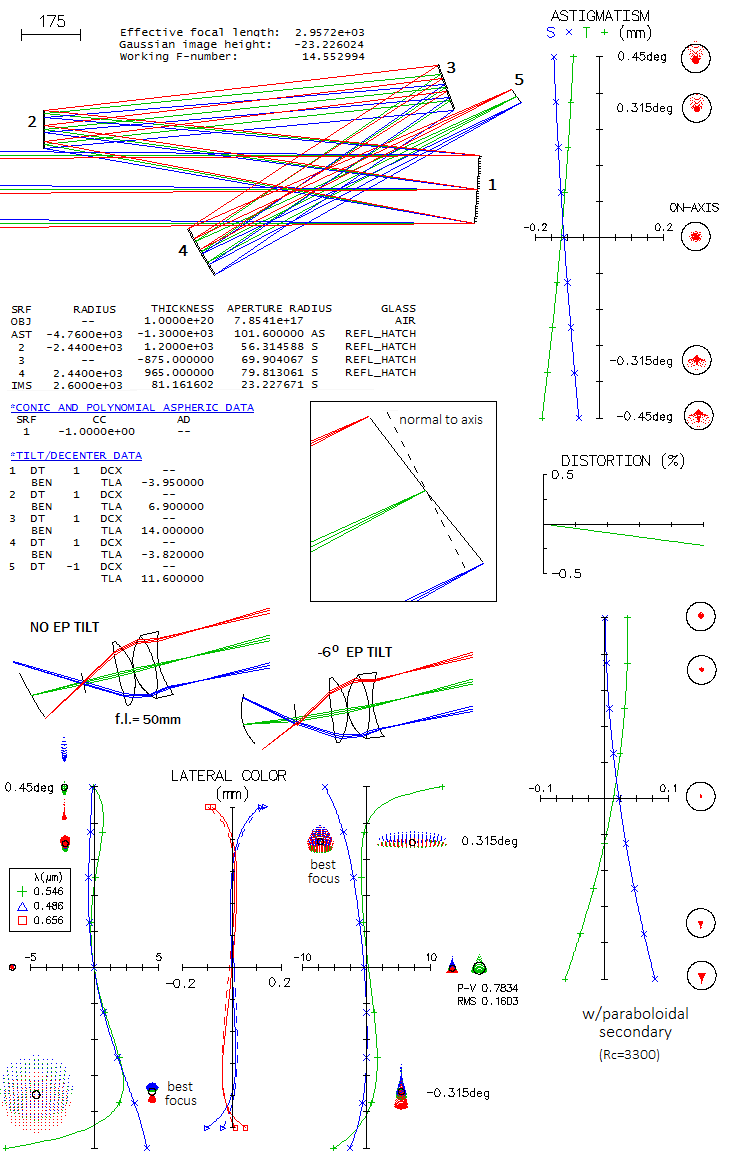
FIGURE 135:
Stevick-Paul 3-mirror TCT bases its exceptional performance
on the freedom from off-axis aberrations of a sphere with the stop at
the center of curvature. The convex secondary sphere (2) is confocal with
the paraboloidal primary (1), producing collimated beam and acting as an
aperture stop for the concave spherical tertiary (3). Having identical radii of
curvature, secondary and tertiary cancel each other's spherical
aberration. A small flat (4) makes the final image accessible. The ray
spot plot is for an 8" f/11.7
system (based on design from WinSpot, graphics generated by
OSLO). Image quality is practically perfect across the best
image surface, which has 2250mm radius (since astigmatism is
practically non existent - tangential and sagittal surfaces are
slightly separated and nearly concentric - and the two mirrors
with identical radii cancel each other's Petzval out, image
curvature results from the primary's Petzval curvature radius
(equal to the primary's focal length, concave toward eyepiece),
and is well approximated by it (the curvature will cause
asymmetric field on the two opposite sides in the direction of
tube axis, if the image tilt - in this case 8.97°
with the end toward tube
front lower - is not compensated for. On flat field, the system
is better than diffraction limited as far as 21mm off axis. As
plot bottom left shows, distortion is also very low. To make larger field possible, mirror tilt has to increase, and with it increase the aberrations as well. It can be partly countered by making mirrors slower, but it makes already bulky configuration bulkier. One interesting posibility is to fold the secondary-to-tertiary path by inserting flat between them, as shown below (increasing tilt angle of the flat makes the final beam come out at a larger angle, but tertiary falls farther down from the incoming light). Possible field is now up to one degree in diameter, but the question is how well corrected is that field.
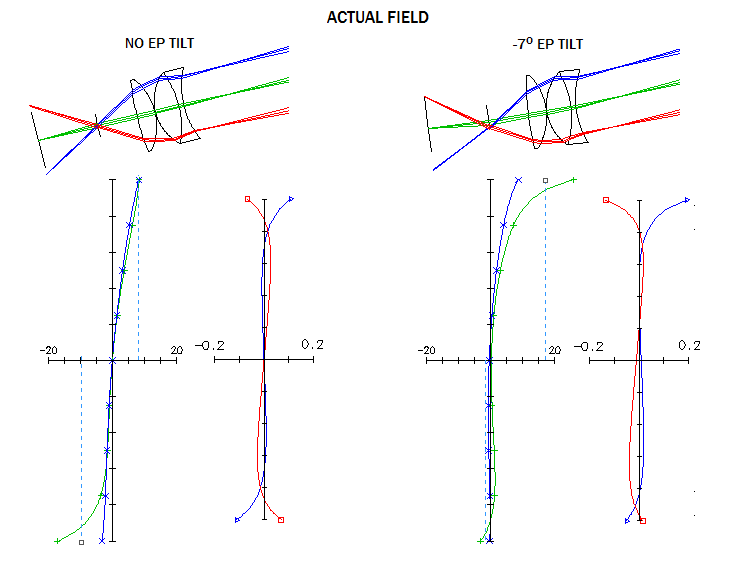
The primary has nearly identical focal length as in the first example, and the secondary and tertiary are significantly more relaxed. Astigmatism is still very low, and there is negligible trace of off-axis coma (top right). If the secondary is also parabolized, correction level is closer to that in the first example (bottom right; slight correction in tilt of the secondary or tertiary would eliminate center field astigmatism - already entirely negligible - and make the two side of the astigmatic field more balanced). Main reason for the higher level of residual aberrations of this system is broken symmetry of the Paul-Stevick: in order to keep three mirrors as tight together latteraly as possible, primary tilt is less than what is required for corrected coma, which has to be compensated by placing secondary somewhat farther away from its confocal position. As a result, the beam reflected from it is not collimated, but midely converging, causing imbalance in spherical aberration on the 2nd and 3rd mirror, some residual coma, and slower focal ratio. Also, due to the limitations imposed by configuration, image tilt is 11.6° and the question is how it will affect eyepiece image. Since the image plane is not perpendicular to the optical axis, eyepiece cannot be aligned with both at the same time, and it will affect properties of its astigmatic field. Raytrace shows that it causes very unbalanced astigmatic field, with astigmatism on the top field edge much smaller than on the bottom, with lateral color error also being asymmetrical (bottom left). Note that the field radius sign is unchanged from the objective's image despite the blue (negative) cone crossing over above the axis after refraction through the eyepiece (the orientation of the final image is reversed and directional angle smaller because the raytrace with eyepiece omits the flat, in order to fit into 10-surface OSLO Edu limit). Exit pupil becomes incoherent, with the marginal cones narrower, and shifted laterally vs. axial cone. That doesn't affect "perfect lens", but would affect the output of human eye. Tilting eyepiece (50mm f.l. Koenig) somewhat more than one half of the image tilt reverses configuration of the astigmatic field, with no appreciable change in the lateral color error (dashed). Distortion is significant (up to ~25%) and unusual, being barell toward field top and pincushion toward bottom (kind and magnitude of distortion are indicated with the mismatch between the image surface, which represents undistorted, Gaussian image, and tip of the marginal cone, which determines the actual - apparent - image size). The 0.45° blur is too big to fit in the picture, but the given 0.7 field blur indicates its size (for points not in the central plane both flat field - i.e. zero accommodation - and best focus blur are shown). Note that both astigmatic fields are given vs. roughly best field curvature - 330mm left and 44mm right - to bring out the astigmatic field more clearly. For the same reason, image field is tilted 17° and 6°, in the same order (make sure not to confuse the final image tilt and the eyepiece tilt). Required accommodation is within one diopter w/o eyepiece tilt, for bottom half with -7° tilt (-6° in the image is error); it is nearly five diopters for the top half edge, falling to 1.2 diopter at the 0.7 zone. Most importantly, there is a prohibitively large center-field astigmatism. Fully aligning eyepiece with image plane (-11.6° eyepiece tilt) results in over 2 waves P-V of center-field astigmatism and more field astigmatism. Decentering eyepiece by about 1mm has a small overall beneficial effect if positive (moving up) and more astigmatism if negative. At 2mm positive decenter the two sides of the field are roughly balanced, but the center-field astigmatism is nearly 1 wave P-V. Taking out field curvature adjustment in the plot at left still leaves the field within ±1 diopter. However, taking out the image tilt results in edge accommodation of 4 (bottom) and -3.2 diopters (top) required, dropping to -1.2 and 2 diopers at the 0.7 zone, respectively (below). Lateral color and distortion are nearly identical on both sides.
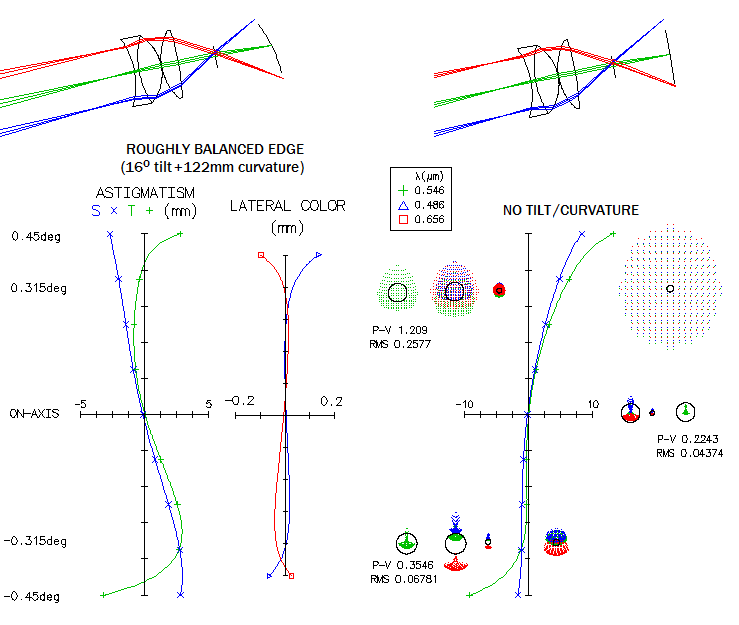
With the plot at right, without tilt and field curvature - i.e. with the actual image field - required edge accomodation increases to nearly -7 diopters on the field top, while being a fraction of diopter on the bottom. Since these images are projected onto retina, it is not possible to improve on them. Overall, image with untilted eyepiece, i.e. aligned with optical axis, is better. Eyepiece tilt resulting in roughly balanced astigmatic field and distortion along vertical diameter is about 3.5° in the direction of image tilt. Image below shows that it still suffers from both excessive off axis astigmatism and lateral color error. Astigmatic field at left is again vs. curved surface (122mm), 16° tilted to roughly balance the top and bottom edge blur. Without these, edge astigmatism is balanced in magnitude, but the two sides of the field have very different orientation vs. central plane (left).
Even the field at left has most of it more or less defocused. Since one diopter of accommodation here is 2.5mm (f2/1000), defocus is within one diopter (infinity to 1m accommodation) i.e. easy for most people (note that diopter of accommodation changes with the square of eyepiece f.l. while the linear field diameter changes in proportion to it; so a 10mm f.l. unit with this same image would have the maximum accommodation requirement close to 5 diopters). However, what the eye has to deal with is unajusted field (right). Blurs on the right are for flat field (zero accommodation), and on the left for best focus; the latter are also given magnified. The top 0.7 field has significant astigmatism, the bottom is better than "diffraction limited". Required field edge accommodation is 4 diopters for the top field edge, half as much for the bottom, and the 0.7 top zone. Bottom half of the field is easily focusable, but the top is not toward the edge, and more toward inside with shorter f.l. eyepieces. Increased accommodation requirement with shorter f.l. eyepiece is well illustrated with off-axis Newtonian. Astigmatic field also can be roughly balanced by decentering eyepiece. With no eyepiece tilt, needed decenter to roughly balance the field is about 3mm lower. The field still has substantial tilt, with the edge field accommodation over two diopters positive for the top, and nearly three diopters negative for the field bottom (again, for 50mm f.l. eyepiece; for 10mm f.l unit would have been about five times larger, i.e. beyond accommodation capability of the eye, unless the eyepiece is tilted).
Latteral color is grossly unbalanced toward the edge, and unacceptable already at 0.7 field zone. Distortion is negligible toward field top, and huge toward the bottom. In all, worse than without eyepiece tilt alone. It is possible that a combination of tilt and decenter would produce best field correction, but seems there is no way to achieve near complete correction. If, for instance, this decenter is combined with -6° tilt, top portion of the field becomes nearly flat, with acceptable correction of astigmatism and lateral color, but the opposite side develops strong tilt, as well as severe astigmatism and lateral color from 0.7 zone up. This is because the change in tangential astigmatism that brings the top side closer to flat, at the same time causes the bottom side to becomes more tilted and astigmatic. In order to separate eyepiece aberrations from those induced by image tilt and mirrors, it is necessary to raytrace eyepiece with its inherent aberrations only. Image below shows 200mm f/14.5 perfect system with the same 50mm f.l. Koenig on flat field (objective and eye are OSLO "perfect lens"; eye lens not coinciding with the exit pupil does not induce aberrations). It is obvious that edge astigmatism, lateral color and distortion (indicated by the mismatch between the end of image surface point and the tip of the marginal beam) are produced mainly by the eyepiece, and the consequence of tilt is mainly imbalance between top and bottom of the field, although tilted image does show significantly more of field astigmatism on one side as well (0.7 zone monochromati ray spot plot at right of the astigmatic plot is the best focus spot for that field radius). For this particular Koenig design, true field should be about 20% smaller (since eyepiece magnification is x58, and pincushion distortion makes the apparent image 25% larger, the 0.45° true field radius - corresponding to the image surface shown by raytrace (Gaussian image) - transfers into 32.6° apparent field radius through the eyepiece).
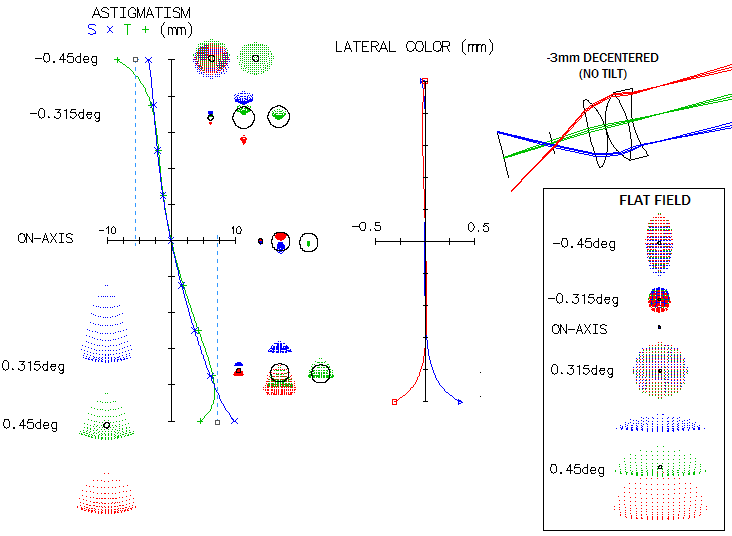
Overall picture indicates that the maximum quality field is about 0.7 the field diameter, or 0.3° field radius, which would also allow for decreased mirror tilt and yet better correction. Eyepiece tilt resulting in roughly balanced astigmatic field is only a fraction of the image tilt. The fact that its astigmatism is unbalanced with either eyepiece alignment - vs. optical axis or image plane - indicates that unbalanced astigmatism is the consequence of skewed geometry, and that it would be induced even if eyepiece itself wouldn't generate astigmatism. Tilting eyepiece doesn't make the actual image on the retina better with respect to astigmatism - other than making it roughly balanced across the field diameter if correct - but does induce asymetries, possibly excessive, with respect to lateral color error and distortion. Correct amount of eyepiece tilt roughly balancing astigmatism is a fraction of image tilt, and likely varies with eyepiece properties. For comparison, below is shown such system (mirror-mirror-flat-mirror, or MMFM) with preserved symmetry. It is better corrected - which is of no practical significance - but it is over 20% wider laterally. As a consequence of more strongly tilted mirrors, image tilt is also stronger, at 14.9°. With a compact MMMF arrangement (bottom), also preserving system symmetry, lateral width is nearly 20% smaller, but length is 26% larger. More importantly, image tilt is as much as 19.3° (both systems have a slightly stronger image tilt, and field curvature than those used in raytracing, but it is entirely inconsequential).
To give some idea of the collimation tolerances, misalignment causing the last system to drop near "diffraction limited" (0.80 Strehl) level on axis is approx. 0.03° (1/20mm at the edge) tilt of the primary, or 0.05° tilt alone/1.2mm decenter alone on the secondary, or 0.09° tilt alone /2.3mm decenter alone on the tertiary. Dominant induced aberration is astigmatism, with little or no coma. Despace error in this context is 15mm between primary and secondary, and no practical effect of despace error between secondary and tertiary, except that larger separation increases image tilt, and smaller separation decreases (in this particular case, reducing the separation by 50mm decreases image tilt by 1/3 degree, with a negligibly small increase in off axis aberrations, mainly astigmatism). Despite some of these systems being very well corrected, obstruction-free and relatively insensitive to miscollimation, they never became really popular, even in the small-aperture range. Telescopes of this kind are usually built by amateur enthusiasts. Among the reasons are probably their odd appearance, relatively complicated element positioning and bulkiness of the tube assembly. A system somewhat less affected by these drawbacks is the off-axis Newtonian (other off-axis configurations are possible, but even less price-competitive).
|