|
telescopeѲptics.net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ CONTENTS
◄
8.4.1. Herschelian
▐
8.4.3. TCT 2
► 8.4.2. Two-mirror tilted component telescopes
PAGE HIGHLIGHTS By replacing the flat in a Herschelian with a toroid, in the same configuration, or with a second curved mirror directing light back toward primary, needed mirror separation can be reduced roughly two two three times, for a similar level of correction. Field asymmetry is also reduced. Best known systems of this type of tilted component telescopes (TCT) are the variants Schiefspiegler and Yolo. The former is introduced by S.A. Leonard in the early 1960s. It uses two concave mirrors, one of them toroidal (a sphere deformed into a toroid by a specially designed cell). In general, it achieves better - and exceptionally good - performance than the Schiefspiegler (Schief for short), and the systems can be considerably faster. On the other hand, it is also more complex. The Schief is created by Anton Cutter, and originally uses a pair of spherical mirrors, the secondary being convex. The aberration here is present in the field center, and has to be kept acceptably low by limiting a system to quite small relative apertures, typically ~f/20 and smaller.
Aberrations of a tilted-mirror system are a sum of the aberrations at each mirror. The principles of aberration compensation can be outlined using the basic two-mirror arrangement. Here, aberrations at the primary are simply off-axis aberrations for the field angle equal to a mirror tilt angle τ1, typically ~3°, and possibly residual spherical aberration to compensate for that induced by the secondary (not needed in traditional TCT arrangements, due to mild surface curvatures). For the secondary, the object is the image projected by the primary. Since the secondary is centered around the reflected axis of the primary (i.e. around the chief ray of the axial cone), its aperture stop coincides with its surface for the center-field aberrations, not only for spherical aberration, but also for center-field astigmatism and coma. For other field points, the chief ray height at the secondary differs from zero, and the aperture stop is shifted to the primary. These features make two-mirror TCT alike axial two-mirror systems in one, and different in another respect. The similarity extends to secondary magnification and spherical aberration, for which the same general two-mirror system relations (Eq. 78 and Eq. 80, respectively) apply to TCT's as well, including center-field astigmatism and coma, formally abaxial aberrations. For TCT's abaxial aberrations outside the field center, regular stop-shift relations for abaxial aberrations of the two-mirror system secondary apply. This means that for astigmatism wavefront error, which doesn't change with object distance, and for coma, which changes with object distance, the aberration relations that apply for the secondary mirror contribution in the field center are Eq. 19, and Eq. 15, respectively. For all other field points, astigmatism and coma at the secondary are calculated either from general two-mirror system relations (Eq. 82-82.1), or from Eq. 15.2-15.3 and Eq. 19.1 and Eq. 22 for coma and astigmatism, respectively. The consequence of TCT mirror tilt is that it places off-axis aberrations in the field center by effectively moving the field far off-axis - with individual aberration contributions of the primary and secondary being determined by their tilt angles. The primary mirror field is a circle far off from the optical axis (left on the above illustration), with strong astigmatism and coma at the same level along the field cross-radius centered at the optical axis (the field center for axially oriented mirror). Along the central field meridian orthogonal to this radius, coma and astigmatism increase according to the angle measured from the optical axis. In between, there is a gradual transition from one form of aberrated field to another. Actual TCT field radius is typically only a fraction of the tilt angle at the primary. TCT's primary mirror center field astigmatism and coma, commonly at the level of 10 and 2-3 waves P-V, or higher (respectively) are, for best focus location, given by:
Wa1=-D1(τ1+α)2/8F
and
Wc1=(τ1+α)D1/48F2
respectively, with D1 being the aperture
diameter, α
the angular differential, in radians, between the tilt angle τ1
and the angle determined by the point distance from the optical axis
(for the tangential - vertical - field meridian, it corresponds to field angle relative to the field center), and
F the focal ratio of the primary.
The main goal of the two-mirror TCT's
secondary is to minimize
this center-field aberration induced by tilted primary. This is
accomplished by tilting it to induce offsetting aberrations,
with the secondary mirror tilt angle τ2
measured with respect to the axial ray reflected from the primary (i.e.
the chief ray for axial cone).
Center-field astigmatism and coma at the secondary, also as the P-V wavefront error
at the best focus location, are given by:
Wa2 = -τ22D22/4R2
respectively,
with R2,
D2,
τ2
being the secondary radius of curvature, effective aperture diameter
(i.e. the minimum secondary size) and tilt angle, respectively,
α being the
field angle as defined earlier, and Ω=R2/l
the inverse of relative object distance for the secondary
l (secondary to projected focus of
the primary separation) in
units of the secondary radius of curvature. Since both, R2
and l are, according to the
sign convention,
numerically negative, the sign of Ω is positive.
Note that
only a convex secondary, with numerically negative radius of curvature, offsets astigmatism
and coma generated by tilted primary.
For the field points outside the center, astigmatism and coma at the secondary,
as the P-V error at the best focus location, are given
by:
with
σ being the secondary to the
aperture stop (i.e. primary) separation in units of secondary's radius
of curvature, numerically negative for convex secondary (note that these relations are valid
for two-mirror system secondary in general, with the tilt angle
τ=0 for axial systems). The field angle
α, as mentioned
before, is the angular differential between the tilt angle of the
secondary to the reflected optical axis of the primary and field point
angle measured from the point to the reflected primary's axis.
Numerically, it can be either positive or negative (zero for the field
center).
With coma and astigmatism being in different proportions throughout the
field of the two mirrors, due to their different tilt angles (that of
the secondary is commonly in excess of double the primary's tilt angle), the final image in
a simple TCT, after the center-field aberration is minimized, has only partially corrected field - unless of
very small relative aperture - with uneven distribution of off-axis
aberrations. Uneven compensation of astigmatism can, and most often does induce image tilt. Even
the very field center is a compromise: since it is impossible to
generate with the secondary's tilt the exact proportion of astigmatism and
coma that are induced by primary's tilt, some level of residual aberration
remains present.
These consequences of the uneven aberration match of two different far off-axis field
segments limit simple two-mirror TCTs - and most more complex tilted
systems as well -
to small relative apertures and smallish aperture diameters.
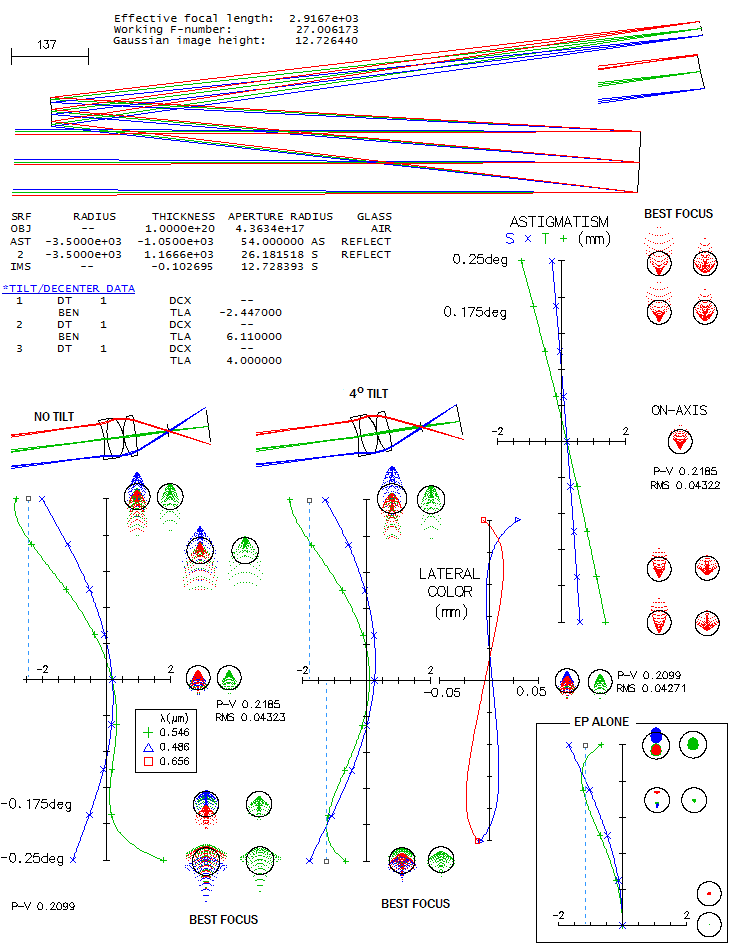
EXAMPLE: Anton Kutter's 110mm
f/24.7 schiefspiegler, with concave
f/14.7 spherical primary and spherical convex secondary,
with the primary-to-secondary separation of 965mm. Radii
of curvature R1=R2=-3240mm, secondary to primary's
projected focus distance l=-655mm,
the inverse of relative object distance for the secondary
Ω=R2/l=4.95, secondary mirror effective diameter D2=44.5mm,
and the tilt angles τ1=2.65°
and τ2=6.65°
for the primary and secondary mirror, respectively. Best image field is
astigmatic but flat.
In the field center (α=0), primary
mirror astigmatism and coma contribution is
Wa1=-0.00193mm
(3.5 waves P-V, in 550nm wavelength units), and
Wc1=0.00048mm
(0.9 waves P-V), respectively. With the secondary mirror contributions of
Wa2=0.00198mm
and Wc2=-0.00032mm,
the system aberrations are
WaS=Wa1+Wc1=0.00005mm,
or 0.09 wave P-V of Seidel astigmatism (higher-order is entirely
insignificant), and
WcS=Wc1+Wc2=0.00016mm,
or 0.29 wave P-V of coma. This is close to 0.27 wave P-V output by the
exact ray trace (OSLO) for the final center field aberration (relatively
low astigmatic deformation has little effect on the P-V error of coma).
The vertical secondary radius is now -3,186mm, and image
tilt is now 6.5°. Obviously, this arrangement would allow for
significantly faster systems.
Coma could be also diminished with the reduction in
the primary (and secondary) tilt angles, but that would cause secondary
intruding into the light falling onto the primary (at 1.6° primary
tilt, the center field RMS drops to 0.032 wave, but the
secondary is halfway into the axial pencil of light falling onto the
primary). Better option is to increase secondary tilt to correct
coma, and add a third mirror to take care of astigmatism, which
leads a system like Terry Platt's Buchroeder.
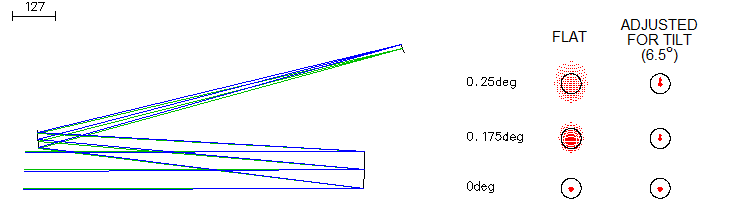
The ray spot plots illustrate the field match in this two-mirror TCT
system. Secondary's field is farther away from its axis, thus its ray
spots have larger proportion of astigmatism, lower degree of
variation in the size of aberrations across the field's vertical
diameter, and less of the angular spot inclination toward the ends
of field along the diameter orthogonal to it. These differences between
the two combining field result in the final seemingly
disarrayed, asymmetrical field (the plot is for the best image surface,
tilted at ~4.5° counterclockwise to the axial ray, as shown in inset top
left).
Another option is to make the secondary
toroid. It allows for
better overall correction of aberrations. The secondary can be either
convex, or concave. The former will, all else equal, result in a slower
system, but it is the system configuration that can also have
significant impact in this respect. In the conventional configuration
(top below), the design minimum in the field center is less than a half
of the minimum error in the comparable catadioptric design, while the
off axis error is roughly cut in half. Making secondary smaller requires
it to have more of a tilt (with the radii kept identical), but will
result in somewhat faster, more compact configuration (bottom below).
The aberration level, both on and off axis, is only slightly higher for
given system focal ratio (note that the toroid is specified under
"surface tag data" as the reverse of the radius value; for instance, in
the 100mm f/24.7 system the secondary radius in the tangential plane -
the one containing axial and chief ray - is -3,240mm, while it is
-3182.3mm in the plane orthogonal to it, with the inverse value of
-0.00031424).
In the arrangement with concave secondary, the
secondary tilt has to have sign opposite to that in the system with
convex secondary, with light reflected from it crossing the incoming
light to focus out on the opposite side of the incoming beam. The first
system of this type, and the best known, is
Yolo by Arthur
Leonard (top below). In it, toroidal form of the secondary is achieved
by placing it into a specially made cell ("warping harness") which folds
it by the action of a tightening nut (top below). The system shown
is Leonard's 12-inch f/15 (slightly tweaked) scaled down to 110mm
aperture. Originally, it has hyperboloidal primary, which also
compensates for spherical aberration of the secondary (which indicates
that secondary here induces roughly three times more spherical
aberration, since it would have been zero if both mirrors were
paraboloids). Raytrace shows that aspherizing does not produce
appreciable gains. Making system faster in this configuration would
increase aberrations approximately in inverse proportion to the focal
ratio. An alternative is to use smaller, more
strongly tilted toroidal secondary (mid/bottom).
The level of aberrations remains similar to the
slower Yolo, mainly due to the less of primary tilt required. The
primary is considerably faster, thus parabolizing it has more of an effect
(secondary's contribution is negligible due to its small size),
but it still doesn't make for appreciable difference: axial blur
nearly the size of the Airy disc implies less than 1/12 wave P-V
wavefront error. There is little difference in correction between
arrangement w/tilted focusing cone (middle) and Newtonian-like
configuration (bottom). While astigmatism can be always corrected, for
any given secondary tilt angle there is only one secondary r.o.c. value
at which this toroidal surface will also correct for axial coma. Off
axis, there is some residual coma but, as wavefront maps show,
astigmatism dominates. Trefoil is still significantly smaller than coma,
thus only noticeable on axis (note that CVX in OSLO prescription stands
for toric curvature, as the reciprocal of the radius value, not
"convex").
These are the traditional two-mirror TCTs.
Some of the most notable more recent developments in this field are
described on the next page.
|
FIGURE 134: The two-mirror TCT final field forms as a combination
of the effective field at each mirror. Since the combining fields are
each a circular off axis area of mirror's field, they are not symmetric
about their respective center points. Since they are likely to have not
only different magnitude of astigmatism, but also different ratio of
coma vs. astigmatism - each changing differently with the field angle -
once the aberration of their combined centerfield point is minimized
with a given combination of tilt angles, aberration distribution over
the field is more or less asymmetrical.
